Đuổi theo các cô gái và tìm tên lửa - Thống kê công thức Bayesian

• ### ONE

Những người chết vì lý trí không hiểu được phong cách của họ trong đời sống cảm xúc chắc chắn sẽ gặp phải một cảnh khóc lóc như vậy: tình cờ gặp một cô gái xinh đẹp, từ đó suy nghĩ, quên ngủ và bắt đầu cuộc hành trình tình yêu bí mật dài, chờ đợi cho đến một ngày, trong những mối quan hệ vô tận, cuối cùng đã dũng cảm để thú nhận với cô gái, kết quả là cô gái nói rằng tôi đã có một người bạn trai vui vẻ như thiên nhiên, thật sự khó chấp nhận …

Để tránh sự lúng túng như vậy, bài học “Làm thế nào để biết một cô gái độc thân” đã trở thành một bài học bắt buộc.

Nếu bạn làm việc cùng một cô gái, thường xuyên ở bên cạnh cô ấy, thì không khó để biết cô ấy có độc thân hay không. Nhưng nhiệm vụ khó khăn mà người theo chủ nghĩa tử thần phải hoàn thành là: là một người lạ giữ khoảng cách với cô gái, có thể sử dụng thông tin hạn chế để xác định tình trạng độc thân của cô gái mà cô gái không nhận ra, không chỉ vậy, kết quả theo đuổi của người theo chủ nghĩa tử thần phải được định lượng, xác suất độc thân được tính toán cũng phải giữ hai chữ số nhỏ.

Bước đầu tiên, hãy tin vào trực giác của bạn. Những người theo chủ nghĩa lý trí có thể cân nhắc tìm thêm một vài người bạn để bí mật quan sát cô gái mục tiêu, tất nhiên những người tìm kiếm không phải là những người theo chủ nghĩa lý trí, nhóm nhận dạng tâm lý, máy nghiền lời đồn, kiểm soát tự nhiên, bác sĩ tư pháp hình sự tốt nhất nên tìm một vài người, người đã kết hôn, người chơi trò chơi, kẻ trộm hoa cũng nên tìm kiếm, càng nhiều càng tốt, càng đa dạng càng tốt.

Những kết quả trên chỉ dựa trên kinh nghiệm và cảm xúc của mỗi cử tri, và những nơi nào trong đó phù hợp với phong cách hành động của chủ nghĩa duy lý khách quan?

Giống như nghiên cứu khoa học, bạn có thể tìm hiểu thông tin trước, tìm kiếm bất cứ điều gì trên google có thể tìm thấy các tiêu chuẩn đơn giản dễ sử dụng mà nhiều người cô đơn đã nghiên cứu trong nhiều năm, chẳng hạn như nguyên tắc điện thoại di động (những cô gái yêu thích sử dụng điện thoại di động thường xuyên hơn), nguyên tắc tự học (những cô gái độc thân thường tự học với một vài cô gái).

Những con số thống kê như vậy.

Khi chúng ta có tất cả các dữ liệu này, chúng ta có thể tiếp tục, sửa đổi và tối ưu hóa giá trị xác suất 65,65% mà chúng ta vừa bỏ phiếu. Dựa vào cái gì? Tất nhiên là hiệu suất của cô gái mục tiêu trên các tiêu chí khác nhau. Ví dụ như phát hiện ra rằng mm mục tiêu thích tập luyện với bạn bè, và dựa trên kết quả nghiên cứu thống kê của mình: trong mm đã yêu, những cô gái thích tập luyện với bạn bè chiếm khoảng 60% trong số đó; trong số những cô gái không có tình yêu, những cô gái thích tập luyện với bạn bè chiếm khoảng 30% trong số đó;

Vì vậy, bây giờ mục tiêu mm là một người độc thân có thể biến thành

Có lẽ trong những bữa tiệc chết chóc, người ta đang vui vẻ, và hy vọng sẽ tăng lên!

Nếu kết quả nghiên cứu cũng phát hiện ra rằng trong số các cô gái độc thân, tỷ lệ sử dụng điện thoại di động cao hơn 1,2 lần/giờ chiếm 20%; trong số những cô gái đã có tình yêu, con số này là 60%.

Lần này, tỷ lệ độc thân đã giảm một cách bi thảm xuống 56.02%, những người chết có lý trí có thể tìm kiếm nhiều tiêu chuẩn đánh giá hơn, làm nhiều nghiên cứu hơn, liên tục cập nhật tỷ lệ độc thân của cô gái, để nó càng gần hơn với sự thật, nhưng trước khi nhận được kết quả cuối cùng, bạn phải đặt một ngưỡng: tỷ lệ độc thân của cô gái vượt quá ngưỡng này (ví dụ 90%), bạn xứng đáng để nhận ra đồng hồ, nếu không, hãy chết đi.

Tuy nhiên, cần lưu ý rằng, bất kể tính toán bao nhiêu lần, kết quả cuối cùng là một giá trị xác suất, không phải là sự thật, ngay cả sau nhiều nghiên cứu, đã có thể xác định xác suất độc thân của cô gái mục tiêu là 99.9%, ngay lập tức sẵn sàng để nói với cô ấy, nhưng trong nghiên cứu quan sát cuối cùng của cô gái, người nhà và một người đàn ông nắm tay nói chuyện cười và ôm nhau, thì xác suất độc thân của cô gái sẽ ngay lập tức giảm từ 99.9% xuống gần 0 …

Phương pháp này được gọi là phương pháp thống kê của Bayes. Phương pháp của Bayes đơn giản là: xác suất tiên đoán + bằng chứng mới = xác suất sau khi sửa đổi. Nó có thể không bị giới hạn bởi lượng thông tin, kết hợp kết quả của các nguồn khác nhau, bao gồm phán đoán chủ quan và thông tin khách quan hạn chế, để đưa ra kết luận cuối cùng.

Tuy nhiên, không thể bỏ qua cái gọi là “luật Bayes” của những người chết vì lý trí, phương pháp mà Hải quân Hoa Kỳ đã sử dụng để tìm kiếm bom hydrogen bị mất, tàu ngầm hạt nhân bị mất tích trên đại dương Thái Bình Dương, và chúng ta sẽ chuyển từ kênh cảm xúc sang kênh lịch sử.

• ### TWO

Vào một ngày tháng 1 năm 1966, một máy bay ném bom B-52 của Mỹ đã bay qua Palomares, Tây Ban Nha, và một số phi công trên máy bay đang thực hiện nhiệm vụ tiếp nhiên liệu trên không do Bộ chỉ huy không quân sắp xếp cho họ. Theo lý thuyết, chuyến bay này không nguy hiểm, người lái là một người rất bình tĩnh, không thích lấy hai ống hút lớn, ngay cả trong buồng bay.

Nhưng câu chuyện vẫn chưa kết thúc, và sau đó là một loạt những bi kịch và hài kịch.

Để tìm kiếm quả bom hạch bị mất, Mỹ đã nhanh chóng huy động một đội ngũ tìm kiếm từ trong nước gồm nhiều chuyên gia đến hiện trường, trong đó có một nhà toán học tên là John Craven, có chức danh là nhà khoa học trưởng của chương trình đặc biệt của Hải quân Hoa Kỳ.

Trong vấn đề tìm kiếm đạn thạch cao, Craven đã đưa ra một đề xuất sử dụng phương pháp Bayes đã đề cập ở trên, ông đã triệu tập các chuyên gia về mọi lĩnh vực, nhưng mỗi chuyên gia đều có lĩnh vực chuyên môn của mình, không phải là tất cả. Một số người biết nhiều về máy bay ném bom B-52, nhưng ít biết về tính chất của đạn thạch cao.

Đối với những câu hỏi khác nhau này, Craven yêu cầu các chuyên gia đưa ra các giả định, tưởng tượng ra các tình huống khác nhau, sau đó phỏng đoán xác suất của đạn thạch cao ở các vị trí khác nhau trong các tình huống khác nhau, và khả năng xuất hiện của mỗi tình huống.

Cách thức của Craven cũng bị các đồng nghiệp đặt câu hỏi, bởi vì trong chương trình của ông, nhiều kết quả được các chuyên gia này đưa ra dưới dạng phỏng đoán, bỏ phiếu hoặc thậm chí có thể nói là cờ bạc, không thể đảm bảo tính chính xác của tất cả các kết quả, nhưng vì nhiệm vụ tìm kiếm bom hydrogen khẩn cấp, và không có thời gian để thực hiện các thí nghiệm chính xác, xây dựng một lý thuyết hoàn toàn đáng tin cậy, cách của Craven là một cách khả thi.

Craven đã thu thập được kết quả của các cuộc gọi điện từ các chuyên gia, tổng hợp lại và vẽ ra một bản đồ xác suất vị trí của quả bom: chia toàn bộ khu vực có thể thành nhiều ô vuông nhỏ, mỗi ô vuông có giá trị xác suất khác nhau, có cao và thấp, giống như các đường cao tương đương cho thấy đỉnh núi và thung lũng trên bản đồ. Giống như những người lý trí xác định xem cô gái có độc thân hay không, Craven đã hoàn thành bước đầu tiên của phương pháp Bayesian.

Sau đó, Craven cùng với các chỉ huy của các đơn vị tìm kiếm bắt đầu tìm kiếm đạn thạch, đồng thời cập nhật xác suất cho mỗi lưới trong quá trình tìm kiếm, tuy nhiên, vị trí của các hình vuông có xác suất lớn nhất thường là các hẻm núi và vùng biển sâu trên đất liền, và thậm chí nếu đạn thạch thực sự ở đó, nó cũng không thể tìm thấy, vì vậy cần phải vẽ một bản đồ xác suất khác, cho thấy đạn thạch đã ở đó, có thể tìm thấy xác suất thạch thay vì xác suất vị trí của đạn thạch.

Chỉ hai năm sau, vào năm 1968, Craven đã có cơ hội để chơi một lần nữa, và lần nữa mất một quả bom hạch kim nhỏ, lần này Hải quân Hoa Kỳ mất một quả bom hạch kim lớn.

Vào tháng 6 năm 1968, tàu ngầm hạt nhân Swan của Hải quân Anh bị mất tích đột ngột ở vùng biển Azov ở Đại Tây Dương, và 99 sĩ quan hải quân trên tàu ngầm và tàu đều không có tin tức. Theo báo cáo điều tra sau sự việc, thủ phạm là một quả hoả hoạn kỳ lạ trên tàu ngầm, sau khi phóng ra, nó đã gây hấn cho tôi, quay đầu bắn vào chính mình, khiến đạn pháo nổ trong tàu ngầm.

Để tìm vị trí của Swan, Hải quân Hoa Kỳ đã tiến hành một cuộc tìm kiếm quy mô lớn, và Craven cũng tham gia. Do tốc độ du hành của tàu ngầm khi tai nạn nhanh, hướng đi, chiều hướng của tác động của vụ nổ, hướng của buồng lái tàu ngầm khi nổ là không rõ, ngay cả khi biết nơi tàu ngầm nổ, rất khó để xác định nơi mà mảnh vỡ tàu ngầm cuối cùng bị ngập nước biển.

Không có chuyên gia nào có thể ước tính chính xác những gì đã xảy ra với tàu ngầm trước và sau khi sự việc xảy ra, và cũng như trong việc tìm kiếm đạn thạch, Craven đã tham khảo ý kiến các nhà toán học, chuyên gia tàu ngầm và chuyên gia trong các lĩnh vực tìm kiếm hàng hải, viết ra các kịch bản giả mạo có thể, để họ đoán theo kiến thức và kinh nghiệm của họ về tình huống sẽ diễn ra theo hướng nào.

Cuối cùng, Craven đã có được một bản đồ xác suất của vùng biển 20 dặm. Toàn bộ vùng biển được chia thành nhiều lưới nhỏ, mỗi lưới nhỏ có hai giá trị xác suất p và q, p là xác suất tàu ngầm nằm trong lưới này, q là xác suất tìm kiếm nếu tàu ngầm nằm trong lưới. Theo kinh nghiệm, giá trị xác suất thứ hai chủ yếu liên quan đến độ sâu của vùng biển, và khả năng tàu ngầm thất bại tháo lưới trong vùng biển sâu sẽ cao hơn.

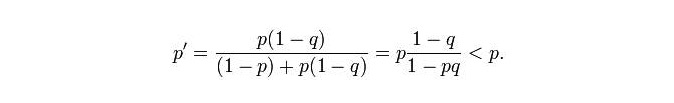
Trong khi đó, các tàu ngầm khác trong các mạng lưới khác sẽ có giá trị xác suất tăng lên:

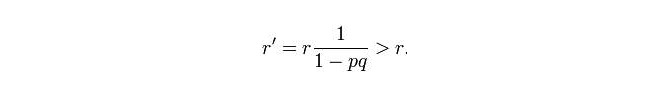
Mỗi lần tìm kiếm sẽ chọn một lưới có giá trị xác suất cao nhất của tàu ngầm trong toàn khu vực để tìm kiếm, nếu không được tìm thấy, bản phân bố xác suất sẽ được xoay một lần, và tàu tìm kiếm sẽ đi đến một lưới mới có giá trị đáng ngờ nhất để tìm kiếm, và tiếp tục như vậy cho đến khi tìm thấy thiên nga.

Ban đầu, các nhân viên hải quân dựa trên kinh nghiệm ước tính rằng tàu ngầm nằm ở phía đông của điểm nổ, thay vì lời khuyên của Craven và các nhà toán học khác, nhưng sau vài tháng tìm kiếm không có kết quả. Sau đó, Hải quân phải nghe theo lời khuyên của Craven, theo biểu đồ xác suất, tàu ngầm bị tai nạn nên ở phía tây của điểm nổ. Sau một vài lần tìm kiếm, tàu ngầm đã được tìm thấy ở đáy biển phía tây nam của điểm nổ.

Sau hai lần biểu diễn mạnh mẽ, phương pháp Bayes được Craven sử dụng trong tìm kiếm hàng hải dần dần được chấp nhận rộng rãi, từ đó, phương pháp Bayes bất ngờ thường xuyên xuất hiện cùng với bom hydrogen, tàu ngầm hạt nhân là từ khóa ở khắp mọi nơi. Trong nhiều thập kỷ, phương pháp Bayes đã được ứng dụng rộng rãi hơn, từ các từ khóa lọc tìm kiếm của google đến tổng hợp xe không người lái để xác định vị trí của mình, đi sâu vào mọi góc.

Tóm tắt từ Mô hình Toán học Đại học An Giang