Bảy kỹ thuật hồi quy bạn nên nắm vững

发明者量化-小小梦

tập trung vào tin nhắn riêng tư

tập trung vào

1271

Người theo dõi

Bảy kỹ thuật hồi quy bạn nên nắm vững

Được tạo ra trong: 2016-12-18 10:22:43, cập nhật trên: 2016-12-18 11:08:56

3121

Bảy kỹ thuật hồi quy bạn nên nắm vững

**Bài viết này giải thích về phân tích hồi quy và những ưu điểm của nó, tập trung tổng kết bảy kỹ thuật hồi quy phổ biến nhất và các yếu tố quan trọng của nó, bao gồm hồi quy tuyến tính, hồi quy logic, hồi quy đa phương thức, hồi quy từng bước, hồi quy cuộn, hồi quy xoắn, hồi quy ElasticNet, và cuối cùng giới thiệu các yếu tố quan trọng để chọn mô hình hồi quy đúng. ** ** Phân tích hồi quy bằng nút đệm là một công cụ quan trọng để mô hình hóa và phân tích dữ liệu. Bài viết này giải thích ý nghĩa của phân tích hồi quy và những ưu điểm của nó, tập trung vào tổng kết bảy kỹ thuật hồi quy phổ biến nhất và các yếu tố quan trọng của nó, bao gồm hồi quy tuyến tính, hồi quy logic, hồi quy đa phương thức, hồi quy từng bước, hồi quy cuộn, hồi quy xoắn, hồi quy ElasticNet, và cuối cùng giới thiệu các yếu tố quan trọng để chọn mô hình hồi quy đúng.**

### Phân tích hồi quy là gì?

Phân tích hồi quy là một kỹ thuật mô hình dự đoán, nghiên cứu mối quan hệ giữa các biến nhân (( mục tiêu) và các biến tự (( dự báo). Các kỹ thuật này thường được sử dụng trong phân tích dự đoán, mô hình chuỗi thời gian và mối quan hệ nhân quả giữa các biến phát hiện. Ví dụ, mối quan hệ giữa lái xe liều lĩnh của người lái xe và số lượng tai nạn giao thông đường bộ, phương pháp nghiên cứu tốt nhất là quay trở.

Phân tích hồi quy là một công cụ quan trọng để mô hình hóa và phân tích dữ liệu. Ở đây, chúng tôi sử dụng đường cong / đường để phù hợp với các điểm dữ liệu, theo cách này, khoảng cách từ đường cong hoặc đường đến điểm dữ liệu là tối thiểu. Tôi sẽ giải thích chi tiết điều này trong phần tiếp theo.

Bảy kỹ thuật hồi quy bạn nên nắm vững

### Tại sao chúng ta lại sử dụng phân tích hồi quy?

Như đã đề cập ở trên, Phân tích hồi quy ước tính mối quan hệ giữa hai hoặc nhiều biến. Dưới đây, chúng ta hãy đưa ra một ví dụ đơn giản để hiểu nó:

Ví dụ, trong điều kiện kinh tế hiện tại, bạn muốn ước tính doanh số bán hàng của một công ty. Bây giờ, bạn có dữ liệu mới nhất của công ty cho thấy doanh số bán hàng tăng khoảng 2,5 lần so với tăng trưởng kinh tế.

Sử dụng phân tích hồi quy có rất nhiều lợi ích:

Nó cho thấy mối quan hệ rõ rệt giữa biến tự và biến nhân.

Nó cho thấy cường độ ảnh hưởng của nhiều biến tự đối với một biến gây.

Phân tích hồi quy cũng cho phép chúng ta so sánh tác động của các biến đo lường các quy mô khác nhau, chẳng hạn như sự liên quan giữa biến đổi giá và số lượng hoạt động quảng cáo. Điều này có lợi cho các nhà nghiên cứu thị trường, nhà phân tích dữ liệu và nhà khoa học dữ liệu để loại trừ và ước tính một nhóm biến tốt nhất để xây dựng mô hình dự đoán.

### Chúng ta có bao nhiêu loại công nghệ quay trở lại?

Có rất nhiều kỹ thuật thu hồi khác nhau được sử dụng để dự đoán. Các kỹ thuật này chủ yếu có ba thước đo: số lượng biến tự, loại biến tự và hình dạng của đường thu hồi. Chúng tôi sẽ thảo luận chi tiết về chúng trong phần tiếp theo.

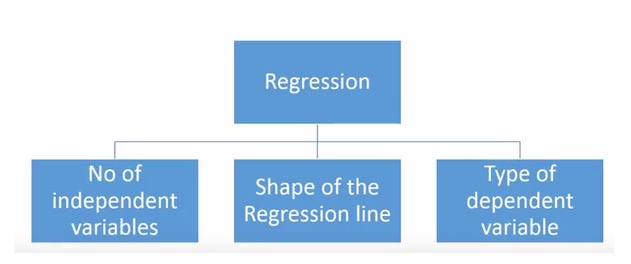
Bảy kỹ thuật hồi quy bạn nên nắm vững

Đối với những người sáng tạo, bạn thậm chí có thể tạo ra một mô hình hồi quy chưa được sử dụng nếu bạn cảm thấy cần thiết sử dụng một trong những tổ hợp các tham số trên. Nhưng trước khi bạn bắt đầu, hãy tìm hiểu về các phương pháp hồi quy thường được sử dụng như sau:

1. Linear Regression

Nó là một trong những kỹ thuật mô hình hóa nổi tiếng nhất. Phản hồi tuyến tính thường là một trong những kỹ thuật được lựa chọn khi người ta học mô hình dự đoán. Trong kỹ thuật này, vì biến là liên tục, biến tự có thể liên tục hoặc rời rạc, tính chất của đường thu hồi là tuyến tính.

Phản hồi tuyến tính sử dụng đường thẳng phù hợp nhất (đó là đường hồi) để thiết lập một mối quan hệ giữa biến nhân (y) và một hoặc nhiều biến tự (x).

Bạn có thể dùng một phương trình để biểu thị điều đó, Y=a+b.*X + e, trong đó a là độ cắt, b là độ lệch của đường thẳng, và e là số sai.

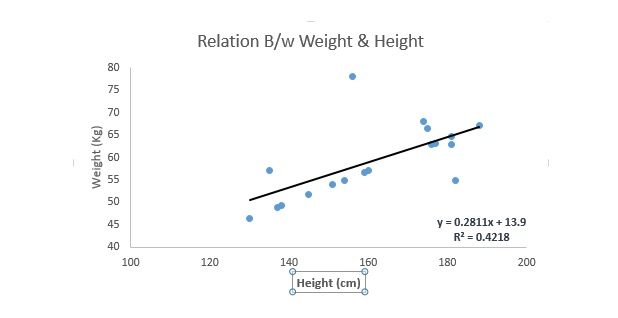
Sự khác biệt giữa hồi quy đơn tuyến và hồi quy đa tuyến là hồi quy đa tuyến có ((>1) biến tự, trong khi hồi quy đơn tuyến thường chỉ có một biến tự. Vấn đề bây giờ là làm thế nào để chúng ta có được một đường phù hợp tốt nhất?

Làm thế nào để có được giá trị của a và b?

Vấn đề này có thể được thực hiện dễ dàng bằng cách sử dụng phép nhân đôi tối thiểu. phép nhân đôi tối thiểu cũng là phương pháp được sử dụng nhiều nhất để tính toán đường hồi quy. Đối với dữ liệu quan sát, nó tính toán đường phù hợp tối ưu bằng cách giảm thiểu số lượng phương lệch vuông của mỗi điểm dữ liệu theo chiều dọc.

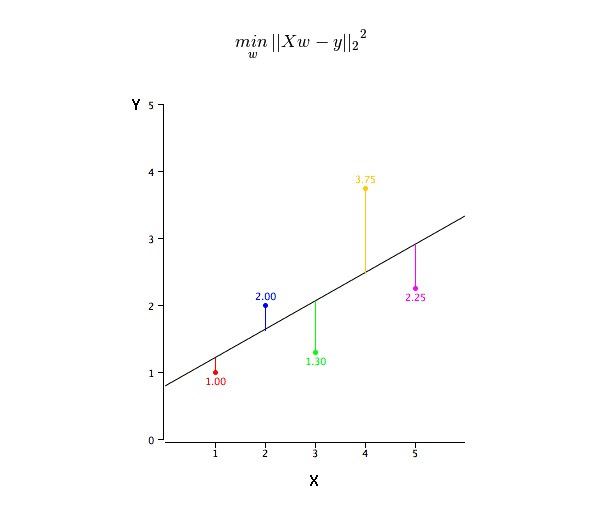
Chúng ta có thể sử dụng chỉ số R-square để đánh giá hiệu suất mô hình. Để biết chi tiết về các chỉ số này, bạn có thể đọc: Chỉ số hiệu suất mô hình Part 1, Part 2 .

Điểm mấu chốt:
- Sự liên hệ giữa biến tự và biến nhân phải là tuyến tính
- Thu hồi đa dạng có nhiều đồng tuyến tính, tự liên quan và khác biệt.
- Phản hồi tuyến tính rất nhạy cảm với các giá trị ngoại lệ. Nó sẽ ảnh hưởng nghiêm trọng đến đường thu hồi và cuối cùng ảnh hưởng đến giá trị dự đoán.
- Tính cộng tuyến tính đa sẽ làm tăng chênh lệch trong giá trị ước tính hệ số, làm cho ước tính rất nhạy cảm với những thay đổi nhỏ trong mô hình. Kết quả là ước tính hệ số không ổn định
- Trong trường hợp có nhiều biến tự, chúng ta có thể sử dụng phương pháp chọn trước, loại bỏ sau và lọc dần để chọn biến tự quan trọng nhất.
2. Logistic Regression

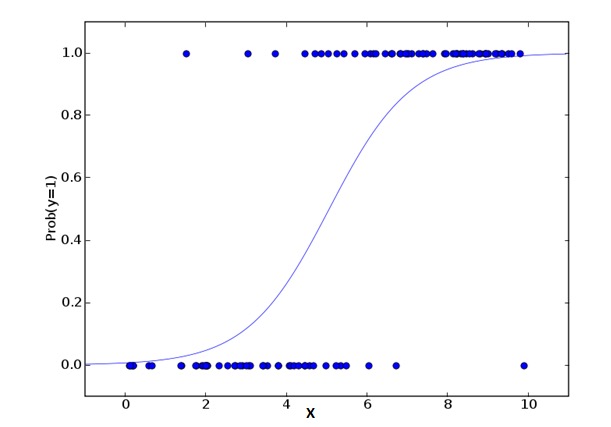
Logical regression được sử dụng để tính xác suất của sự kiện x = Success và sự kiện x = Failure. Chúng ta nên sử dụng logical regression khi các loại biến thuộc loại biến nhị phân ((¹⁄₀, true/false, yes/no). Ở đây, giá trị của Y là từ 0 đến 1, nó có thể được thể hiện bằng phương trình sau:
```
odds= p/ (1-p) = probability of event occurrence / probability of not event occurrence
ln(odds) = ln(p/(1-p))
logit(p) = ln(p/(1-p)) = b0+b1X1+b2X2+b3X3....+bkXk
```
Trong công thức trên, p thể hiện xác suất có một đặc điểm nào đó. Bạn nên hỏi một câu hỏi như: Tại sao chúng ta sử dụng logaritm trong công thức?

Vì ở đây chúng ta đang sử dụng phân phối nhị phân ((vì biến), chúng ta cần chọn một hàm kết nối tốt nhất cho phân phối này. Đó là hàm Logit. Trong phương trình trên, tham số được chọn bằng cách quan sát các giá trị ước tính rất giống của mẫu, thay vì tối thiểu hóa vuông và sai sót (như được sử dụng trong hồi quy thông thường).

Điểm mấu chốt:
- Nó được sử dụng rộng rãi trong các vấn đề phân loại.
- Logical regression không yêu cầu biến tự và biến nhân là mối quan hệ tuyến tính. Nó có thể xử lý các loại mối quan hệ khác nhau vì nó sử dụng một log chuyển đổi phi tuyến tính đối với chỉ số rủi ro tương đối OR dự đoán.
- Để tránh quá phù hợp và không phù hợp, chúng ta nên bao gồm tất cả các biến quan trọng. Một cách tốt để đảm bảo điều này là sử dụng phương pháp lọc từng bước để ước tính logical regression.
- Nó đòi hỏi một lượng mẫu lớn, bởi vì với số lượng mẫu nhỏ, hiệu quả ước tính rất có thể sẽ kém hơn so với số lượng mẫu nhỏ nhất thông thường.
- Các biến tự không nên liên quan đến nhau, tức là không có nhiều đồng tuyến tính. Tuy nhiên, trong phân tích và mô hình hóa, chúng ta có thể chọn bao gồm tác động của sự tương tác của các biến phân loại.
- Nếu giá trị của biến số là biến số theo thứ tự, nó được gọi là hồi quy logic theo thứ tự.
- Nếu biến số là đa dạng, nó được gọi là hồi quy logic đa dạng.
3. Polynomial Regression

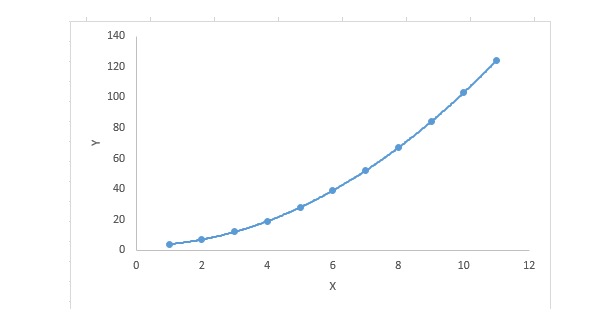
Đối với một phương trình hồi quy, nếu chỉ số của biến tự lớn hơn 1, thì nó là phương trình hồi quy đa thức. Như phương trình sau đây:
```
y=a+b*x^2
```
Trong kỹ thuật hồi quy này, đường phù hợp tốt nhất không phải là đường thẳng. Mà là một đường cong để phù hợp với điểm dữ liệu.

Ghi chú:
- Mặc dù sẽ có một sự dẫn dắt có thể phù hợp với một hàm đa hàm cấp cao và nhận được lỗi thấp hơn, nhưng điều này có thể dẫn đến quá phù hợp. Bạn cần thường xuyên vẽ biểu đồ quan hệ để xem sự phù hợp, và tập trung vào việc đảm bảo phù hợp hợp, không quá phù hợp và không thiếu phù hợp. Dưới đây là một biểu đồ có thể giúp hiểu:
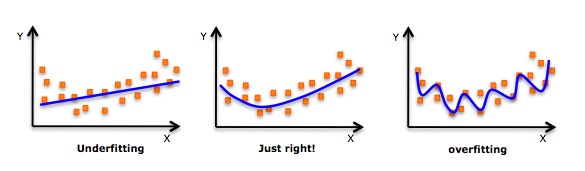
- Tìm các điểm đường cong rõ ràng ở hai đầu để xem các hình dạng và xu hướng này có ý nghĩa không. Các polynomial cấp cao hơn có thể cuối cùng sẽ tạo ra kết quả suy luận kỳ lạ.
4. Phục hồi từng bước

Chúng ta có thể sử dụng hình thức này khi xử lý nhiều biến tự. Trong kỹ thuật này, sự lựa chọn biến tự được thực hiện trong một quá trình tự động, bao gồm cả hoạt động không phải của con người.

Sự kiện này được thực hiện bằng cách quan sát các giá trị thống kê, như R-square, t-stats và chỉ số AIC, để xác định các biến quan trọng. Phục hồi từng bước phù hợp với mô hình bằng cách thêm / xóa đồng thời các biến tương ứng dựa trên tiêu chuẩn được chỉ định. Dưới đây là một số phương pháp thu hồi từng bước được sử dụng phổ biến nhất:
- Phương pháp suy thoái tiêu chuẩn làm hai việc: tăng và giảm dự đoán cần thiết cho mỗi bước.
- Phương pháp chọn tiếp theo bắt đầu với dự đoán nổi bật nhất trong mô hình và sau đó thêm các biến cho mỗi bước.
- Phương pháp loại bỏ backscatter bắt đầu cùng một lúc với tất cả các dự đoán của mô hình, sau đó loại bỏ các biến ít quan trọng nhất trong mỗi bước.
- Kỹ thuật mô hình hóa này nhằm mục đích sử dụng ít biến dự đoán nhất để tối đa hóa khả năng dự đoán. Đây cũng là một trong những cách xử lý các tập dữ liệu có chiều cao.
5. Phục hồi Ridge

Phân tích hồi quy là một kỹ thuật được sử dụng cho dữ liệu có nhiều đồng tuyến tính. Trong trường hợp đa đồng tuyến tính, mặc dù phép nhân đôi tối thiểu (OLS) là công bằng đối với mỗi biến, nhưng chúng có sự khác biệt lớn, khiến các giá trị quan sát bị lệch và xa giá trị thực. Phân hồi hồi quy làm giảm sai lệch tiêu chuẩn bằng cách tăng một độ lệch trên ước tính hồi quy.

Ở trên, chúng ta đã thấy phương trình hồi quy tuyến tính. Bạn có nhớ không? Nó có thể được thể hiện là:
```
y=a+ b*x
```
Phương trình này cũng có một phần sai. Phương trình hoàn chỉnh là:
```
y=a+b*x+e (error term),  [error term is the value needed to correct for a prediction error between the observed and predicted value]
=> y=a+y= a+ b1x1+ b2x2+....+e, for multiple independent variables.
```
Trong một phương trình tuyến tính, sai số dự đoán có thể được chia thành 2 phân số. Một là sai số và một là chênh lệch. Lỗi dự đoán có thể được gây ra bởi hai phân số này hoặc bất kỳ một trong hai.

Phục hồi nơ bằng cách rút gọn tham số λ ((lambda) để giải quyết vấn đề đồng tuyến tính đa. Xem công thức dưới đây

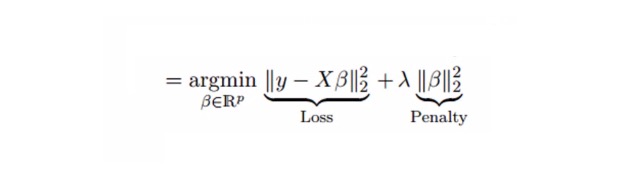
Trong công thức này, có hai thành phần. Đầu tiên là hàm số nhị phân nhỏ nhất, và thứ hai là λ của β2 ((β-squared), trong đó β là hệ số liên quan. Để thu hẹp tham số, hãy thêm nó vào hàm số nhị phân nhỏ nhất để có được một chênh lệch rất thấp.

Điểm mấu chốt:
- Giả định về sự hồi quy này tương tự như hồi quy nhỏ nhất của bội số trừ các số cố định.
- Nó thu hẹp giá trị của hệ số liên quan nhưng không đạt đến 0, cho thấy nó không có tính năng chọn đặc điểm
- Đây là một phương pháp chuẩn hóa, và nó sử dụng chuẩn hóa L2.
6. Lasso Regression

Nó tương tự như hồi quy nén, Lasso (Last Absolute Shrinkage and Selection Operator) cũng sẽ phạt kích thước tuyệt đối của hệ số hồi quy. Ngoài ra, nó có thể làm giảm mức độ thay đổi và tăng độ chính xác của mô hình hồi quy tuyến tính.

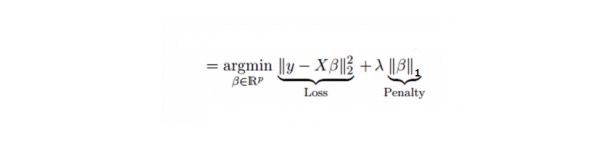
Phản hồi Lasso khác một chút so với Phản hồi Ridge, nó sử dụng hàm phạt là giá trị tuyệt đối, chứ không phải là bình phương. Điều này dẫn đến việc phạt ((hoặc bằng tổng giá trị tuyệt đối của ước tính ràng buộc) giá trị làm cho một số giá trị ước tính tham số bằng không. Sử dụng giá trị phạt càng lớn, ước tính thêm sẽ làm cho giá trị thu nhỏ gần bằng không. Điều này sẽ dẫn đến việc chúng ta phải chọn biến từ một số biến n được cung cấp.

Điểm mấu chốt:
- Giả định về sự hồi quy này tương tự như hồi quy nhỏ nhất của bội số trừ các số cố định.
- Nó có hệ số thu hẹp gần bằng 0 ([=0]) và điều này thực sự giúp chọn đặc điểm;
- Đây là một phương pháp chuẩn hóa, sử dụng chuẩn hóa L1;
- Nếu một nhóm biến dự đoán có liên quan cao, Lasso sẽ chọn một trong số các biến đó và thu hẹp các biến khác thành 0.
7. ElasticNet trở lại

ElasticNet là sự pha trộn giữa các kỹ thuật Lasso và Ridge regression. Nó sử dụng L1 để đào tạo và L2 được ưu tiên như một ma trận chính quy. ElasticNet rất hữu ích khi có nhiều đặc điểm liên quan.

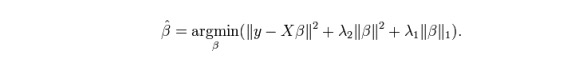
Lợi thế thực tế giữa Lasso và Ridge là nó cho phép ElasticNet kế thừa một số tính ổn định của Ridge trong trạng thái vòng lặp.

Điểm mấu chốt:
- Trong trường hợp các biến có liên quan cao, nó sẽ tạo ra hiệu ứng nhóm.
- Không có giới hạn về số lượng biến mà bạn có thể chọn.
- Nó có thể chịu được hai lần co lại.
- Ngoài 7 kỹ thuật quy tụ phổ biến nhất, bạn có thể xem các mô hình khác như Bayesian, Ecological và Robust regression.
Làm thế nào để chọn một mô hình regression đúng?

Cuộc sống thường rất đơn giản khi bạn chỉ biết một hoặc hai kỹ thuật. Một tổ chức đào tạo mà tôi biết đã nói với sinh viên của họ rằng nếu kết quả là liên tục, hãy sử dụng quy trình thu hồi tuyến tính. Nếu là nhị phân, hãy sử dụng quy trình thu hồi logic! Tuy nhiên, trong quá trình xử lý của chúng tôi, càng có nhiều lựa chọn, càng khó để chọn đúng.

Trong mô hình hồi quy đa dạng, việc lựa chọn kỹ thuật phù hợp nhất dựa trên loại biến tự và biến nhân, kích thước của dữ liệu và các đặc điểm cơ bản khác của dữ liệu là rất quan trọng. Dưới đây là các yếu tố quan trọng để bạn chọn mô hình hồi quy đúng:

Khám phá dữ liệu là một phần không thể thiếu trong việc xây dựng mô hình dự đoán. Nó nên là bước đầu tiên trong việc chọn mô hình phù hợp, chẳng hạn như xác định mối quan hệ và ảnh hưởng của các biến.

Để so sánh các ưu điểm của các mô hình khác nhau, chúng ta có thể phân tích các tham số chỉ số khác nhau, chẳng hạn như tham số có ý nghĩa thống kê, R-square, Adjusted R-square, AIC, BIC và các số sai sót, còn một là quy tắc Cp của Mallows. Điều này chủ yếu bằng cách so sánh mô hình với tất cả các mô hình con có thể (hoặc chọn chúng một cách cẩn thận), kiểm tra sự sai lệch có thể xuất hiện trong mô hình của bạn.

Xét nghiệm chéo là cách tốt nhất để đánh giá mô hình dự đoán. Ở đây, hãy chia bộ dữ liệu của bạn thành hai phần (một phần để đào tạo và một phần để xác minh). Sử dụng một chênh lệch đơn giản giữa giá trị quan sát và giá trị dự đoán để đo lường độ chính xác dự đoán của bạn.

Nếu bộ dữ liệu của bạn là nhiều biến hỗn hợp, thì bạn không nên chọn phương pháp chọn mô hình tự động vì bạn không muốn đặt tất cả các biến trong cùng một mô hình cùng một lúc.

Nó cũng sẽ phụ thuộc vào mục đích của bạn. Có thể có trường hợp một mô hình ít mạnh hơn sẽ dễ thực hiện hơn so với mô hình có ý nghĩa thống kê cao.

Phương pháp quy chuẩn hóa hồi quy ((Lasso, Ridge và ElasticNet) hoạt động tốt trong trường hợp có nhiều cộng tuyến giữa các biến dữ liệu có chiều cao và tập dữ liệu.