Hồi quy tuyến tính - phương pháp bình phương nhỏ nhất

• ### Lời khai

Trong thời gian này, việc học máy học , học Logistic regression của chương 5, cảm thấy khá khó khăn. Theo dõi nguồn gốc, từ Logistic regression đến linear regression , đến phép nhân đôi tối thiểu . Cuối cùng, định dạng đến toán học nâng cao (Sixth Edition; tập thứ hai) Chương chín, phần 10 phép nhân đôi tối thiểu , điều này hiểu được nguyên tắc toán học đằng sau phép nhân đôi tối thiểu xuất phát từ đâu. Hàm số nhỏ nhất của hàm số hai là một cách thực hiện để xây dựng công thức kinh nghiệm trong các vấn đề tối ưu hóa. Hiểu về nguyên tắc của nó sẽ rất hữu ích cho việc tìm hiểu về Hàm logistic regression và Hàm hỗ trợ máy vector học.

• ### B. Kiến thức cơ bản

Lịch sử của các phép toán số 2 nhỏ nhất rất thú vị.

Năm 1801, nhà thiên văn học người Ý Giuseppe Piazzi phát hiện ra tiểu hành tinh đầu tiên là Centauri. Sau 40 ngày theo dõi, Piazzi đã mất vị trí của Centauri vì Centauri đi phía sau Mặt trời. Các nhà khoa học trên toàn thế giới sau đó đã sử dụng dữ liệu quan sát của Piazzi để tìm kiếm Centauri, nhưng không có kết quả dựa trên kết quả mà hầu hết mọi người tính toán. Gauss, 24 tuổi, cũng đã tính toán quỹ đạo của Centauri.

Phương pháp của Gauss về phép nhân đôi nhỏ nhất được công bố vào năm 1809 trong cuốn sách Theory of the Movement of Celestial Bodies, và nhà khoa học người Pháp Le Gendre đã phát hiện ra phép nhân đôi nhỏ nhất một cách độc lập vào năm 1806, nhưng không được biết đến vì không được biết đến. Hai người đã tranh cãi về việc ai là người đầu tiên tạo ra nguyên tắc nhân đôi nhỏ nhất.

Năm 1829, Gauss cung cấp bằng chứng cho thấy hiệu quả tối ưu hóa của phép nhân đôi nhỏ nhất mạnh hơn các phương pháp khác, xem định lý Gauss-Markov.

• ### 3. Sử dụng kiến thức

Cốt lõi của phép tính nếp nhị phân nhỏ nhất của nếp nhị phân là đảm bảo tất cả các dữ liệu lệch phương và nhỏ nhất.

Giả sử chúng ta thu thập dữ liệu chiều dài và chiều rộng của một số tàu chiến.

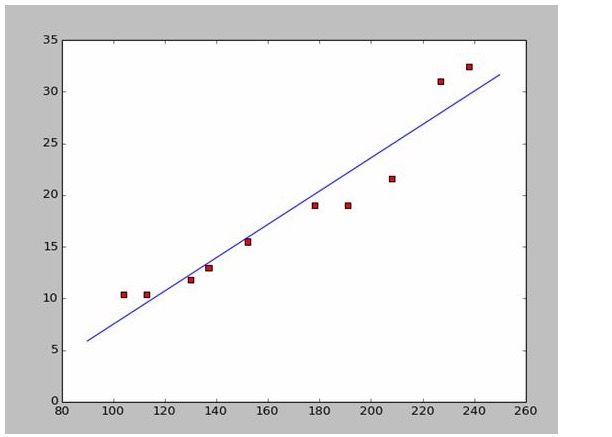
Dựa trên dữ liệu này, chúng tôi đã vẽ một bản đồ phân tán bằng Python:

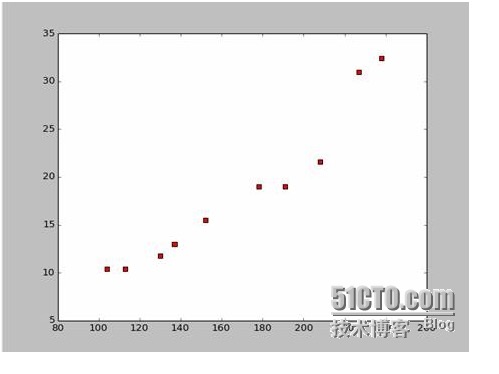
Có thể vẽ một bản đồ điểm phân tích như sau:

  import numpy as np                # -*- coding: utf-8 -*
  import os
  import matplotlib.pyplot as plt
  def drawScatterDiagram(fileName): # 改变工作路径到数据文件存放的地方
      os.chdir("d:/workspace_ml")
      xcord=[];ycord=[]
      fr=open(fileName)
      for line in fr.readlines():
          lineArr=line.strip().split()
          xcord.append(float(lineArr[1]));ycord.append(float(lineArr[2]))
      plt.scatter(xcord,ycord,s=30,c='red',marker='s')
      plt.show()

Nếu chúng ta lấy hai điểm trước là 238, 32, 4 và 152, 15, 5 chúng ta sẽ có hai phương trình. 152*a+b=15.5 328*a+b=32.4 Hãy giải cả hai phương trình này và chúng ta sẽ có a là 0,197 và b là -14,48. Trong trường hợp đó, chúng ta có thể có một biểu đồ tương ứng như thế này:

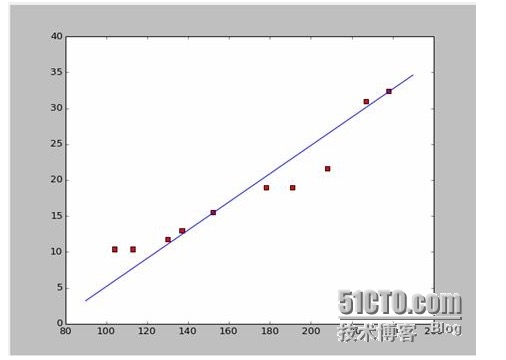
Vâng, câu hỏi mới là a, b có phải là giải pháp tối ưu hay không? Nói một cách chuyên nghiệp là: a, b có phải là tham số tối ưu của mô hình không? Trước khi trả lời câu hỏi này, chúng ta hãy giải quyết một câu hỏi khác:

Câu trả lời là: đảm bảo rằng tất cả các dữ liệu đều lệch bình phương và tối thiểu. Về nguyên tắc, chúng ta sẽ nói về sau, trước tiên hãy xem cách sử dụng công cụ này để tính toán a và b tốt nhất.

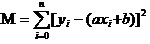
Bây giờ chúng ta sẽ tìm ra a và b nhỏ nhất của M.

Vậy thì phương trình này thực sự là một hàm số nhị phân với a, b là biến số tự và M là biến số nhân.

Hãy nhớ lại cách các hàm đơn vị đối với các hàm số cao có giá trị cực. Chúng ta sử dụng hàm hàm số. Trong hàm số nhị phân, chúng ta vẫn sử dụng hàm số. Chỉ có điều là hàm số ở đây có tên mới là hàm số định hướng. Chúng ta có một tập hợp các phương trình bằng cách tìm định hướng cho M.

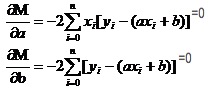
Trong cả hai phương trình này, cả hai phương trình x và y đều được biết.

Một cách dễ dàng để tìm a và b. Vì chúng tôi sử dụng dữ liệu từ Wikipedia, tôi sẽ vẽ một hình ảnh phù hợp với câu trả lời của bạn:

  # -*- coding: utf-8 -*importnumpy as npimportosimportmatplotlib.pyplot as pltdefdrawScatterDiagram(fileName):
  # 改变工作路径到数据文件存放的地方os.chdir("d:/workspace_ml")xcord=[];
  # ycord=[]fr=open(fileName)forline infr.readlines():lineArr=line.strip().split()xcord.append(float(lineArr[1]));
  # ycord.append(float(lineArr[2]))plt.scatter(xcord,ycord,s=30,c='red',marker='s')
  # a=0.1965;b=-14.486a=0.1612;b=-8.6394x=np.arange(90.0,250.0,0.1)y=a*x+bplt.plot(x,y)plt.show()
  # -*- coding: utf-8 -*
  import numpy as np
  import os
  import matplotlib.pyplot as plt
  def drawScatterDiagram(fileName):
      #改变工作路径到数据文件存放的地方
      os.chdir("d:/workspace_ml")
      xcord=[];ycord=[]
      fr=open(fileName)
      for line in fr.readlines():
          lineArr=line.strip().split()
          xcord.append(float(lineArr[1]));ycord.append(float(lineArr[2]))
      plt.scatter(xcord,ycord,s=30,c='red',marker='s')
      #a=0.1965;b=-14.486
      a=0.1612;b=-8.6394
      x=np.arange(90.0,250.0,0.1)
      y=a*x+b
      plt.plot(x,y)
      plt.show()

• ### Bốn nguyên tắc

Tại sao trong dữ liệu phù hợp, chúng ta nên cho phép các số liệu dự đoán của mô hình với sự khác biệt của các số liệu thực tế bằng bình phương thay vì các giá trị tuyệt đối và tối thiểu để tối ưu hóa các tham số mô hình?

Câu hỏi này đã được trả lời, xem liên kết (http://blog.sciencenet.cn/blog-430956-621997.html)

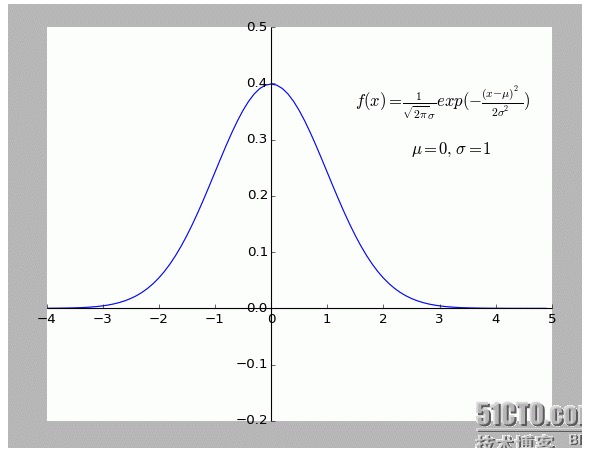
Cá nhân tôi cảm thấy giải thích này rất thú vị. Đặc biệt là giả định bên trong: tất cả các điểm lệch khỏi f (x) đều có tiếng ồn.

Một điểm lệch càng xa nghĩa là tiếng ồn càng lớn, thì xác suất xuất hiện của điểm này càng nhỏ. Vậy độ lệch x có liên quan gì đến xác suất xuất hiện f (x)?

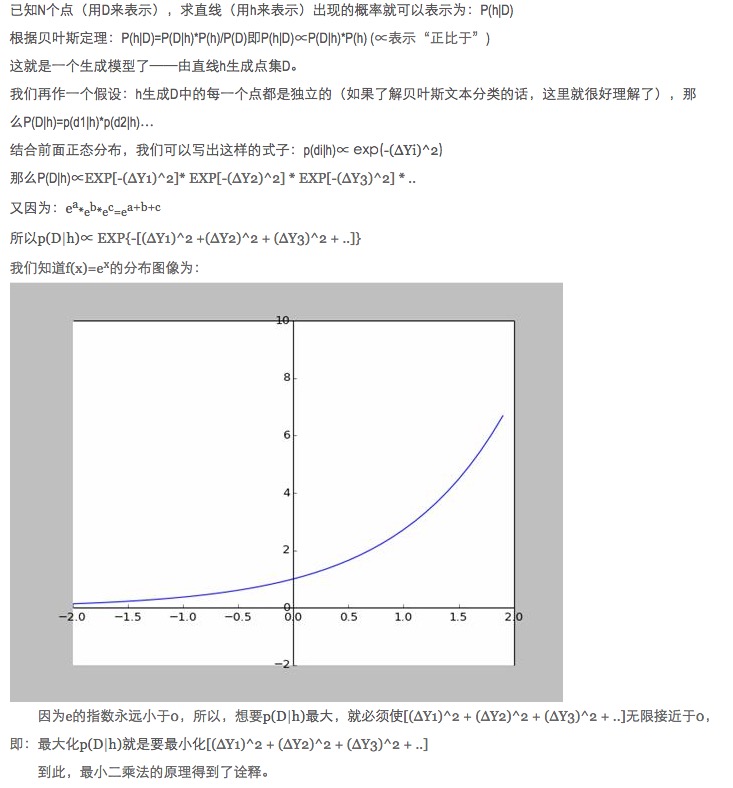
• ### V, mở rộng.

Tất cả những điều trên đều là hai chiều, nghĩa là chỉ có một biến tự. Nhưng trong thế giới thực, ảnh hưởng đến kết quả cuối cùng là sự chồng lên nhau của nhiều yếu tố, nghĩa là có nhiều biến tự.

Đối với các hàm siêu tuyến tính N chung, sử dụng ma trận ngược trong chuỗi đại số tuyến tính để tìm giải là OK; vì tạm thời không tìm thấy ví dụ phù hợp, hãy dùng nó như một hàm dẫn và ở đây.

Tất nhiên, thiên nhiên là một sự phù hợp đa dạng hơn là một sự phù hợp tuyến tính đơn giản, đó là một thứ cao cấp hơn.

• Tài liệu tham khảo

  • Phương pháp toán học cao cấp (Bản thứ sáu)
  • Phương pháp đại số tuyến tính (Beijing University Press)
  • Tác giả:Nhân số 2 nhỏ nhất
  • Wikipedia: phép nhân đôi nhỏ nhất
  • ScienceNet:Khoảng cách nhỏ nhất của số hai là bao nhiêu?

Tác phẩm gốc, cho phép chuyển tiếp, khi chuyển tiếp, hãy chắc chắn đánh dấu nguồn gốc của bài viết, thông tin về tác giả và tuyên bố này bằng cách sử dụng siêu liên kết. Nếu không, sẽ bị truy tố pháp lý.