Sự hiểu biết thú vị về Naive Bayes

NavieBayes

  Nhiều trường hợp trong cuộc sống cần phân loại, chẳng hạn như phân loại tin tức, phân loại bệnh nhân và các trường hợp sử dụng thực tế. Để giúp mọi người có thể hiểu được hình ảnh, bài viết này giới thiệu một thuật toán phân loại phổ biến đơn giản từ ứng dụng thực tế - Bayes đơn giản (Navie Bayes classifier).

• 01 Ví dụ về phân loại bệnh nhân

Hãy để tôi bắt đầu bằng một ví dụ, bạn sẽ thấy phân loại Bayes là rất dễ hiểu, không khó chút nào. Một bệnh viện đã nhận được sáu bệnh nhân nhập viện vào buổi sáng, như biểu đồ dưới đây.

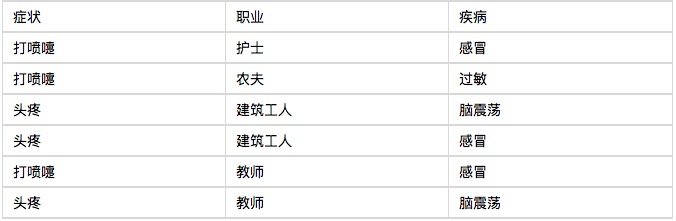
Bây giờ đến bệnh nhân thứ bảy, một công nhân xây dựng hắt hơi.

  P(A|B) = P(B|A) P(A) / P(B)

Có thể:

  P(感冒|打喷嚏x建筑工人) 
  　　　　= P(打喷嚏x建筑工人|感冒) x P(感冒) 
  　　　　/ P(打喷嚏x建筑工人)

Giả sử hai tính năng “thịt hắt” và “nhà công nhân xây dựng” là hai tính năng độc lập, thì phương trình trên sẽ trở thành

  P(感冒|打喷嚏x建筑工人) 
  　　　　= P(打喷嚏|感冒) x P(建筑工人|感冒) x P(感冒)
  　　　　/ P(打喷嚏) x P(建筑工人)

Nó có thể được tính toán.

  P(感冒|打喷嚏x建筑工人) 
  　　　　= 0.66 x 0.33 x 0.5 / 0.5 x 0.33 
  　　　　= 0.66

Vì vậy, người công nhân xây dựng hắt hơi này có 66% khả năng bị cảm lạnh. Đồng thời, có thể tính xác suất bệnh nhân bị dị ứng hoặc chấn thương não. So sánh các xác suất này để biết bệnh gì có thể xảy ra với anh ta.

Đây là phương pháp cơ bản của bộ phân loại Bayesian: dựa trên dữ liệu thống kê, tính toán xác suất của từng loại dựa trên một số đặc điểm, để thực hiện phân loại.

• 02 Công thức của bộ phân loại Bayes đơn giản

Giả sử một cá nhân có n đặc điểm, F1, F2, … , Fn. Có m loại cá nhân, C1, C2, … , Cm. Phân loại Bayes là phân loại có xác suất lớn nhất, đó là giá trị tối đa của thuật toán sau:

  P(C|F1F2...Fn) 
  　　   = P(F1F2...Fn|C)P(C) / P(F1F2...Fn)

Vì P ((F1F2…Fn) là giống nhau cho tất cả các loại, có thể bỏ qua, vấn đề trở thành

  P(F1F2...Fn|C)P(C)

Giá trị tối đa

Các phân loại Bayesian đơn giản đi xa hơn, giả định rằng tất cả các đặc điểm đều độc lập với nhau, do đó

  P(F1F2...Fn|C)P(C) 
  　　   = P(F1|C)P(F2|C) ... P(Fn|C)P(C)

Mỗi phần tử bên phải của phương trình trên có thể được lấy từ dữ liệu thống kê, từ đó có thể tính xác suất của mỗi loại tương ứng, để tìm ra loại có xác suất lớn nhất.

Mặc dù giả định “tất cả các đặc điểm độc lập với nhau” không có khả năng thực hiện trong thực tế, nhưng nó có thể đơn giản hóa tính toán rất nhiều và nghiên cứu cho thấy nó không ảnh hưởng nhiều đến độ chính xác của kết quả phân loại.

Dưới đây là hai ví dụ khác về cách sử dụng phân loại Bayes đơn giản.

• 03 Xác định tài khoản

Theo thống kê của một trang web cộng đồng, trong số 10.000 tài khoản, có 89% là tài khoản thực (đặt C0) và 11% là tài khoản giả (đặt C1). Tiếp theo, bạn cần sử dụng số liệu thống kê để đánh giá tính xác thực của một tài khoản.

  C0 = 0.89 C1 = 0.11

Giả sử một tài khoản có ba đặc điểm sau: F1: Số ngày đăng ký / số ngày đăng ký F2: Số lượng bạn bè/số ngày đăng ký F3: Có sử dụng TrueHeadImage (trueHeadImage là 1, không phải TrueHeadImage là 0) F1 = 0.1  F2 = 0.2  F3 = 0

Hãy hỏi xem tài khoản đó là tài khoản thật hay giả. Cách tính là sử dụng bộ phân loại Bayes đơn giản để tính giá trị của phương thức tính toán dưới đây.

P(F1|C)P(F2|C)P(F3|C)P©

Mặc dù các giá trị trên có thể được lấy từ số liệu thống kê, nhưng có một vấn đề ở đây: F1 và F2 là các biến liên tục, không phù hợp để tính xác suất theo một giá trị cụ thể. Một thủ thuật là chuyển giá trị liên tục thành giá trị rời rạc, tính xác suất của khoảng cách.[0, 0.05]、(0.05, 0.2)、[0.2, +∞] ba khoảng, sau đó tính xác suất của mỗi khoảng. Trong ví dụ của chúng tôi, F1 bằng 0.1, rơi vào khoảng thứ hai, vì vậy khi tính toán, sử dụng xác suất của khoảng thứ hai.

Theo thống kê, có:

P(F1|C0) = 0.5, P(F1|C1) = 0.1  P(F2|C0) = 0.7, P(F2|C1) = 0.2  P(F3|C0) = 0.2, P(F3|C1) = 0.9

Vì vậy,

P(F1|C0) P(F2|C0) P(F3|C0) P(C0)  = 0.5 x 0.7 x 0.2 x 0.89  = 0.0623 P(F1|C1) P(F2|C1) P(F3|C1) P(C1)  = 0.1 x 0.2 x 0.9 x 0.11  = 0.00198 Bạn có thể thấy rằng mặc dù người dùng này không sử dụng hình ảnh thực tế, nhưng khả năng tài khoản này là tài khoản thực tế cao hơn 30 lần so với tài khoản giả mạo, do đó nó được đánh giá là có thật.

• 04 Phân loại giới tính

Dưới đây là một số liệu thống kê về các đặc điểm của cơ thể con người.

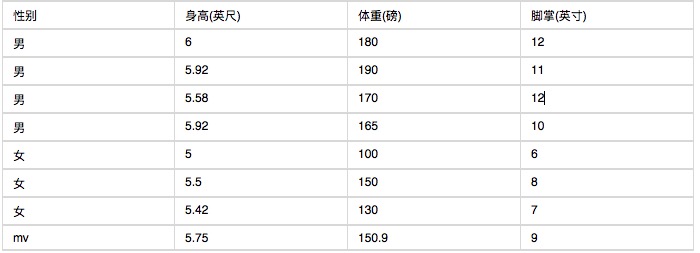
Nếu bạn biết một người có chiều cao 6 feet, nặng 130 pounds, bàn chân 8 inch, bạn có thể hỏi người đó là nam hay nữ không?

P (trị cao và giới tính) x P (trọng lượng và giới tính) x P (chân và bàn tay và giới tính) x P (giới tính)

Khó khăn ở đây là vì chiều cao, trọng lượng, bàn chân là các biến liên tục, không thể tính xác suất bằng phương pháp biến rời rạc. Và vì mẫu quá nhỏ, không thể tính theo khoảng. Làm thế nào?

Với dữ liệu này, chúng ta có thể tính toán phân loại giới tính.

P (tăng = 6 tuổi) x P (trọng lượng = 130 tuổi) x P (bàn chân = 8 tuổi) x P (người đàn ông)

= 6.1984 x e-9

P (tăng = 6 tuổi) x P (trọng lượng = 130 tuổi) x P (bàn chân = 8 tuổi) x P (nữ)

= 5.3778 x e-4

Có thể thấy rằng phụ nữ có khả năng mắc bệnh cao gấp gần 10.000 lần so với nam giới, vì vậy người đó là phụ nữ.

Bài đăng này được đăng tải trên trang WeChat của Weibo.