Hiểu biết trực quan về sự đồng tích hợp

Hướng dẫn: Bài viết này nhằm giới thiệu khái niệm tổng hợp một cách trực quan, giúp mọi người hiểu được ý nghĩa cơ bản của nó, động cơ của khái niệm này và các trường hợp ứng dụng đơn giản.

• Thông tin tổng hợp

Ở đây tôi chỉ muốn chỉ ra một định nghĩa trực quan về tính tổng hợp, không liên quan đến định nghĩa của các ký hiệu toán học nghiêm ngặt và suy ra các công thức nghiêm ngặt.

Nếu bạn quan tâm, bạn có thể tham khảo: Wikipedia Cointegration.

Tại sao phải đồng nhất?

Trong khi đó, những người dân Việt Nam vẫn còn sống trong tình trạng bất ổn.

Nói một cách đơn giản, ổn định là một tính chất của một dãy không thay đổi trong thời gian, và nó là một tính chất mà chúng ta rất thích khi thực hiện các dự đoán phân tích của dữ liệu. Nếu một bộ dữ liệu dãy thời gian là ổn định, điều đó có nghĩa là các giá trị trung bình và chênh lệch của nó không thay đổi, vì vậy chúng ta có thể dễ dàng sử dụng một số kỹ thuật thống kê trên dãy. Chúng ta hãy xem một ví dụ để hiểu xem dãy ổn định và không ổn định trông như thế nào.

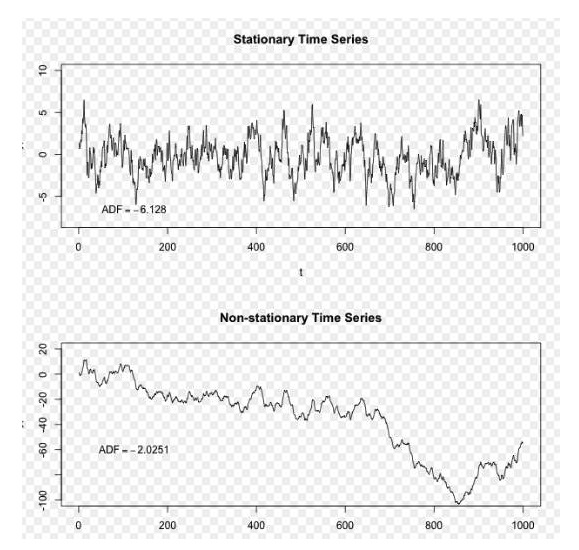
Hình ảnh: Wikipedia

Trong biểu đồ trên, chuỗi phía trên là một chuỗi ổn định, và chúng ta có thể thấy rằng nó luôn luôn dao động xung quanh một trung bình dài hạn, chuỗi phía dưới là một chuỗi không ổn định, và chúng ta có thể thấy rằng trung bình dài hạn của nó thay đổi.

Ví dụ về ứng dụng, nếu một chuỗi giá của một tài sản (hoặc giá của hai chuỗi) là ổn định, thì khi nó lệch khỏi giá trung bình của nó, người ta có thể mong đợi giá sẽ quay trở lại mức trung bình này vào một thời điểm trong tương lai. Chúng ta có thể sử dụng tính chất này để đầu tư và thu lợi nhuận. Giả sử một cổ phiếu có giá trung bình dài hạn là 9 đô la và giá trị hiện tại là 8 đô la. Nếu sau khi kiểm tra, chúng tôi cho rằng chuỗi lịch sử của cổ phiếu này có tính chất ổn định, và giả định rằng sự ổn định này có thể được duy trì, bạn có thể mua cổ phiếu này và chờ đợi giá của nó quay trở lại 9 đô la trong tương lai, thu được 1 đô la lợi nhuận.

Đây là một chuỗi giá cổ phiếu có tính ổn định:

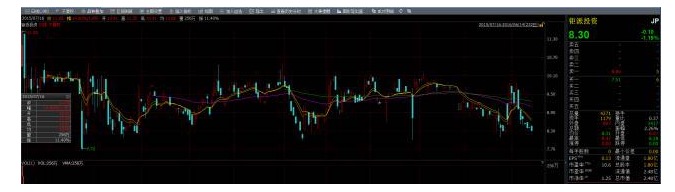
Sự ổn định là rất hữu ích, nhưng trong thực tế, phần lớn các cổ phiếu đều không ổn định, vậy liệu chúng ta có thể tận dụng tính chất ổn định để kiếm lợi nhuận không? Câu trả lời là có, khi đó cointegration xuất hiện! Nếu hai nhóm chuỗi không ổn định, nhưng kết hợp tuyến tính của chúng có thể có được một chuỗi ổn định, thì chúng ta nói rằng hai nhóm dữ liệu chuỗi thời gian này có tính chất hợp nhất, chúng ta cũng có thể sử dụng tính chất thống kê cho chuỗi của nhóm này.

Ví dụ, khi hai nhóm dữ liệu chuỗi thời gian khác nhau đều đặn, chúng ta có thể đầu tư lợi nhuận dựa trên sự ổn định của sự khác biệt này: khi giá cả của hai cổ phiếu khác nhau quá lớn, theo sự ổn định chúng ta dự đoán rằng chênh lệch giá sẽ thu hẹp, do đó mua cổ phiếu giá thấp, bán cổ phiếu giá cao và chờ đợi giá quay trở lại để kiếm lợi nhuận.

Đây là nguồn gốc của giao dịch cặp.

• Sự ổn định và phương pháp kiểm tra

Nói một cách nghiêm ngặt, tính ổn định có thể được chia thành hai loại: ổn định chặt chẽ (strictly stationary) và ổn định yếu (weak stationary). Cần ổn định chặt chẽ là một chuỗi luôn có hàm phân phối không thay đổi, trong khi ổn định yếu là một chuỗi có số liệu thống kê mô tả của các hằng số không thay đổi. Tất cả các chuỗi ổn định mạnh đều đáp ứng tính ổn định yếu, nhưng ngược lại không đúng.

Một ví dụ về ứng dụng

Đầu tiên, cần lưu ý rằng mối quan hệ thống nhất không phải là mối quan hệ liên quan. Chúng ta đã tạo ra hai nhóm dữ liệu nhân tạo, từ đó nhìn trực quan hơn vào mối quan hệ thống nhất. import numpy as np import pandas as pd import seaborn import statsmodels import matplotlib.pyplot as plt from statsmodels.tsa.stattools import coint

Dữ liệu cấu trúc

Đầu tiên, chúng ta xây dựng hai nhóm dữ liệu, mỗi nhóm có chiều dài 100 ⋅ số liệu nhóm đầu tiên là 100 cộng với một phần xu hướng xuống và một phân bố chính xác tiêu chuẩn ⋅ số liệu nhóm thứ hai dựa trên số liệu nhóm đầu tiên cộng 30, và thêm một phân bố chính xác tiêu chuẩn bổ sung ⋅ có

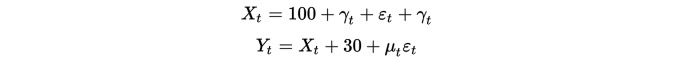
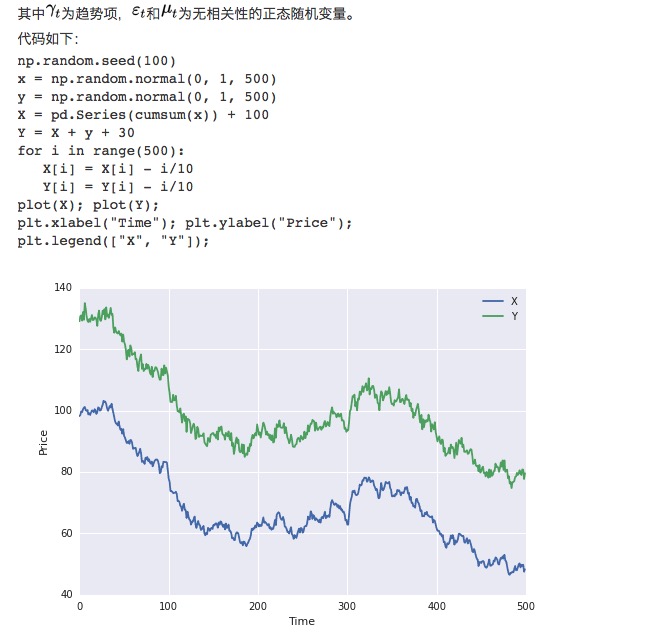
Rõ ràng, cả hai nhóm dữ liệu đều không ổn định, bởi vì các giá trị trung bình thay đổi theo thời gian. Nhưng cả hai nhóm dữ liệu có mối quan hệ đối xứng, bởi vì chuỗi phân số của chúng đều ổn định:

plot(Y-X); plt.axhline((Y-X).mean(),color=“red”, linestyle=“–”); plt.xlabel(“Time”); plt.ylabel(“Price”); plt.legend([“Y-X”, “Mean”]);

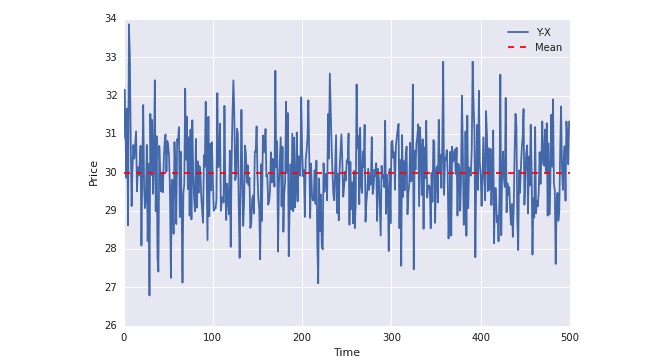
Trong biểu đồ trên, có thể thấy rằng đường xanh luôn dao động xung quanh giá trị trung bình.

• Kết luận

Nếu chúng ta nói về tổng hợp hoàn toàn từ góc độ toán học, nó sẽ phức tạp hơn, và các lớp học định lượng sau này sẽ có liên quan. Chúng tôi chỉ làm một giới thiệu đơn giản về mức độ hiểu của [level- 0], mục đích là để mọi người kết hợp tốt hơn tổng hợp với ứng dụng thực tế.

Hãy cùng chia sẻ, chuyển sang lớp học định lượng.