Ứng dụng Python Naive Bayes

Giả sử rằng các biến dự đoán là độc lập với nhau, theo định lý Bayes, bạn có thể có được phương pháp phân loại Bayes đơn giản. Nói một cách đơn giản hơn, một bộ phân loại Bayes đơn giản giả định một tính năng của phân loại không liên quan đến các tính năng khác trong phân loại đó. Ví dụ, nếu một trái cây là tròn và đỏ, và có đường kính khoảng 3 inch, thì trái cây có thể là quả táo.

• #### Mô hình Bayes đơn giản rất dễ xây dựng và rất hữu ích đối với các tập dữ liệu lớn. Mặc dù đơn giản, nhưng hiệu suất của Bayes đơn giản vượt quá các phương pháp phân loại rất phức tạp.

Định lý của Bayes cung cấp một phương pháp để tính xác suất hậu nghiệm P (c/x) từ P ©, P (x) và P (x). Xem phương trình sau:

Ở đây,

P ((c 11:3x) là xác suất hậu nghiệm của lớp (đối tượng) với giả định rằng biến dự đoán (đặc tính) đã được biết đến P © là xác suất tiên quyết của lớp P (x) là xác suất, tức là xác suất dự đoán của một biến giả định một loại đã biết. P (x) là xác suất tiên lượng của biến dự đoán Ví dụ: Hãy dùng một ví dụ để hiểu khái niệm này. Dưới đây, tôi có một tập huấn luyện về thời tiết và biến mục tiêu tương ứng là Play. Bây giờ, chúng ta cần phân loại những người tham gia sẽ chơi và không chơi theo thời tiết.

Bước 1: Chuyển tập dữ liệu thành bảng tần số

Bước 2: Tạo biểu đồ likelihood bằng cách sử dụng một con lắc tương tự với xác suất 0.64 con lắc khi Overcast là 0.29.

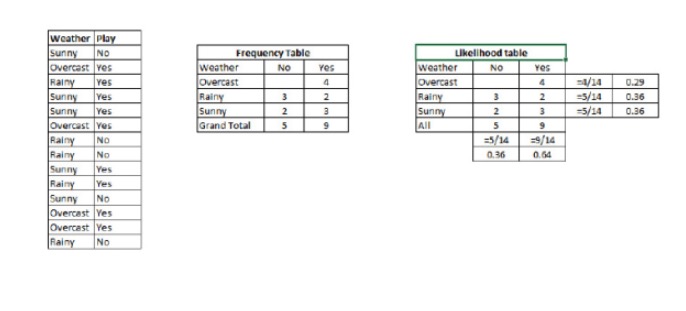
Bước 3: Bây giờ, sử dụng phương trình Bayes đơn giản để tính toán xác suất của mỗi loại.

Câu hỏi: Người chơi có thể chơi nếu thời tiết đẹp không?

Chúng ta có thể sử dụng phương pháp mà chúng ta đã thảo luận để giải quyết vấn đề này. Vì vậy P (Chơi) = P (Chơi) * P (Chơi) / P (Chơi)

Chúng ta có P là ³⁄₉ = 0.33, P là ⁵⁄₁₄ = 0.36, P là ⁹⁄₁₄ = 0.64.

Bây giờ, P (được chơi) = 0.33 * 0.64 / 0.36 = 0.60, có xác suất lớn hơn.

Bayes đơn giản sử dụng một phương pháp tương tự để dự đoán xác suất của các loại khác nhau thông qua các thuộc tính khác nhau. Thuật toán này thường được sử dụng để phân loại văn bản, cũng như các vấn đề liên quan đến nhiều loại.

• #### Mã Python:

  #Import Library
  from sklearn.naive_bayes import GaussianNB
  　　
  #Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset

Create SVM classification object model = GaussianNB()

there is other distribution for multinomial classes like Bernoulli Naive Bayes, Refer link

Train the model using the training sets and check score

model.fit(X, y) #Predict Output predicted= model.predict(x_test)