Suy nghĩ về các chiến lược giao dịch tần suất cao (1)
 3
3
 4856
4856

Bài viết thảo luận về các chiến lược giao dịch tần suất cao của tiền kỹ thuật số, bao gồm các nguồn lợi nhuận (chủ yếu từ biến động thị trường và hoàn phí giao dịch), các vấn đề về đặt lệnh và kiểm soát vị thế, cũng như phương pháp mô hình hóa khối lượng giao dịch bằng phân phối Pareto. Ngoài ra, dữ liệu giao dịch và lệnh tối ưu do Binance cung cấp đã được sử dụng để kiểm tra ngược và các vấn đề khác về chiến lược giao dịch tần suất cao dự kiến sẽ được thảo luận sâu hơn trong các bài viết tiếp theo.
Tôi đã viết hai bài viết về giao dịch tần suất cao của tiền kỹ thuật số trước đây. Giới thiệu chi tiết về các chiến lược tần suất cao dành cho tiền kỹ thuật số, Kiếm được 80 lần trong 5 ngày, sức mạnh của chiến lược tần suất cao. Nhưng nó chỉ có thể được coi là việc chia sẻ kinh nghiệm và nói chuyện chung. Lần này tôi dự định viết một loạt bài viết để giới thiệu những ý tưởng về giao dịch tần suất cao ngay từ đầu. Tôi hy vọng sẽ trình bày ngắn gọn và rõ ràng nhất có thể. Tuy nhiên, do trình độ hạn chế và hiểu biết sâu sắc của tôi về giao dịch tần suất cao giao dịch, bài viết này chỉ là điểm khởi đầu. Tôi hy vọng các chuyên gia có thể sửa lỗi cho tôi.
Nguồn lợi nhuận tần suất cao
Như đã đề cập trong các bài viết trước, các chiến lược tần suất cao đặc biệt phù hợp với các thị trường có biến động cực độ. Kiểm tra sự thay đổi giá của một sản phẩm giao dịch trong một thời gian ngắn, bao gồm xu hướng và biến động chung. Nếu chúng ta có thể dự đoán chính xác những thay đổi trong xu hướng, chúng ta chắc chắn có thể kiếm được tiền, nhưng đây cũng là điều khó khăn nhất. Bài viết này chủ yếu giới thiệu các chiến lược của nhà sản xuất tần suất cao và sẽ không đề cập đến vấn đề này. Trong một thị trường biến động, nếu chiến lược đặt lệnh tăng và giảm được thực hiện đủ thường xuyên và biên lợi nhuận đủ lớn thì có thể bù đắp được những khoản lỗ có thể xảy ra do xu hướng, do đó bạn có thể kiếm được lợi nhuận mà không cần dự đoán thị trường. Hiện tại, tất cả các giao dịch của nhà sản xuất trên sàn giao dịch đều được hoàn tiền phí giao dịch, đây cũng là một thành phần của lợi nhuận. Cạnh tranh càng gay gắt thì tỷ lệ hoàn tiền càng cao.
Vấn đề cần giải quyết
Chiến lược này đặt lệnh mua và lệnh bán cùng lúc. Câu hỏi đầu tiên là đặt lệnh ở đâu. Lệnh càng gần thị trường thì khả năng giao dịch càng cao. Tuy nhiên, trong một thị trường biến động, giá giao dịch tức thời có thể cách xa thị trường. Nếu lệnh được đặt quá gần, bạn sẽ không thể có đủ lợi nhuận. Xác suất thực hiện các lệnh đặt ở khoảng cách quá xa là thấp. Đây là vấn đề cần được tối ưu hóa.
Kiểm soát vị trí của bạn. Để kiểm soát rủi ro, chiến lược không thể tích lũy quá nhiều vị thế trong thời gian dài. Có thể giải quyết vấn đề này bằng cách kiểm soát khoảng cách đặt hàng, số lượng đặt hàng, tổng giới hạn vị thế, v.v.
Để đạt được các mục tiêu trên, cần phải mô hình hóa và ước tính xác suất giao dịch, lợi nhuận giao dịch, ước tính thị trường và các khía cạnh khác. Có nhiều bài viết và bài báo trong lĩnh vực này, có thể được tìm thấy với các từ khóa như Giao dịch tần suất cao , Sổ lệnh, v.v. Có nhiều lời khuyên trên mạng nhưng tôi sẽ không đề cập ở đây. Ngoài ra, tốt nhất là thiết lập một hệ thống kiểm tra ngược đáng tin cậy và nhanh chóng. Mặc dù các chiến lược tần suất cao có thể dễ dàng được xác minh thông qua giao dịch thực tế để xác minh hiệu quả của chúng, nhưng kiểm tra ngược vẫn có thể cung cấp nhiều ý tưởng hơn và giảm chi phí thử nghiệm và sai sót.
Dữ liệu bắt buộc
Binance cung cấp dữ liệu giao dịch theo từng giao dịch và thứ tự tốt nhấttải vềDữ liệu sâu cần được tải xuống bằng API trong danh sách trắng hoặc bạn có thể tự thu thập dữ liệu. Đối với mục đích kiểm tra ngược, bạn chỉ có thể sử dụng dữ liệu giao dịch đã thu thập. Bài viết này lấy dữ liệu của HOOKUSDT-aggTrades-2023-01-27 làm ví dụ.
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
Các cột của một giao dịch như sau:
- agg_trade_id: id của lệnh giao dịch tổng hợp,
- Giá: giá giao dịch
- Số lượng: Số lượng giao dịch
- first_trade_id: Có thể có nhiều giao dịch trong bộ sưu tập cùng một lúc, chỉ có một dữ liệu được tính, đây là id của giao dịch đầu tiên
- last_trade_id: id của giao dịch cuối cùng
- transact_time: thời gian giao dịch
- is_buyer_maker: hướng giao dịch, True nghĩa là lệnh mua được giao dịch bởi người tạo lệnh và lệnh bán được giao dịch bởi người nhận lệnh
Có thể thấy rằng có 660.000 dữ liệu giao dịch vào ngày hôm đó và các giao dịch diễn ra rất sôi động. Tệp csv sẽ được đính kèm trong phần bình luận.
trades = pd.read_csv('COMPUSDT-aggTrades-2023-07-02.csv')
trades
664475 rows × 7 columns
| agg_trade_id | price | quantity | first_trade_id | last_trade_id | transact_time | is_buyer_maker |
|---|---|---|---|---|---|---|
| 120719552 | 52.42 | 22.087 | 207862988 | 207862990 | 1688256004603 | False |
| 120719553 | 52.41 | 29.314 | 207862991 | 207863002 | 1688256004623 | True |
| 120719554 | 52.42 | 0.945 | 207863003 | 207863003 | 1688256004678 | False |
| 120719555 | 52.41 | 13.534 | 207863004 | 207863006 | 1688256004680 | True |
| … | … | … | … | … | … | … |
| 121384024 | 68.29 | 10.065 | 210364899 | 210364905 | 1688342399863 | False |
| 121384025 | 68.30 | 7.078 | 210364906 | 210364908 | 1688342399948 | False |
| 121384026 | 68.29 | 7.622 | 210364909 | 210364911 | 1688342399979 | True |
Mô hình khối lượng giao dịch đơn lẻ
Đầu tiên, xử lý dữ liệu và chia các giao dịch ban đầu thành nhóm giao dịch đang hoạt động của lệnh mua và nhóm giao dịch đang hoạt động của lệnh bán. Ngoài ra, dữ liệu giao dịch tổng hợp ban đầu là một phần dữ liệu cùng lúc, cùng giá và cùng hướng. Có thể có lệnh mua đang hoạt động là 100. Nếu nó được chia thành nhiều giao dịch với giá khác nhau, chẳng hạn với 60 và 40, hai dữ liệu sẽ được tạo ra, ảnh hưởng đến việc ước tính khối lượng lệnh mua. Do đó, cần phải tổng hợp lại dựa trên transact_time. Sau khi tổng hợp, lượng dữ liệu đã giảm đi 140.000 bản ghi.
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
sell_trades = trades[trades['is_buyer_maker']==True].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
sell_trades = sell_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
sell_trades['interval']=sell_trades['transact_time'] - sell_trades['transact_time'].shift()
print(trades.shape[0] - (buy_trades.shape[0]+sell_trades.shape[0]))
146181
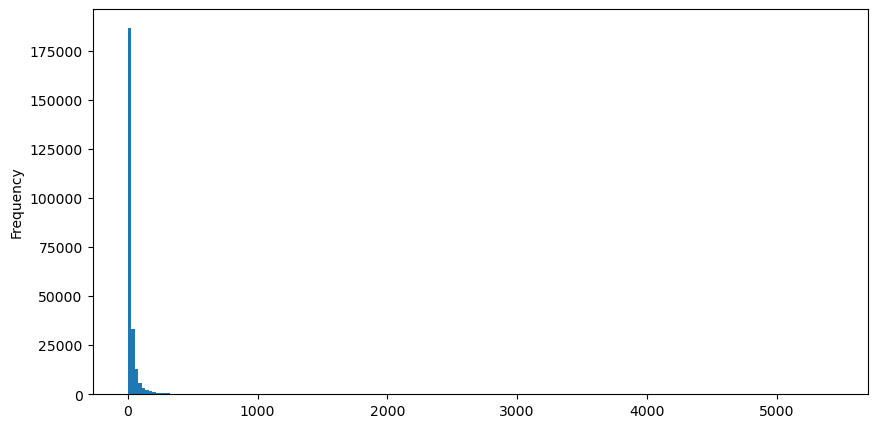
Lấy lệnh mua làm ví dụ, trước tiên hãy vẽ một biểu đồ histogram. Bạn có thể thấy hiệu ứng đuôi dài rất rõ ràng. Hầu hết dữ liệu tập trung ở phía bên trái, nhưng cũng có một số ít giao dịch lớn phân bổ ở phía đuôi .
buy_trades['quantity'].plot.hist(bins=200,figsize=(10, 5));
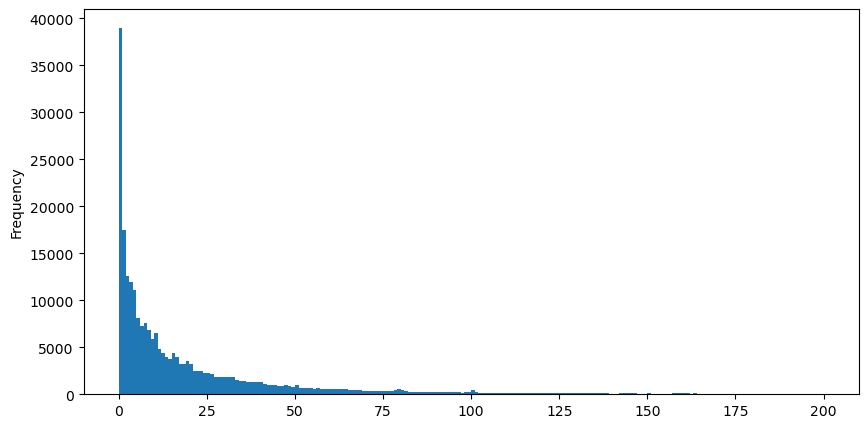
Để thuận tiện cho việc quan sát, chúng ta cắt đuôi và quan sát. Ta có thể thấy rằng khối lượng giao dịch càng lớn thì tần suất xuất hiện càng thấp và xu hướng giảm càng nhanh.
buy_trades['quantity'][buy_trades['quantity']<200].plot.hist(bins=200,figsize=(10, 5));
Có nhiều nghiên cứu về sự phân bố mức độ hài lòng về khối lượng. Phân phối lũy thừa của nó còn được gọi là phân phối Pareto, đây là một dạng phân phối xác suất phổ biến trong vật lý thống kê và khoa học xã hội. Trong phân phối theo luật lũy thừa, xác suất của một sự kiện có quy mô (hoặc tần suất) nhất định tỷ lệ thuận với một số mũ âm của quy mô của sự kiện đó. Đặc điểm chính của dạng phân phối này là các sự kiện lớn (tức là các sự kiện cách xa giá trị trung bình) xảy ra thường xuyên hơn so với dự kiến trong nhiều dạng phân phối khác. Đây là đặc điểm của phân phối khối lượng giao dịch. Dạng phân phối Pareto là: P(x) = Cx^(-α). Điều này sẽ được chứng minh dưới đây.
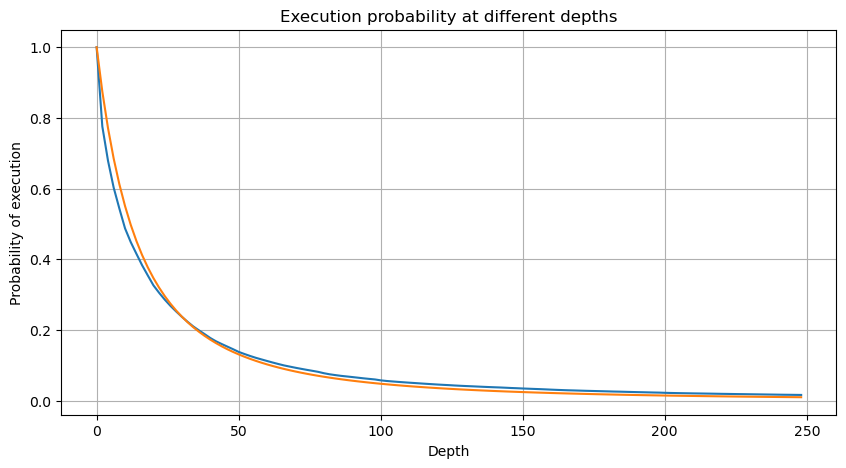
Hình bên dưới cho thấy xác suất khối lượng giao dịch lớn hơn một giá trị nhất định. Đường màu xanh là xác suất thực tế và đường màu cam là xác suất mô phỏng. Đừng lo lắng về các thông số cụ thể ở đây. Bạn có thể thấy rằng nó thỏa mãn phân phối Pareto. Vì xác suất khối lượng đơn hàng lớn hơn 0 là 1 và để đáp ứng các yêu cầu chuẩn hóa, phương trình phân phối phải như sau:
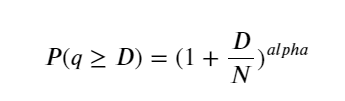
Trong đó N là tham số chuẩn hóa. Ở đây chúng tôi chọn thể tích trung bình M và alpha -2,06. Ước tính cụ thể của alpha có thể được tính toán bằng cách tính ngược giá trị P khi D = N. Cụ thể: alpha = log(P(d>M))/log(2) . Việc chọn các điểm khác nhau sẽ dẫn đến các giá trị alpha khác nhau đôi chút.
depths = range(0, 250, 2)
probabilities = np.array([np.mean(buy_trades['quantity'] > depth) for depth in depths])
alpha = np.log(np.mean(buy_trades['quantity'] > mean_quantity))/np.log(2)
mean_quantity = buy_trades['quantity'].mean()
probabilities_s = np.array([(1+depth/mean_quantity)**alpha for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
plt.figure(figsize=(10, 5))
plt.grid(True)
plt.title('Diff')
plt.plot(depths, probabilities_s-probabilities);
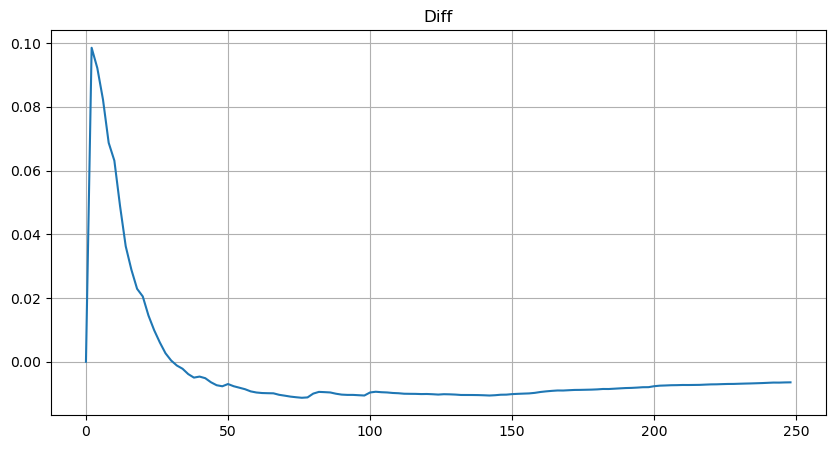
Nhưng ước tính này chỉ có vẻ như vậy. Trong hình trên, chúng tôi vẽ biểu đồ sự khác biệt giữa giá trị mô phỏng và giá trị thực tế. Khi khối lượng giao dịch nhỏ, độ lệch sẽ lớn, thậm chí gần 10%. Xác suất của một điểm có thể chính xác hơn bằng cách chọn các điểm khác nhau trong quá trình ước tính tham số, nhưng điều này không giải quyết được vấn đề độ lệch. Điều này được xác định bởi sự khác biệt giữa phân phối lũy thừa và phân phối thực tế. Để có được kết quả chính xác hơn, cần phải hiệu chỉnh phương trình phân phối lũy thừa. Tôi sẽ không đi sâu vào chi tiết về quy trình cụ thể, nhưng tôi chợt nảy ra ý tưởng và thấy rằng quy trình thực sự phải như sau:
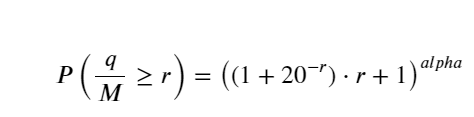
Để đơn giản, r = q/M được sử dụng ở đây để biểu diễn khối lượng giao dịch chuẩn hóa. Các tham số có thể được ước tính theo cách tương tự như trên. Hình bên dưới cho thấy độ lệch tối đa sau khi hiệu chỉnh không vượt quá 2%. Về mặt lý thuyết, có thể tiếp tục hiệu chỉnh, nhưng độ chính xác này là đủ.
depths = range(0, 250, 2)
probabilities = np.array([np.mean(buy_trades['quantity'] > depth) for depth in depths])
mean = buy_trades['quantity'].mean()
alpha = np.log(np.mean(buy_trades['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([(((1+20**(-depth/mean))*depth+mean)/mean)**alpha for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
plt.figure(figsize=(10, 5))
plt.grid(True)
plt.title('Diff')
plt.plot(depths, probabilities_s-probabilities);
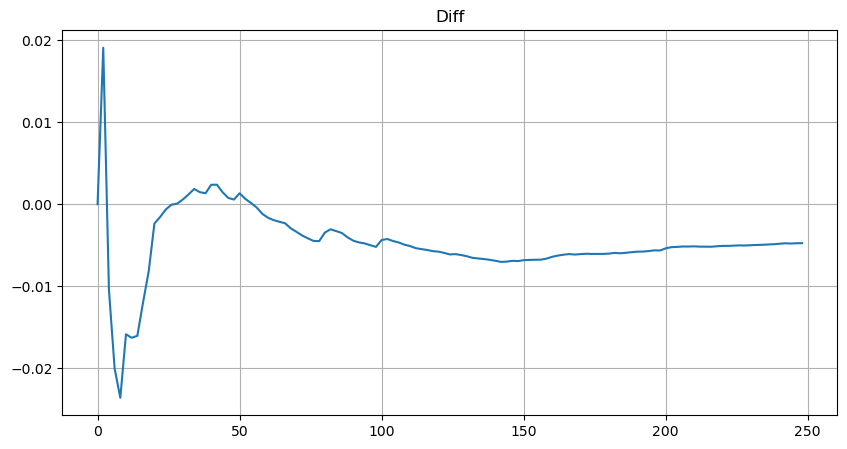
Với phương trình ước tính về phân phối thể tích, lưu ý rằng xác suất của phương trình không phải là xác suất thực mà là xác suất có điều kiện. Tại thời điểm này, chúng ta có thể trả lời câu hỏi này: nếu lệnh tiếp theo xảy ra, thì xác suất lệnh này lớn hơn một giá trị nhất định là bao nhiêu? Nói cách khác, xác suất thực hiện các lệnh có độ sâu khác nhau (tình huống lý tưởng, không quá khắt khe, về mặt lý thuyết, sổ lệnh có các lệnh mới và lệnh hủy, cũng như các hàng đợi ở cùng độ sâu) là bao nhiêu?
Bài viết đã gần hoàn thành ở đây, và vẫn còn nhiều câu hỏi cần được giải đáp. Loạt bài viết sau sẽ cố gắng cung cấp câu trả lời.