Suy nghĩ về các chiến lược giao dịch tần suất cao (2)
 1
1
 3416
3416
Bài viết chủ yếu thảo luận về các chiến lược giao dịch tần suất cao, tập trung vào mô hình khối lượng tích lũy và cú sốc giá. Bài báo này đề xuất một mô hình sắp xếp lệnh tối ưu sơ bộ bằng cách phân tích tác động của các giao dịch đơn lẻ, cú sốc giá theo khoảng thời gian cố định và khối lượng giao dịch lên giá. Mô hình này cố gắng tìm ra vị thế giao dịch tối ưu dựa trên sự hiểu biết về cú sốc về khối lượng và giá. Các giả định của mô hình được thảo luận sâu rộng và đánh giá sơ bộ về vị trí đặt hàng tối ưu được thực hiện bằng cách so sánh lợi nhuận thực tế và lợi nhuận dự kiến theo mô hình.
Mô hình khối lượng tích lũy
Bài viết trước đã đưa ra biểu thức xác suất cho một khối lượng giao dịch duy nhất lớn hơn một giá trị nhất định:
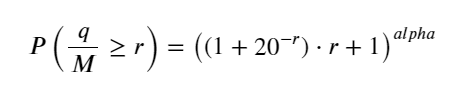
Chúng tôi cũng quan tâm đến sự phân bổ khối lượng giao dịch trong một khoảng thời gian, trực quan mà nói thì điều này liên quan đến khối lượng của mỗi giao dịch và tần suất đặt lệnh. Tiếp theo, dữ liệu được xử lý theo những khoảng thời gian cố định. Vẽ đồ thị phân phối của nó như trên.
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
trades = pd.read_csv('HOOKUSDT-aggTrades-2023-01-27.csv')
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
buy_trades.index = buy_trades['date']
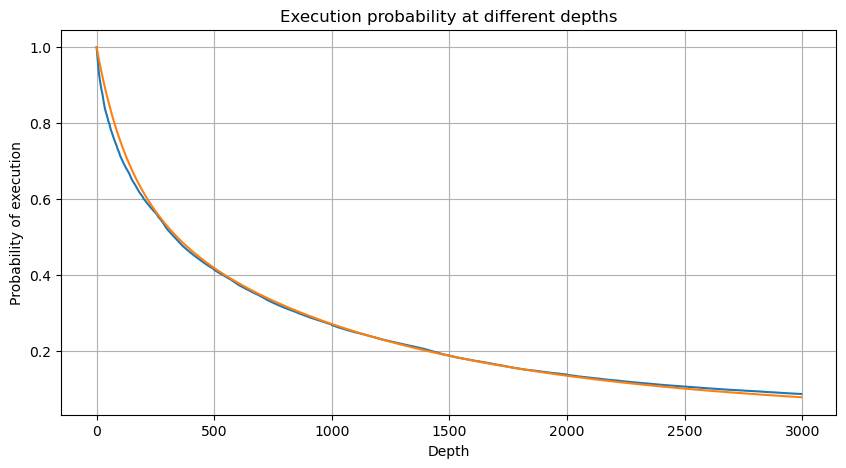
Hợp nhất khối lượng giao dịch sau mỗi 1 giây, loại bỏ phần không có giao dịch nào xảy ra và sử dụng phân phối của giao dịch đơn lẻ ở trên để phù hợp. Có thể thấy rằng kết quả tốt hơn. Nếu tất cả các giao dịch trong vòng 1 giây được coi là các giao dịch đơn lẻ, vấn đề này trở thành Đây đã trở thành một vấn đề được giải quyết. Tuy nhiên, khi chu kỳ kéo dài (so với tần suất giao dịch), lỗi sẽ tăng lên và nghiên cứu đã phát hiện ra rằng lỗi này là do điều khoản hiệu chỉnh phân phối Pareto trước đó gây ra. Điều này có nghĩa là khi chu kỳ kéo dài và bao gồm nhiều giao dịch riêng lẻ hơn, sự kết hợp của nhiều giao dịch sẽ tiến gần đến phân phối Pareto. Trong trường hợp này, cần loại bỏ thuật ngữ hiệu chỉnh.
df_resampled = buy_trades['quantity'].resample('1S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
buy_trades
| agg_trade_id | price | quantity | first_trade_id | last_trade_id | is_buyer_maker | date | transact_time | interval | diff | |
|---|---|---|---|---|---|---|---|---|---|---|
| 2023-01-27 00:00:00.161 | 1138369 | 2.901 | 54.3 | 3806199 | 3806201 | False | 2023-01-27 00:00:00.161 | 1674777600161 | NaN | 0.001 |
| 2023-01-27 00:00:04.140 | 1138370 | 2.901 | 291.3 | 3806202 | 3806203 | False | 2023-01-27 00:00:04.140 | 1674777604140 | 3979.0 | 0.000 |
| 2023-01-27 00:00:04.339 | 1138373 | 2.902 | 55.1 | 3806205 | 3806207 | False | 2023-01-27 00:00:04.339 | 1674777604339 | 199.0 | 0.001 |
| 2023-01-27 00:00:04.772 | 1138374 | 2.902 | 1032.7 | 3806208 | 3806223 | False | 2023-01-27 00:00:04.772 | 1674777604772 | 433.0 | 0.000 |
| 2023-01-27 00:00:05.562 | 1138375 | 2.901 | 3.5 | 3806224 | 3806224 | False | 2023-01-27 00:00:05.562 | 1674777605562 | 790.0 | 0.000 |
| … | … | … | … | … | … | … | … | … | … | … |
| 2023-01-27 23:59:57.739 | 1544370 | 3.572 | 394.8 | 5074645 | 5074651 | False | 2023-01-27 23:59:57.739 | 1674863997739 | 1224.0 | 0.002 |
| 2023-01-27 23:59:57.902 | 1544372 | 3.573 | 177.6 | 5074652 | 5074655 | False | 2023-01-27 23:59:57.902 | 1674863997902 | 163.0 | 0.001 |
| 2023-01-27 23:59:58.107 | 1544373 | 3.573 | 139.8 | 5074656 | 5074656 | False | 2023-01-27 23:59:58.107 | 1674863998107 | 205.0 | 0.000 |
| 2023-01-27 23:59:58.302 | 1544374 | 3.573 | 60.5 | 5074657 | 5074657 | False | 2023-01-27 23:59:58.302 | 1674863998302 | 195.0 | 0.000 |
| 2023-01-27 23:59:59.894 | 1544376 | 3.571 | 12.1 | 5074662 | 5074664 | False | 2023-01-27 23:59:59.894 | 1674863999894 | 1592.0 | 0.000 |
#1s内的累计分布
depths = np.array(range(0, 3000, 5))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
df_resampled = buy_trades['quantity'].resample('30S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
depths = np.array(range(0, 12000, 20))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2)
probabilities_s_2 = np.array([(depth/mean+1)**alpha for depth in depths]) # 无修正
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities,label='Probabilities (True)')
plt.plot(depths, probabilities_s, label='Probabilities (Simulation 1)')
plt.plot(depths, probabilities_s_2, label='Probabilities (Simulation 2)')
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.legend()
plt.grid(True)
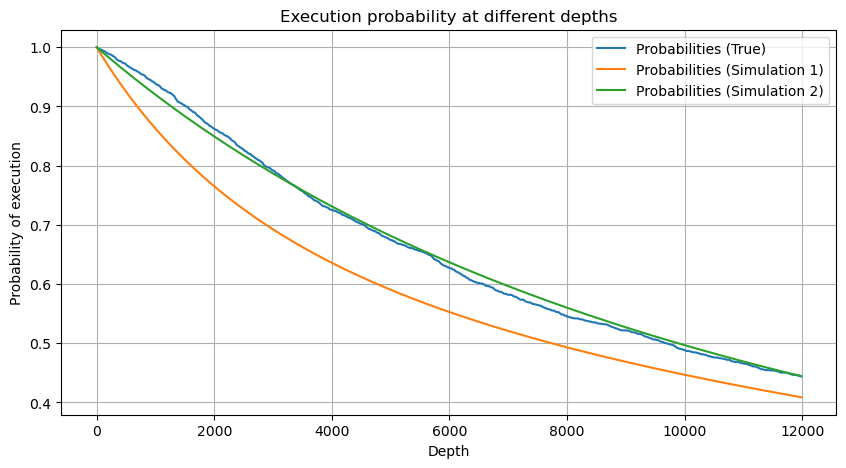
Bây giờ chúng tôi đã tóm tắt công thức chung về phân phối khối lượng giao dịch tích lũy tại các thời điểm khác nhau và sử dụng phân phối của các giao dịch riêng lẻ để phù hợp với công thức này mà không cần phải tính riêng từng giao dịch một. Ở đây chúng ta bỏ qua quá trình này và đưa ra công thức trực tiếp:
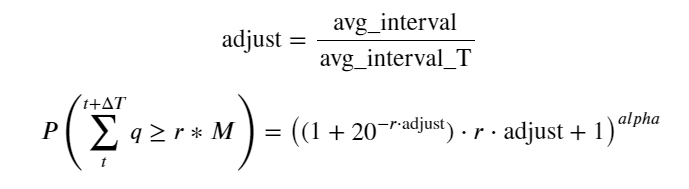
Trong số đó, avg_interval biểu thị khoảng thời gian trung bình giữa các giao dịch đơn lẻ và avg_interval_T biểu thị khoảng thời gian trung bình của các khoảng thời gian cần ước tính. Điều này hơi khó hiểu. Nếu chúng ta muốn ước tính thời gian giao dịch là 1 giây, chúng ta cần tính toán khoảng thời gian trung bình giữa các sự kiện chứa giao dịch trong vòng 1 giây. Nếu xác suất đơn hàng đến tuân theo phân phối Poisson, chúng ta có thể ước tính trực tiếp tại đây, nhưng độ lệch thực tế lại lớn nên chúng tôi sẽ không giải thích ở đây.
Lưu ý rằng xác suất khối lượng lớn hơn một giá trị nhất định trong một khoảng thời gian nhất định phải khá khác so với xác suất thực tế của giao dịch tại vị trí đó trong độ sâu, vì thời gian chờ càng dài thì khả năng sổ lệnh càng lớn. thay đổi và giao dịch cũng dẫn đến Độ sâu thay đổi, do đó xác suất giao dịch ở cùng vị trí độ sâu thay đổi theo thời gian thực khi dữ liệu được cập nhật.
df_resampled = buy_trades['quantity'].resample('2S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
depths = np.array(range(0, 6500, 10))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = buy_trades['quantity'].mean()
adjust = buy_trades['interval'].mean() / 2620
alpha = np.log(np.mean(buy_trades['quantity'] > mean))/0.7178397931503168
probabilities_s = np.array([((1+20**(-depth*adjust/mean))*depth*adjust/mean+1)**(alpha) for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
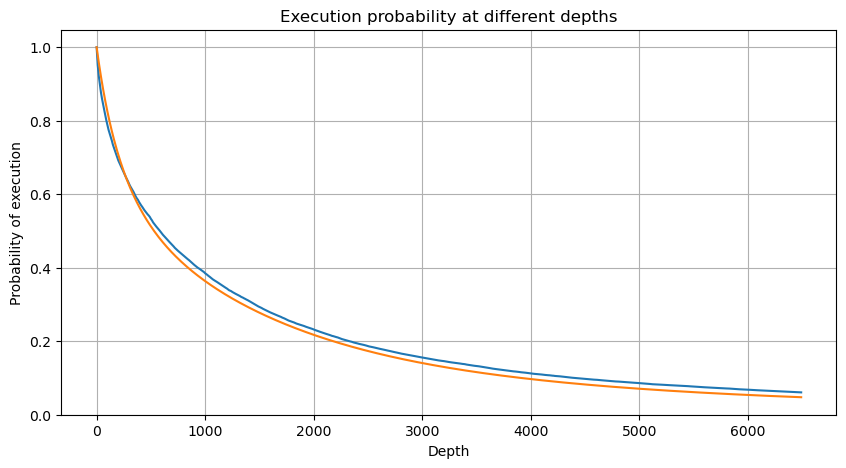
Tác động giá của giao dịch đơn lẻ
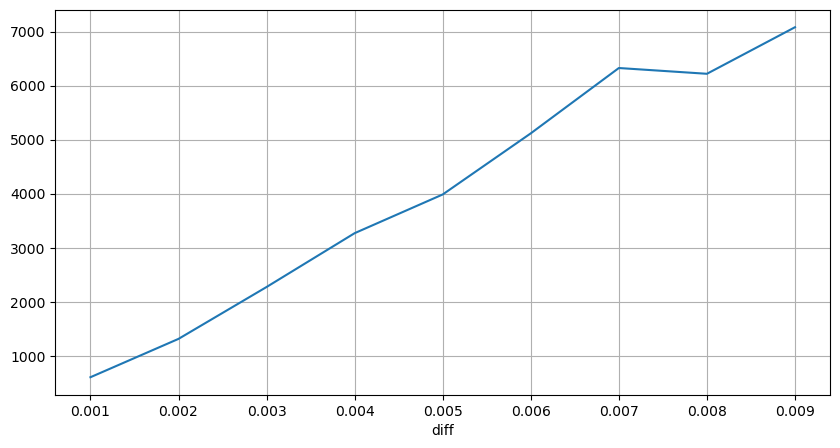
Dữ liệu giao dịch là một kho báu và vẫn còn rất nhiều dữ liệu cần được khai thác. Chúng ta nên chú ý đến tác động của lệnh lên giá, điều này ảnh hưởng đến việc đặt lệnh chờ trong chiến lược. Tương tự, dựa trên dữ liệu tổng hợp transact_time, hãy tính toán sự khác biệt giữa giá cuối cùng và giá đầu tiên. Nếu chỉ có một lệnh, sự khác biệt là 0. Điều kỳ lạ là vẫn còn một số ít kết quả dữ liệu có kết quả âm. Đây hẳn là vấn đề về thứ tự sắp xếp dữ liệu, vì vậy tôi sẽ không đề cập ở đây.
Kết quả cho thấy tỷ lệ không tác động cao tới 77%, tỷ lệ 1 tick là 16,5%, 2 tick là 3,7%, 3 tick là 1,2% và tỷ lệ trên 4 tick là dưới 1%. . Về cơ bản, điều này phù hợp với đặc điểm của hàm mũ, nhưng cách điều chỉnh này không chính xác.
Khối lượng giao dịch gây ra chênh lệch giá tương ứng đã được tính toán và sự biến dạng do tác động quá lớn đã được loại bỏ. Về cơ bản, nó tuân thủ mối quan hệ tuyến tính và cứ khoảng 1.000 khối lượng sẽ gây ra biến động giá 1 tick. Cũng có thể hiểu rằng số lượng lệnh chờ trung bình gần mỗi mức giá là khoảng 1.000.
diff_df = trades[trades['is_buyer_maker']==False].groupby('transact_time')['price'].agg(lambda x: abs(round(x.iloc[-1] - x.iloc[0],3)) if len(x) > 1 else 0)
buy_trades['diff'] = buy_trades['transact_time'].map(diff_df)
diff_counts = buy_trades['diff'].value_counts()
diff_counts[diff_counts>10]/diff_counts.sum()
0.000 0.769965
0.001 0.165527
0.002 0.037826
0.003 0.012546
0.004 0.005986
0.005 0.003173
0.006 0.001964
0.007 0.001036
0.008 0.000795
0.009 0.000474
0.010 0.000227
0.011 0.000187
0.012 0.000087
0.013 0.000080
Name: diff, dtype: float64
diff_group = buy_trades.groupby('diff').agg({
'quantity': 'mean',
'diff': 'last',
})
diff_group['quantity'][diff_group['diff']>0][diff_group['diff']<0.01].plot(figsize=(10,5),grid=True);
Giá sốc ở các khoảng thời gian đều đặn
Đếm tác động giá trong vòng 2 giây. Sự khác biệt ở đây là sẽ có giá trị âm. Tất nhiên, vì chỉ có lệnh mua được tính ở đây, nên vị thế đối xứng sẽ lớn hơn một tick. Tiếp tục quan sát mối quan hệ giữa khối lượng giao dịch và tác động, và chỉ tính các kết quả lớn hơn 0. Kết luận tương tự như kết luận của một lệnh đơn, cũng là mối quan hệ tuyến tính gần đúng. Mỗi tích tắc cần khoảng 2000 khối lượng.
df_resampled = buy_trades.resample('2S').agg({
'price': ['first', 'last', 'count'],
'quantity': 'sum'
})
df_resampled['price_diff'] = round(df_resampled[('price', 'last')] - df_resampled[('price', 'first')],3)
df_resampled['price_diff'] = df_resampled['price_diff'].fillna(0)
result_df_raw = pd.DataFrame({
'price_diff': df_resampled['price_diff'],
'quantity_sum': df_resampled[('quantity', 'sum')],
'data_count': df_resampled[('price', 'count')]
})
result_df = result_df_raw[result_df_raw['price_diff'] != 0]
result_df['price_diff'][abs(result_df['price_diff'])<0.016].value_counts().sort_index().plot.bar(figsize=(10,5));
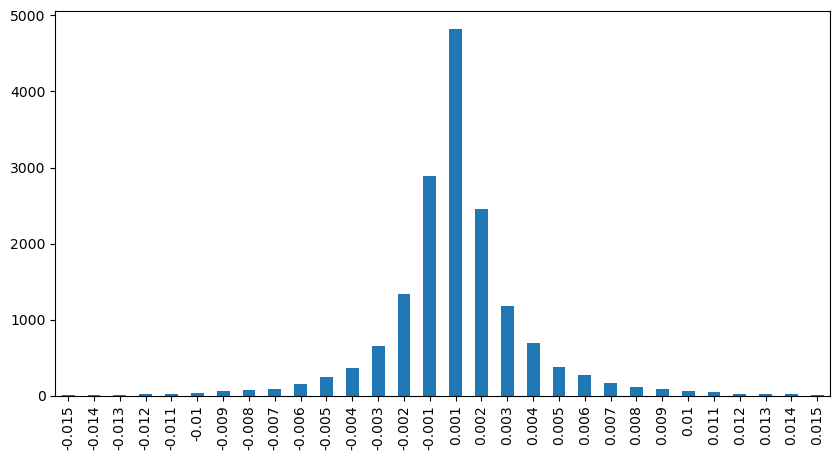
result_df['price_diff'].value_counts()[result_df['price_diff'].value_counts()>30]
0.001 7176
-0.001 3665
0.002 3069
-0.002 1536
0.003 1260
0.004 692
-0.003 608
0.005 391
-0.004 322
0.006 259
-0.005 192
0.007 146
-0.006 112
0.008 82
0.009 75
-0.007 75
-0.008 65
0.010 51
0.011 41
-0.010 31
Name: price_diff, dtype: int64
diff_group = result_df.groupby('price_diff').agg({ 'quantity_sum': 'mean'})
diff_group[(diff_group.index>0) & (diff_group.index<0.015)].plot(figsize=(10,5),grid=True);
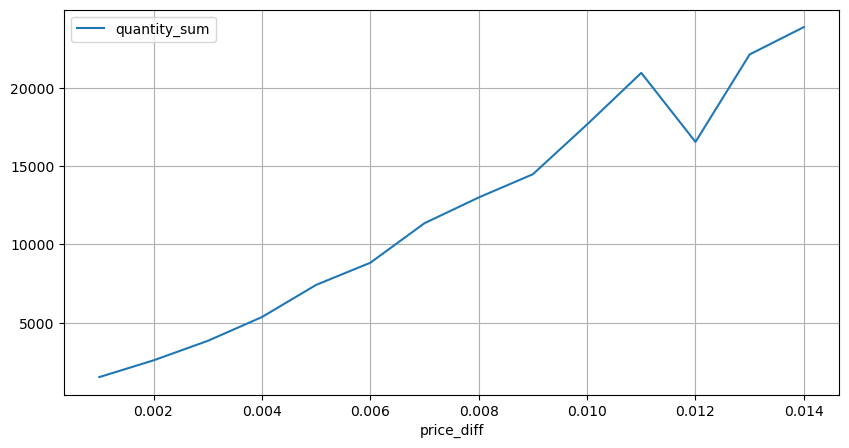
Tác động của giá cả đến khối lượng
Thể tích cần thiết cho một thay đổi tích tắc đã được tính toán trước đó, nhưng nó không chính xác vì nó dựa trên giả định rằng tác động đã xảy ra. Bây giờ chúng ta hãy xem xét tác động của khối lượng giao dịch đến giá.
Dữ liệu ở đây được lấy mẫu trong 1 giây, với 100 số lượng là 1 bước và những thay đổi về giá trong phạm vi số lượng này sẽ được tính. Một số kết luận có giá trị đã được rút ra:
- Khi khối lượng mua dưới 500, mức giá dự kiến sẽ giảm, điều này là bình thường vì cũng có lệnh bán ảnh hưởng đến giá.
- Khi khối lượng giao dịch thấp, nó tuân theo mối quan hệ tuyến tính, nghĩa là khối lượng giao dịch càng lớn thì mức tăng giá càng lớn.
- Khối lượng lệnh mua càng lớn thì giá thay đổi càng lớn, thường biểu thị sự đột phá về giá. Sau khi đột phá, giá có thể quay trở lại. Kết hợp với việc lấy mẫu theo các khoảng thời gian cố định, dữ liệu không ổn định.
- Cần chú ý đến phần trên của biểu đồ phân tán, tức là phần mà khối lượng tương ứng với mức tăng giá.
- Chỉ đối với cặp giao dịch này, phiên bản sơ bộ về mối quan hệ giữa khối lượng và thay đổi giá được đưa ra:
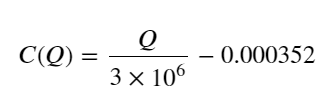
Trong đó, “C” biểu thị sự thay đổi về giá và “Q” biểu thị khối lượng lệnh mua.
df_resampled = buy_trades.resample('1S').agg({
'price': ['first', 'last', 'count'],
'quantity': 'sum'
})
df_resampled['price_diff'] = round(df_resampled[('price', 'last')] - df_resampled[('price', 'first')],3)
df_resampled['price_diff'] = df_resampled['price_diff'].fillna(0)
result_df_raw = pd.DataFrame({
'price_diff': df_resampled['price_diff'],
'quantity_sum': df_resampled[('quantity', 'sum')],
'data_count': df_resampled[('price', 'count')]
})
result_df = result_df_raw[result_df_raw['price_diff'] != 0]
df = result_df.copy()
bins = np.arange(0, 30000, 100) #
labels = [f'{i}-{i+100-1}' for i in bins[:-1]]
df.loc[:, 'quantity_group'] = pd.cut(df['quantity_sum'], bins=bins, labels=labels)
grouped = df.groupby('quantity_group')['price_diff'].mean()
grouped_df = pd.DataFrame(grouped).reset_index()
grouped_df['quantity_group_center'] = grouped_df['quantity_group'].apply(lambda x: (float(x.split('-')[0]) + float(x.split('-')[1])) / 2)
plt.figure(figsize=(10,5))
plt.scatter(grouped_df['quantity_group_center'], grouped_df['price_diff'],s=10)
plt.plot(grouped_df['quantity_group_center'], np.array(grouped_df['quantity_group_center'].values)/2e6-0.000352,color='red')
plt.xlabel('quantity_group_center')
plt.ylabel('average price_diff')
plt.title('Scatter plot of average price_diff by quantity_group')
plt.grid(True)
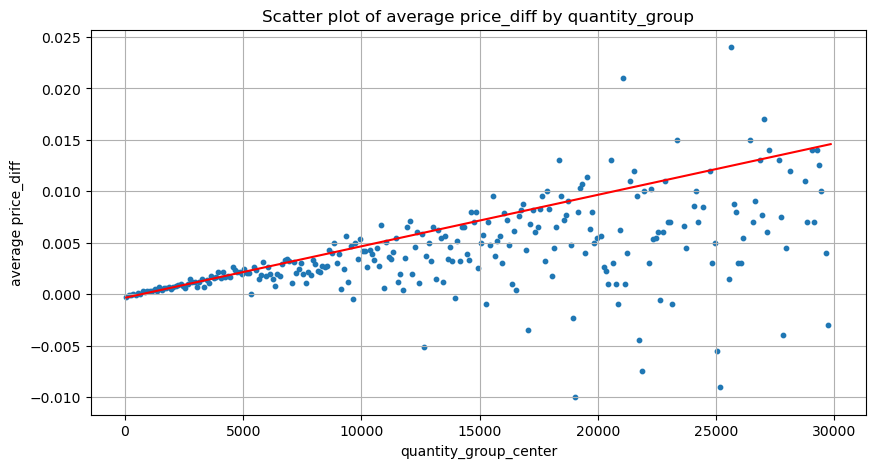
grouped_df.head(10)
| quantity_group | price_diff | quantity_group_center | |
|---|---|---|---|
| 0 | 0-199 | -0.000302 | 99.5 |
| 1 | 100-299 | -0.000124 | 199.5 |
| 2 | 200-399 | -0.000068 | 299.5 |
| 3 | 300-499 | -0.000017 | 399.5 |
| 4 | 400-599 | -0.000048 | 499.5 |
| 5 | 500-699 | 0.000098 | 599.5 |
| 6 | 600-799 | 0.000006 | 699.5 |
| 7 | 700-899 | 0.000261 | 799.5 |
| 8 | 800-999 | 0.000186 | 899.5 |
| 9 | 900-1099 | 0.000299 | 999.5 |
Vị trí thứ tự tối ưu ban đầu
Với mô hình khối lượng giao dịch và mô hình sơ bộ về khối lượng giao dịch tương ứng với tác động giá, có vẻ như có thể tính toán được vị thế đặt lệnh tối ưu. Hãy đưa ra một số giả định và đưa ra mức giá tối ưu không chịu trách nhiệm.
- Giả sử giá trở lại giá trị ban đầu sau cú sốc (điều này tất nhiên là không thể xảy ra và đòi hỏi phải phân tích lại những thay đổi về giá sau cú sốc)
- Giả sử rằng sự phân bổ khối lượng giao dịch và tần suất đặt lệnh trong giai đoạn này đáp ứng các yêu cầu đặt trước (điều này cũng không chính xác vì giá trị của một ngày được sử dụng để ước tính và các giao dịch có sự phân nhóm rõ ràng).
- Giả sử chỉ có một lệnh bán xảy ra trong thời gian mô phỏng và sau đó vị thế được đóng lại.
- Giả sử rằng sau khi lệnh được thực hiện, có các lệnh mua khác tiếp tục đẩy giá lên, đặc biệt là khi khối lượng rất thấp. Hiệu ứng này bị bỏ qua ở đây và chỉ đơn giản là giả định rằng nó sẽ quay trở lại.
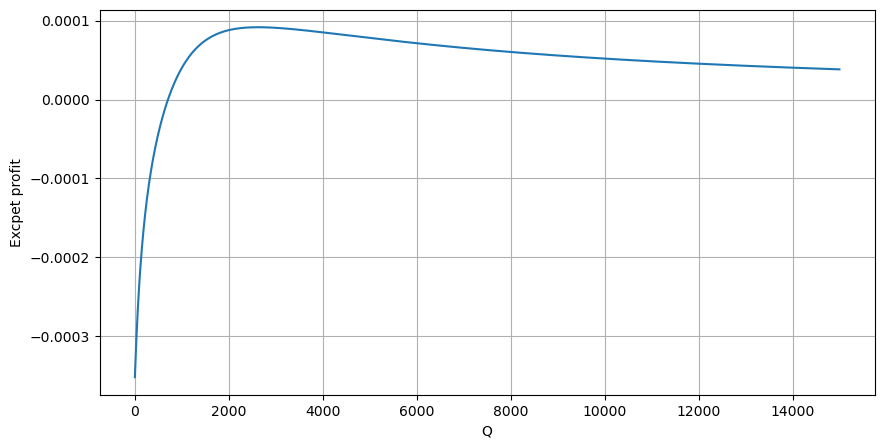
Đầu tiên, hãy viết ra một kỳ vọng lợi nhuận đơn giản, tức là xác suất lệnh mua tích lũy lớn hơn Q trong vòng 1 giây, nhân với tỷ lệ lợi nhuận kỳ vọng (tức là giá tác động):
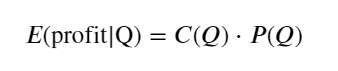
Theo biểu đồ, lợi nhuận dự kiến đạt mức tối đa vào khoảng 2500, gấp khoảng 2,5 lần khối lượng giao dịch trung bình. Nghĩa là, lệnh bán phải được đặt ở mức 2500. Cần nhấn mạnh lại rằng trục ngang biểu thị khối lượng giao dịch trong vòng 1 giây và không thể đơn giản coi nó tương đương với vị thế sâu. Và điều này xảy ra vào thời điểm vẫn còn thiếu dữ liệu chuyên sâu quan trọng và chỉ dựa trên suy đoán về giao dịch.
Tóm tắt
Người ta thấy rằng phân phối khối lượng tại các khoảng thời gian khác nhau là phép chia đơn giản cho phân phối khối lượng của một giao dịch duy nhất. Chúng tôi cũng đã tạo ra một mô hình lợi nhuận kỳ vọng đơn giản dựa trên các cú sốc giá và xác suất giao dịch. Kết quả của mô hình này phù hợp với kỳ vọng của chúng tôi. Nếu khối lượng lệnh bán nhỏ, điều đó cho thấy giá giảm. Cần phải có một số tiền nhất định để có lợi nhuận biên lợi nhuận, và khối lượng giao dịch càng lớn thì biên lợi nhuận càng cao. Xác suất càng lớn thì biên lợi nhuận càng thấp. Có một kích thước tối ưu ở giữa, đây cũng là vị trí đặt lệnh mà chiến lược đang tìm kiếm. Tất nhiên, mô hình này vẫn còn quá đơn giản. Trong bài viết tiếp theo, tôi sẽ tiếp tục thảo luận sâu hơn về nó.
#1s内的累计分布
df_resampled = buy_trades['quantity'].resample('1S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
depths = np.array(range(0, 15000, 10))
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])
profit_s = np.array([depth/2e6-0.000352 for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities_s*profit_s)
plt.xlabel('Q')
plt.ylabel('Excpet profit')
plt.grid(True)