Suy nghĩ về các chiến lược giao dịch tần suất cao (3)
 0
0
 2664
2664

Trong bài viết trước, tôi đã giới thiệu cách mô hình hóa khối lượng giao dịch tích lũy và phân tích ngắn gọn hiện tượng sốc giá. Bài viết này sẽ tiếp tục phân tích dữ liệu lệnh giao dịch. Trong hai ngày qua, YGG đã ra mắt hợp đồng dựa trên Binance U, giá cả biến động rất lớn, thậm chí có thời điểm khối lượng giao dịch còn vượt qua cả BTC. Chúng ta hãy cùng phân tích hôm nay.
Khoảng thời gian đặt hàng
Nhìn chung, người ta cho rằng thời gian khi đơn hàng đến tuân theo quy trình Poisson. Sau đây là bài viết giới thiệuQuá trình Poisson . Tôi sẽ trình bày điều này bên dưới.
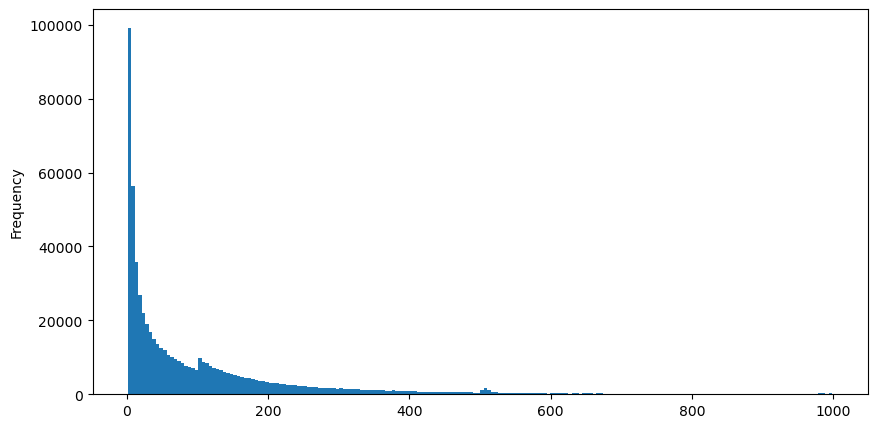
Tải xuống aggTrades vào ngày 5 tháng 8, tổng cộng có 1.931.193 giao dịch, con số này khá phóng đại. Trước tiên, hãy xem xét sự phân phối của các lệnh mua. Chúng ta có thể thấy rằng có một đỉnh cục bộ không đồng đều ở khoảng 100ms và 500ms. Điều này có thể là do các lệnh theo lịch trình được đặt bởi robot được Iceberg ủy thác. Đây cũng có thể là một về lý do tại sao điều kiện thị trường vào ngày hôm đó lại bất thường.
Hàm khối lượng xác suất (PMF) của phân phối Poisson được đưa ra bởi:
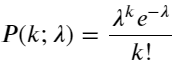
TRONG:
- k là số sự kiện mà chúng ta quan tâm.
- λ là tỷ lệ xảy ra trung bình của các sự kiện trên một đơn vị thời gian (hoặc đơn vị không gian).
- P(k; λ) là xác suất xảy ra đúng k sự kiện, với tỷ lệ xảy ra trung bình là λ.
Trong quá trình Poisson, khoảng thời gian giữa các sự kiện tuân theo phân phối mũ. Hàm mật độ xác suất (PDF) của phân phối mũ được đưa ra bởi:
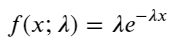
Thông qua việc điều chỉnh, người ta thấy rằng kết quả khá khác so với kết quả mong đợi của phân phối Poisson. Quá trình Poisson đánh giá thấp tần suất của các khoảng thời gian dài và đánh giá cao tần suất của các khoảng thời gian ngắn. (Phân phối khoảng thực tế gần hơn với phân phối Pareto đã sửa đổi)
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
trades = pd.read_csv('YGGUSDT-aggTrades-2023-08-05.csv')
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
buy_trades.index = buy_trades['date']
buy_trades['interval'][buy_trades['interval']<1000].plot.hist(bins=200,figsize=(10, 5));
Intervals = np.array(range(0, 1000, 5))
mean_intervals = buy_trades['interval'].mean()
buy_rates = 1000/mean_intervals
probabilities = np.array([np.mean(buy_trades['interval'] > interval) for interval in Intervals])
probabilities_s = np.array([np.e**(-buy_rates*interval/1000) for interval in Intervals])
plt.figure(figsize=(10, 5))
plt.plot(Intervals, probabilities)
plt.plot(Intervals, probabilities_s)
plt.xlabel('Intervals')
plt.ylabel('Probability')
plt.grid(True)
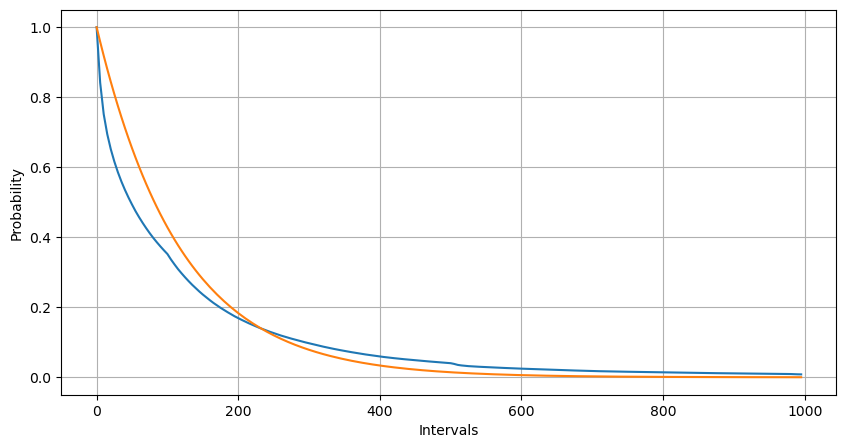
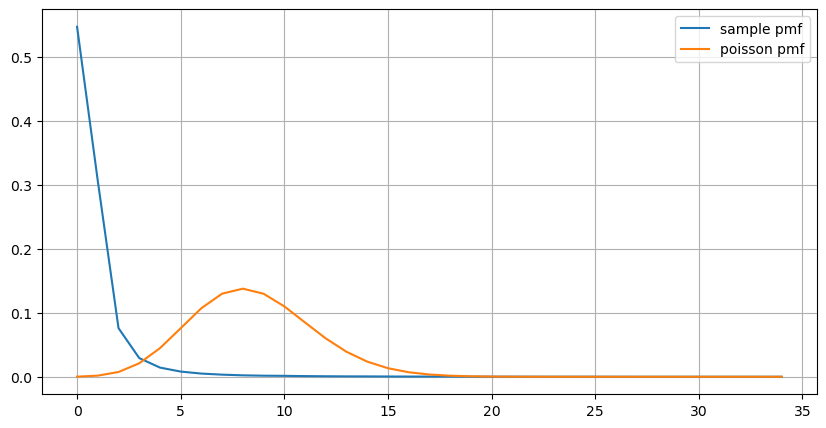
Phân phối thống kê số lượng lệnh xảy ra trong vòng 1 giây và so sánh với phân phối Poisson cũng cho thấy sự khác biệt rất rõ ràng. Phân phối Poisson đánh giá thấp đáng kể tần suất của các sự kiện có xác suất thấp. Nguyên nhân có thể:
- Tỷ lệ xảy ra không đổi: Quá trình Poisson giả định rằng tỷ lệ trung bình của các sự kiện xảy ra trong bất kỳ khoảng thời gian nào là không đổi. Nếu giả định này không đúng thì phân phối dữ liệu sẽ lệch khỏi phân phối Poisson.
- Tương tác của các tiến trình: Một giả định cơ bản khác của tiến trình Poisson là các sự kiện độc lập với nhau. Nếu các sự kiện trong thế giới thực ảnh hưởng lẫn nhau, phân phối của chúng có thể lệch khỏi phân phối Poisson.
Nghĩa là, trong môi trường thực tế, tần suất đặt hàng không phải là hằng số, cần được cập nhật theo thời gian thực và sẽ có các động cơ khuyến khích, tức là nhiều đơn hàng trong một thời gian cố định sẽ kích thích nhiều đơn hàng hơn. Điều này khiến việc sửa một tham số duy nhất trong chiến lược trở nên bất khả thi.
result_df = buy_trades.resample('0.1S').agg({
'price': 'count',
'quantity': 'sum'
}).rename(columns={'price': 'order_count', 'quantity': 'quantity_sum'})
count_df = result_df['order_count'].value_counts().sort_index()[result_df['order_count'].value_counts()>20]
(count_df/count_df.sum()).plot(figsize=(10,5),grid=True,label='sample pmf');
from scipy.stats import poisson
prob_values = poisson.pmf(count_df.index, 1000/mean_intervals)
plt.plot(count_df.index, prob_values,label='poisson pmf');
plt.legend() ;
Cập nhật thông số thời gian thực
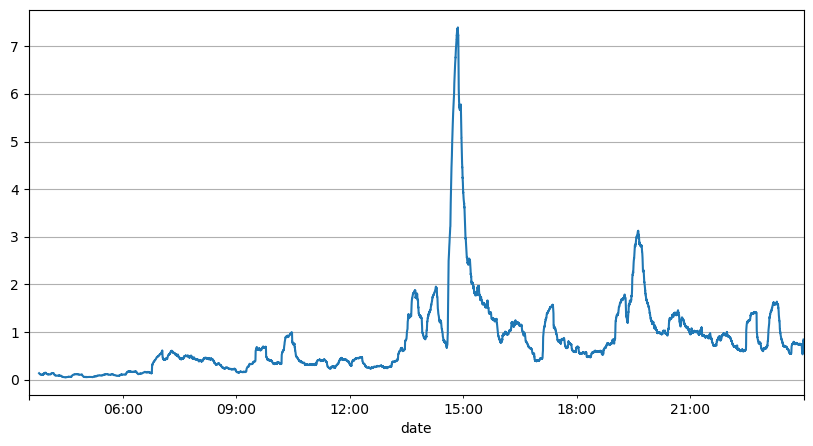
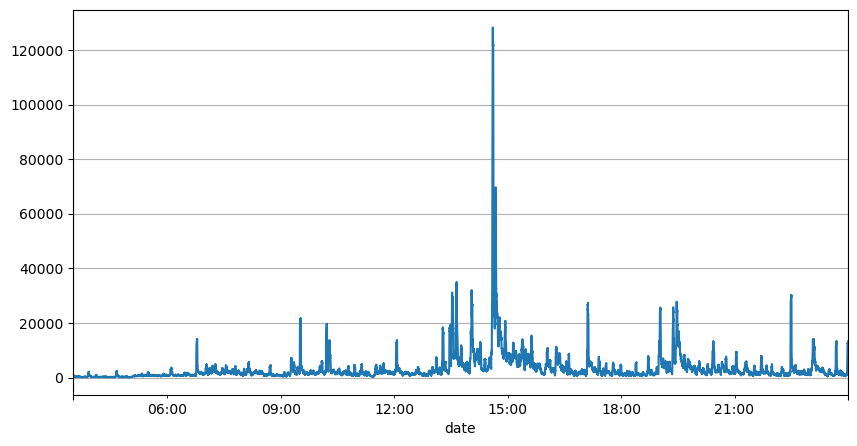
Phân tích trước đây về khoảng thời gian đặt hàng cho thấy các tham số cố định không phù hợp với điều kiện thị trường thực tế và các tham số chính của mô tả thị trường chiến lược cần được cập nhật theo thời gian thực. Giải pháp dễ nghĩ đến nhất là đường trung bình động của cửa sổ trượt. Hai con số dưới đây là tần suất lệnh mua trong vòng 1 giây và trung bình 1000 cửa sổ khối lượng giao dịch. Có thể thấy rằng có hiện tượng cụm trong các giao dịch, tức là tần suất lệnh cao hơn đáng kể so với bình thường đối với một trong một khoảng thời gian, và âm lượng tại thời điểm này cũng tăng lên đồng bộ. Ở đây, giá trị trung bình trước đó được sử dụng để dự đoán giá trị của giây gần nhất và sai số tuyệt đối trung bình của phần dư được sử dụng để đo lường chất lượng của dự đoán.
Từ biểu đồ, chúng ta cũng có thể hiểu tại sao tần suất lệnh lại lệch nhiều so với phân phối Poisson. Mặc dù số lệnh trung bình mỗi giây chỉ là 8,5 lần, nhưng trong những trường hợp cực đoan, số lệnh trung bình mỗi giây lại lệch xa so với nó.
Người ta nhận thấy rằng việc sử dụng giá trị trung bình của hai giây trước đó để dự đoán lỗi dư là nhỏ nhất và tốt hơn nhiều so với kết quả dự đoán giá trị trung bình đơn giản.
result_df['order_count'][::10].rolling(1000).mean().plot(figsize=(10,5),grid=True);
result_df
| order_count | quantity_sum | |
|---|---|---|
| 2023-08-05 03:30:06.100 | 1 | 76.0 |
| 2023-08-05 03:30:06.200 | 0 | 0.0 |
| 2023-08-05 03:30:06.300 | 0 | 0.0 |
| 2023-08-05 03:30:06.400 | 1 | 416.0 |
| 2023-08-05 03:30:06.500 | 0 | 0.0 |
| … | … | … |
| 2023-08-05 23:59:59.500 | 3 | 9238.0 |
| 2023-08-05 23:59:59.600 | 0 | 0.0 |
| 2023-08-05 23:59:59.700 | 1 | 3981.0 |
| 2023-08-05 23:59:59.800 | 0 | 0.0 |
| 2023-08-05 23:59:59.900 | 2 | 534.0 |
result_df['quantity_sum'].rolling(1000).mean().plot(figsize=(10,5),grid=True);
(result_df['order_count'] - result_df['mean_count'].mean()).abs().mean()
6.985628185332997
result_df['mean_count'] = result_df['order_count'].ewm(alpha=0.11, adjust=False).mean()
(result_df['order_count'] - result_df['mean_count'].shift()).abs().mean()
0.6727616961866929
result_df['mean_quantity'] = result_df['quantity_sum'].ewm(alpha=0.1, adjust=False).mean()
(result_df['quantity_sum'] - result_df['mean_quantity'].shift()).abs().mean()
4180.171479076811
Tóm tắt
Bài viết này giới thiệu tóm tắt lý do tại sao khoảng thời gian thứ tự lại khác với quá trình Poisson, chủ yếu là do các tham số thay đổi theo thời gian. Để dự đoán thị trường chính xác hơn, chiến lược cần đưa ra những dự đoán theo thời gian thực về các thông số cơ bản của thị trường. Có thể sử dụng phần dư để đo lường chất lượng dự đoán. Ví dụ trên là ví dụ đơn giản nhất. Có nhiều nghiên cứu liên quan về phân tích chuỗi thời gian, tổng hợp biến động, v.v., có thể được cải thiện thêm.