Chiến lược giao dịch hiệu quả phân cực Fractal (PFE)

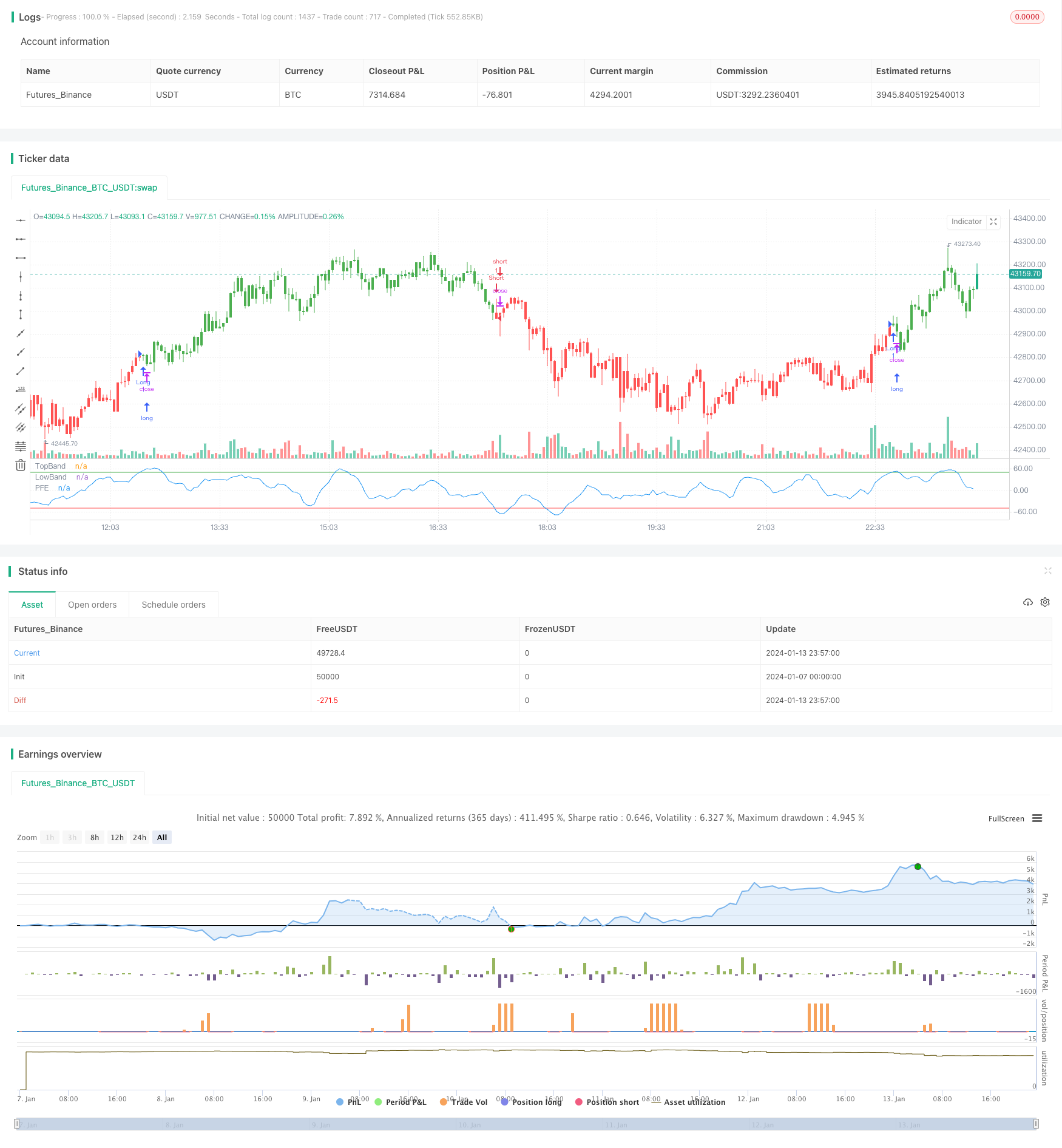
Tổng quan

Hiệu quả phân đoạn phân cực (Polarized Fractal Efficiency, PFE) là một chiến lược giao dịch đo lường hiệu quả của chuyển động giá bằng cách áp dụng các khái niệm về hình học phân đoạn và lý thuyết hỗn loạn. Phong trào giá là xuyên tuyến và hiệu quả, khoảng cách giữa hai điểm càng ngắn thì hiệu quả của chuyển động giá càng cao.

Nguyên tắc chiến lược

Chỉ số trung tâm của chiến lược giao dịch PFE là hiệu quả phân tách cực (PFE). Chỉ số này được tính dựa trên công thức sau:

PFE = sqrt(pow(close - close[Length], 2) + 100)

Trong đó, Length là khoảng thời gian cửa sổ xem lại, tham số này được đặt bằng cách nhập. PFE thực sự là thước đo chiều dài của giá trong thời gian Length, nó sử dụng khoảng cách Euclidean (đường thẳng) để đo gần.

Để đánh giá hiệu quả của chuyển động giá, chúng ta cần một chuẩn mực để so sánh. Mức chuẩn này là chiều dài của con đường giá kết nối theo thứ tự thực tế trong khoảng thời gian Length, được gọi là C2C ((Close to Close), và công thức tính toán như sau:

C2C = sum(sqrt(pow((close - close[1]), 2) + 1), Length)  

Vì vậy, chúng ta có thể tính toán hiệu quả phân dạng của biến động giá xFracEff:

xFracEff = iff(close - close[Length] > 0, round((PFE / C2C) * 100) , round(-(PFE / C2C) * 100))

Nếu giá tăng, điểm số là tích cực, nếu giảm, thì là âm. Giá trị tuyệt đối càng lớn, nghĩa là vận động càng kém hiệu quả.

Để tạo ra tín hiệu giao dịch, chúng tôi tính xEMA, tức là chỉ số di chuyển trung bình của xFracEff. Và thiết lập các kênh mua và bán:

xEMA = ema(xFracEff, LengthEMA) 

BuyBand = input(50)  
SellBand = input(-50)

Khi xEMA trên đi qua BuyBand tạo ra tín hiệu mua; khi xEMA dưới đi qua SellBand tạo ra tín hiệu bán.

Phân tích lợi thế

Chiến lược giao dịch PFE có những ưu điểm sau:

1. Sử dụng các phương pháp phân tách hình học và lý thuyết hỗn loạn độc đáo để đo lường hiệu quả của chuyển động giá từ một góc độ khác
2. Tránh xa một số vấn đề về chỉ số kỹ thuật thông thường, như phù hợp với đường cong
3. Có thể tìm các thiết lập phù hợp với các môi trường thị trường khác nhau bằng cách điều chỉnh các tham số
4. Các quy tắc giao dịch đơn giản, rõ ràng và dễ thực hiện

Phân tích rủi ro

Chiến lược giao dịch PFE cũng có những rủi ro sau:

1. Giống như tất cả các chiến lược chỉ số, tham số là khó để tối ưu hóa và dễ bị tối ưu hóa quá mức
2. Các tín hiệu mua và bán có thể không đáng tin cậy khi thị trường biến động mạnh
3. Cần thận trọng khi xử lý các mức cực đoan nếu giá đột ngột giảm
4. Cần phải chịu một khoảng thời gian chậm trễ, có thể đã bỏ lỡ điểm vào tốt nhất khi phát ra tín hiệu

Hướng tối ưu hóa

Chiến lược giao dịch PFE có thể được tối ưu hóa theo các khía cạnh sau:

1. Thử các kết hợp tham số Length khác nhau để tìm điểm cân bằng tốt nhất
2. Tối ưu hóa các tham số kênh mua bán để giảm khả năng giao dịch sai
3. Tham gia hệ thống ngăn chặn tổn thất, kiểm soát tổn thất đơn lẻ
4. Kết hợp với các chỉ số khác để cải thiện chất lượng tín hiệu
5. Động thái điều chỉnh tham số để thích ứng với sự thay đổi của môi trường thị trường

Tóm tắt

Chiến lược giao dịch PFE dựa trên hình học phân tách và lý thuyết hỗn độn, đưa ra một phương pháp mới để đo lường hiệu quả của chuyển động giá. So với các chỉ số kỹ thuật thông thường, phương pháp này có lợi thế riêng của nó, nhưng cũng phải đối mặt với một số vấn đề về độ trễ thời gian, tối ưu hóa tham số, chất lượng tín hiệu.