Chiến lược dự báo chuỗi thời gian AR-GARCH
Tại sao phân tích kỹ thuật truyền thống không hiệu quả trong thị trường phức tạp?
Trong lĩnh vực giao dịch định lượng, chúng ta thường gặp sự nhầm lẫn về lý do tại sao các chiến lược dựa trên đường trung bình di chuyển đơn giản hoặc RSI hoạt động tốt trong một số môi trường thị trường và thất bại thường xuyên trong các giai đoạn khác. Câu trả lời nằm ở sự phức tạp của các chuỗi thời gian tài chính - chúng không chỉ có liên quan đến bản thân mà còn có tính năng biến động theo thời gian.
Chiến lược mà chúng ta sẽ phân tích hôm nay, kết hợp một cách khéo léo mô hình AR(2) tự hồi quy và mô hình chênh lệch điều kiện GARCH(1,1) để cố gắng giải quyết vấn đề này từ góc độ thống kê. Đây không phải là chỉ số kỹ thuật đơn giản chồng lên nhau, mà là sự khai thác sâu sắc về các đặc điểm bản chất của chuỗi thời gian tài chính.
AR: 2) Mô hình này đã thu được hiệu ứng ký ức của giá như thế nào?
Đơn giản là sử dụng bản thân trong quá khứ để dự đoán bản thân trong tương lai. AR 2 giả định rằng tỷ lệ lợi nhuận hiện tại có thể được thể hiện tuyến tính bởi tỷ lệ lợi nhuận của hai giai đoạn trước:
r_t = φ₁ × r_{t-1} + φ₂ × r_{t-2} + ε_t
Mã giải các hệ số φ1 và φ2 bằng phương trình Yule-Walker:
c0 = calcAutoCovariance(returns, 0, lengthReg) // 滞后0期自协方差
c1 = calcAutoCovariance(returns, 1, lengthReg) // 滞后1期自协方差
c2 = calcAutoCovariance(returns, 2, lengthReg) // 滞后2期自协方差
phi1 = (c1 * c0 - c2 * c1) / denominator // 第一个自回归系数
phi2 = (c2 * c0 - c1 * c1) / denominator // 第二个自回归系数
Lợi thế của phương pháp này là nó không dựa vào sự phán đoán chủ quan, mà để cho dữ liệu tự “nói” và khám phá ra các định kỳ ẩn trong chuỗi giá.
Tại sao mô hình GARCH có thể mô tả rủi ro thị trường tốt hơn?
Chỉ có mô hình AR là không đủ, vì sự biến động của thị trường tài chính không phải là cố định. Chúng ta đều biết rằng sự biến động lớn thường đi kèm với biến động lớn, và thời gian yên tĩnh thường kéo dài hơn.
Mô hình GARCH ((1,1) được thiết kế để mô tả đặc điểm này:
σ²_t = ω + α × ε²_{t-1} + β × σ²_{t-1}
Lập trình trong mã đã thể hiện rõ điều này:
omega = (1 - adjustedAlpha - adjustedBeta) * longTermVar
garchVariance := omega + adjustedAlpha * math.pow(arResidual[1], 2) + adjustedBeta * garchVariance[1]
Những hiểu biết quan trọng ở đây là: tỷ lệ chênh lệch điều kiện hiện tại phụ thuộc không chỉ vào chênh lệch dư thừa bình phương của giai đoạn trước ((động thái ngắn hạn), mà còn phụ thuộc vào tỷ lệ chênh lệch điều kiện của giai đoạn trước ((sự liên tục dài hạn)). Các tham số α kiểm soát ảnh hưởng của các tác động ngắn hạn, β kiểm soát sự liên tục của tỷ lệ biến động.
Lập luận giao dịch của chiến lược này có thể cân bằng giữa rủi ro và lợi nhuận như thế nào?
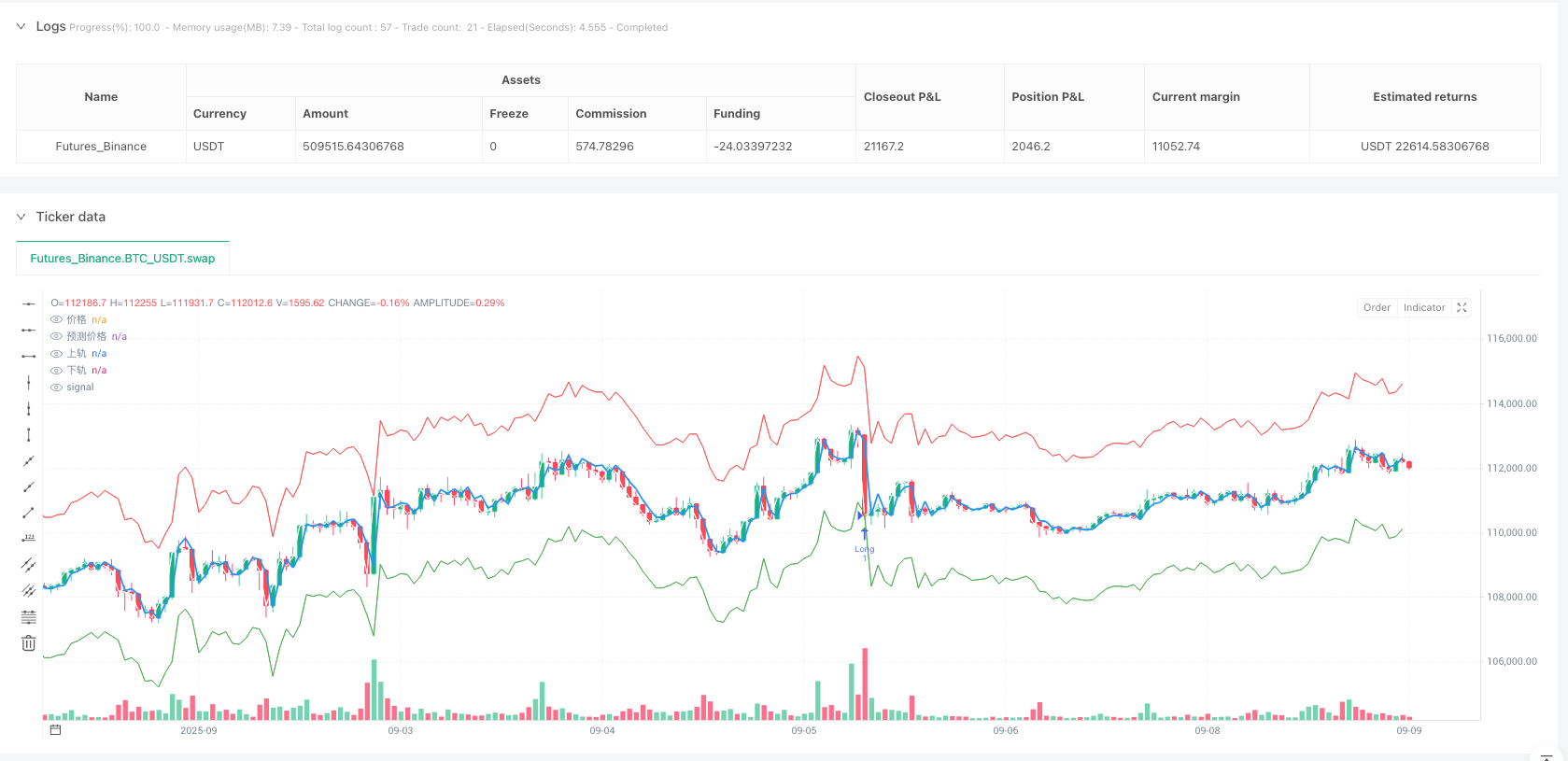
Với dự đoán AR và ước tính biến động GARCH, chiến lược xây dựng khoảng tin cậy động:
upperReturnBand = arReturnPredict + stdevFactor * garchStd
lowerReturnBand = arReturnPredict - stdevFactor * garchStd
Logic tạo ra tín hiệu giao dịch thể hiện ý tưởng về hồi quy trung bình:
- LongSignal = rawPrice < lowerPriceBand)
- Khi giá phá vỡ đường ray trên
Sự tinh tế của thiết kế này là: chiều rộng của khoảng tin cậy sẽ được điều chỉnh theo động thái biến động của thị trường. Trong thời gian biến động cao, khoảng rộng hơn, giảm tần suất giao dịch; trong thời gian biến động thấp, khoảng hẹp hơn, tăng cơ hội giao dịch.
Những vấn đề quan trọng nào cần chú ý trong ứng dụng thực tế?
1. Kiểm tra độ ổn định mô hình Mã này bao gồm các kiểm tra ổn định quan trọng:
if stabilityCheck >= 0.99 or math.abs(phi2) >= 0.99
scaleFactor = 0.95 / math.max(stabilityCheck, math.abs(phi2) + 0.01)
Điều này đảm bảo sự ổn định của mô hình AR và tránh các kết quả dự đoán phân tán.
2. Rõ ràng ràng buộc đối với tham số hội tụ Mô hình GARCH yêu cầu α + β < 1 để đảm bảo sự khác biệt dài hạn:
if sumParam >= 0.999
scale = 0.99 / sumParam
3. Nhu cầu về cơ chế lọc Chiến lược cung cấp các tùy chọn lọc RSI, điều này rất quan trọng trong ứng dụng thực tế. Mô hình thống kê thuần túy có thể bỏ qua các đặc điểm xu hướng của thị trường, và việc thêm các chỉ số kỹ thuật có thể cung cấp tín hiệu xác nhận bổ sung.
Hạn chế và phương hướng cải thiện chiến lược
Mặc dù chiến lược này có vẻ thanh lịch về mặt lý thuyết, nhưng trong thực tế, nó vẫn cần phải được xem xét:
Chọn tần số dữ liệu: Mô hình AR-GARCH có sự khác biệt lớn trong hiệu suất trong các chu kỳ khác nhau. Dữ liệu tần số cao có thể cung cấp nhiều thông tin hơn, nhưng cũng giới thiệu nhiều tiếng ồn hơn.
Tính biến đổi theo thời gian của tham số: Thực hiện hiện giả định AR và GARCH tham số là không đổi trong cửa sổ ước tính, nhưng cấu trúc thị trường thực tế có thể thay đổi.
Tác động của chi phí giao dịchCác chiến lược mạo hiểm thống kê thường đòi hỏi tần suất giao dịch cao hơn, phí và chi phí trượt không thể bỏ qua.
Kết luận: Giá trị của mô hình thống kê trong giao dịch định lượng
Chiến lược AR-GARCH cho thấy sức mạnh của thống kê hiện đại trong mô hình tài chính. Nó không chỉ đơn giản là một bộ chỉ số kỹ thuật, mà là sự khai thác sâu sắc về tính chất thống kê của chuỗi thời gian tài chính.
Đối với các nhà giao dịch định lượng, giá trị của việc hiểu được các chiến lược này không chỉ nằm ở việc áp dụng trực tiếp mà còn ở khả năng phân tích thị trường bằng tư duy thống kê. Ngày nay, khi AI và học máy đang phổ biến, các mô hình thống kê cổ điển này vẫn là nền tảng quan trọng để chúng ta hiểu thị trường và xây dựng chiến lược.
/*backtest
start: 2025-04-01 00:00:00
end: 2025-09-09 08:00:00
period: 1h
basePeriod: 1h
exchanges: [{"eid":"Futures_Binance","currency":"BTC_USDT","balance":500000}]
*/
//@version=5
strategy("AR(2)-GARCH Strategy", overlay=true)
//策略参数设置:配置AR模型、GARCH模型和交易信号的各项参数
lengthReg = input.int(50, "AR估计窗口", minval=50, maxval=200);//AR模型回归窗口长度
//GARCH波动率模型参数:控制条件方差的计算
useGarch = input.bool(true, "启用GARCH波动率");//是否启用GARCH波动率建模
garchAlpha = input.float(0.1, "GARCH Alpha", minval=0.01, maxval=0.3, step=0.01);//GARCH模型alpha参数
garchBeta = input.float(0.85, "GARCH Beta", minval=0.5, maxval=0.95, step=0.01);//GARCH模型beta参数
//交易信号生成参数:控制买卖信号的敏感度
stdevFactor = input.float(2.0, "标准差倍数", minval=1.0, maxval=3.0, step=0.1);//交易波段的标准差倍数
//风险控制参数:设置止损止盈水平
stopLossPerc = input.float(2.0, "止损 (%)", minval=0.5, maxval=5.0, step=0.1);//止损百分比
takeProfitPerc = input.float(4.0, "止盈 (%)", minval=1.0, maxval=10.0, step=0.1);//止盈百分比
//RSI过滤器参数:添加技术指标过滤条件
useRsiFilter = input.bool(false, "启用RSI过滤");//是否启用RSI过滤器
rsiLen = input.int(14, "RSI周期", minval=7, maxval=21);//RSI指标计算周期
rsiOB = input.float(70, "RSI超买线", minval=60, maxval=80);//RSI超买阈值
rsiOS = input.float(30, "RSI超卖线", minval=20, maxval=40);//RSI超卖阈值
//数据预处理:计算收益率序列
rawPrice = close;//原始收盘价
returns = math.log(rawPrice / rawPrice[1]);//对数收益率序列
//获取滞后收益率数据:AR(2)模型需要前两期的收益率数据
returns1 = returns[1];//滞后1期的收益率
returns2 = returns[2];//滞后2期的收益率
//计算收益率序列的移动平均值:作为AR模型的均值项
returnsMean = ta.sma(returns, lengthReg);//收益率的简单移动平均
//AR(2)模型系数计算:使用Yule-Walker方程求解自回归系数
//自协方差函数计算:计算不同滞后期的自协方差
calcAutoCovariance(data, lag, length) =>
mean = ta.sma(data, length);//计算数据的均值
sum = 0.0;//协方差累计值
count = 0;//有效数据点计数
for i = lag to length - 1
if not na(data[i]) and not na(data[i-lag])
sum := sum + (data[i] - mean) * (data[i-lag] - mean);//计算协方差分子
count := count + 1;//累计有效数据点
count > 0 ? sum / count : 0.0;//返回协方差值
//计算AR(2)模型所需的自协方差:用于Yule-Walker方程
c0 = calcAutoCovariance(returns, 0, lengthReg);//滞后0期的自协方差(即方差)
c1 = calcAutoCovariance(returns, 1, lengthReg);//滞后1期的自协方差
c2 = calcAutoCovariance(returns, 2, lengthReg);//滞后2期的自协方差
//Yule-Walker方程求解:计算AR(2)模型的两个自回归系数
// φ₁ = (c₁c₀ - c₂c₁) / (c₀² - c₁²)
// φ₂ = (c₂c₀ - c₁²) / (c₀² - c₁²)
denominator = c0 * c0 - c1 * c1;//分母计算
phi1 = denominator != 0 ? (c1 * c0 - c2 * c1) / denominator : 0.0;//第一个自回归系数
phi2 = denominator != 0 ? (c2 * c0 - c1 * c1) / denominator : 0.0;//第二个自回归系数
//AR(2)稳定性检验:确保模型稳定性条件 |φ₁| + |φ₂| < 1 且 |φ₂| < 1
stabilityCheck = math.abs(phi1) + math.abs(phi2);//计算系数绝对值之和
if stabilityCheck >= 0.99 or math.abs(phi2) >= 0.99
scaleFactor = 0.95 / math.max(stabilityCheck, math.abs(phi2) + 0.01);//计算缩放因子
phi1 := phi1 * scaleFactor;//调整第一个系数
phi2 := phi2 * scaleFactor;//调整第二个系数
//AR(2)收益率预测:根据历史收益率和AR系数预测下一期收益率
arReturnPredict = returnsMean + phi1 * (returns1 - returnsMean) + phi2 * (returns2 - returnsMean);//AR(2)预测公式
//计算AR模型的预测残差:用于GARCH建模
arResidual = returns - arReturnPredict;//AR模型的预测残差
//GARCH(1,1)波动率建模:对AR残差进行条件方差建模
var float garchVariance = na;//GARCH方差变量
var float longTermVar = na;//长期方差变量
//长期方差初始化:使用历史残差计算初始方差值
if na(longTermVar) and bar_index > lengthReg
longTermVar := ta.variance(arResidual, lengthReg);//计算长期方差
//GARCH参数调整:确保参数满足收敛条件
adjustedAlpha = garchAlpha;//调整后的alpha参数
adjustedBeta = garchBeta;//调整后的beta参数
sumParam = garchAlpha + garchBeta;//参数和
if sumParam >= 0.999
scale = 0.99 / sumParam;//计算参数缩放比例
adjustedAlpha := garchAlpha * scale;//调整alpha参数
adjustedBeta := garchBeta * scale;//调整beta参数
//GARCH(1,1)递归更新:根据GARCH公式更新条件方差
if useGarch and not na(longTermVar) and not na(arResidual)
if na(garchVariance)
garchVariance := longTermVar;//初始化GARCH方差
else
omega = (1 - adjustedAlpha - adjustedBeta) * longTermVar;//GARCH常数项
garchVariance := omega + adjustedAlpha * math.pow(arResidual[1], 2) + adjustedBeta * garchVariance[1];//GARCH递归公式
//条件标准差计算:从条件方差计算标准差
garchStd = useGarch and not na(garchVariance) ? math.sqrt(math.max(garchVariance, 0.0001)) : ta.stdev(arResidual, 20);//启用GARCH时使用条件标准差,否则使用历史标准差
//收益率空间的置信区间构建:基于AR预测和GARCH波动率
upperReturnBand = arReturnPredict + stdevFactor * garchStd;//上轨:预测收益率加上标准差倍数
lowerReturnBand = arReturnPredict - stdevFactor * garchStd;//下轨:预测收益率减去标准差倍数
//将置信区间转换为价格空间:用于实际交易信号生成
//基于预测收益率计算预测价格
predictedPrice = rawPrice[1] * math.exp(arReturnPredict);//根据预测收益率计算预测价格
upperPriceBand = rawPrice[1] * math.exp(upperReturnBand);//上轨价格
lowerPriceBand = rawPrice[1] * math.exp(lowerReturnBand);//下轨价格
//交易信号生成:基于当前价格相对于置信区间的位置
longSignal = rawPrice < lowerPriceBand;//做多信号:当前价格低于下轨
shortSignal = rawPrice > upperPriceBand;//做空信号:当前价格高于上轨
//RSI过滤器:使用RSI指标过滤交易信号
if useRsiFilter
rsi = ta.rsi(rawPrice, rsiLen);//计算RSI指标
longSignal := longSignal and rsi < rsiOS;//做多信号需要RSI超卖确认
shortSignal := shortSignal and rsi > rsiOB;//做空信号需要RSI超买确认
//策略执行:根据交易信号开仓和平仓
//开仓操作:根据信号建立多头或空头仓位
if longSignal
strategy.entry("Long", strategy.long);//开多仓
if shortSignal
strategy.entry("Short", strategy.short);//开空仓
//风险控制:设置止损止盈条件
if strategy.position_size > 0
strategy.exit("Long Exit", "Long",
stop=strategy.position_avg_price * (1 - stopLossPerc/100),
limit=strategy.position_avg_price * (1 + takeProfitPerc/100));//多仓止损止盈
if strategy.position_size < 0
strategy.exit("Short Exit", "Short",
stop=strategy.position_avg_price * (1 + stopLossPerc/100),
limit=strategy.position_avg_price * (1 - takeProfitPerc/100));//空仓止损止盈
//图表显示:在图表上绘制价格、预测线和交易信号
//主要价格线和预测线:显示实际价格和基于收益率预测的价格
plot(rawPrice, color=color.white, linewidth=1, title="价格");//绘制实际价格线
plot(predictedPrice, color=color.blue, linewidth=2, title="预测价格");//绘制预测价格线
plot(upperPriceBand, color=color.red, linewidth=1, title="上轨");//绘制上轨线
plot(lowerPriceBand, color=color.green, linewidth=1, title="下轨");//绘制下轨线
//交易信号标记:在图表上标记买卖信号点
plotshape(longSignal, style=shape.triangleup, location=location.belowbar,
color=color.green, size=size.small, title="买入");//标记买入信号
plotshape(shortSignal, style=shape.triangledown, location=location.abovebar,
color=color.red, size=size.small, title="卖出");//标记卖出信号