দয়া করে নোট করুনঃ এই কেসটি শুধুমাত্র গবেষণা ও শিক্ষার জন্য তৈরি করা হয়েছে এবং এটি বিনিয়োগের পরামর্শ নয়।

বিটকয়েনের দামের তথ্য সময়ক্রম ভিত্তিক, তাই বিটকয়েনের দামের পূর্বাভাস বেশিরভাগই এলএসটিএম মডেল ব্যবহার করে করা হয়।

দীর্ঘস্থায়ী স্বল্পমেয়াদী স্মৃতি (LSTM) একটি গভীর শিক্ষণ মডেল যা বিশেষত টাইম সিকোয়েন্স ডেটা (অথবা এমন ডেটা যা সময় / স্থানিক / কাঠামোগত ক্রমযুক্ত, যেমন চলচ্চিত্র, বাক্য ইত্যাদি) এর জন্য উপযুক্ত। এটি ক্রিপ্টোকারেন্সির দামের দিকনির্দেশের জন্য আদর্শ মডেল।

এই নিবন্ধটি মূলত বিটকয়েনের ভবিষ্যতের দামের পূর্বাভাস দেওয়ার জন্য এলএসটিএম-এর মাধ্যমে ডেটা সমন্বয় করা হয়েছে।

আমদানির জন্য প্রয়োজনীয় লাইব্রেরি

import pandas as pd
import numpy as np

from sklearn.preprocessing import MinMaxScaler, LabelEncoder
from keras.models import Sequential
from keras.layers import LSTM, Dense, Dropout

from matplotlib import pyplot as plt
%matplotlib inline

তথ্য বিশ্লেষণ

তথ্য লোড হচ্ছে

বিটিসির দৈনিক লেনদেনের তথ্য পড়ুন

data = pd.read_csv(filepath_or_buffer="btc_data_day")

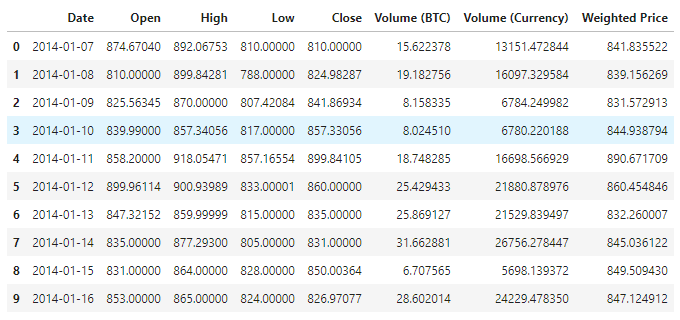
ডেটা দেখতে পাওয়া যায়, বর্তমানে ১৩৮০ টি ডাটা রয়েছে, ডেটা তারিখ, ওপেন, হাই, লো, ক্লোজ, ভলিউম (বিটিসি), ভলিউম (মুদ্রা) এবং ওজনযুক্ত মূল্যের কলামগুলি নিয়ে গঠিত। তারিখ কলাম বাদে, অন্যান্য সমস্ত ডাটা কলাম ফ্লোট৬৪ ডেটা টাইপ।

data.info()

প্রথম দশটি লাইন দেখুন।

data.head(10)

ডেটা ভিজ্যুয়ালাইজেশন

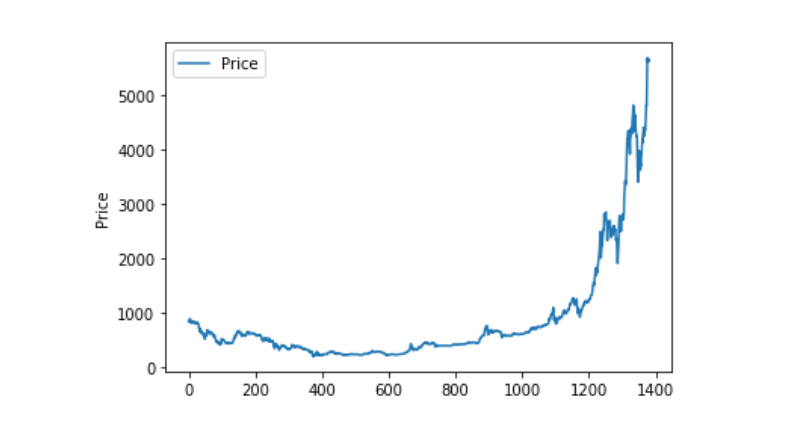
matplotlib ব্যবহার করে Weighted Price ম্যাপ করুন, এবং দেখুন কিভাবে ডেটা বন্টন এবং ট্র্যাফিক চলছে। আমরা একটি অংশে ডেটা 0 পেয়েছি, এবং আমরা নিশ্চিত করতে চাই যে ডেটা অস্বাভাবিক কিনা।

plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()

অস্বাভাবিক তথ্য প্রক্রিয়াকরণ

এখন আমরা দেখতে পারি যে, আমাদের ডেটাতে ন্যান ডেটা আছে কি না।

data.isnull().sum()

Date                 0
Open                 0
High                 0
Low                  0
Close                0
Volume (BTC)         0
Volume (Currency)    0
Weighted Price       0
dtype: int64

এখন আমরা 0 এর দিকে তাকাই, এবং আমরা দেখতে পাচ্ছি যে আমাদের ডেটাতে 0 এর মান রয়েছে, এবং আমরা 0 এর মান নিয়ে কাজ করতে চাই।

(data == 0).astype(int).any()

Date                 False
Open                  True
High                  True
Low                   True
Close                 True
Volume (BTC)          True
Volume (Currency)     True
Weighted Price        True
dtype: bool

data['Weighted Price'].replace(0, np.nan, inplace=True)
data['Weighted Price'].fillna(method='ffill', inplace=True)
data['Open'].replace(0, np.nan, inplace=True)
data['Open'].fillna(method='ffill', inplace=True)
data['High'].replace(0, np.nan, inplace=True)
data['High'].fillna(method='ffill', inplace=True)
data['Low'].replace(0, np.nan, inplace=True)
data['Low'].fillna(method='ffill', inplace=True)
data['Close'].replace(0, np.nan, inplace=True)
data['Close'].fillna(method='ffill', inplace=True)
data['Volume (BTC)'].replace(0, np.nan, inplace=True)
data['Volume (BTC)'].fillna(method='ffill', inplace=True)
data['Volume (Currency)'].replace(0, np.nan, inplace=True)
data['Volume (Currency)'].fillna(method='ffill', inplace=True)

(data == 0).astype(int).any()

Date                 False
Open                 False
High                 False
Low                  False
Close                False
Volume (BTC)         False
Volume (Currency)    False
Weighted Price       False
dtype: bool

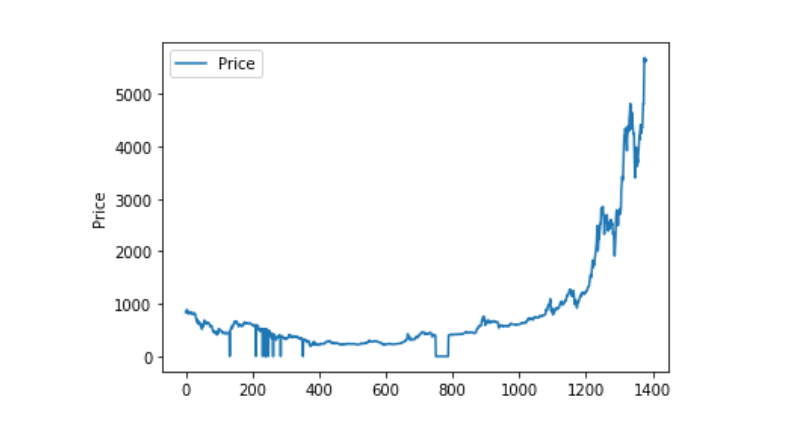
এখন, যদি আমরা তথ্যের বন্টন এবং গতির দিকে তাকাই, তাহলে আমরা দেখতে পাব যে, এই সময়টাতে কার্ভটি বেশ ধারাবাহিক ছিল।

plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()

প্রশিক্ষণ ডেটাসেট এবং পরীক্ষার ডেটাসেট বিভক্ত করা

0 থেকে 1 পর্যন্ত তথ্য একত্রিত করুন

data_set = data.drop('Date', axis=1).values
data_set = data_set.astype('float32')
mms = MinMaxScaler(feature_range=(0, 1))
data_set = mms.fit_transform(data_set)

টেস্ট ডেটাসেট এবং প্রশিক্ষণ ডেটাসেটকে ২ঃ৮ ভাগ করে নিন

ratio = 0.8
train_size = int(len(data_set) * ratio)
test_size = len(data_set) - train_size
train, test = data_set[0:train_size,:], data_set[train_size:len(data_set),:]

আমাদের প্রশিক্ষণ ডেটাসেট এবং টেস্টিং ডেটাসেট তৈরি করতে একটি উইন্ডো পিরিয়ড হিসাবে 1 দিন ব্যবহার করুন।

def create_dataset(data):
    window = 1
    label_index = 6
    x, y = [], []
    for i in range(len(data) - window):
        x.append(data[i:(i + window), :])
        y.append(data[i + window, label_index])
    return np.array(x), np.array(y)

train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)

মডেল সংজ্ঞায়িত এবং প্রশিক্ষণ

এইবার আমরা একটি সহজ মডেল ব্যবহার করব, যে মডেলের গঠন হল 1. LSTM2. Dense。

এখানে LSTM-এর inputh shape-এর ব্যাপারে কিছু বলা দরকার, Input Shape-এর ইনপুট মাত্রা হল ((batch_size, time steps, features) । এর মধ্যে, time steps মান হল ডেটা ইনপুট করার সময় সময় উইন্ডোর অন্তর, এখানে আমরা 1 দিনকে সময় উইন্ডো হিসেবে ব্যবহার করি, এবং আমাদের ডেটা হল দৈনিক ডেটা, তাই এখানে আমাদের time steps হল 1 ।

লং শর্ট-টার্ম মেমোরি (LSTM) হল একটি বিশেষ ধরনের RNN, যা মূলত লং সিকোয়েন্স প্রশিক্ষণের সময় গ্রেডিয়েন্ট হারিয়ে যাওয়া এবং গ্রেডিয়েন্ট বিস্ফোরণের সমস্যার সমাধানের জন্য ব্যবহৃত হয়।

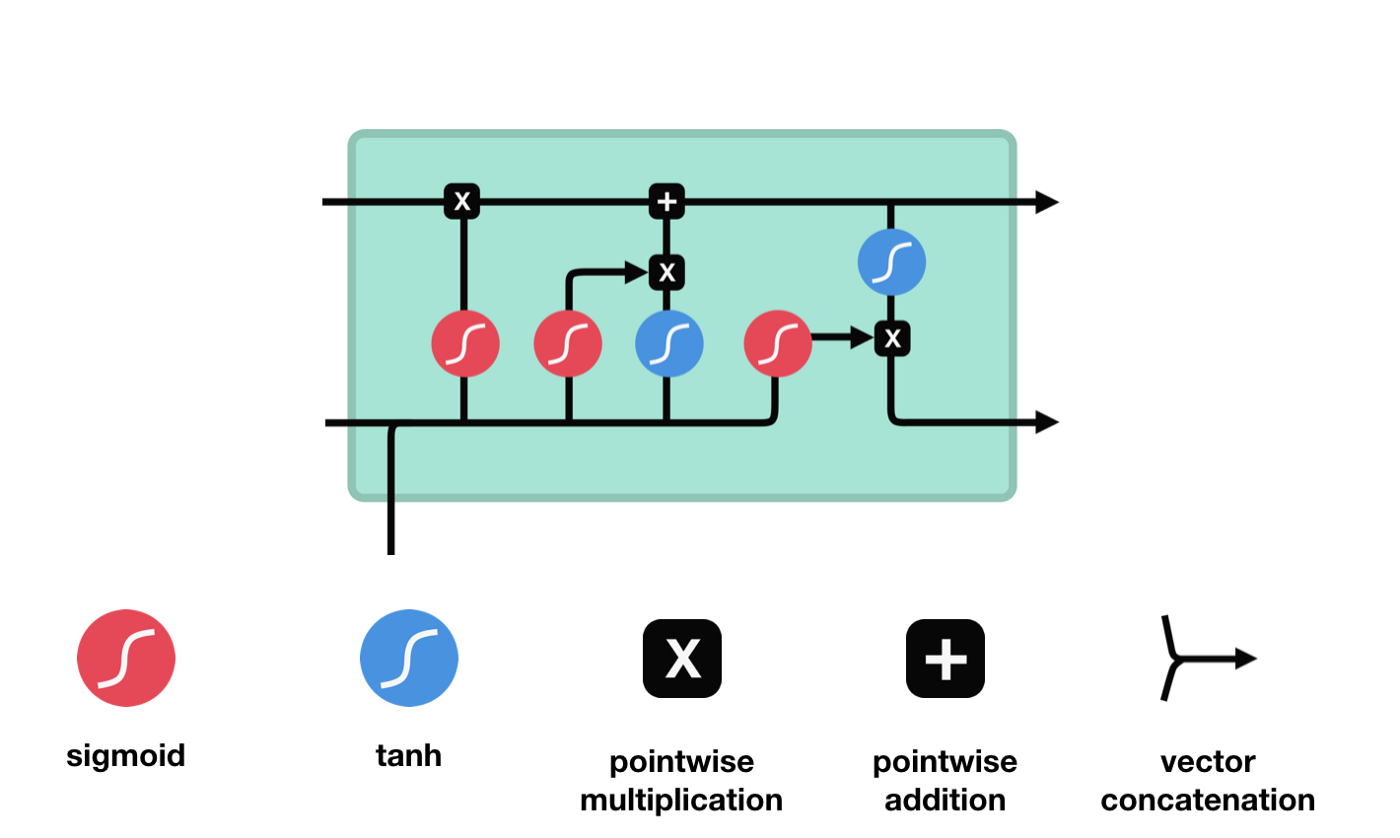
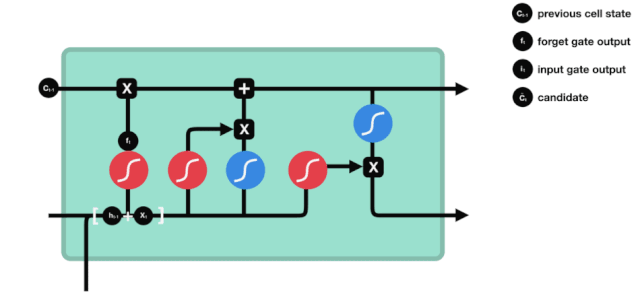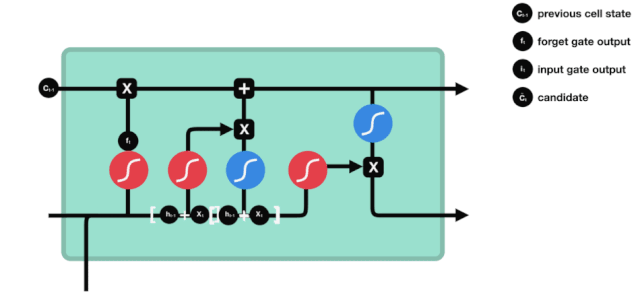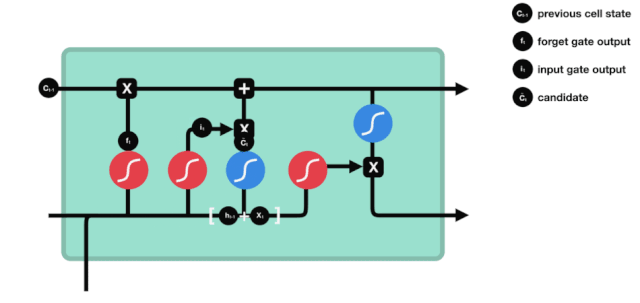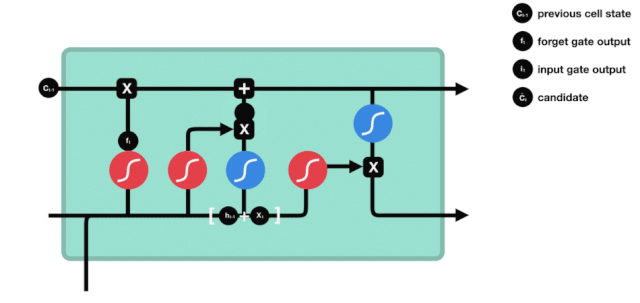
এলএসটিএমের নেটওয়ার্ক স্ট্রাকচার ডায়াগ্রাম থেকে দেখা যায় যে এলএসটিএম আসলে একটি ছোট মডেল, যার মধ্যে রয়েছে 3 টি সিগময়েড অ্যাক্টিভেশন ফাংশন, 2 টি তানহ অ্যাক্টিভেশন ফাংশন, 3 টি গুণক এবং 1 টি যোগ।

কোষের অবস্থা

সেল স্টেট হল এলএসটিএম এর মূল অংশ, এটি হল উপরের চিত্রের উপরের কালো রেখা, এবং এই কালো রেখার নিচে কিছু দরজা রয়েছে, যা আমরা পরে আলোচনা করব। সেল স্টেট আপডেট করা হবে প্রতিটি দরজার ফলাফলের উপর নির্ভর করে। নীচে আমরা এই দরজা সম্পর্কে আলোচনা করব এবং আপনি সেল স্টেট প্রক্রিয়াটি বুঝতে পারবেন।

LSTM নেটওয়ার্কগুলি একটি গেট নামে পরিচিত একটি কাঠামোর মাধ্যমে কোষের অবস্থা থেকে তথ্য মুছে ফেলতে বা যুক্ত করতে পারে। গেটগুলি নির্বাচনী সিদ্ধান্ত নিতে পারে যে কোন তথ্যটি পাস করতে হবে। গেট কাঠামোটি একটি সিগময়েড স্তর এবং একটি বিন্দু গুণিতক অপারেশনগুলির সমন্বয়। যেহেতু সিগময়েড স্তরের আউটপুটটি 0-1 এর মান, 0 এর কোনওটিই পাস করা যায় না, 1 এর কোনওটিই পাস করা যায় না। একটি LSTM এর মধ্যে তিনটি গেট রয়েছে যা কোষের অবস্থা নিয়ন্ত্রণ করে। নীচে আমরা সেগুলি একের পর এক আলোচনা করব।

ভুলে যাওয়ার দরজা

LSTM এর প্রথম ধাপ হল কোষের অবস্থা থেকে কোন তথ্যকে বাদ দিতে হবে তা নির্ধারণ করা। এই অংশটি একটি সিগময়েড ইউনিট দ্বারা পরিচালিত হয় যাকে ভুলে যাওয়ার দরজা বলা হয়।

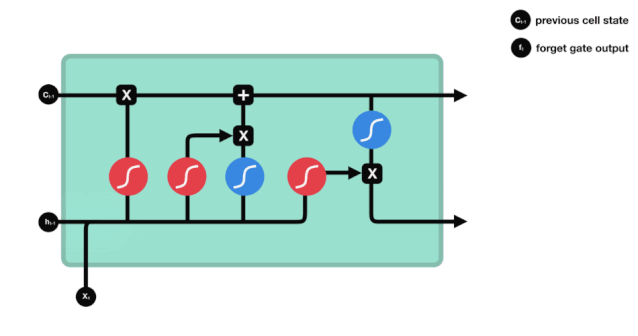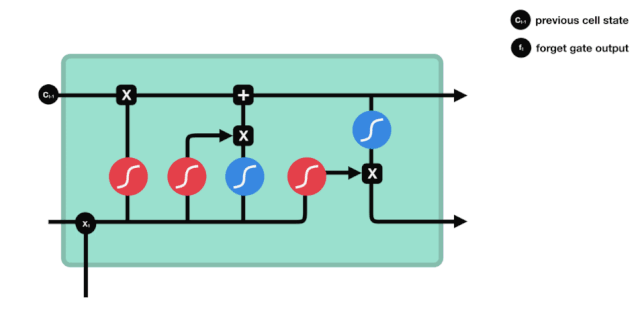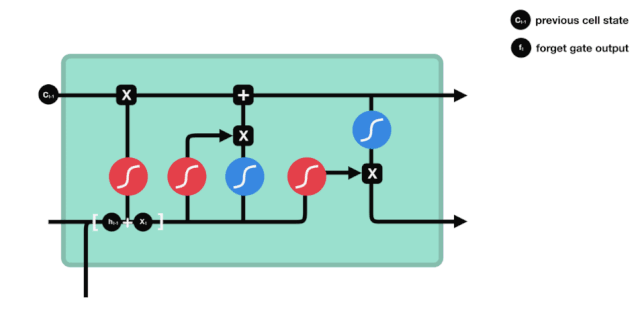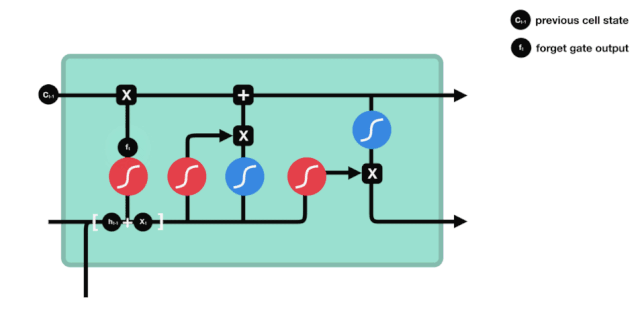
আমরা দেখতে পাচ্ছি যে ভুলে যাওয়া গেটটি \(h_{l-1}\) এবং \(x_{t}\) তথ্যের মাধ্যমে একটি ভেক্টর 0-1 এর মধ্যে একটি ভেক্টর আউটপুট করে। ভেক্টরের মধ্যে 0-1 মানটি নির্দেশ করে যে কোষের অবস্থা \(C_{t-1}\) এর মধ্যে কোন তথ্য সংরক্ষণ করা হয়েছে বা কতটুকু বাদ দেওয়া হয়েছে। 0 মানে সংরক্ষণ করা হয়নি এবং 1 মানে সংরক্ষণ করা হয়েছে।

\(f_{t}= এর গাণিতিক প্রকাশ\sigma\left(W_{f} \cdot\left[h_{t-1}, x_{t}\right]+b_{f}\right)\)

প্রবেশদ্বার

পরবর্তী ধাপ হল কোষের অবস্থা সম্পর্কে নতুন তথ্য যোগ করার সিদ্ধান্ত নেওয়া, যা ইনপুট দিয়ে সম্পন্ন করা হয়। প্রথমে আমরা অ্যানিমেটেড ডায়াগ্রামটি দেখি, যেখানে কোষের অবস্থা সম্পর্কে নতুন তথ্য যোগ করা হয়।

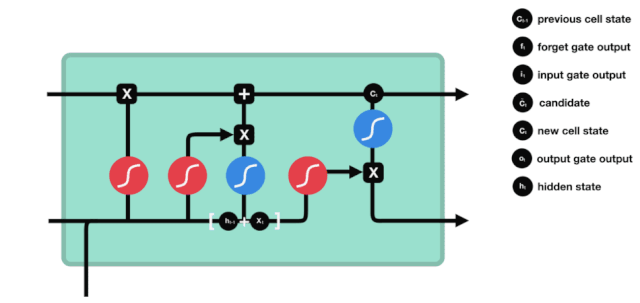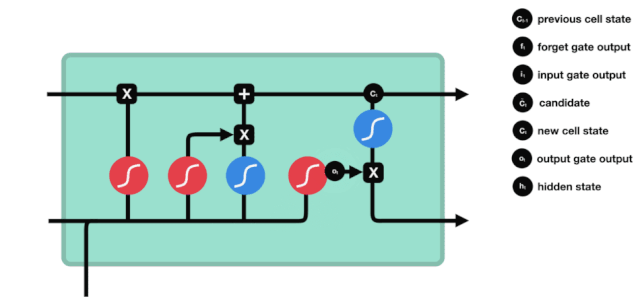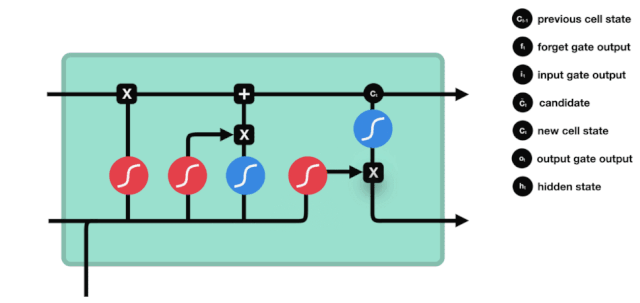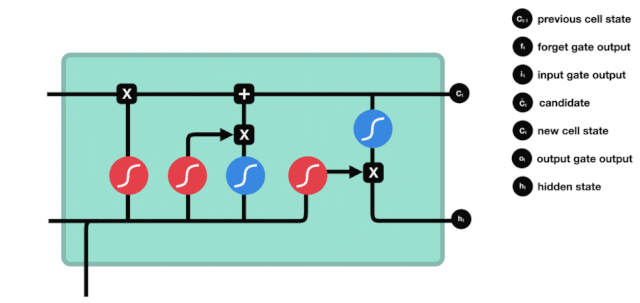
আমরা দেখলাম যে \(h_{l-1}\) এবং \(x_{t}\) এর তথ্য একটি ভুলে যাওয়া গেট (sigmoid) এবং ইনপুট গেট (tanh) এর মধ্যে রাখা হয়েছে। যেহেতু ভুলে যাওয়া গেটের আউটপুটটি 0-1 এর মান, তাই যদি ভুলে যাওয়া গেটটি 0 হয় তবে ইনপুট গেটের পরবর্তী ফলাফল \(C_{i}\) বর্তমান কোষের অবস্থানে যোগ করা হবে না, যদি এটি 1 হয় তবে এটি সমস্ত কোষের অবস্থানে যোগ করা হবে, তাই এখানে ভুলে যাওয়া গেটটি ইনপুট গেটটির ফলাফলকে নির্বাচন করে কোষের অবস্থানে যোগ করা হবে।

\(C_{t}=f_{t} * C_{t-1}+i_{t} * এর গাণিতিক সূত্র\tilde{C}_{t}\)

প্রস্থান দরজা

কোষের অবস্থা আপডেট করার পরে, \(h_{l-1}\) এবং \(x_{t}\) ইনপুটের সমষ্টি অনুসারে আউটপুট কোষের কোন অবস্থা বৈশিষ্ট্যগুলি বিচার করা প্রয়োজন, এখানে আউটপুটটি আউটপুট গেট নামে পরিচিত একটি সিগময়েড স্তর দিয়ে বিচার করা প্রয়োজন, তারপরে কোষের অবস্থাটি টানহ স্তর দিয়ে একটি ভেক্টর পাবেন যা -1 ~ 1 এর মধ্যে মান পাবে, এই ভেক্টরটি আউটপুট গেট দ্বারা বিচার করা হয় যা চূড়ান্ত RNN ইউনিটটির আউটপুট পায়। অ্যানিমেশনটির উদ্দেশ্য নিম্নরূপঃ

def create_model():
    model = Sequential()
    model.add(LSTM(50, input_shape=(train_x.shape[1], train_x.shape[2])))
    model.add(Dense(1))
    model.compile(loss='mae', optimizer='adam')
    model.summary()
    return model

model = create_model()

history = model.fit(train_x, train_y, epochs=80, batch_size=64, validation_data=(test_x, test_y), verbose=1, shuffle=False)

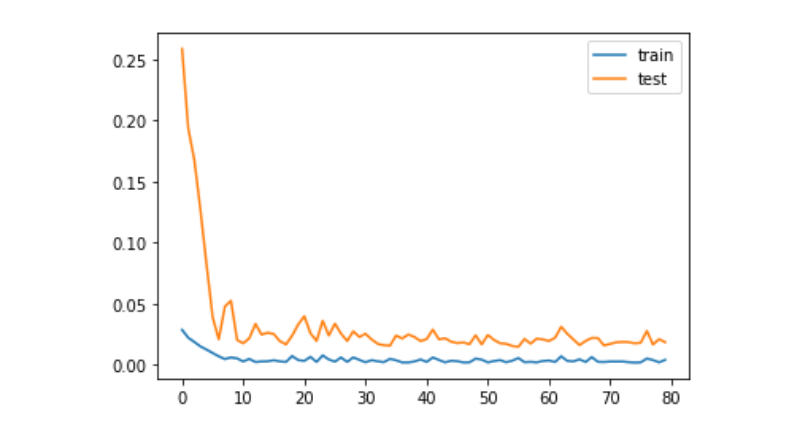
plt.plot(history.history['loss'], label='train')
plt.plot(history.history['val_loss'], label='test')
plt.legend()
plt.show()

train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)

পূর্বাভাস

predict = model.predict(test_x)
plt.plot(predict, label='predict')
plt.plot(test_y, label='ground true')
plt.legend()
plt.show()

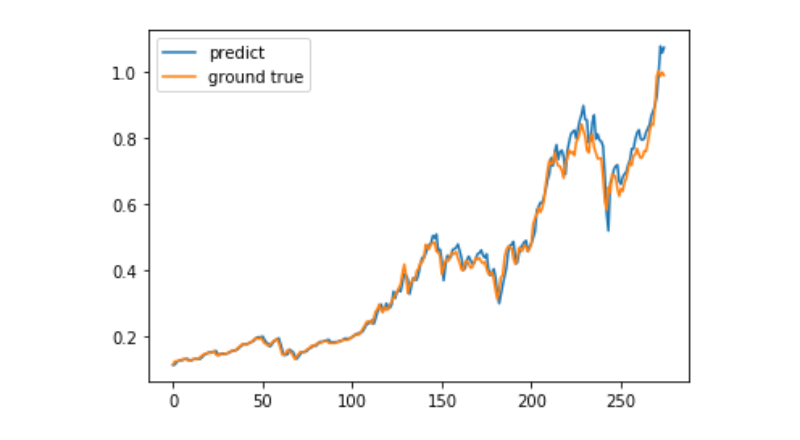
মেশিন লার্নিং ব্যবহার করে বিটকয়েনের দীর্ঘমেয়াদী মূল্যের গতিবিধি ভবিষ্যদ্বাণী করা এখনও খুব কঠিন, এই নিবন্ধটি কেবলমাত্র একটি শিক্ষণ কেস হিসাবে ব্যবহার করা যেতে পারে। এই কেসটি পরে ম্যাকপুলের মেঘের সাথে ডেমো ইমেজগুলিতে অনলাইনে আসবে, আগ্রহী ব্যবহারকারীরা সরাসরি অভিজ্ঞতা অর্জন করতে পারবেন।