পূর্ববর্তী একটি নিবন্ধে, আমরা ডিজিটাল মুদ্রার বাজারে একটি সাধারণ ঘটনা নিয়ে আলোচনা করেছি: বেশিরভাগ ডিজিটাল মুদ্রা, বিশেষ করে যেগুলি বিটকয়েন এবং ইথেরিয়ামের দামের ওঠানামা অনুসরণ করে, প্রায়ই একই সময়ে বৃদ্ধি এবং পতনের প্রবণতা দেখায়। এই ঘটনাটি মূলধারার মুদ্রার সাথে তাদের উচ্চ পারস্পরিক সম্পর্ক প্রকাশ করে। যাইহোক, বিভিন্ন ডিজিটাল মুদ্রার মধ্যে পারস্পরিক সম্পর্কের মাত্রাও পরিবর্তিত হয়। তাহলে, পারস্পরিক সম্পর্কের এই পার্থক্য কীভাবে প্রতিটি মুদ্রার বাজারের কর্মক্ষমতাকে প্রভাবিত করে? এই নিবন্ধে, আমরা উদাহরণ হিসাবে 2023 সালের দ্বিতীয়ার্ধে ষাঁড়ের বাজার ব্যবহার করে এই সমস্যাটি অন্বেষণ করব।

ডিজিটাল কারেন্সি মার্কেটের সিঙ্ক্রোনিক রুট

ডিজিটাল মুদ্রা বাজার তার অস্থিরতা এবং অনিশ্চয়তার জন্য পরিচিত। বিটকয়েন এবং ইথেরিয়াম, বাজারের দুটি দৈত্য হিসাবে, প্রায়শই দামের গতিবিধিতে অগ্রণী ভূমিকা পালন করে। বেশিরভাগ ছোট বা উদীয়মান ডিজিটাল মুদ্রা, বাজারের প্রতিযোগিতা এবং সক্রিয় ট্রেডিং বজায় রাখার জন্য, এই মূলধারার মুদ্রাগুলির সাথে, বিশেষ করে প্রকল্পের পক্ষের বাজার-নির্মাণ মুদ্রাগুলির সাথে একটি নির্দিষ্ট মাত্রার মূল্য সমন্বয় বজায় রাখার প্রবণতা রাখে। এই সিঙ্ক্রোনিসিটি বাজারের অংশগ্রহণকারীদের মনস্তাত্ত্বিক প্রত্যাশা এবং ট্রেডিং কৌশলগুলিকে প্রতিফলিত করে এবং পরিমাণগত ট্রেডিং কৌশলগুলির নকশায় এটি একটি গুরুত্বপূর্ণ বিবেচ্য।

পারস্পরিক সম্পর্ক সূত্র এবং গণনার পদ্ধতি

পরিমাণগত ব্যবসায়ের ক্ষেত্রে, পারস্পরিক সম্পর্ক পরিসংখ্যানগত পদ্ধতির মাধ্যমে পরিমাপ করা হয়। সর্বাধিক ব্যবহৃত পরিমাপ হল পিয়ারসন পারস্পরিক সম্পর্ক সহগ, যা দুটি ভেরিয়েবলের মধ্যে রৈখিক পারস্পরিক সম্পর্কের মাত্রা পরিমাপ করে। এখানে কিছু মূল ধারণা এবং গণনা পদ্ধতি রয়েছে:

পিয়ারসন পারস্পরিক সম্পর্ক সহগ (উল্লেখিত \(r\)) -1 থেকে +1 পর্যন্ত পরিসীমা, যেখানে +1 একটি নিখুঁত ইতিবাচক সম্পর্ক নির্দেশ করে, -1 একটি নিখুঁত নেতিবাচক সম্পর্ক নির্দেশ করে, এবং 0 কোন রৈখিক সম্পর্ক নির্দেশ করে না। সহগ নিম্নরূপ গণনা করা হয়:

\(r = \frac{\sum_{i=1}^{n} (X_i - \bar{X})(Y_i - \bar{Y})}{\sqrt{\sum_{i=1}^{n} (X_i - \bar{X})^2} \sqrt{\sum_{i=1}^{n} (Y_i - \bar{Y})^2}}\)

তাদের মধ্যে, \(X_i\) এবং \(Y_i\) হল দুটি র্যান্ডম ভেরিয়েবলের পর্যবেক্ষিত মান এবং \(\bar{X}\) এবং \(\bar{Y}\) হল যথাক্রমে এই দুটি র্যান্ডম ভেরিয়েবলের গড় মান। পাইথন বৈজ্ঞানিক কম্পিউটিং সম্পর্কিত প্যাকেজ ব্যবহার করে, আপনি সহজেই পারস্পরিক সম্পর্ক গণনা করতে পারেন।

তথ্য সংগ্রহ

এই নিবন্ধটি 2023 সালের পুরো বছরের জন্য Binance-এর 4hK লাইন ডেটা সংগ্রহ করে এবং 144টি মুদ্রা নির্বাচন করে যা 1 জানুয়ারিতে তালিকাভুক্ত করা হয়েছিল। নির্দিষ্ট ডাউনলোড ডেটা কোড নিম্নরূপ:

import requests
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

ticker = requests.get('https://fapi.binance.com/fapi/v1/ticker/24hr')
ticker = ticker.json()
sort_symbols = [k['symbol'][:-4] for k in sorted(ticker, key=lambda x :-float(x['quoteVolume'])) if k['symbol'][-4:] == 'USDT']

def GetKlines(symbol='BTCUSDT',start='2020-8-10',end='2023-8-10',period='1h',base='fapi',v = 'v1'):
    Klines = []
    start_time = int(time.mktime(datetime.strptime(start, "%Y-%m-%d").timetuple()))*1000 + 8*60*60*1000
    end_time =  min(int(time.mktime(datetime.strptime(end, "%Y-%m-%d").timetuple()))*1000 + 8*60*60*1000,time.time()*1000)
    intervel_map = {'m':60*1000,'h':60*60*1000,'d':24*60*60*1000}
    while start_time < end_time:
        time.sleep(0.5)
        mid_time = start_time+1000*int(period[:-1])*intervel_map[period[-1]]
        url = 'https://'+base+'.binance.com/'+base+'/'+v+'/klines?symbol=%s&interval=%s&startTime=%s&endTime=%s&limit=1000'%(symbol,period,start_time,mid_time)
        res = requests.get(url)
        res_list = res.json()
        if type(res_list) == list and len(res_list) > 0:
            start_time = res_list[-1][0]+int(period[:-1])*intervel_map[period[-1]]
            Klines += res_list
        if type(res_list) == list and len(res_list) == 0:
            start_time = start_time+1000*int(period[:-1])*intervel_map[period[-1]]
        if mid_time >= end_time:
            break
    df = pd.DataFrame(Klines,columns=['time','open','high','low','close','amount','end_time','volume','count','buy_amount','buy_volume','null']).astype('float')
    df.index = pd.to_datetime(df.time,unit='ms')
    return df

start_date = '2023-01-01'
end_date   = '2023-11-16'
period = '4h'
df_dict = {}

for symbol in sort_symbols:   
    print(symbol)
    df_s = GetKlines(symbol=symbol+'USDT',start=start_date,end=end_date,period=period)
    if not df_s.empty:
        df_dict[symbol] = df_s

df_close = pd.DataFrame(index=pd.date_range(start=start_date, end=end_date, freq=period),columns=df_dict.keys())
for symbol in symbols:
    df_s = df_dict[symbol]
    df_close[symbol] = df_s.close
df_close = df_close.dropna(how='any',axis=1)

বাজার পর্যালোচনা

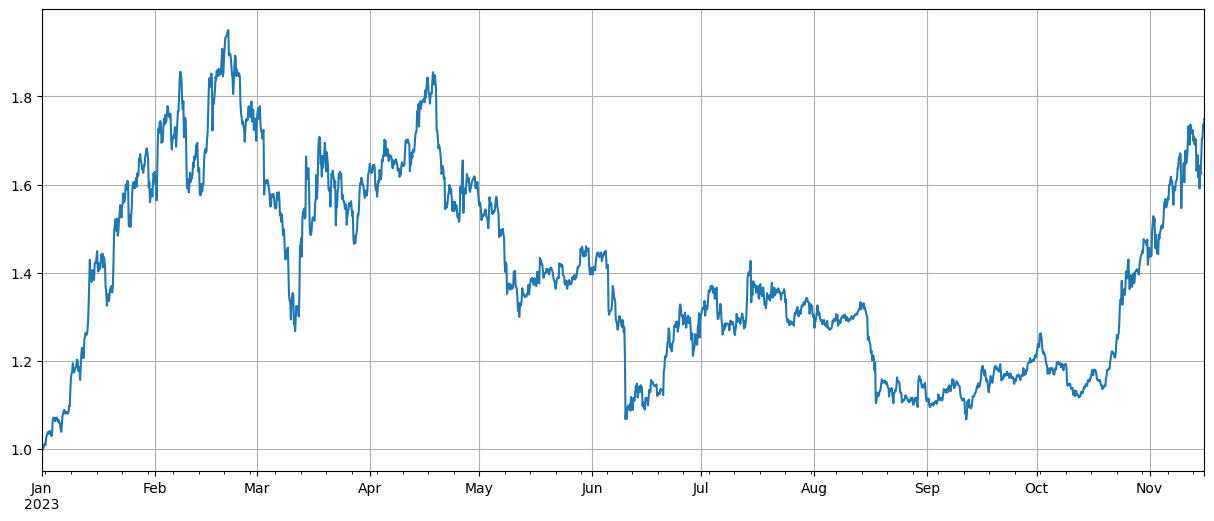
প্রথমত, ডেটা স্বাভাবিক করার পরে, গড় মূল্য বৃদ্ধি এবং পতনের সূচক গণনা করা হয় যে 2023 সালে বাজারের প্রবণতার দুটি তরঙ্গ থাকবে, যার মধ্যে বছরের শুরুতে একটি তীক্ষ্ণ বৃদ্ধি এবং অক্টোবর থেকে শুরু হওয়া তীক্ষ্ণ বৃদ্ধি। বর্তমানে, এটি মূলত উচ্চ সূচকে রয়েছে।

df_norm = df_close/df_close.fillna(method='bfill').iloc[0] #归一化
total_index = df_norm.mean(axis=1)
total_index.plot(figsize=(15,6),grid=True);

পারস্পরিক সম্পর্ক বিশ্লেষণ

পান্ডাগুলি বিটিসি মূল্যের সাথে সবচেয়ে দুর্বল পারস্পরিক সম্পর্ক রয়েছে, যার অর্থ হল তারা বিটিসি-এর মূল্য অনুসরণ করে, এটি ডিজিটালে একটি অসঙ্গতি মুদ্রা বাজার।

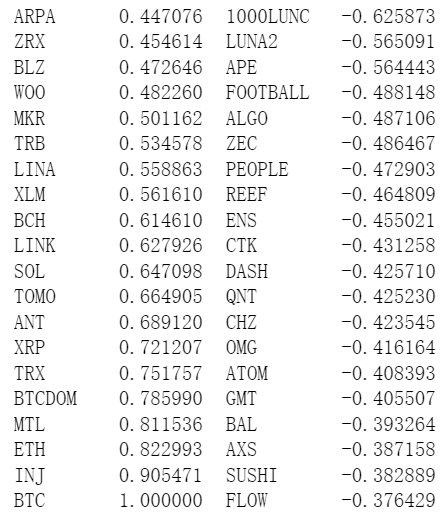
corr_symbols = df_norm.corrwith(df_norm.BTC).sort_values().index

পারস্পরিক সম্পর্ক এবং মূল্য বৃদ্ধি

এখানে আমরা মুদ্রাগুলিকে দুটি ভাগে ভাগ করি। প্রথম গ্রুপে ৪০টি মুদ্রা রয়েছে যা BTC মূল্যের সাথে সবচেয়ে বেশি সম্পর্কিত, এবং দ্বিতীয় গ্রুপে এমন মুদ্রা রয়েছে যা BTC মূল্যের সাথে সবচেয়ে কম সম্পর্কিত। দুটি গ্রুপের সূচক গড় দীর্ঘমেয়াদী মুদ্রার প্রতিনিধিত্ব করে। প্রথম গ্রুপে অবস্থান এবং দ্বিতীয় গ্রুপে সংক্ষিপ্ত অবস্থান। মূল্যের ওঠানামার মধ্যে সম্পর্ক এবং BTC-এর সাথে সম্পর্কের হিসাব করা যেতে পারে। কোড এবং ফলাফল নিম্নরূপ:

(df_norm[corr_symbols[-40:]].mean(axis=1)-df_norm[corr_symbols[:40]].mean(axis=1)).plot(figsize=(15,6),grid=True);

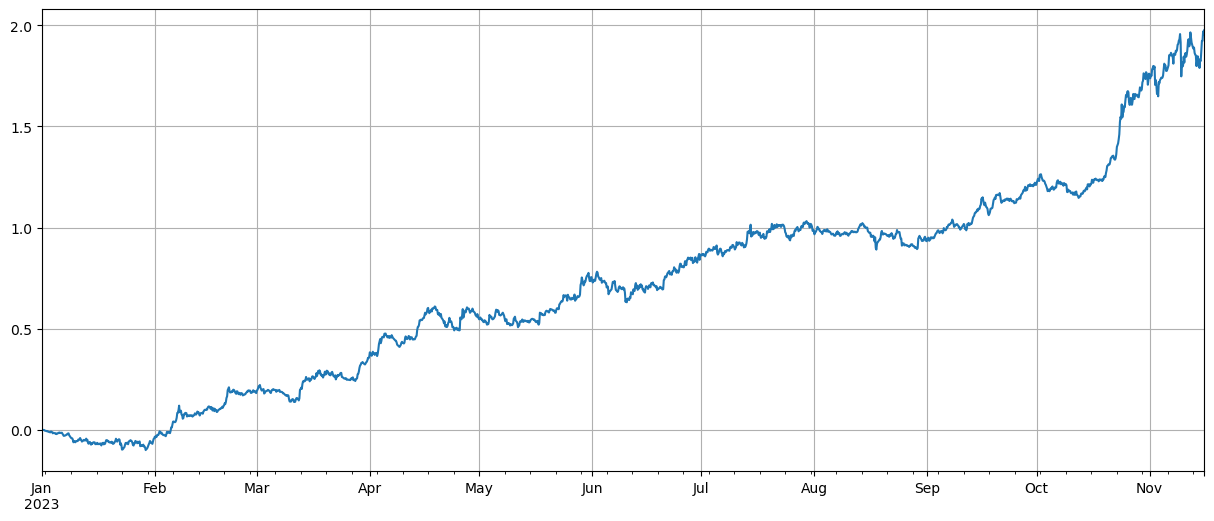
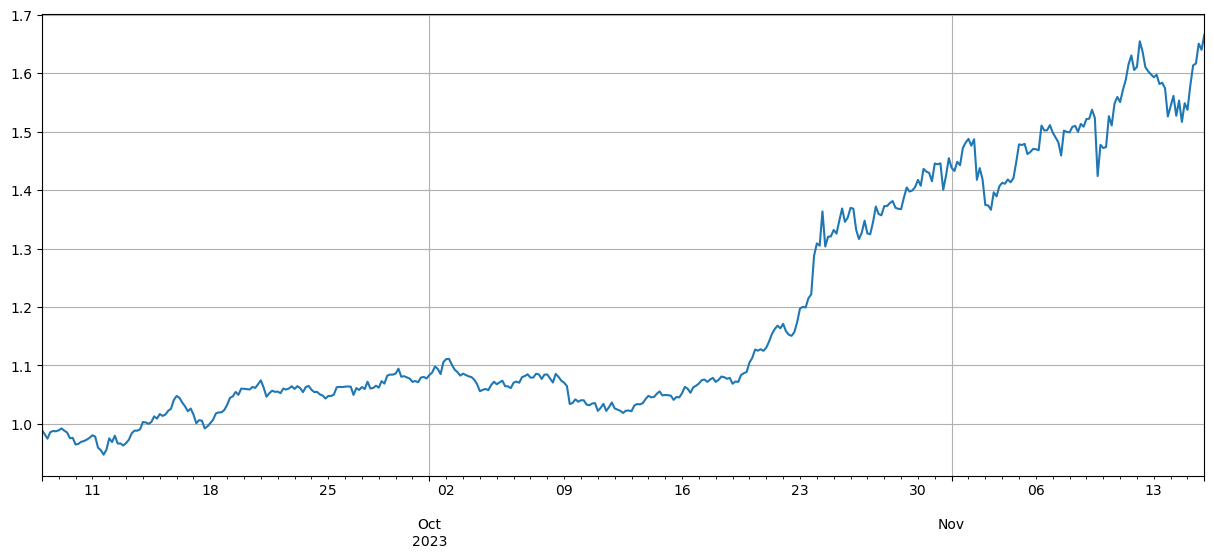
ফলাফলগুলি দেখায় যে বিটিসি দামের সাথে শক্তিশালী পারস্পরিক সম্পর্কযুক্ত মুদ্রাগুলির ভাল লাভ হয় এবং কম পারস্পরিক সম্পর্কের সাথে মুদ্রা ছোট করাও একটি ভাল হেজিং ভূমিকা পালন করে। এখানে যা কঠোর নয় তা হল ভবিষ্যতের ডেটাগুলিকে পরস্পর সম্পর্ক গণনা করার জন্য ব্যবহার করা হয়, ডেটা দুটি ভাগে ভাগ করা হয়, একটি দলকে পারস্পরিক সম্পর্ক গণনা করার জন্য ব্যবহার করা হয় এবং অন্য দলটি হেজিংয়ের পরে আয়ের হিসাব করতে ব্যবহৃত হয় নীচের চিত্রে দেখানো হয়েছে, এবং উপসংহার এখনও একই।

বাজারের নেতা হিসেবে, বিটকয়েন এবং ইথেরিয়ামের দামের ওঠানামা প্রায়শই সমগ্র বাজারের উপর বিশাল প্রভাব ফেলে। যখন এই বিটকয়েনের দাম বেড়ে যায়, তখন বাজারের মনোভাব সাধারণত আশাবাদী হয়ে ওঠে এবং অনেক বিনিয়োগকারী বাজারের প্রবণতা অনুসরণ করার প্রবণতা পোষণ করেন। বিনিয়োগকারীরা এটিকে পুরো বাজারের উত্থানের সংকেত হিসেবে দেখতে পারেন এবং অন্যান্য মুদ্রা কেনা শুরু করতে পারেন। বাজার অংশগ্রহণকারীদের সম্মিলিত আচরণের কারণে প্রধান মুদ্রার সাথে অত্যন্ত সম্পর্কিত মুদ্রাগুলির দাম একই রকম বৃদ্ধি পেতে পারে। এই সময়ে, মূল্য প্রবণতা সম্পর্কে বাজারের প্রত্যাশা কখনও কখনও একটি স্ব-পরিপূর্ণ ভবিষ্যদ্বাণীতে পরিণত হতে পারে। বিটকয়েনের সাথে নেতিবাচক সম্পর্কযুক্ত মুদ্রাগুলি অনন্য। এটা সম্ভব যে তাদের মৌলিক অবস্থার অবনতি হয়েছে অথবা তারা আর মূলধারার বিনিয়োগকারীদের দৃষ্টিতে নেই। এমনকি বিটকয়েনের জন্য একটি রক্তচোষা বাজারও থাকতে পারে - বাজার তাদের পরিত্যাগ করেছে। তারা লাভের সাথে তাল মিলিয়ে চলতে পারে এমন কয়েনগুলি তাড়া করুন।

corr_symbols = (df_norm.iloc[:1500].corrwith(df_norm.BTC.iloc[:1500])-df_norm.iloc[:1500].corrwith(total_index[:1500])).sort_values().index 

সারসংক্ষেপ

এই নিবন্ধের পিয়ারসন পারস্পরিক সম্পর্ক সহগ মুদ্রার মধ্যে পারস্পরিক সম্পর্কের মাত্রা প্রকাশ করে। নিবন্ধটি দেখায় কিভাবে মুদ্রার মধ্যে পারস্পরিক সম্পর্ক গণনা করতে ডেটা প্রাপ্ত করতে হয় এবং বাজারের প্রবণতা মূল্যায়ন করতে এই ডেটা ব্যবহার করতে হয়। এটি প্রকাশ করে যে ডিজিটাল মুদ্রার বাজারে দামের ওঠানামার সিঙ্ক্রোনিসিটি শুধুমাত্র বাজারের মনোবিজ্ঞান এবং কৌশলগুলির প্রতিফলন নয়, তবে বৈজ্ঞানিক পদ্ধতির মাধ্যমে পরিমাপ ও ভবিষ্যদ্বাণী করা যেতে পারে। এটি পরিমাণগত ট্রেডিং কৌশলগুলির নকশার জন্য বিশেষভাবে গুরুত্বপূর্ণ।

এই নিবন্ধে ধারণাগুলি সম্প্রসারণের জন্য অনেকগুলি ক্ষেত্র রয়েছে, যেমন ঘূর্ণায়মান পারস্পরিক সম্পর্ক গণনা করা, উত্থান এবং পতনের সময় পারস্পরিক সম্পর্ক গণনা করা ইত্যাদি এবং আরও কার্যকর তথ্য বিশ্লেষণ করা।