বায়েসিয়ান পরিসংখ্যান হল অর্থ, চিকিৎসা গবেষণা এবং তথ্য প্রযুক্তি সহ অনেক ক্ষেত্রে ব্যাপক প্রয়োগ সহ গণিতের একটি শক্তিশালী শৃঙ্খলা। এটি আমাদের পূর্ববর্তী বিশ্বাসগুলিকে প্রমাণের সাথে একত্রিত করে নতুন পরবর্তী বিশ্বাসগুলিতে পৌঁছানোর অনুমতি দেয়, যা আমাদের আরও সচেতন সিদ্ধান্ত নিতে দেয়।

এই নিবন্ধে আমরা সংক্ষেপে কিছু প্রধান গণিতবিদদের সাথে পরিচিত করব যারা এই ক্ষেত্রটি প্রতিষ্ঠা করেছিলেন।

বেইসের আগে বায়েসিয়ান পরিসংখ্যান আরও ভালভাবে বোঝার জন্য, আমাদের 18 শতকে ফিরে যেতে হবে এবং গণিতবিদ ডি মোইভরে এবং তার গবেষণাপত্র “দ্যা প্রিন্সিপল অফ চান্স”-এর উল্লেখ করতে হবে।[1]。

তার গ্রন্থে, ডি মোইভার তার সময়ের সম্ভাবনা এবং জুয়া সম্পর্কিত অনেক সমস্যার সমাধান করেছেন। আপনি সম্ভবত জানেন, এই সমস্যাগুলির একটিতে তার সমাধান স্বাভাবিক বিতরণের উত্সের দিকে পরিচালিত করেছিল, তবে এটি অন্য গল্প।

তার কাগজে একটি সহজ প্রশ্ন আছে:

“একটি ন্যায্য মুদ্রা টানা তিনবার ছুঁড়ে মারলে তিনটি মাথা পাওয়ার সম্ভাবনা।”

“দ্যা প্রিন্সিপল অফ চান্স”-এ বর্ণিত সমস্যাগুলি পড়লে আপনি লক্ষ্য করতে পারেন যে তাদের বেশিরভাগই একটি অনুমান দিয়ে শুরু করে এবং তারপরে এটি থেকে একটি প্রদত্ত ঘটনার সম্ভাব্যতা গণনা করে। উদাহরণস্বরূপ, উপরের সমস্যাটিতে, একটি অনুমান রয়েছে যে মুদ্রাটি ন্যায্য, তাই টসে হেড পাওয়ার সম্ভাবনা 0.5।

এটি আজ গাণিতিক পদে প্রকাশ করা হয়েছে:

𝑃(𝑋|𝜃)

কিন্তু যদি আমরা জানি না যে মুদ্রাটি ন্যায্য কিনা? যদি আমরা জানি না𝜃পশমী কাপড়?

টমাস বেইস এবং রিচার্ড প্রাইস

প্রায় পঞ্চাশ বছর পরে, 1763 সালে, “সম্ভাব্যের নীতিতে সমস্যার সমাধানের উপর একটি প্রবন্ধ” শিরোনামের একটি গবেষণাপত্র।[2] ফিলোসফিক্যাল লেনদেন, রয়্যাল সোসাইটি, লন্ডনে প্রকাশিত।

নথির প্রথম কয়েকটি পৃষ্ঠার মধ্যে গণিতবিদ রিচার্ড প্রাইসের লেখা একটি পাঠ্য রয়েছে যা তার মৃত্যুর কয়েক বছর আগে তার বন্ধু টমাস বেয়েসের লেখা একটি কাগজের বিষয়বস্তুর সংক্ষিপ্তসার করে। ভূমিকায়, প্রাইস টমাস বেইসের করা কিছু আবিষ্কারের গুরুত্ব ব্যাখ্যা করেছেন যেগুলি ডি মোইভারের দ্য প্রিন্সিপল অফ চান্সে অন্তর্ভুক্ত ছিল না।

আসলে, তিনি একটি নির্দিষ্ট সমস্যা উল্লেখ করছিলেন:

“একটি অজানা ঘটনা যতবার ঘটে এবং ব্যর্থ হয় তার সংখ্যার পরিপ্রেক্ষিতে, এটির সংঘটনের সম্ভাব্যতা সম্ভাব্যতার যেকোন দুটি নামযুক্ত ডিগ্রির মধ্যে রয়েছে।”

অন্য কথায়, একটি নির্দিষ্ট ঘটনা পর্যবেক্ষণ করার পরে, আমরা অজানা পরামিতিগুলি খুঁজে পাইθসম্ভাব্যতার দুই ডিগ্রির মধ্যে সম্ভাব্যতা কত। এটি আসলে ঐতিহাসিকভাবে পরিসংখ্যানগত অনুমানের সাথে যুক্ত প্রথম সমস্যাগুলির মধ্যে একটি ছিল এবং নামটি বিপরীত সম্ভাবনার দিকে পরিচালিত করেছিল। গাণিতিক ভাষায়:

𝑃( 𝜃 | 𝑋）

এটি অবশ্যই আজকে আমরা বায়েসের পোস্টেরিয়র ডিস্ট্রিবিউশনের উপপাদ্য বলে থাকি।

অকারণ কারণ

এই দুই প্রবীণ যাজকের সাথে পরিচিত হন,টমাস বেইসএবংরিচার্ড প্রাইস, গবেষণার জন্য অনুপ্রেরণা কি আসলে খুব আকর্ষণীয়. কিন্তু এটি করার জন্য, আমাদের একটি মুহুর্তের জন্য পরিসংখ্যান সম্পর্কে কিছু জ্ঞান সরাইয়া রাখা দরকার।

আমরা 18 শতকে আছি, এবং সম্ভাব্যতা গণিতবিদদের আগ্রহের ক্ষেত্র হয়ে উঠছে। De Moivre বা Bernoulli এর মতো গণিতবিদরা দেখিয়েছেন যে কিছু ঘটনা নির্দিষ্ট মাত্রার এলোমেলোতার সাথে ঘটে কিন্তু এখনও নির্দিষ্ট নিয়ম দ্বারা পরিচালিত হয়। উদাহরণস্বরূপ, আপনি যদি একাধিকবার একটি ডাই রোল করেন তবে ছয়টির মধ্যে একটি ছক্কায় ল্যান্ড করবে। এটা যেন একটা লুকানো নিয়ম আছে যা সুযোগের ভাগ্য নির্ধারণ করে।

এখন, কল্পনা করুন যে আপনি একজন গণিতবিদ এবং এই সময়ের মধ্যে বসবাসকারী একজন ধর্মীয় বিশ্বাসী। এই লুকানো নিয়ম ঈশ্বরের সাথে কীভাবে সম্পর্কিত তা জানতে আপনি আগ্রহী হতে পারেন।

এটি প্রকৃতপক্ষে বেইস এবং প্রাইস নিজেরাই প্রশ্ন করে। তারা এই সমস্যার সমাধান চেয়েছিলেন যা প্রমাণ করার জন্য সরাসরি প্রযোজ্য যে “জগৎ অবশ্যই জ্ঞান এবং বুদ্ধির প্রভাব; এবং তাই চূড়ান্ত কারণগুলির দ্বারা ঈশ্বরের অস্তিত্বের প্রমাণ প্রদান করুন”[2] - অর্থাৎ কারণ ছাড়া কারণ।

ল্যাপ্লেস

আশ্চর্যজনকভাবে, প্রায় দুই বছর পর 1774 সালে, স্পষ্টতই টমাস বেইসের গবেষণাপত্র না পড়েই, ফরাসি গণিতবিদ ল্যাপ্লেস “অন দ্য কজস অফ ইভেন্টস থ্রু দ্য প্রোবাবিলিটিস অফ ইভেন্টস” নামে একটি গবেষণাপত্র লিখেছিলেন।[3], যা বিপরীত সম্ভাবনা সমস্যার উপর একটি কাগজ। প্রথম পাতায় আপনি পড়তে পারেন

প্রধান নীতি:

“যদি কোন ঘটনা nটি ভিন্ন কারণে ঘটতে পারে, তাহলে একটি নির্দিষ্ট ঘটনার জন্য এই কারণগুলির সম্ভাব্যতা ঘটনার সম্ভাব্যতার সমান অনুপাতে কারণটি বিবেচনা করে, এবং এই প্রতিটি কারণের অস্তিত্বের সম্ভাবনা সমান।” কারণের উপর ভিত্তি করে ঘটনার সম্ভাব্যতা। কারণগুলির সম্ভাব্যতা, প্রতিটি কারণের উপর ভিত্তি করে ঘটনার সম্ভাব্যতার যোগফল দিয়ে ভাগ করলে।”

এটি আজকে আমরা বেইসের উপপাদ্য হিসাবে জানি:

​

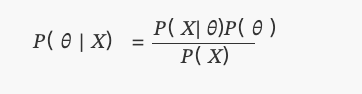
মধ্যেP(θ)সমানভাবে বিতরণ করা হয়।

মুদ্রা পরীক্ষা

আমরা পাইথন এবং PyMC লাইব্রেরি ব্যবহার করে বর্তমান সময়ে Bayesian পরিসংখ্যান আনব এবং একটি সাধারণ পরীক্ষা পরিচালনা করব।

ধরুন একজন বন্ধু আপনাকে একটি মুদ্রা দেয় এবং আপনাকে জিজ্ঞাসা করে যে আপনি এটি একটি ন্যায্য মুদ্রা কিনা। যেহেতু তিনি তাড়াহুড়ো করছেন, সে আপনাকে বলে যে আপনি মুদ্রাটি 10 ​​বার উল্টাতে পারবেন। আপনি দেখতে পাচ্ছেন, এই প্রশ্নে একটি অজানা পরামিতি রয়েছেp, একটি মুদ্রা টসে মাথা পাওয়ার সম্ভাবনা, এবং আমরা এটি অনুমান করতে চাইpএর সবচেয়ে সম্ভাব্য মান।

(দ্রষ্টব্য: আমরা প্যারামিটার বলতে চাই নাpএকটি এলোমেলো পরিবর্তনশীল, কিন্তু এই প্যারামিটারটি স্থির, এবং আমরা জানতে চাই কোন মানগুলির মধ্যে এটি মিথ্যা হওয়ার সম্ভাবনা সবচেয়ে বেশি। )

এই সমস্যাটিকে আলাদাভাবে দেখতে, আমরা দুটি ভিন্ন পূর্ব বিশ্বাসের অধীনে এটি সমাধান করব:

• ১. মুদ্রার ন্যায্যতা সম্পর্কে আপনার কোন পূর্ব তথ্য নেই এবং সমান সম্ভাব্যতা নির্ধারণ করুনp. এই ক্ষেত্রে, আমরা একটি তথ্যহীন পূর্ববর্তী ব্যবহার করব, কারণ আপনি আপনার বিশ্বাসে কোনও তথ্য যোগ করছেন না।

• 1. আপনি অভিজ্ঞতার মাধ্যমে জানেন যে যদিও একটি মুদ্রা অন্যায্য হতে পারে, এটিকে খুব অন্যায্য করা কঠিন, তাই আপনি মনে করেন প্যারামিটারগুলিpসম্ভবত এটি 0.3 এর কম বা 0.7 এর বেশি হবে না। এই ক্ষেত্রে আমরা একটি তথ্যমূলক পূর্বে ব্যবহার করব।

উভয় ক্ষেত্রেই, আমাদের পূর্বের বিশ্বাসগুলি নিম্নরূপ হবে:

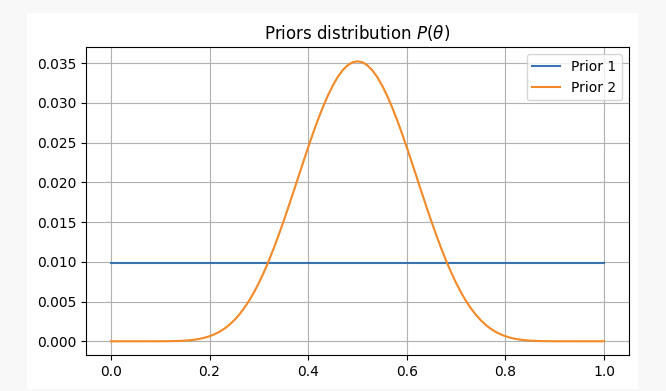
কয়েনটি 10 ​​বার টস করার পরে, আপনি 2টি মাথা পাবেন। এই প্রমাণের সাথে, আমরা সম্ভবত আমাদের পরামিতিগুলি খুঁজে পাব যেখানেp？

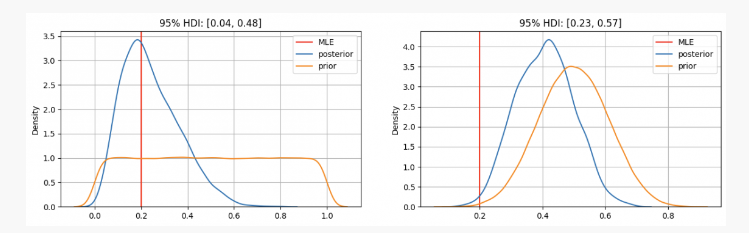
আপনি দেখতে পাচ্ছেন, প্রথম ক্ষেত্রে আমাদের প্যারামিটার আছেpএর পূর্ব বন্টন সর্বাধিক সম্ভাবনা অনুমান (MLE) এর উপর কেন্দ্রীভূতp=0.2, যা ঘন ঘন পদ্ধতি ব্যবহার করে একটি অনুরূপ পদ্ধতি। প্রকৃত অজানা প্যারামিটারটি 0.04 এবং 0.48 এর মধ্যে 95% আত্মবিশ্বাসের ব্যবধানের মধ্যে থাকবে।

অন্যদিকে, উচ্চ মাত্রার আত্মবিশ্বাস রয়েছে যে পরামিতিগুলিp 0.3 এবং 0.7 এর মধ্যে হওয়া উচিত, আমরা দেখতে পাচ্ছি যে পোস্টেরিয়র ডিস্ট্রিবিউশন প্রায় 0.4, আমাদের MLE যা দেয় তার থেকে অনেক বেশি। এই ক্ষেত্রে, প্রকৃত অজানা প্যারামিটারটি 0.23 এবং 0.57 এর মধ্যে 95% আত্মবিশ্বাসের ব্যবধানের মধ্যে থাকবে।

অতএব, প্রথম ক্ষেত্রে, আপনি আপনার বন্ধুকে বলবেন যে আপনি আত্মবিশ্বাসী যে মুদ্রাটি অন্যায়। কিন্তু অন্য পরিস্থিতিতে, আপনি তাকে বলবেন যে আপনি নিশ্চিত নন যে মুদ্রাটি ন্যায্য কিনা।

আপনি দেখতে পাচ্ছেন, এমনকি একই প্রমাণের সাথে (10 টি টসের মধ্যে 2 মাথা), বিভিন্ন পূর্ব বিশ্বাসের অধীনে ফলাফলগুলি ভিন্ন হবে। এটি বৈজ্ঞানিক পদ্ধতির অনুরূপ বায়েসিয়ান পরিসংখ্যানের একটি সুবিধা, যা আমাদের নতুন পর্যবেক্ষণ এবং প্রমাণের সাথে পূর্বের বিশ্বাসগুলিকে একত্রিত করে আমাদের বিশ্বাস আপডেট করতে দেয়।

END

আজকের নিবন্ধে আমরা বায়েসিয়ান পরিসংখ্যানের উত্স এবং এর প্রধান অবদানকারীদের দিকে তাকিয়েছি। তারপর থেকে, quantdare.com থেকে পুনরুত্পাদিত পরিসংখ্যানের এই ক্ষেত্রে (Jeffreys, Cox, Shannon, ইত্যাদি) আরও অনেক গুরুত্বপূর্ণ অবদানকারী রয়েছে৷