Delta-Hedging von Bitcoin-Optionen mithilfe der Smile Curve

Zusammenfassung

Wir analysieren die robuste dynamische Delta-Absicherung von Bitcoin-Optionen mithilfe einer Reihe impliziter Smile-Kurven und anderer Smile-bereinigter Deltas. Diese Deltas sind entweder modellfrei in dem Sinne, dass sie für jedes skaleninvariante stochastische und/oder lokale Volatilitätsmodell gleich sind, oder sie basieren auf einfachen, regimeabhängigen Parametrisierungen der lokalen Volatilität. Diese Deltas sind bei Market Makern auf Optionsmärkten für traditionelle Vermögenswerte beliebt, da sie einfach umzusetzen sind. Frühere empirische Untersuchungen zum dynamischen Delta-Hedging basierten ausschließlich auf Aktienindexoptionen. Die Analyse einzigartiger Daten zu stündlichen historischen Bitcoin-Optionspreisen zeigt jedoch, dass sich das Verhalten der impliziten Volatilitätskurve von Bitcoin stark von dem der Aktienindexoptionen unterscheidet. Für Call- und Put-Optionen mit einem breiten Finanzierungsuniversum und synthetischen festen Laufzeiten von 10, 20 und 30 Tagen vergleichen wir die dynamische Absicherungsperformance verschiedener Smile-adjustierter Deltas über zwei Einjahreszeiträume. Wir prüfen auch die Verwendung von unbefristeten Kontrakten anstelle von Standard-Futures als Absicherungsinstrument, da das Basisrisiko unbefristeter Kontrakte viel geringer ist als das von Kalender-Futures. Die Ergebnisse werden als überprüfbare Statistik des abgesicherten Fehlervarianzverhältnisses dargestellt. In manchen Zeiträumen kann die Verwendung des impliziten Smile-Curve-Hedge-Verhältnisses die einfache Black-Scholes-Delta-Absicherung deutlich übertreffen, insbesondere bei der Verwendung von Perpetual Swaps als Absicherungsinstrument kann der Effizienzgewinn von Out-of-the-Money-Put-Optionen 30 % übersteigen. Beim Absichern kurzfristiger, aus dem Geld liegender Call-Optionen in Zeiten steigender impliziter Volatilitätskurven können die durchschnittlichen Effizienzgewinne bis zu 15 % betragen. Die Vorteile unbefristeter Verträge zeigen sich im Jahr 2021 besonders bei langfristigen Verträgen, bei denen die Basis noch recht groß ist.

Schlagwörter ：Derivate-Hedging, implizite Volatilitätskurve, unbefristete Verträge, robuste Finanzierung, dynamische inkrementelle Absicherung

1. Einleitung

Sämtliche Forschungen zum dynamischen Delta-Hedging basieren auf dem Modell von Black und Scholes (1973). Für das Black-Scholes (BS)-Delta sind nur partielle Ableitungen des Modelloptionspreises nach dem Basispreis erforderlich, da das Modell davon ausgeht, dass die Korrelation zwischen dem Basispreis und seiner Volatilität Null beträgt. Es ist jedoch bekannt, dass Aktienindexoptionen eine große und negative Preis-Volatilitäts-Korrelation aufweisen, was zu einer erheblichen Schiefe der impliziten Volatilitätskurve führt. Nach der Grundidee von Bates (2005) und den allgemeineren Ergebnissen von Alexander und Nogueira (2007a) kann die Steigung der impliziten Volatilitätskurve verwendet werden, um Anpassungen an das BS-Delta zu implizieren, was modellfrei ist, d. h. es ist für alle skalenunabhängigen Modelle konstant. Die Variantenmodelle sind dieselben. Alexander und Nogueira (2007b) zeigen jedoch, dass für handelbare Instrumente (außer Zinssätzen) jedes stochastische und/oder lokale Volatilitätsmodell zur Aktienoptionspreisbildung skaleninvariant sein sollte, unabhängig von zusätzlichen Faktoren wie Sprüngen oder Lévy-Prozessen. Wie komplex die Funktionen sind. Daher ist jeder Unterschied zwischen der empirischen Absicherungsleistung der beiden parametrischen Volatilitätsmodelle (für handelbare Instrumente) lediglich darauf zurückzuführen, dass die Modelle unterschiedliche Kalibrierungsfehler aufweisen. Die partielle Ableitung des Deltas (eigentlich Gammas) des Optionspreises in Bezug auf den Preis des handelbaren Instruments ist theoretisch genau dasselbe wie das modellfreie, skaleninvariante Delta. Anmerkung 1: Darüber hinaus ist das von Bates (2005) vorgeschlagene einfache skaleninvariante Delta größer (kleiner) als das BS-Delta, wenn die Steigung der Smile-Kurve negativ (positiv) ist. Da Coleman et al. (2001) zeigen, dass das BS-Delta in einem lokalen Volatilitätsrahmen dazu neigt, übersichert zu sein, wird das skaleninvariante Delta bei einer negativen Schiefe der impliziten Volatilität stärker übersichert sein als das BS-Delta.

Wie von Alexander und Nogueira (2007a) beschrieben, ist die minimale Varianz (MV) der Gesamtableitung in Bezug auf den Preis ein weiteres Delta, das von Null verschiedene Preis-Volatilitäts-Korrelationen berücksichtigt, es ist jedoch modellabhängig. Diesen Autoren gelang es jedoch nicht, zwischen den empirischen Ergebnissen, die mit dem modellfreien MV Delta von Lee (2001) erzielt wurden, und den MV Deltas zu unterscheiden, die auf anderen skaleninvarianten Modellen basieren. Das MV Delta von Lee (2001) ist ebenfalls „smile-bereinigt“, d. h. es fügt dem BS-Delta einen Term hinzu, der mithilfe der empirischen Charakteristika der impliziten Volatilitäts-Smile-Kurve kalibriert wird. Eine andere Möglichkeit zum Anpassen des BS-Deltas besteht darin, den in der bahnbrechenden Arbeit „Smile-Adjusted Delta“ von Derman und Kani (1994) und Derman (1999) vorgeschlagenen Ansatz zu verwenden, indem ein Term hinzugefügt wird, der die Preis-Volatilitäts-Korrelation erfasst. Diese sind nicht völlig modellfrei, da der Anpassungsterm von der Parametrisierung der lokalen Volatilität abhängt, die wiederum vom vorherrschenden Marktregime abhängt. Sie sind jedoch modellfrei, da keine Annahmen über die Prozesse getroffen werden, die die Entwicklung des zugrunde liegenden Preises vorantreiben, wie z. B. die stochastische lokale Volatilitätssprungdiffusion, und es gibt keine Parameter, die mithilfe von Optionspreisen und/oder zugrunde liegenden historischen Daten.

Für Market-Maker von Aktienoptionen ist es gängige Praxis, ihre Engagements mithilfe einfacher, modellfreier Anpassungen des BS-Deltas abzusichern, da diese als sogenannte „robuste Finanzierung“ gelten, d. h. die Hedge-Ratio ist modellunabhängig. Implizite Smile-Kurven und andere Smile-Adjusted-Curve-Adjusted-Delta-Hedges erfreuen sich unter Praktikern besonderer Beliebtheit, wie zahlreiche Artikel und Foren belegen. Anmerkung 2: Es gibt mehrere frühere empirische Studien zum Delta-Hedging impliziter Smile-Kurven und/oder Smile-adjustierter Kurven, aber sie alle untersuchten Aktienindexoptionen. Nicht alle Ergebnisse sind konsistent: Vähämaa (2004) zeigt, dass einige Smiling-Curve-adjustierte Deltas die BS-Deltas für FTSE-100-Optionen übertreffen, aber nur in Zeiten übermäßiger Volatilität; Crépey (2004) bestätigt, dass diese Ergebnisse für DAX-30-Optionen gelten; Attie ( 2017) behauptet, dass das Smile-implizierte Delta das BS-Delta bei der Absicherung von S&P 500-Indexoptionen durchgängig übertrifft; Alexander et al. (2012) erweitern Dermans (1999) Rahmen auf eine Markov-Switching-Einstellung. um das korrekte Smile-adjustierte Delta widerzuspiegeln, das auf die aktuelle Marktregime, was zeigt, dass für S&P 500-Optionen BS Delta nur durch die Verwendung dieser Markov-Switching-Erweiterung verbessert werden kann; François und Stentoft (2021) untersuchten auch die S&P 500-Indexoptionen und bestätigen, dass Standardanpassungen BS Delta oder Delta-Gamma nicht übertreffen können Hedges, aber ihr neuer impliziter Smiling-Curve-Delta-Gamma-Vega-Hedge verbessert das BS-Modell erheblich. Über den Erfolg von Smile-Adjusted Delta Hedging im Vergleich zu anderen Optionsarten ist wenig bekannt. Anmerkung 3

Der Zweck dieses Dokuments besteht darin, die Delta-Hedging-Leistung verschiedener Smile-implizierter Kurven und anderer Smile-bereinigter Kurven zu untersuchen, die auf Bitcoin-Optionen angewendet werden. Zum Zeitpunkt des Schreibens dieses Artikels gibt es nur wenige Forschungsarbeiten zu Bitcoin-Optionen. Siu und Elliott (2021), Jalan et al. (2021) sowie Chen und Huang (2021) untersuchen allesamt die empirischen Anwendungen stochastischer Volatilitätspreismodelle, aber keine der Arbeiten untersucht deren Absicherungsleistung. Hou et al. (2020) betrachteten eine Reihe stochastischer Volatilitätsmodelle zur Preisbestimmung von Bitcoin-Optionen. Die Autoren präsentieren eine Reihe wichtiger Ergebnisse, die die Bedeutung von Sprüngen und Co-Sprüngen hervorheben, und schlagen ein stochastisches Volatilitätsmodell mit korrelierten Sprüngen (SVCJ) zur Preisbestimmung von Bitcoin-Optionen vor. Diese Modelle sind sehr nützlich für die Preisgestaltung exotischer Optionen wie Cliquet- oder Ratchet-Optionen. Obwohl Chi und Hao (2021) GARCH-basierte Delta-Hedging-Strategien betrachten, konzentriert sich ihre Forschung auf den Vergleich verschiedener Modelle zur Prognose der realisierten Volatilität. Alexander et al. (2022b) untersuchen das Verhalten der impliziten Volatilitäts-Smile-Kurve für Bitcoin-Optionen, um daraus zu schließen, ob der Nachfragedruck der Market Maker von Richtungs- oder Volatilitätshändlern getrieben wird. Tatsächlich gibt es unseres Wissens nach nur eine weitere detaillierte Studie zur Absicherung von Bitcoin-Optionen (Matic et al., 2021), und diese verwendet einen völlig anderen Ansatz als dieses Dokument. Matic et al. (2021) verwenden die täglich von der Deribit-Börse angegebene implizite Volatilität, um die von der parametrischen stochastischen Volatilität inspirierte implizite Volatilitätsoberfläche zu kalibrieren und dann die implizite Volatilität von Optionen zwischen einem und drei Monaten arbitragefrei zu interpolieren. Volatilität. Die Stichprobe zwischen April 2019 und März 2020 wird dann unter Verwendung des von Duffie et al. (2000) und McNeil und Frey (2000) eingeführten stochastischen Volatilitätsprozesses in drei Unterperioden (Bullenmarkt, ruhiger Markt und COVID-Periode) unterteilt. GARCH-Filterkerneldichte zur Modellierung der zugrunde liegenden Kryptowährungspreise. Anschließend vergleichen sie die Hedge-Performance der BS Greeks mit der Performance verschiedener stochastischer Volatilitäts-Jump-Diffusion-Modelle. Bei Optionen mit einer Laufzeit von einem Monat stellen die Autoren keine signifikanten Verbesserungen gegenüber der einfachen BS-Absicherung fest. Bei Optionen mit einer Laufzeit von drei Monaten verbessern komplexere Modelle die Absicherungsleistung jedoch erheblich.

Anders als Matic et al. (2021) vergleichen wir nicht die Optionsabsicherungsperformance verschiedener stochastischer Volatilitätsmodelle. Ein wichtiger praktischer Vorteil unserer Studie ist, dass alle Delta-Werte sehr einfach zu berechnen sind. Da alle Informationen direkt und robust modellfrei aus der Volatilitäts-Smile-Kurve abgeleitet werden, ist keine Modellkalibrierung erforderlich. Ergebnisse unserer Delta-Absicherung unter Verwendung verschiedener BS-Delta-Anpassungen, die von den aktuellen Marktbedingungen, der Form des impliziten Volatilitäts-Smiles und/oder der Preis-Volatilitäts-Korrelation abhängen.

Unser Fokus liegt auf kurzfristigen Optionen mit Laufzeiten von 10 bis 30 Tagen, die eine viel höhere Liquidität und eine größere Bandbreite an Ausübungspreisen aufweisen als die in Matic et al. (2021) untersuchten Optionen. Wir haben uns für diese Vorgehensweise entschieden, weil Bitcoin-Optionen mit Verfallsdaten zwischen einem und drei Monaten nur 20 % des gesamten Handelsvolumens ausmachen, während Optionen mit Verfallsdaten von 30 Tagen oder weniger 50 % des gesamten Handelsvolumens ausmachen. Etwa 80 % aller Handelsvolumen. Darüber hinaus benötigen wir eine geeignete Smile-Kurve, um das BS-Delta an das Smiley-Prinzip anzupassen, und die Liquid-Strike-Range dieser kurzfristigen Optionen ist ziemlich groß. Tatsächlich liegt die Geldmäßigkeit der in unserer empirischen Analyse verwendeten Optionen zwischen 0,7 und 1,3.

Wir betrachten nur dynamisches Delta-Hedging mit regelmäßiger Neugewichtung, die alle acht Stunden zum Finanzierungszeitpunkt oder täglich um 00:00 UTC erfolgt. Die Wahl dieses Versuchsdesigns basiert auf den Eigenschaften des Bitcoin-Optionsmarktes, die neuartig sind und daher später ausführlich erläutert werden. Die Transaktionskosten von Futures sind wesentlich geringer als die von Optionen. Beispielsweise liegen die Spreads von Futures-Kontrakten je nach Verfallsdatum zwischen 1 und 5 Basispunkten, während kurzfristige At-the-Money-Optionen, die häufig für die Gamma-Absicherung verwendet werden, typischerweise Spreads von etwa 200 bis 300 Basispunkten aufweisen. Punkte. Daher ist Gamma-Hedging viel teurer als herkömmliches dynamisches Delta-Hedging. Die Transaktionskosten für die Neugewichtung eines Gamma-Hedges können den durch die Reduzierung des Hedge-Fehlers erzielten Gewinn schmälern, wohingegen die Transaktionskosten für die Neugewichtung eines Delta-Hedges gering sind, insbesondere wenn unbefristete Verträge als Absicherungsinstrument verwendet werden.

Als nächstes beschreibt Abschnitt 2 den Markt für Bitcoin-Optionen und -Futures; Abschnitt 3 vergleicht die Eigenschaften der impliziten Volatilitätsoberflächen für Bitcoin und Aktienindizes und unterscheidet ihre Merkmale; Abschnitt 4 beschreibt unseren empirischen Rahmen. Jedes Hedge-Verhältnis wird als angepasste BS-Formel eingeführt ; Abschnitt 5 beschreibt unsere Daten; Abschnitt 6 stellt die empirischen Ergebnisse vor; und Abschnitt 7 schließt.

2. Bitcoin-Options- und Terminmärkte

Zum Zeitpunkt des Schreibens dieses Artikels bieten sechs große Kryptowährungsbörsen den Optionshandel mit Bitcoin und anderen Währungen sowie einigen Token an, wobei das durchschnittliche tägliche Handelsvolumen im Dezember 2021 fast 1 Milliarde US-Dollar betrug. Insbesondere das Handelsvolumen bei Bitcoin-Optionen hat in letzter Zeit ein Allzeithoch erreicht: Das durchschnittliche monatliche Handelsvolumen hat sich mehr als verdoppelt und das offene Interesse hat sich von Januar 2020 bis Dezember 2021 mehr als versechsfacht. Der überwiegende Teil des Handels wird an der Optionsbörse Deribit abgewickelt, die ihren Sitz nach Panama verlegt hat, um internationalen Standards staatlicher Behörden wie der US-amerikanischen Commodity Futures Trading Commission (CFTC) oder anderen Regulierungsformen zum Schutz der Kundeninteressen zu entgehen. Wie viele andere unregulierte Börsen für Kryptowährungsderivate, die oft in Offshore-Steueroasen registriert sind, ist die Handelsplattform von Deribit rund um die Uhr geöffnet und hält sich kaum bis gar nicht an „Know Your Customer“-Protokolle. Im Jahr 2020 wurden auf Deribit 4,3 Millionen Kontrakte (mit einem Nominalwert von rund 55 Milliarden US-Dollar) gehandelt, und im Jahr 2021 waren es 6,2 Millionen Kontrakte (mit einem Nominalwert von rund 290 Milliarden US-Dollar). Infolgedessen ist die Anzahl der gelisteten Kontrakte in nur zwei Jahren um mehr als 45 % gestiegen und der auf Deribit gehandelte Nominalbetrag hat um mehr als 430 % zugenommen. Anmerkung 4: Um dies ins rechte Licht zu rücken: Der S&P 500-Optionsmarkt der Chicago Board Options Exchange (CBOE) wuchs zwischen 2020 und 2021 nur um etwa 10 %. Anmerkung 5: Auf dem Bitcoin-Optionsmarkt werden fast jeden Monat neue Kontraktgrößen, breitere Ausübungspreisspannen, längere Laufzeiten und neue Basiswerte veröffentlicht, wodurch dieser aufstrebende Derivatemarkt sowohl für Privat- als auch für institutionelle Händler zugänglich wird. Bitcoin-Optionen sind damit nicht mehr nur ein Nischenprodukt. . Im März 2022 führte die Chicago Mercantile Exchange (CME) Mikro-Bitcoin-Optionen ein, um mit selbstregulierten Plattformen zu konkurrieren, die sich an Privatanleger richten. Aber auch große institutionelle Akteure beobachten den Optionsmarkt sehr genau, manche sprechen sogar davon, dass es sich um den „nächsten großen Schritt“ handelt. Anmerkung 6: Andererseits bieten aufkommende dezentrale Finanzprotokolle (DeFi) wie Opyn oder Ribbon Finance den Optionshandel an, ohne dass dabei irgendwelche gesetzlichen Vorschriften eingehalten werden müssen. Mit einem nominellen Handelsvolumen von über 500 Millionen US-Dollar pro Tag ist dies kein Markt mehr, den traditionelle Anleger ignorieren können.

Das schiere Handelsvolumen auf Deribit macht es zur attraktivsten Börse für jede Art der Recherche von Kryptowährungsoptionen. Obwohl CME (und einige andere Börsen) nur Bitcoin-Optionen listen, können nur 10–15 % des Handelsvolumens mit Bitcoin-Optionen diesen Börsen zugeschrieben werden. Allein auf Deribit entfallen über 90 % des Handelsvolumens für Bitcoin-Optionen. Anmerkung 7: Ein Grund könnte sein, dass Deribit rund um die Uhr in Betrieb ist, während CME nur an Wochentagen aktiv ist. Ein weiterer Grund könnte sein, dass Deribit-Optionen in Bitcoin besichert und abgerechnet werden, obwohl ihnen der USD-Wert des BTC-Index zugrunde liegt. Um die Auszahlung bei Verfall zu erhalten, wird die Differenz zwischen dem BTC-Wert in USD und dem Ausübungspreis der Option (ebenfalls in USD angegeben) berechnet und das Ergebnis unter Verwendung des BTC-Indexwerts bei Verfall in Bitcoin umgerechnet. Anmerkung 8: Die Differenz in den Währungseinheiten zwischen dem Abrechnungspreis (z. B. Bitcoin) und dem Basiswert (z. B. USD) ist der Auszahlung einer Quanto-FX-Option sehr ähnlich, mit der Ausnahme, dass es keine Futures oder Optionen in die entgegengesetzte Richtung gibt. Das heißt, es gibt weder Derivate auf den Wert eines Dollars in Bitcoin noch Optionen, die den Wert eines Dollars in Bitcoin als Basiswert verwenden. Aus diesem Grund werden Bitcoin-Optionen auch „inverse Optionen“ genannt und sind tatsächlich nur eines von mehreren inversen Derivatprodukten, einschließlich inverser Futures, die an vielen Börsen für Kryptowährungsderivate in großem Umfang gehandelt werden. Sie sind attraktiv, weil der Derivatehandel mit Fiat-Kryptowährungen durchgeführt werden kann, ohne dass Fiat-Währungen als Sicherheiten auf einem Margin-Konto oder zur Vertragsabwicklung verwendet werden müssen.

Ob Bitcoin als Geldmarkt im herkömmlichen Sinne existieren kann, ist umstritten (Sauer, 2016), aber es gibt in vielen Farming-Sites und verschiedenen Liquiditätspools hochaktive dezentrale Geldmärkte für Bitcoin (und andere Währungen und Token). Anmerkung 9: Wir können daher von USD in Bitcoin umrechnen, um die Absicherungswirkung jedes Modells in USD zu messen.

Unabhängig davon, für welche Absicherungsmethode Sie sich entscheiden, ist die Absicherung selbst einfach. Der Händler eröffnet eine Position in einer Option und nimmt eine entgegengesetzte Position im Basiswert mit einer Positionsgröße ein, die dem Deltawert der Option entspricht. Auf traditionellen Märkten ist das Absicherungsinstrument üblicherweise ein Terminkontrakt mit der gleichen Laufzeit wie die Option, da der Abrechnungspreis kein leicht handelbares Instrument ist. Für den BTC-Index gelten die gleichen Kommentare, da er auf einem Durchschnittswert der Bitcoin-Preise mehrerer verschiedener Börsen basiert. Dies bedeutet jedoch nicht, dass das Absicherungsinstrument ein inverser Terminkontrakt mit der gleichen Laufzeit wie die Option sein muss, da es bei der Auswahl handelbarer Absicherungsinstrumente für Bitcoin einige innovative Alternativen gibt. Erstens gibt es drei verschiedene Arten von Futures-Kontrakten mit begrenzter Laufzeit: Standard-Linear-Futures, die sich nicht von Futures auf traditionelle Anlageklassen unterscheiden; Linear-Futures auf Bitcoin gegen USD-Stablecoins (wie Tether), die gehandelt werden, wenn der Preis des Stablecoins weicht von seiner USD-Bindung ab; , was ein Basisrisiko mit sich bringt; und inverse Futures, die ähnliche Eigenschaften wie lineare USD-Futures haben, aber wie Kryptowährungen mit Beträgen belegt und abgewickelt werden. Anmerkung 10

Bitcoin-Optionen verfügen außerdem über ein Absicherungstool, das auf Verträgen basiert, die einzigartig für den Kryptowährungsmarkt sind. Solche Verträge werden oft als Perpetual Futures, Perpetual Swaps oder einfach „Perpetual Contracts“ bezeichnet und sind die mit Abstand beliebteste Art von Kryptowährungsderivaten. Ihre Preise sind eng an den Spotpreis gekoppelt und nutzen einen „Finanzierungsmechanismus“, der alle acht Stunden automatisch einen kleinen Teil der Nettoposition auszahlt oder erhält. Die Berechnung dieses Prozentsatzes, der als „Finanzierungsrate“ bezeichnet wird, variiert von Börse zu Börse. Anmerkung 11: Zahler und Empfänger hängen davon ab, ob der Preis des unbefristeten Vertrags höher oder niedriger als der Spotpreis (BTC) ist. Wenn der Preis des unbefristeten Vertrags über dem Kassapreis liegt, ist der Finanzierungssatz positiv und Benutzer mit Long-Positionen in unbefristeten Verträgen müssen Gebühren zahlen, während Benutzer mit Short-Positionen Gebühren erhalten. Das Gegenteil ist der Fall, wenn der Preis des unbefristeten Vertrags niedriger ist als der Spotpreis. Regelmäßige Finanzierungszahlungen zwischen Long- und Short-Positionen halten den Preis des unbefristeten Vertrags sehr nahe am Kassapreis.

Auf Binance, der weltweit größten Spot- und Derivatebörse für Kryptowährungen, sind zwei Drittel der Handelsprodukte unbefristete Terminkontrakte. Dieses Verhältnis zwischen Spot und Derivaten scheint auf dem Kryptowährungsmarkt Standard zu sein, wie der CryptoCompare-Bericht (2022) zeigt. Zum Zeitpunkt der Abfassung dieses Artikels melden acht Kryptowährungsbörsen ein durchschnittliches tägliches Handelsvolumen mit Futures von über einer Milliarde Dollar, wobei der Großteil davon auf unbefristete Kontrakte zurückzuführen ist. Anmerkung 12: Hier machen unregulierte Börsen wie Binance, OKEx und Bybit mehr als 65 % des gesamten Futures-Handels aus. Im Gegensatz dazu haben regulierte Börsen, insbesondere CME und FTX US, einen viel geringeren Marktanteil von etwa 25 %. Deribit-Futures weisen ein durchschnittliches tägliches Handelsvolumen von über 4 Milliarden US-Dollar auf und verfügen damit über genügend Liquidität, um diese Futures als geeignete Absicherungsinstrumente zu betrachten. Wie an anderen Börsen auch, wird der Großteil des Handels allerdings mit unbefristeten Kontrakten und nicht mit Kalender-Futures abgewickelt. Um dies zu verdeutlichen, zeigt Abbildung 1 die nominellen Handelsbeträge dieser Kontrakte, die täglich aufgezeichnet, jedoch mithilfe eines gleitenden 7-Tage-Durchschnitts über einen Zeitraum von zwei Jahren ab Januar 2020 geglättet wurden. Es ist klar, dass unbefristete Futures-Kontrakte ein weitaus größeres Volumen aufweisen als Futures mit begrenzter Laufzeit, obwohl wir für Letztere tägliche Volumendaten für alle drei Futures-Typen sowie Daten für jedes Verfallsdatum aggregiert haben. . Im Jahr 2021 hat sich das Handelsvolumen für unbefristete Kontrakte im Vergleich zum Vorjahr fast vervierfacht. Tabelle 1 veranschaulicht diese Entwicklung der Handelsvolumina empirisch. Es zeigt das durchschnittliche tägliche Volumen und das offene Interesse für drei wichtige Bitcoin-Derivate an der Deribit-Börse. Die Volumina und das offene Interesse über alle Produkte hinweg stiegen zwischen 2020 und 2021 deutlich an, was höchstwahrscheinlich auf das Interesse großer Banken und Eigenhandelsunternehmen am Krypto-Bereich zurückzuführen ist.

Abbildung 1. Durchschnittliches tägliches Handelsvolumen von Deribit-Futures und unbefristeten Kontrakten.

Abbildung 1 zeigt das durchschnittliche Tagesvolumen der unbefristeten Kontrakte (blau) und das durchschnittliche Gesamtvolumen aller anderen Futures-Kontrakte (rot) von Januar 2020 bis Januar 2022. Das tägliche Volumen wird berechnet, indem die Gesamtzahl der auf Deribit innerhalb von 24 Stunden gehandelten Kontrakte mit ihrem Nominalwert von 10 US-Dollar multipliziert und anschließend der Durchschnitt der letzten sieben Tage ermittelt wird. Die Ergebnisse liegen in Milliarden US-Dollar.

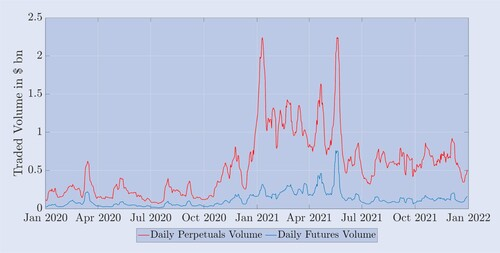
Tabelle 1. Volumen und offenes Interesse von Deribit-Bitcoin-Derivaten.

3. Implizite Volatilität von Bitcoin

Abbildung 2 veranschaulicht die empirische Dynamik der impliziten Volatilitätskurve, die aus Deribit-Optionen abgeleitet wurde, aufgetragen über einen Zeitraum von zweieinhalb Jahren in einer Tagesstruktur. Die Moneyness-Achse stellt die Volatilitätskurve dar, die sich aus dem Preis von Call-Optionen aus dem Geld zu Put-Optionen aus dem Geld ergibt. Die Moneyness von Put-Optionen, die tief aus dem Geld liegen, beträgt 0,7, die Die Moneyness von tief aus dem Geld liegenden Call-Optionen beträgt 1,3 und die Moneyness von am Geld liegenden Optionen beträgt 1,3. Sowohl Call- als auch Put-Optionen haben eine Moneyness von 1, und wir interpolieren die Daten, um diese Moneyness-Levels darzustellen bei eine feste Ablauffrist von 30 Tagen. Weitere Einzelheiten zu den Daten und ihrer Filterung finden Sie im nächsten Abschnitt.

Abbildung 2. Implizite Volatilitätskurve von Bitcoin.

Die implizite Volatilitätskurve für Bitcoin-Optionen mit einer konstanten Verfallsperiode von 30 Tagen, die tägliche Daten vom 1. Januar 2020 bis zum 30. Juni 2022 abdeckt, abgeleitet aus Out-of-the-Money- und At-the-Money-Optionen. . Die Ausübungspreise liegen zwischen 30 % unter und 30 % über dem aktuellen zugrunde liegenden Bitcoin-Indexwert.

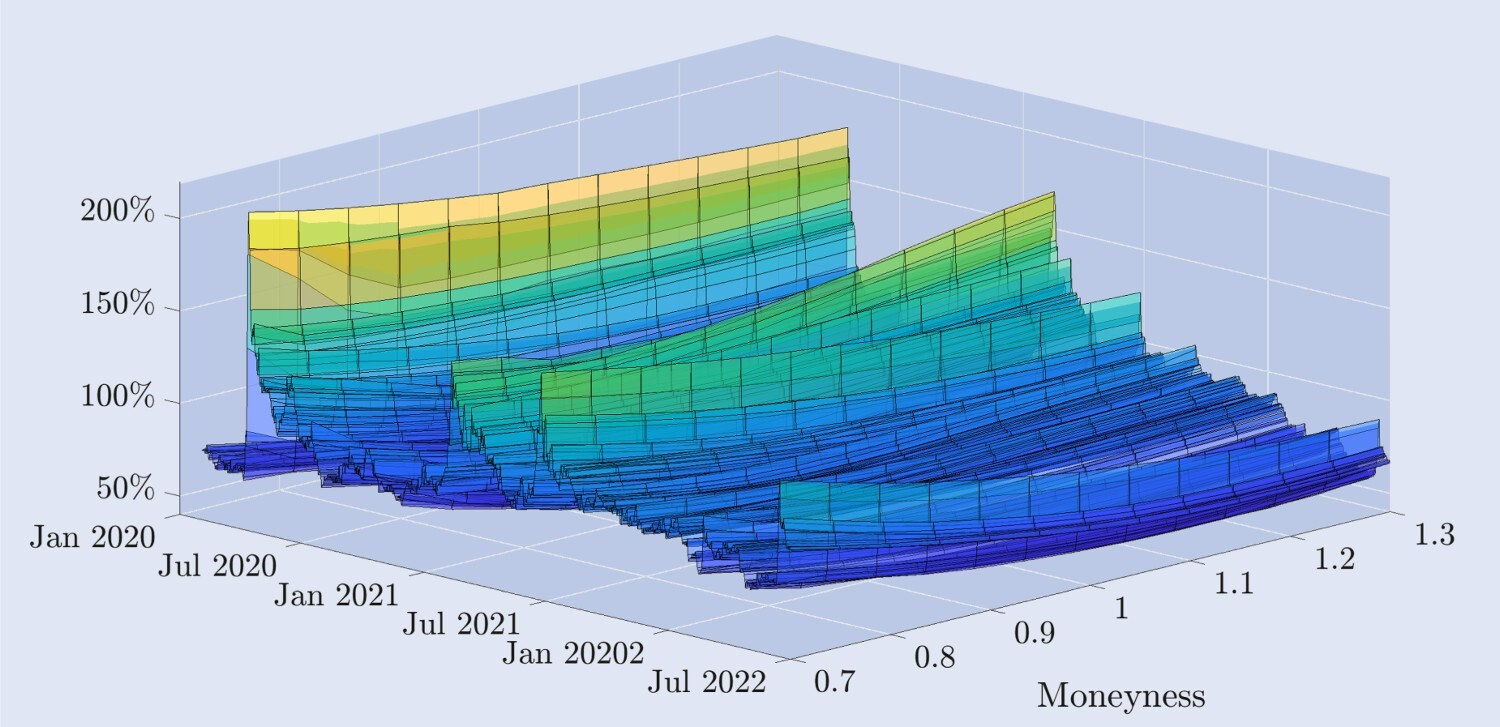
Die Form der Kurve variiert im Laufe der Zeit erheblich. Kurz nach dem „Schwarzen Donnerstag“ im März 2020, als der Bitcoin-Preis innerhalb weniger Stunden um mehr als 30 % fiel, nahm die implizite Volatilitätskurve eine negativ verzerrte Form an, die typisch für Aktienindexoptionen ist. Das heißt, Die Volatilität von Out-of-the-Money-Put-Optionen ist viel höher als die von Out-of-the-Money-Call-Optionen. Allerdings weisen Bitcoin-Optionen im Allgemeinen eine viel höhere implizite Volatilität auf als Aktienindexoptionen. Während des größten Teils des Beobachtungszeitraums weist die Kurve der impliziten Volatilität die Form eines „Hockeyschlägers“ auf, während sie in besonders ruhigen Zeiten zu einer leicht symmetrischen Lächelnkurve abflacht. Es gibt auch Fälle positiver Schiefe, bei denen die Volatilität von Out-of-the-Money-Calls viel höher ist als die von Out-of-the-Money-Puts. Diese Merkmale sind auf dem Markt für Aktienindexoptionen nicht üblich; dort wird zur Beschreibung häufig der Begriff „Skew“ (Schiefe) und nicht „Smile“ (Lächeln) verwendet. Zur Untermauerung dieser Annahme bietet Abbildung 3 eine andere Ansicht des impliziten Volatilitäts-Smiles. Es zeigt die implizite Volatilität von Bitcoin bei verschiedenen Geldmengenniveaus (oberes Diagramm) sowie die Abweichung von der Volatilität am Geldautomaten, d. h. die Differenz zwischen der Volatilität von festem Geld und der Volatilität am Geldautomaten (unteres Diagramm). In den meisten Stichproben weisen Out-of-the-Money-Put-Optionen mit einer Geldmenge von 0,7 die höchste implizite Volatilität auf. Auf traditionellen (Aktien-)Märkten sind diese tief aus dem Geld liegenden Put-Optionen eine attraktive Versicherung gegen fallende Aktienkurse. Beispielsweise führt die ausgeprägte und nahezu linear verzerrte Form der impliziten Volatilitätskurve beim S&P 500 dazu, dass die Optionen mit der geringsten Geldwertigkeit nach einem Rückgang des Basiswerts am stärksten im Preis steigen. Im Gegensatz dazu zeigt Abbildung 3, dass die implizite Volatilitätskurve von Bitcoin vor dem Absturz am 12. März 2020 relativ symmetrisch war. ATM-Optionen haben mit rund 50 % die niedrigste Volatilität, während Out-of-the-Money-Puts und Out-of-the-Money-Calls ungefähr die gleiche Volatilität aufweisen, aber beide höher sind, wobei die Volatilität der Geldoptionen 0,7 und 1,3 beträgt rund 75 %. Allerdings war bei dem Absturz auch eine deutliche asymmetrische Tendenz zu beobachten: Aus dem Geld liegende Put-Optionen erzielen bei risikoscheuen Anlegern höhere Prämien für den Fall, dass die Kurse wieder stark fallen. Die implizite Volatilität von 30-tägigen, tief aus dem Geld liegenden Put-Optionen stieg plötzlich auf fast 200 %. Bei Bitcoin ist zum ersten Mal eine deutliche negative Schiefe zu beobachten, die Form ist jedoch im Vergleich zu den Schiefen, die typischerweise bei Aktienindexoptionen zu beobachten sind, noch immer viel flacher. Diese Asymmetrie bleibt bestehen, doch mit abnehmendem Niveau der impliziten Volatilität nimmt die Kurve der impliziten Volatilität wieder die Form eines Lächelns an.

Abbildung 3. Implizite Volatilität und ATM-Bias bei Bitcoin.

Die Abbildung zeigt die implizite Volatilitätskurve für Bitcoin-Optionen mit einer Laufzeit von 30 Tagen und einem Zeitraum vom 1. Januar 2020 bis 30. Juni 2022. Die Kurve wird unter Verwendung von Out-of-the-Money- und At-the-Money-Optionen berechnet, wobei die Ausübungspreise von einem Rückgang von 30 % bis zu einer Steigerung von 30 % des aktuellen Werts des Bitcoin-Index reichen.

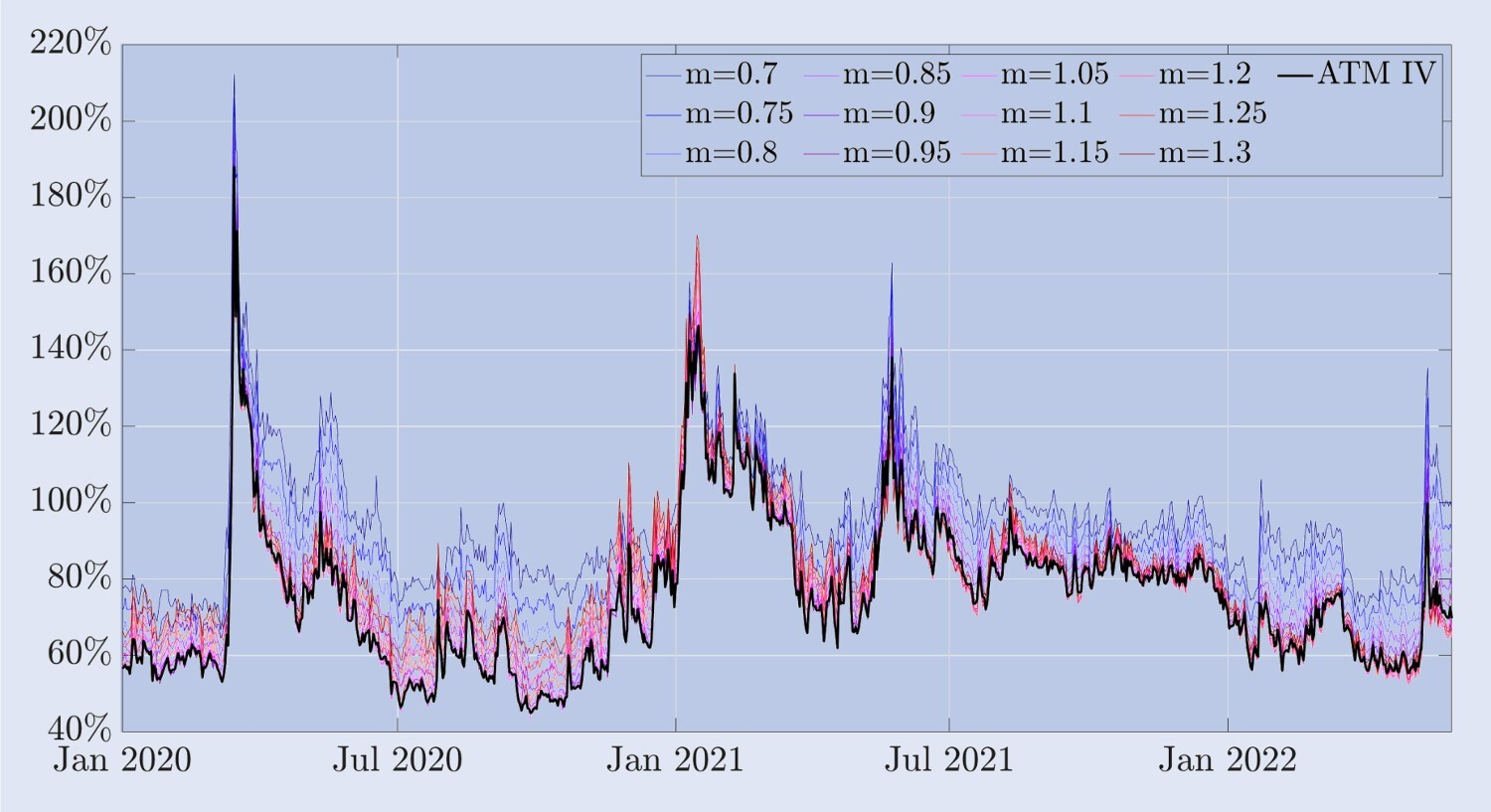
Basierend auf unseren Beispieldaten scheint die implizite Volatilität am Geld (ATM, at the Money) der niedrigste Punkt der Smile-Kurve zu sein und ist die meiste Zeit negativ verzerrt. Im Gegensatz zu Aktienindexoptionen weist die „Smiling Curve“ in Zeiten hoher Volatilität jedoch eine signifikante positive Schiefe auf. Beispielsweise nahm während des Bitcoin-Anstiegs im Juni 2021 die Steigung der Smile-Kurve zu und blieb mehrere Monate lang positiv verschief. Während die Korrelation zwischen Aktienindexpreisen und Volatilität fast immer groß und negativ ist, scheint die Korrelation zwischen Bitcoin-Preisen und seiner impliziten Volatilität von den Marktbedingungen abzuhängen. Von August 2019 bis November 2020 betrug die Korrelation zwischen dem Bitcoin-Preis und der impliziten Volatilität am Geldautomaten über 30 Tage etwa -0,42; in den nächsten fünf Monaten stieg die Korrelation auf 0,74; und im Jahr 2022 stieg die Korrelation auf 0,74. Von Juli bis November 2017 betrug die Korrelation zwischen Preis und Volatilität 0,08.

Einige Merkmale ähneln jedoch denen der impliziten Volatilität von Aktienindexoptionen: (i) Die Volatilität verschiedener Virtualitäten korreliert stark mit der At-the-Money-Volatilität derselben Laufzeit, wie in Abbildung 3 dargestellt; (ii) die Die implizite Volatilität von Bitcoin beträgt: Die Volatilitäts-Terminstruktur zeigt regelmäßige Schwankungen zwischen Reverse-Futures mit hoher Volatilität und Forward-Futures mit relativ ruhiger Volatilität. Abbildung 4 zeigt, dass die implizite Volatilität von Bitcoin während des größten Teils des inversen Futures-Zeitraums geringere Schwankungen und ähnliche Trends aufweist, ähnlich der Volatilitäts-Termstruktur von Aktienindizes.

Abbildung 4. Implizite Volatilitäts-Termstrukturkurve von Bitcoin.

Die implizite Volatilitätslaufzeitstruktur von Bitcoin-Optionen, einschließlich konstanter Verfallsdaten von 10, 20 und 30 Tagen, vom 1. Januar 2020 bis zum 31. Dezember 2021, berechnet basierend auf At-the-Money-Optionen. In relativ ruhigen Zeiten zeigt die Laufzeitstruktur positive Futures, während in Krisenzeiten (insbesondere im März 2020 und Juni 2021) das Gegenteil der Fall ist.

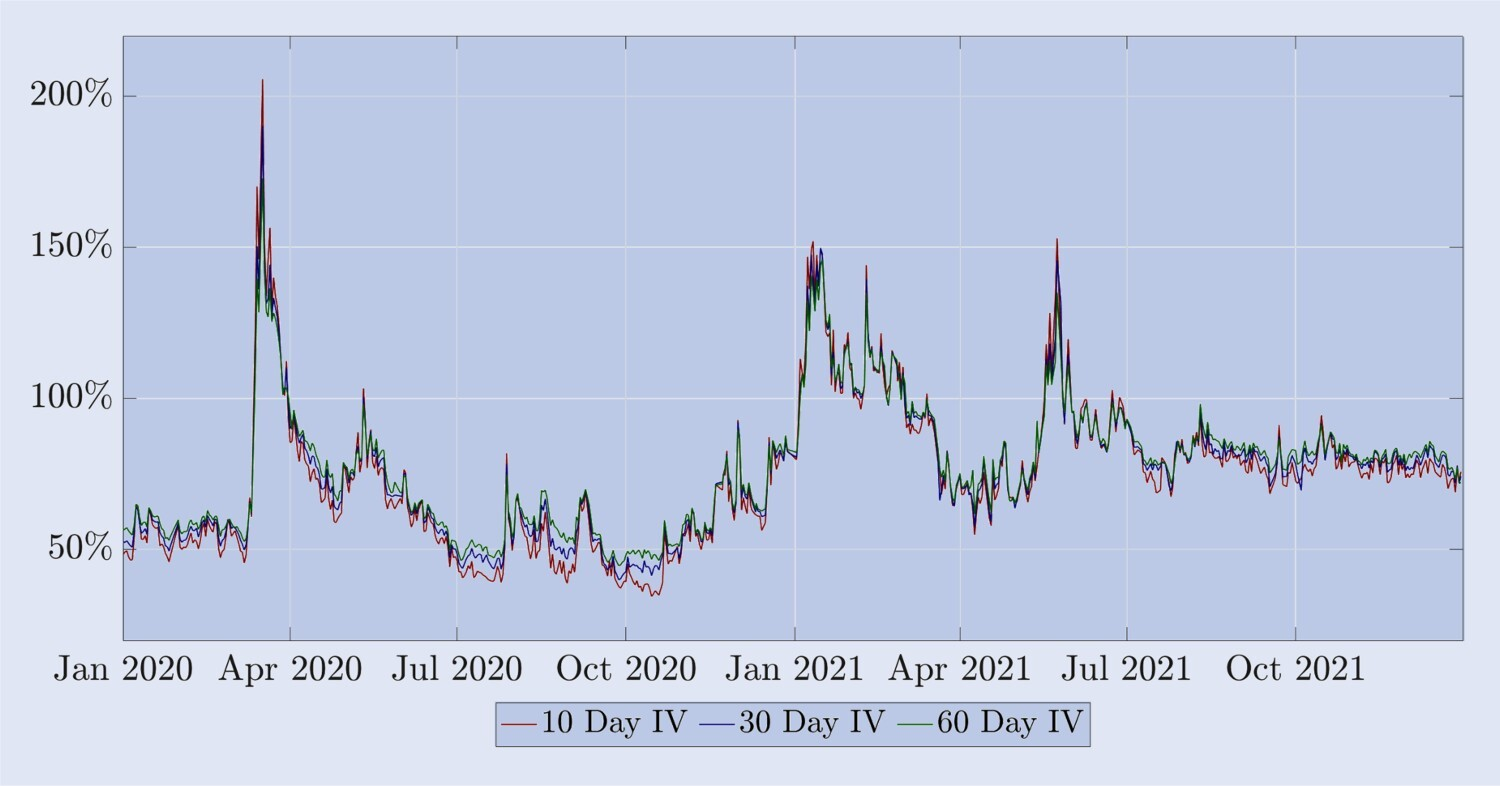
Wir leiten den Rest dieses Artikels mit den oben hervorgehobenen Eigenschaften von Bitcoin-Optionen und -Futures ein. Ein langfristiger Bitcoin-Inhaber könnte zum Schutz vor einem deutlichen Preiseinbruch eine Out-of-the-Money-Put-Option erwerben und eine entsprechende Absicherung der Spot-Position in Erwägung ziehen. Allerdings beteiligen sich Market Maker und andere professionelle Händler aktiv am dynamischen Delta-Hedging, da die Absicherung des Optionsrisikos für sie als Liquiditätsanbieter von entscheidender Bedeutung ist. Sie könnten BS Delta verwenden, um diese Absicherung durchzuführen, aber angesichts der Häufigkeit der Smile Curve Delta-Anpassung unter Aktienoptionshändlern wäre es interessant, die Wirksamkeit dieses Deltas für Bitcoin-Optionen zu untersuchen. Wir haben die Literatur überprüft, in der die Wirksamkeit des anhand der Smiling Curve angepassten Deltas zur Absicherung von Aktienindexoptionen erörtert wird, und gezeigt, dass BS Delta in vielen Fällen genauso wirksam ist wie jedes anhand der Smiling Curve angepasste Delta. Bisher wurde diese Frage jedoch nicht für Bitcoin-Optionen untersucht, und es ist klar – aus dem sehr unterschiedlichen Verhalten der impliziten Volatilitätskurve von Bitcoin, das wir gerade besprochen haben, und der Reihe neuer Absicherungsinstrumente, die für Bitcoin verfügbar sind – dass wir nicht einfach extrapolieren können Was über Aktienindexoptionen bekannt ist, um Rückschlüsse auf die Absicherung von Bitcoin-Optionen zu ziehen. Daher besteht der Zweck dieser Studie darin, verschiedene von Praktikern häufig verwendete, an die Smiling Curve angepasste Deltas vorzustellen und zu vergleichen, um ihre Wirksamkeit bei der Minimierung der Standardabweichung von Absicherungsfehlern bei Bitcoin-Optionen basierend auf der Auswahl unterschiedlicher Absicherungsinstrumente zu analysieren. Tatsächlich könnte diese Forschung sogar noch weiter auf die Börsenebene ausgedehnt werden, wo Optionen gehandelt und/oder abgesichert werden. Ist es beispielsweise besser, Binance- oder Deribit-Futures oder unbefristete Verträge zu verwenden, um an der Deribit-Börse notierte Optionen abzusichern? Wir diskutieren in dieser Studie jedoch nicht diese Detailebene des Bitcoin-Optionsabsicherungsproblems. Zumindest derzeit (zum Zeitpunkt des Schreibens) macht der Deribit-Optionsmarkt über 90 % des gesamten Bitcoin-Optionsvolumens aus, und persönliche Kommunikation mit Deribit-Options-Market-Makern zeigt, dass sie die Deribit-Futures-Plattform nur für Delta-Hedging-Aktivitäten verwenden.

4. Sicherungsverhältnis

In unserem Versuchsdesign schreiben wir eine Standard-Europäische Option auf Bitcoin-Index-Futures im Wert von einem Bitcoin und sichern sie ab, indem wir eine Long-Position in einer bestimmten Anzahl von Futures-Kontrakten eingehen. Mit T-verfallenden Futures können Händler eine Vereinbarung zum Kauf oder Verkauf einer bestimmten Menge Bitcoin zu einem zukünftigen Zeitpunkt T zu einem jetzt vereinbarten Bitcoin-USD-Wechselkurs treffen. Der Basiswert für Futures und Optionen ist der Deribit Bitcoin Index BTC, ein nicht handelbarer zusammengesetzter Index. Wir können die T-Verfallsoptionen jedoch auch mit einer unbefristeten Vertragsposition anstelle eines T-Verfalls-Futures-Kontrakts absichern. Wir können die Laufzeit t in unserer Notation weglassen, ohne Verwirrung zu stiften, und bezeichnen den Preis zum Zeitpunkt t einer inversen Option mit Ausübungspreis K und Verfallsdatum T als f(K,T|F,σ), wobei F Der ewige Preis oder Futures-Preis mit Ablauf bei T zum Zeitpunkt t, σ:=σt(K,T|F), stellt die implizite Volatilität der Option dar, die auch der Volatilität zum Zeitpunkt t entspricht. Durch die Einbeziehung der Beziehung zwischen Volatilität und dem zugrunde liegenden Vermögenswert in unseren Absicherungsrahmen möchten wir ein genaueres Delta als das BS-Delta erreichen, nämlich das Smile-bereinigte Delta δadj basierend auf der Kettenregel.

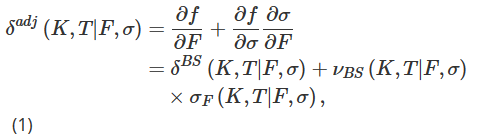
Dabei ist δBS das Standard-BS-Delta, νBS die Volatilitätssensitivität des BS-Optionspreises (Vega) und σF = ∂σ/∂F die Volatilitätssensitivität gegenüber dem Preis, d. h. die Änderung der impliziten Volatilität gegenüber Änderungen des Basiswerts . . Obwohl BS Delta und Vega über geschlossene Formeln verfügen und leicht zu berechnen sind, ist die Quantifizierung von σF relativ schwierig und es gibt viele verschiedene Methoden.

Die erste von uns besprochene Anpassung des BS-Deltas hat ihre Wurzeln in unterschiedlichen Möglichkeiten der Parametrisierung der lokalen Volatilität, je nach aktuellem Marktzustand oder „Marktregime“. Das Konzept der lokalen Volatilität wurde in zahlreichen wissenschaftlichen Veröffentlichungen entwickelt, angefangen mit den klassischen Arbeiten von Dupire (1994) und Derman et al. (1996). Von besonderem Interesse ist hier das von Derman (1999) im Zusammenhang mit der Absicherung von Aktienindexoptionen vertretene „Sticky-Modell“, das unterschiedliche lokale Volatilitätsparametrisierungen an den Knotenpunkten eines binären Baums anwendet, der die Entwicklung des Preises des zugrunde liegenden Vermögenswerts modelliert. Derman et al. (1996) schlugen vor, σF als Steigung der impliziten Volatilität in Bezug auf den Ausübungspreis zu approximieren: Anmerkung 13

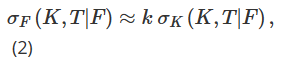
Unter diesen stellt σK=∂σ/∂K die Ableitung der Volatilität in Bezug auf den Ausübungspreis dar, und k sollte vom aktuellen Marktmechanismus abhängen. Tatsächlich führte Derman (1999) drei verschiedene „Stickiness-Modelle“ ein, um das lokale Volatilitätsverhalten unter verschiedenen Marktregimen darzustellen. Das Sticky Strike Modell (SS) beschreibt eine trendmäßige Marktsituation und geht davon aus, dass die Volatilität unabhängig von zukünftigen Preisbewegungen des Basiswerts ist und, wie die BS-Annahme, konstant und für jede Option gleich ist. In diesem Mechanismus ist Delta gleich BS-Delta. Anmerkung 14: Das Sticky Money (SM)-Modell (manchmal auch Sticky Delta genannt) berücksichtigt einen bereichsgebundenen Markt. Bei diesem Mechanismus hängt die Volatilität einer Option nur von ihrer Geldwertigkeit (oder gleichwertig ihrem Delta) ab. Daher ist die lokale Volatilität an jedem Knoten des Baums gleich, aber jede Option hat einen anderen Baum mit unterschiedlicher lokaler Volatilität, abhängig von der Geldwertigkeit der Option. Wenn sich der Preis des Basiswerts ändert, ändert sich die Geldwertigkeit der Option und wir müssen zu einem anderen Baum wechseln, um die Option zu bewerten. Schließlich erfasst das Sticky Tree-Modell (ST) das lokale Volatilitätsverhalten während schneller Marktrückgänge, d. h. es beschreibt eine „Smiling Curve“-Anpassung, wenn eine starke negative Korrelation zwischen der Volatilität und dem Preis des zugrunde liegenden Vermögenswerts besteht. Der Name dieses Hidden-Tree-Modells leitet sich vom lokalen Volatilitätsmodell ab, das von Derman und Kani (1994) vorgeschlagen wurde. Ebenso ist die lokale Volatilität eine deterministische Funktion, sie kann jedoch an jedem Knoten im Baum unterschiedlich sein, und für die Preisgestaltung aller Optionen wird derselbe Baum verwendet. Bei diesen drei verschiedenen Arten der lokalen Volatilitätsparametrisierung ist der Wert von k in Formel (2) je nach Marktmechanismus unterschiedlich, wie unten gezeigt:

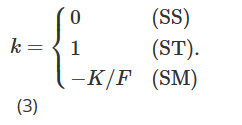
Crépey (2004) und Alexander et al. (2012) erweiterten beide die Näherung (2), um die Zustandsabhängigkeit von k einzubeziehen. Beachten Sie auch, dass durch Kombination der Gleichungen (1) und (2) von Alexander et al. (2012) mit Gleichung (3) von Alexander und Nogueira (2007b) und Durchführung einiger algebraischer Manipulationen festgestellt werden kann, dass die Smile-Kurve von Bates ( 2005) ist implizit. Das , skaleninvariante Delta (verallgemeinert in Alexander und Nogueira (2007a)) ist identisch mit der Sticky-Money-(SM)-Approximation.

Angesichts der hohen Volatilität von Bitcoin kann die Bandbreite der verfügbaren Ausübungspreise im Laufe der Zeit erheblich schwanken. Um einen Rahmen für die Untersuchung von Optionen mit denselben Eigenschaften über einen längeren Zeitraum bereitzustellen, wenden wir uns daher von Ausübungspreisen den In-the-Money-Indikatoren zu. Wir definieren die Geldlichkeit m als m=K/F und verwenden nun θ(m,T|F)=σ(mK,T|F), um die implizite Volatilität darzustellen. Wenn wir die partiellen Ableitungen von θ(m,T|F) bezüglich F und m als θF(m,T|F) bzw. θm(m,T|F) bezeichnen, können wir das angepasste Delta (7) wie folgt umschreiben:

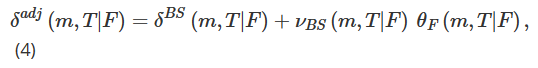
Wir verwenden die von Derman (1999) vorgeschlagene Hypothese der lokalen Volatilität, um die Volatilitäts-Preis-Sensitivität θF zu schätzen. Die zur Simulation der Optionspreisentwicklung verwendete Baumstruktur unterscheidet sich je nach den drei möglichen Marktmodellen: Stable Trend Market (SS), Range Market (SM) und Jump Crash Market (ST). Daher sollte der Wert von κ in (5) bei der Umwandlung von Dermans (1999) Sticky Delta in eine monetäre Messung je nach Marktmodell unterschiedlich sein.

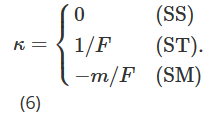
Wie zuvor ist das von Bates (2005) und Alexander und Nogueira (2007a) vorgeschlagene modellfreie, Smile-implizite, skaleninvariante Delta identisch mit dem Sticky-Money-Maß (SM) Delta von Derman und Kani (1994).

Als nächstes betrachten wir die minimale Varianz (MV) Delta δmv, d. h. das Delta, das die momentane Varianz des Delta-Hedge-Portfolios minimiert. Hier folgen wir einer von Bakshi et al. (1997) eingeführten Näherung, die die lokale Varianz minimiert. Lee (2001) zeigt, dass diese Anpassung des MV-Hedge-Verhältnisses dieselbe Größenordnung hat wie das (SM) Smile Implied Delta, jedoch mit entgegengesetztem Vorzeichen, d. h.:

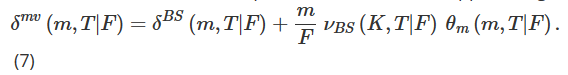
Wie in Kapitel 4 von Alexander (2008) und auch in anderen Texten zur impliziten Volatilität ausführlich erläutert, erzeugt das implizite Delta des Smiles eine kontraintuitive „Floating Smile“-Dynamik, die auch bedeutet, dass bei Volatilität Wenn die Kurs-Preis-Korrelation groß ist und negativ (d. h. es liegt eine erhebliche negative Schiefe vor), ist die durch die SM-Anpassung erzielte Absicherungsleistung erheblich schlechter als die BS-Delta. Da die MV-Anpassung ein entgegengesetztes Vorzeichen zur SM-Anpassung hat, sollte das MV-Delta dem BS-Delta vorgezogen werden, wenn es um die Absicherung von Aktienindexoptionen und allen Optionen mit einer impliziten Volatilitätskurve mit einer signifikanten negativen Steigung geht.

Unser endgültiges Lächelkurvenanpassungs-Delta, bezeichnet mit δhw, wird von Hull und White (2017) vorgeschlagen. Es wird durch empirische Schätzung der quadratischen Beziehung zwischen dem absoluten Wert des täglichen PnL ΔP des BS-Delta-Hedge-Portfolios und dem BS-Delta abgeleitet. Das heißt:

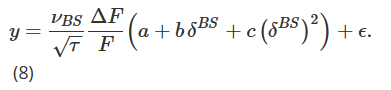
wobei ΔF der tägliche PnL der Futures ist. Nach dem Erhalt der Parameterschätzungen (aˆ, bˆ, cˆ) unter Verwendung historischer Daten wird das Hull- und White-Delta (HW) wie folgt berechnet:

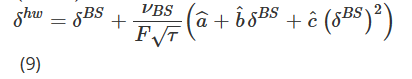
wobei δBS und νBS das klassische BS Delta und Vega darstellen. Der aktuelle Basispreis wird mit F bezeichnet, seine Änderung mit ΔF und τ stellt den Verfallszeitpunkt der Option dar. Die Autoren berechnen die Schätzungen (aˆ, bˆ, cˆ) anhand eines 36-monatigen gleitenden Fensters und analysieren dann die Performance des HW-Delta-Hedges, um die Standardabweichung des täglichen Hedge-Fehlers für einen 11-Jahres-Zeitraum ab Januar 2014 zu minimieren. S&P 500 und andere Aktienindexoptionen. Sie fanden heraus, dass die Leistung durch den Einsatz von HW Delta um bis zu 26 % gesteigert werden konnte. Andere Schlussfolgerungen basieren ausschließlich auf Aktienindexoptionen und argumentieren, dass HW Delta Put-Optionen bei Calls und In-the-Money-Optionen bei Out-of-the-Money-Optionen übertrifft. Darüber hinaus behaupten sie, dass HW Delta bei der Absicherung von Aktienindexoptionen viele andere Deltas übertrifft, die aus verschiedenen stochastischen Volatilitäts- und lokalen Volatilitätsmodellen abgeleitet werden.

In diesem Abschnitt werden eine Reihe einfacher Anpassungen an BS Delta behandelt, die in früheren Untersuchungen zur Absicherung von Aktienindexoptionen und anderen traditionellen Anlageklassen ihre Wirksamkeit unter Beweis gestellt haben. Die Frage ist nun, ob sie auch im Bitcoin-Optionsmarkt eine bessere Performance als einfaches BS-Delta-Hedging erzielen können. Der Bitcoin-Optionsmarkt ist weniger ausgereift als herkömmliche Optionsmärkte. Seine Volatilität und sein richtungsweisender Kaufdruck sind stärker ausgeprägt. Market Maker gleichen ihre Lagerbestände auf der Grundlage der durch diesen Druck hervorgerufenen Informationen neu aus. Wir fassen die in dieser Studie berücksichtigten BS-bereinigten Delta-Hedge-Verhältnisse in der folgenden einzigen Formel zusammen:

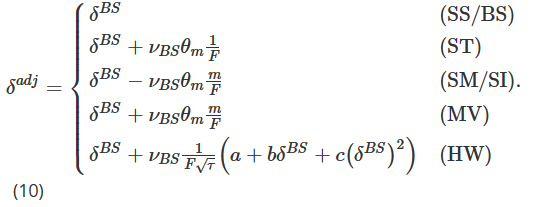
Wir erläutern die oben genannten Inhalte wie folgt:

1. Wenn m=1, also bei einer At-the-Money-Option, ist die MV-Anpassung gleich der ST-Anpassung; andernfalls, wenn m>1, also bei einer Out-of-the-Money-Call-Option, die Größe der MV-Anpassung ist größer als die ST-Anpassung; wenn m, d. h. bei einer Out-of-the-Money-Put-Option, ist die Größe der MV-Anpassung kleiner als die ST-Anpassung;

2. Die MV-Anpassung ist immer gleich groß und entgegengesetzt zur SM-Anpassung, und das SM-Delta ist auch das modellfreie skalierungsinvariante (SI) Delta von Alexander und Nogueira (2007a), d.h. das Delta jeder Art von stochastischer Volatilitätssprungprozess bei Bitcoin-Optionspreisen;

3. Die Vorzeichen der ST-, SM- und MV-Anpassungen hängen von der Steigung der impliziten Volatilitätskurve θm ab. Bei einer negativen Steigung sind MV und ST Delta kleiner als BS/SS Delta, während SM/SI Delta größer als BS/SS Delta ist. Bei einer positiven Steigung sind MV und ST Delta größer als BS/SS Delta, während SM/SI Delta kleiner als BS/SS Delta ist.

5. Daten

Wir haben eine einzigartige Datenbank erstellt, indem wir über einen Zeitraum von mehreren Jahren mithilfe der Börsen-API stündliche Schnappschüsse der Deribit-Optionsmarktdaten erstellt haben. Diese Daten enthalten die Orderbuchinformationen der Ebene 1 für alle Optionen, Futures und unbefristeten Kontrakte. In diesem Artikel verwenden wir ausschließlich Daten mit achtstündigen und täglichen Frequenzen, die einen Zweijahreszeitraum vom 1. Januar 2020 bis zum 1. Januar 2022 abdecken.

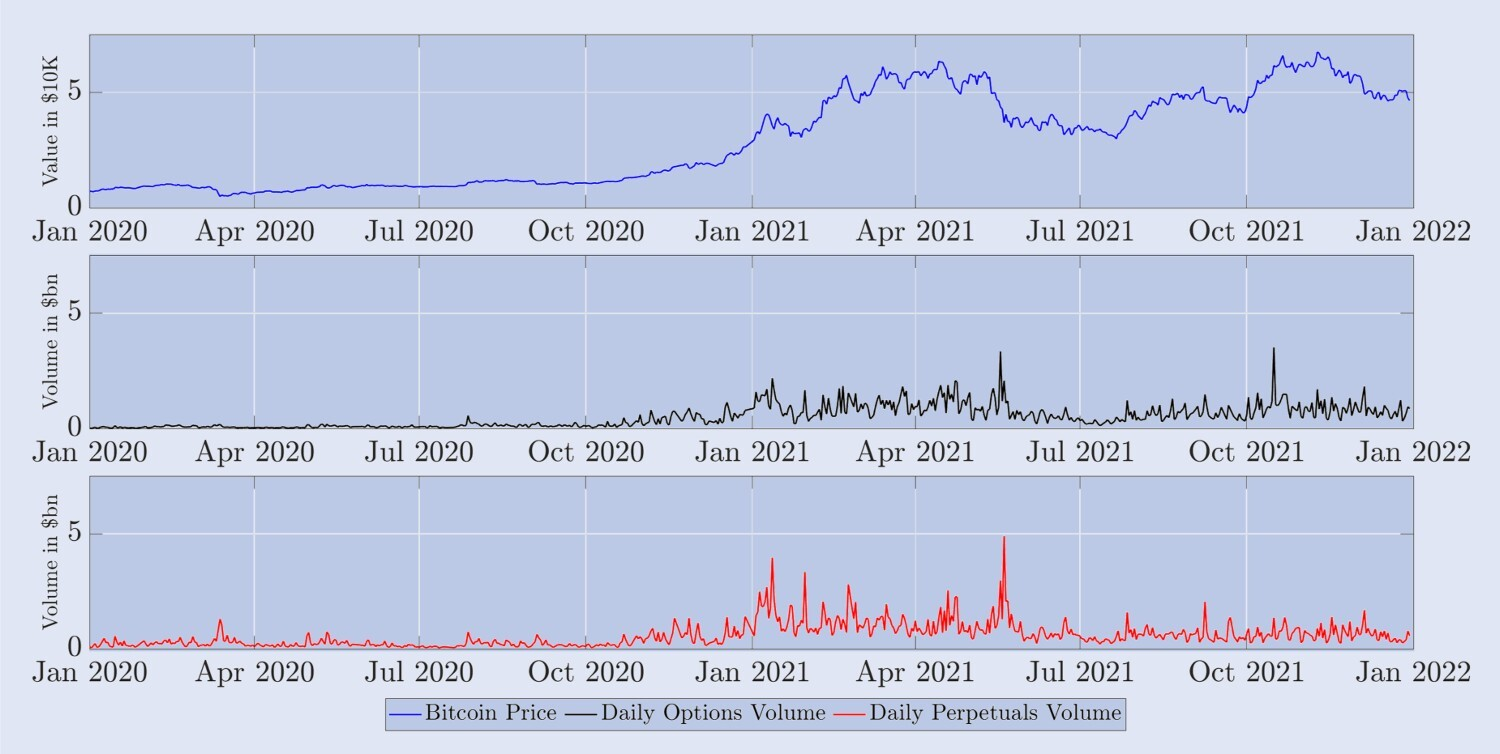
Abbildung 5 zeigt den täglichen Abrechnungspreis des BTC-Index (d. h. den Preis um 00:00 UTC) und das Gesamtvolumen aller auf Deribit in den letzten 24 Stunden gehandelten Optionen und unbefristeten Kontrakte (in Nominalbeträgen, in Milliarden USD). . Terminkontrakte sind hier nicht berücksichtigt, da ihr Handelsvolumen viel geringer ist als bei unbefristeten Kontrakten und Optionen, wie Abbildung 1 zeigt. Im Laufe des Jahres 2020 stieg der BTC-Index relativ langsam von einem Niveau um 7.000 \( bis zum ersten großen Bullenlauf, der im November 2020 begann und bei dem der Indexwert Ende 2020 fast 28.000 \) erreichte. Im Jahr 2021 verdoppelte sich der BTC-Index von Januar (rund 28.000 \() bis Mitte April 2021 (rund 59.000 \)) und fiel danach um fast 50 %, bis er Mitte Juli wieder auf 30.000 \( fiel. Am 8. November 2021 erreichte es ein Allzeithoch von rund 69.000 \). Der mittlere Bereich von Abbildung 5 zeigt, dass das gesamte 24-Stunden-Handelsvolumen aller Optionen auf Deribit im Jahr 2020 relativ niedrig war und kaum 500 Millionen US-Dollar überstieg. Im Jahr 2021 gab es jedoch deutlich volatile oder trendige Märkte, wobei die täglichen Optionsvolumina häufig bei 3 Milliarden US-Dollar lagen. Auch die Zahl der gehandelten unterschiedlichen Optionskontrakte hat sich fast verdoppelt, von 4,3 Millionen im Januar 2021 auf 6,2 Millionen zum Jahresende. Die folgende Grafik zeigt das tägliche Handelsvolumen unbefristeter Kontrakte, bei denen im Jahr 2021, insbesondere in der ersten Jahreshälfte, eine höhere Handelsaktivität zu verzeichnen war. Interessanterweise war das Handelswachstum bei unbefristeten Kontrakten im zweiten Halbjahr 2021 schwächer als bei Optionen. Letzteres ist wahrscheinlich auf die Einführung einer Reihe neuer Kontrakte Ende 2020 und Anfang 2021 zurückzuführen, die von Händlern nach und nach zur Gamma- und Vega-Absicherung übernommen wurden. Dies dürfte den Druck auf das äußerst aktive dynamische Delta-Hedging im zweiten Halbjahr 2021 verringert haben. Tatsächlich sind, wie Abbildung 1 zeigt, auch die Handelsvolumina für Terminkontrakte in den letzten sechs Monaten des Jahres 2021 zurückgegangen, sogar noch stärker als die für unbefristete Kontrakte. Ungeachtet dessen veranlasste uns die Feststellung, dass die Handelsmuster in den Jahren 2020 und 2021 so unterschiedlich waren, dazu, die Stichprobe in zwei Einjahreszeiträume aufzuteilen.

Abbildung 5. Entwicklung des BTC-Index und des täglichen Handelsvolumens von Derivaten.

Das obige Diagramm zeigt den BTC-Indexpreis täglich um 00:00 UTC für einen zweijährigen Beispielzeitraum, beginnend am 1. Januar 2020 (oben, blaues Diagramm); das entsprechende 24-Stunden-Gesamtvolumen aller Optionen auf Deribit (Mitte, schwarz Diagramm); und das tägliche Handelsvolumen unbefristeter Kontrakte (unten, rotes Diagramm). Der Wert des BTC-Index wird in Einheiten von 10.000 US-Dollar angegeben und das Handelsvolumen beläuft sich auf Milliarden von Dollar.

Alexander et al. (2022b) dokumentieren viele Unterschiede zwischen den Bitcoin- und S&P 500-Optionsmärkten. Einer der Hauptunterschiede besteht im Anteil der gehandelten Short-, Medium- und Long-Optionen. Einmonatige Optionen auf den S&P 500 sind relativ kurzfristig, da der Großteil des Handels zwischen der Laufzeit von einem und drei Monaten stattfindet. Eine Bitcoin-Option mit einem Verfallsdatum von einem Monat fällt jedoch in die Kategorie der längerfristigen Optionen. Um dies ins rechte Licht zu rücken, zeigt Abbildung 6 den Anteil der auf Deribit gehandelten Kontrakte nach Ablaufzeitpunkt. Die durchgezogene Linie auf der rechten Skala stellt die Anzahl der Trades für alle auslaufenden Kontrakte dar. Der Übersichtlichkeit halber stellen wir diese Daten als wöchentliche Durchschnittswerte über ein gleitendes Fenster dar. Das saisonale Muster im Anteil der kurzfristigen Optionen (bis zu zwei Wochen) ist ein Ergebnis der Emissionsplanungspolitik, die besagt, dass, sofern in dieser Woche (oder in zwei Wochen) keine standardmäßige monatliche oder vierteljährliche Option ausläuft, eine Option Es werden Optionen mit einer (bzw. zwei) Verfallszeit von einer Woche (bzw. zwei Wochen) ausgegeben. Auf der linken Skala stellen wir den Anteil der kurzfristigen (bis zwei Wochen), mittelfristigen (zwischen zwei Wochen und einem Monat) und langfristigen (mehr als ein Monat) Laufzeiten dar. Dazu aggregieren wir alle täglich gehandelten Kontrakte innerhalb jeder Verfallskategorie und stellen sie als Prozentsatz aller gehandelten Kontrakte dar, wobei wir der Übersichtlichkeit halber wiederum einen gleitenden Wochendurchschnitt verwenden. Abgesehen von diesem saisonalen Muster entfielen im gesamten Zweijahreszeitraum nur etwa 15 bis 20 Prozent des Handels auf Optionen mit Verfallsdaten von mehr als einem Monat. Trotz der steigenden Zahl gehandelter Kontrakte in unserer Stichprobe ist der Anteil der Kont