Letzte Woche haben wir vorgestelltVaR-RisikomanagementBeim Risiko eines Portfolios geht es nicht um das Risiko der einzelnen Vermögenswerte, sondern um deren Preiskorrelation. Nehmen wir als Beispiel zwei Vermögenswerte: Wenn ihre positive Korrelation sehr stark ist, das heißt, sie gemeinsam steigen und fallen, dann wird die Diversifizierung langfristiger Investitionen das Risiko nicht verringern. Wenn die negative Korrelation sehr stark ist, kann die Diversifizierung das Risiko deutlich verringern. Die natürliche Frage ist: Wie können Sie bei der Investition in ein Portfolio bei einem bestimmten Risikoniveau die Rendite maximieren? Hier kommt die Markowitz-Theorie ins Spiel, die ich heute vorstellen werde.

Die Moderne Portfoliotheorie (MPT), die 1952 von Harry Markowitz vorgeschlagen wurde, ist ein mathematischer Rahmen für die Portfolioauswahl, der darauf abzielt, durch die Auswahl verschiedener risikoreicher Anlagekombinationen die erwarteten Erträge zu maximieren und gleichzeitig die Gewinne zu kontrollieren. Der Kerngedanke besteht darin, dass sich die Preise von Vermögenswerten nicht perfekt synchron bewegen (d. h., es besteht eine unvollständige Korrelation zwischen den Vermögenswerten) und dass das Gesamtanlagerisiko durch eine Diversifizierung der Vermögensallokation verringert werden kann.

Schlüsselkonzepte der Markowitz-Theorie

1. Erwartete Rendite: Dies ist die Rendite, die ein Anleger durch das Halten eines Vermögenswerts oder Portfolios erwarten kann. Sie wird normalerweise auf Grundlage historischer Renditedaten vorhergesagt.

\(E(R_p) = \sum_{i=1}^{n} w_i E(R_i)\)

Dabei ist \(E(R_p)\) die erwartete Rendite des Portfolios, \(wi\) das Gewicht des i-ten Vermögenswerts im Portfolio und \(E(R_i)\) die erwartete Rendite des \( i\)ter Vermögenswert. .

1. Risiko (Volatilität oder Standardabweichung): Wird verwendet, um die Unsicherheit der Anlagerendite oder die Volatilität einer Anlage zu messen.

\(\sigma_p = \sqrt{\sum_{i=1}^{n} \sum_{j=1}^{n} w_i w_j \sigma_{ij}}\)

Dabei ist \(\sigma_p\) das Gesamtrisiko des Portfolios und \(\sigma_{ij}\) die Kovarianz zwischen Vermögenswert \(i\) und Vermögenswert \(j\), die die Beziehung zwischen den Preisänderungen der beiden Vermögenswerte misst.

1. Kovarianz: Misst die Korrelation zwischen den Preisbewegungen zweier Vermögenswerte.

\(\sigma_{ij} = \rho_{ij} \sigma_i \sigma_j\)

Wobei \(\rho_{ij}\) der Korrelationskoeffizient zwischen Vermögenswert \(i\) und Vermögenswert \(j\) ist und \(\sigma_i\) und \(\sigma_j\) die Standardabweichungen von Vermögenswert \(i\) bzw. Vermögenswert \(j\) sind.

1. Effiziente Grenze: Im Risiko-Rendite-Koordinatensystem ist die Effizienzgrenze die Menge der Portfolios, die bei einem bestimmten Risikoniveau die maximal erwartete Rendite bieten können.

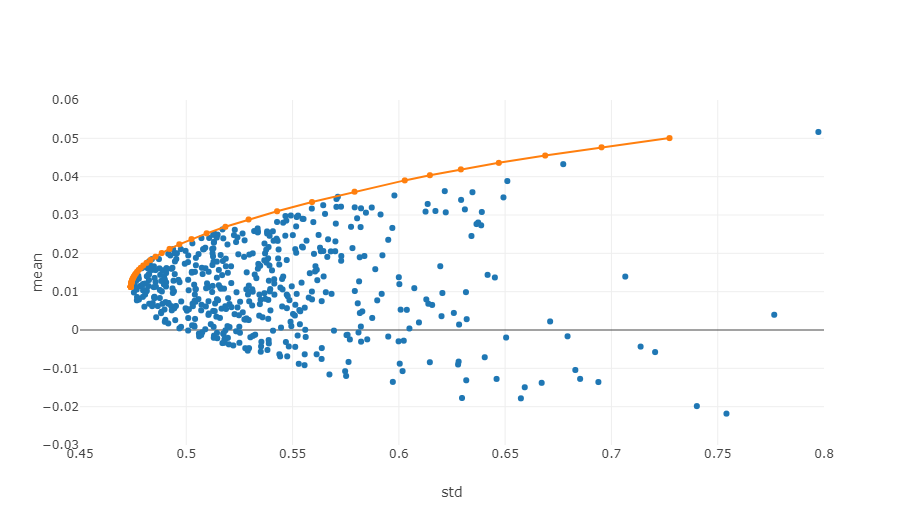
Das obige Bild ist ein schematisches Diagramm der effektiven Grenze. Jeder Punkt stellt ein Anlageportfolio mit unterschiedlichen Gewichten dar. Die horizontale Achse ist die Volatilität, d. h. das Risikoniveau, und die vertikale Achse ist die Rendite. Natürlich konzentrieren wir uns auf den oberen Rand der Grafik, der bei gleichem Risikoniveau die höchste Rendite erzielt.

Beim quantitativen Handel und Portfoliomanagement erfordert die Anwendung dieser Prinzipien eine statistische Analyse historischer Daten und die Verwendung mathematischer Modelle zur Schätzung der erwarteten Renditen, Standardabweichungen und Kovarianzen verschiedener Vermögenswerte. Anschließend werden Optimierungstechniken angewendet, um die beste Vermögensgewichtskonfiguration zu finden. Dieser Prozess erfordert in der Regel komplexe mathematische Berechnungen und einen hohen Computeraufwand, weshalb die quantitative Analyse in der modernen Finanzwelt eine so große Bedeutung erlangt hat. Im Folgenden wird die Optimierung anhand eines konkreten Python-Beispiels veranschaulicht.

Python-Codebeispiel zum Finden der optimalen Kombination mithilfe der Simulationsmethode

Die Berechnung des optimalen Markowitz-Portfolios ist ein mehrstufiger Prozess, der mehrere wichtige Schritte wie Datenaufbereitung, Portfoliosimulation und Indikatorberechnung umfasst. Referenz: https://plotly.com/python/v3/ipython-notebooks/markowitz-portfolio-optimization/

1. Marktdaten abrufen：

   • passierenget_dataFunktion zum Abrufen der historischen Preisdaten der ausgewählten digitalen Währung. Dabei handelt es sich um die für die Berechnung der Rendite und des Risikos erforderlichen Daten, die zur Zusammenstellung von Portfolios und zur Berechnung der Sharpe-Ratio verwendet werden.

2. Berechnung von Rendite und Risiko：

   • verwendencalculate_returns_riskDie Funktion berechnet die annualisierte Rendite und das annualisierte Risiko (Standardabweichung) für jede digitale Währung. Dadurch soll die historische Performance jedes Vermögenswerts quantifiziert werden, um ihn in einem optimalen Portfolio zu verwenden.

3. Berechnen Sie das optimale Markowitz-Portfolio：

   • verwendencalculate_optimal_portfolioFunktion zur Simulation mehrerer Portfolios. Bei jeder Simulation werden die Vermögensgewichte nach dem Zufallsprinzip generiert und die erwartete Rendite und das Risiko des Portfolios werden dann auf Grundlage dieser Gewichte berechnet.
   • Durch die zufällige Generierung von Kombinationen mit unterschiedlichen Gewichtungen können mehrere mögliche Portfolios untersucht werden, um die beste Kombination zu finden. Dies ist eine der Kernideen der Portfoliotheorie von Markowitz.

Das Ziel des gesamten Prozesses besteht darin, das Portfolio zu finden, das bei einem gegebenen Risikoniveau die beste erwartete Rendite bietet. Durch die Simulation mehrerer möglicher Kombinationen können Anleger die Leistung verschiedener Konfigurationen besser verstehen und die Kombination auswählen, die ihren Anlagezielen und ihrer Risikobereitschaft am besten entspricht. Dieser Ansatz hilft, Anlageentscheidungen zu optimieren und Investitionen effizienter zu gestalten.

import numpy as np
import pandas as pd
import requests
import matplotlib.pyplot as plt

# 获取行情数据
def get_data(symbols):
    data = []
    for symbol in symbols:
        url = 'https://api.binance.com/api/v3/klines?symbol=%s&interval=%s&limit=1000'%(symbol,'1d')
        res = requests.get(url)
        data.append([float(line[4]) for line in res.json()])
    return data

def calculate_returns_risk(data):
    returns = []
    risks = []

    for d in data:
        daily_returns = np.diff(d) / d[:-1]
        annualized_return = np.mean(daily_returns) * 365
        annualized_volatility = np.std(daily_returns) * np.sqrt(365)

        returns.append(annualized_return)
        risks.append(annualized_volatility)

    return np.array(returns), np.array(risks)

# 计算马科维茨最优组合
def calculate_optimal_portfolio(returns, risks):
    n_assets = len(returns)
    num_portfolios = 3000

    results = np.zeros((4, num_portfolios), dtype=object) 


    for i in range(num_portfolios):
        weights = np.random.random(n_assets)
        weights /= np.sum(weights)

        portfolio_return = np.sum(returns * weights)
        portfolio_risk = np.sqrt(np.dot(weights.T, np.dot(np.cov(returns, rowvar=False), weights)))

        results[0, i] = portfolio_return
        results[1, i] = portfolio_risk
        results[2, i] = portfolio_return / portfolio_risk
        results[3, i] = list(weights) # 将权重转换为列表

    return results

symbols = ['BTCUSDT','ETHUSDT', 'BNBUSDT','LINKUSDT','BCHUSDT','LTCUSDT']
data = get_data(symbols)

returns, risks = calculate_returns_risk(data)
optimal_portfolios = calculate_optimal_portfolio(returns, risks)

max_sharpe_idx = np.argmax(optimal_portfolios[2])
optimal_return = optimal_portfolios[0, max_sharpe_idx]
optimal_risk = optimal_portfolios[1, max_sharpe_idx]
optimal_weights = optimal_portfolios[3, max_sharpe_idx]

# 输出结果
print("最优组合:")
for i in range(len(symbols)):
    print(f"{symbols[i]}权重: {optimal_weights[i]:.4f}")

print(f"预期收益率: {optimal_return:.4f}")
print(f"预期风险(标准差): {optimal_risk:.4f}")
print(f"夏普比率: {optimal_return / optimal_risk:.4f}")

# 可视化投资组合
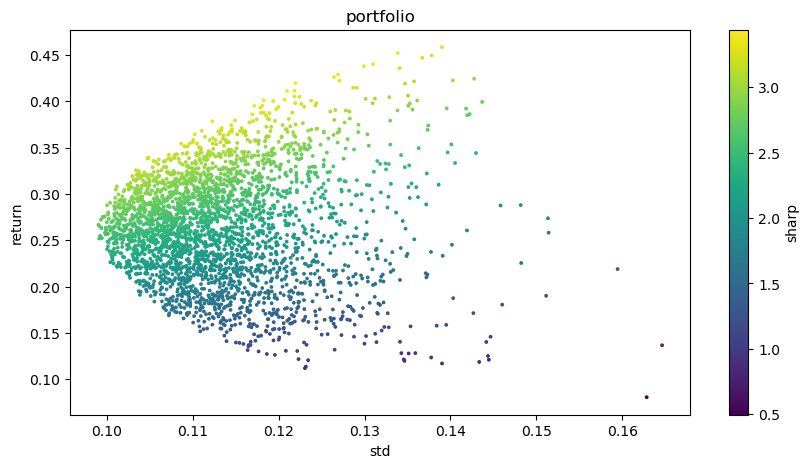
plt.figure(figsize=(10, 5))
plt.scatter(optimal_portfolios[1], optimal_portfolios[0], c=optimal_portfolios[2], marker='o', s=3)
plt.title('portfolio')
plt.xlabel('std')
plt.ylabel('return')
plt.colorbar(label='sharp')
plt.show()

Endgültige Ausgabe: Beste Kombination: BTCUSDT-Gewicht: 0,0721 ETHUSDT-Gewicht: 0,2704 BNUSDT-Gewicht: 0,3646 LINKUSDT-Gewicht: 0,1892 BCHUSDT-Gewicht: 0,0829 LTCUSDT-Gewicht: 0,0209 Erwartete Rendite: 0,4195 Erwartetes Risiko (Standardabweichung): 0,1219 Sharpe-Ratio: 3,4403