Die Bayessche Statistik ist eine leistungsfähige Disziplin der Mathematik mit vielfältigen Anwendungsmöglichkeiten in vielen Bereichen, unter anderem in der Finanzwelt, der medizinischen Forschung und der Informationstechnologie. Dadurch können wir frühere Überzeugungen mit Beweisen kombinieren, um zu neuen späteren Überzeugungen zu gelangen und so fundiertere Entscheidungen zu treffen.

In diesem Artikel stellen wir kurz einige der wichtigsten Mathematiker vor, die dieses Fachgebiet begründet haben.

Vor Bayes Um die Bayessche Statistik besser zu verstehen, müssen wir ins 18. Jahrhundert zurückgehen und uns auf den Mathematiker De Moivre und sein Werk „Das Prinzip des Zufalls“ beziehen.[1]。

In seiner Abhandlung ging De Moivre auf viele Probleme seiner Zeit im Zusammenhang mit Wahrscheinlichkeit und Glücksspiel ein. Wie Sie wahrscheinlich wissen, führte seine Lösung für eines dieser Probleme zur Entstehung der Normalverteilung, aber das ist eine andere Geschichte.

In seinem Artikel gibt es eine einfache Frage:

„Die Wahrscheinlichkeit, beim dreimaligen Werfen einer fairen Münze hintereinander dreimal Kopf zu erhalten.“

Beim Lesen der im „Prinzip des Zufalls“ beschriebenen Probleme werden Sie möglicherweise feststellen, dass die meisten von ihnen mit einer Hypothese beginnen, auf deren Grundlage die Wahrscheinlichkeit eines bestimmten Ereignisses berechnet wird. Im obigen Problem wird beispielsweise angenommen, dass die Münze fair ist und die Wahrscheinlichkeit, beim Münzwurf Kopf zu erhalten, daher 0,5 beträgt.

Mathematisch ausgedrückt wird dies heute so:

𝑃(𝑋|𝜃)

Was aber, wenn wir nicht wissen, ob die Münze fair ist? Wenn wir es nicht wissen𝜃Wolltuch?

Thomas Bayes und Richard Price

Fast fünfzig Jahre später, im Jahr 1763, erschien ein Aufsatz mit dem Titel „Ein Essay über das Prinzip des Zufalls“.[2] Veröffentlicht in den Philosophical Transactions der Royal Society of London.

Auf den ersten Seiten des Dokuments befindet sich ein Text des Mathematikers Richard Price, der den Inhalt einer Abhandlung seines Freundes Thomas Bayes zusammenfasst, die dieser einige Jahre vor seinem Tod verfasst hatte. In der Einleitung erklärt Price die Bedeutung einiger Entdeckungen von Thomas Bayes, die in De Moivres „Principles of Chance“ nicht behandelt werden.

Tatsächlich bezog er sich auf ein konkretes Problem:

„Bestimmen Sie anhand der Anzahl der Vorkommnisse und Ausfälle eines unbekannten Ereignisses, wie hoch die Chance ist, dass sein Eintreten zwischen zwei beliebigen Wahrscheinlichkeitsgraden liegt.“

Mit anderen Worten, nach der Beobachtung eines Ereignisses finden wir den unbekannten ParameterθWie groß ist die Wahrscheinlichkeit zwischen zwei Wahrscheinlichkeitsgraden? Dies ist tatsächlich eines der ersten Probleme in der Geschichte im Zusammenhang mit statistischer Inferenz und führte zu dem Namen inverse Wahrscheinlichkeit. Mathematisch ausgedrückt:

𝑃( 𝜃 | 𝑋）

Dies ist natürlich das, was wir heute die Posterior-Verteilung des Bayes-Theorems nennen.

Unverursachte Ursachen

Lernen Sie diese beiden älteren Pastoren kennen.Thomas BayesUndRichard Price, was die Forschung motiviert hat, ist eigentlich sehr interessant. Doch hierfür müssen wir für einen Moment einige Kenntnisse über Statistik beiseitelassen.

Wir befinden uns im 18. Jahrhundert, und die Wahrscheinlichkeitsrechnung erlangt für Mathematiker zunehmendes Interesse. Mathematiker wie De Moivre oder Bernoulli hatten gezeigt, dass manche Ereignisse mit einem gewissen Grad an Zufälligkeit eintreten, aber dennoch festen Regeln unterliegen. Wenn Sie beispielsweise einen Würfel viele Male werfen, wird er in einem von sechs Fällen auf einer Sechs landen. Es ist, als gäbe es eine verborgene Regel, die das Schicksal des Zufalls bestimmt.

Stellen Sie sich nun vor, Sie seien ein Mathematiker und gläubiger Mensch und lebten in dieser Zeit. Vielleicht interessiert es Sie, in welcher Beziehung diese verborgene Regel zu Gott steht.

Dies ist tatsächlich die Frage, die Bayes und Price selbst gestellt haben. Die Lösung, mit der sie dieses Problem lösen wollten, ließ sich direkt auf den Beweis anwenden, dass „die Welt das Ergebnis von Weisheit und Intelligenz sein muss; damit wird die Existenz Gottes als letzte Ursache bewiesen.“[2] – Das heißt, es gibt keine Ursache und Wirkung.

Laplace

Erstaunlicherweise verfasste der französische Mathematiker Laplace etwa zwei Jahre später, im Jahr 1774, offenbar ohne Thomas Bayes‘ Aufsatz gelesen zu haben, einen Aufsatz mit dem Titel „Über die Ursachen von Ereignissen durch die Wahrscheinlichkeiten von Ereignissen“.[3], ein Aufsatz über das inverse Wahrscheinlichkeitsproblem. Auf der ersten Seite lesen Sie

Die wichtigsten Grundsätze sind:

„Wenn ein Ereignis durch n verschiedene Ursachen verursacht werden kann, dann stehen die Wahrscheinlichkeiten dieser Ursachen für ein bestimmtes Ereignis in einem Verhältnis, das der Wahrscheinlichkeit des Ereignisses bei gegebener Ursache entspricht, und die Wahrscheinlichkeit der Existenz jeder dieser Ursachen ist gleich zur Wahrscheinlichkeit des Ereignisses angesichts der Ursache. Die Wahrscheinlichkeit der Ursachen geteilt durch die Summe der Wahrscheinlichkeiten des Ereignisses angesichts jeder dieser Ursachen.“

Dies ist das, was wir heute als Bayes-Theorem kennen:

​

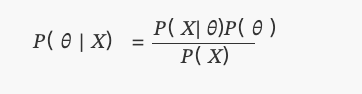
InP(θ)ist gleichmäßig verteilt.

Münzexperiment

Wir werden die Bayessche Statistik in die Gegenwart bringen, indem wir Python und die PyMC-Bibliothek verwenden und ein einfaches Experiment durchführen.

Angenommen, ein Freund gibt Ihnen eine Münze und fragt Sie, ob es Ihrer Meinung nach eine faire Münze ist. Weil er in Eile ist, sagt er Ihnen, dass Sie die Münze nur 10 Mal werfen sollen. Wie Sie sehen, gibt es in diesem Problem einen unbekannten Parameterp, die Wahrscheinlichkeit, bei einem Münzwurf Kopf zu bekommen, und wir wollen diese schätzenpDer wahrscheinlichste Wert von .

(Hinweis: Wir sprechen hier nicht über Parameterpist eine Zufallsvariable, aber dieser Parameter ist fest und wir möchten wissen, zwischen welchen Werten er am wahrscheinlichsten liegt. ）

Um eine andere Perspektive auf dieses Problem zu erhalten, werden wir es unter zwei verschiedenen Gesichtspunkten angehen:

• 1. Sie haben keine Vorabinformationen über die Fairness der Münze und weisen gleiche Wahrscheinlichkeiten zup. In diesem Fall verwenden wir eine so genannte nichtinformative Vorhersage, da Sie Ihrer Überzeugung keine Informationen hinzufügen.
• 1. Sie wissen aus Erfahrung, dass es schwer ist, eine Münze sehr unfair zu machen, auch wenn sie unfair ist. Sie denken also, die ParameterpHöchstwahrscheinlich wird der Wert nicht unter 0,3 oder über 0,7 fallen. In diesem Fall verwenden wir eine informative Vorabinformation.

In beiden Fällen lauten unsere vorläufigen Überzeugungen wie folgt:

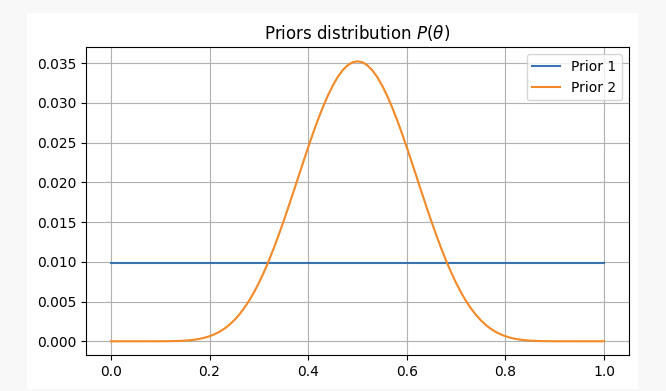
Nach 10 Münzwürfen erhält man 2x Kopf. Mit diesen Beweisen können wir wahrscheinlich herausfinden, wo wir unsere Parameter finden könnenp？

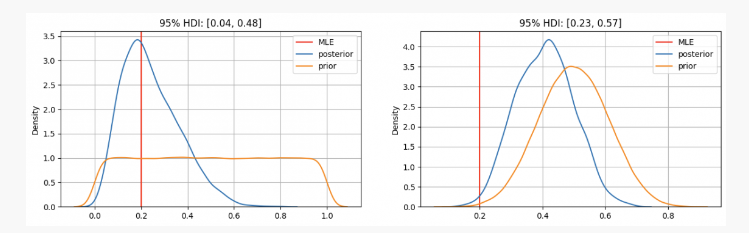
Wie Sie sehen, haben wir im ersten FallpDie vorherige Verteilung von ist auf die Maximum-Likelihood-Schätzung (MLE) zentriert.p=0.2, ein ähnlicher Ansatz unter Verwendung der frequentistischen Methode. Der wahre unbekannte Parameter liegt innerhalb des 95 %-Glaubwürdigkeitsintervalls zwischen 0,04 und 0,48.

Wenn andererseits die Gewissheit besteht, dass der Parameterp Obwohl er zwischen 0,3 und 0,7 liegen sollte, können wir sehen, dass die Posterior-Verteilung bei etwa 0,4 liegt, was viel höher ist als der von unserem MLE ermittelte Wert. In diesem Fall liegt der wahre unbekannte Parameter innerhalb des 95 %-Glaubwürdigkeitsintervalls zwischen 0,23 und 0,57.

Im ersten Fall würden Sie Ihrem Freund also sagen, dass Sie davon überzeugt sind, dass die Münze unfair ist. Aber in einem anderen Fall würden Sie ihm sagen, dass Sie nicht sicher sind, ob die Münze echt ist.

Wie Sie sehen, können die Ergebnisse selbst bei denselben Beweisen (2 Kopf bei 10 Würfen) aufgrund unterschiedlicher Vorannahmen unterschiedlich ausfallen. Dies ist eine Stärke der Bayesschen Statistik, die es uns, ähnlich wie die wissenschaftliche Methode, ermöglicht, unsere Überzeugungen zu aktualisieren, indem wir frühere Überzeugungen mit neuen Beobachtungen und Beweisen kombinieren.

END

Im heutigen Artikel haben wir uns die Ursprünge der Bayesschen Statistik und ihre wichtigsten Vertreter angesehen. Seitdem haben viele weitere wichtige Beiträge zu diesem Statistikbereich beigetragen (Jeffreys, Cox, Shannon usw.), reproduziert von quantdare.com.