FMEX-Sortierung ermöglicht optimale Bestellmengenoptimierung
 0
0
 2308
2308

Der Zusammenbruch von FMEX hat vielen Leuten viel Ärger bereitet, doch vor Kurzem hat das Unternehmen einen Neustartplan vorgelegt und ähnliche Regeln wie beim ursprünglichen Mining formuliert, um die Schulden freizugeben. Es gibt einen Analyseartikel zum Thema Transaction Mining: https://www.fmz.com/bbs-topic/5834. Auch im Sortierbergbau besteht Optimierungsbedarf. Obwohl man nicht zweimal in dieselbe Falle tappen sollte, möchten diejenigen, die Ansprüche auf FMEX haben, möglicherweise darauf zurückgreifen. Bestimmte Echtzeitstrategien, die auf der quantitativen FMZ-Plattform ausgeführt werden können, können ebenfalls veröffentlicht werden.
FMEX-Sortierungs-Entsperrregeln
Definieren Sie alle 5 Minuten jedes Tages als Sortier-Entsperrungszyklus, und jedem Zyklus wird 1⁄288 des Sortier-Entsperrungskontingents des Transaktionspaares an diesem Tag zugewiesen. In jedem Zyklus wird ein zufälliger Zeitpunkt ausgewählt, um eine Momentaufnahme der Kauf- und Verkaufsaufträge des Handelspaares zu erstellen. Dabei gilt:
- Kaufen 1 Basierend auf dem Anteil des Benutzerbestellbetrags wird 1⁄4 des Rückgabebetrags des Entsperrzeitraums diesem Ranking zugewiesen
- Verkaufen 1 Entsprechend dem Anteil der Benutzerbestellmenge wird 1⁄4 des Rückgabebetrags des Entsperrzeitraums diesem Ranking zugewiesen
- Für die 4 Stufen „2 kaufen“ bis „5 kaufen“ wird jeder Stufe 1⁄40 des Rückgabebetrags des Entsperrungszeitraums entsprechend dem Anteil des Bestellbetrags des Benutzers an jeder Stufe zugewiesen.
- Für die Bestellungen in den 4 Verkaufsstufen 2 bis 5 wird 1⁄40 des Rückgabebetrags des Freischaltzeitraums der Rangliste entsprechend dem Anteil der Bestellmenge des Benutzers in jeder Stufe zugeteilt.
- Bei den fünf Bestellungen von „Kauf 6“ bis „Kauf 10“ wird jeder Bestellung entsprechend dem Anteil der Bestellmenge an der jeweiligen Bestellung 1⁄50 des Rücknahmebetrags der Entsperrfrist zugeteilt.
- Bei den fünf Bestellungen von 6 bis 10 wird jeder Bestellung 1⁄50 des Rücknahmebetrags der Entsperrfrist entsprechend dem Anteil der Bestellsumme an der jeweiligen Bestellung zugeteilt.
- Bei den fünf Bestellungen von Kauf 11 bis Kauf 15 wird jeder Bestellung entsprechend dem Anteil der Bestellmenge an der jeweiligen Bestellung 1⁄100 des Rücknahmebetrags der Entsperrfrist zugeteilt.
- Für die fünf Aufträge von Verkauf 11 bis Verkauf 15 wird jedem Auftrag 1⁄100 des Rückgabebetrags des Entsperrungszeitraums entsprechend dem Anteil des Auftragsbetrags in jedem Auftrag zugeteilt.
Der Gesamtertrag aus der Ranglistenfreischaltung eines Benutzers in einem bestimmten Handelspaar am selben Tag ist die Summe der Beträge, die dem Benutzer für die Ranglistenfreischaltung in jedem Zyklus des Handelspaares zurückgegeben werden.
Sortieren, um Vorteile freizuschalten
Erstens betragen die Gesamteinnahmen aus dem Sortieren und Entsperren:
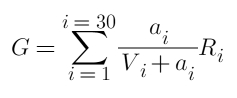
Dabei stellt i eine der Positionen dar, insgesamt gibt es für beide Parteien 30 Positionen, a ist die ausstehende Bestellmenge, R ist der freizugebende Rückgabebetrag und V ist die Gesamtzahl der bestehenden Bestellungen.
Im Gegensatz zum Freigeben von Transaktionen ist das Aufgeben einer Bestellung kostenlos. Hier muss R nur die relative Größe berücksichtigen, und der absolute Betrag in USDT muss nicht berücksichtigt werden. Wenn wir die Gesamtzahl der ausstehenden Aufträge ermitteln, stellt sich die Frage, wie die Aufträge den verschiedenen Positionen zugewiesen werden können, um den Gewinn G zu maximieren. Einfach den Standort mit der geringsten Bestellmenge zu suchen und alle Bestellungen dort zu platzieren, ist offensichtlich nicht die optimale Lösung. Beispielsweise gibt es drei Positionen mit 10 bestehenden Aufträgen und ihr R ist gleich. Wir setzen das Gesamtauftragsvolumen auf 30. Wenn wir nur eine Position für die Auftragserteilung auswählen, beträgt der endgültige Gesamtgewinn 0,75R. 10, die Der endgültige Gewinn beträgt 1,5 R. Dies zeigt, dass der Gewinn bei verteilten Aufträgen manchmal besser ist. Wie verteilen Sie also die Mittel?
Optimierung der Sortierungsfreigabe
Abschließend sind unsere Optimierungsziele und Einschränkungen:
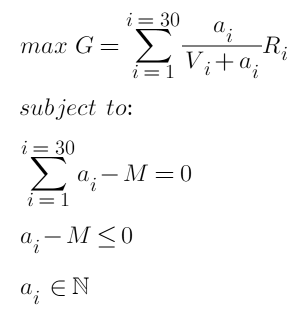
Wobei M die Gesamtbestellmenge ist. Dies ist ein quadratisches konvexes Optimierungsproblem mit Ungleichungen, das die KTT-Bedingung erfüllt und eine ganzzahlige Lösung hat. Mithilfe des entsprechenden Pakets und des konvexen Optimierungssolvers sollte es möglich sein, die Ergebnisse direkt abzurufen und für jede Position die optimale Bestellmenge zurückzugeben. Aber das ist offensichtlich nicht die Antwort, die wir wollen. Wir müssen das Problem vereinfachen und konkrete Lösungsschritte finden.
Beginnen wir mit einem einfachen Beispiel
Betrachten Sie nur zwei Ebenen. Die aktuellen Auftragsvolumina betragen 10 und 20 (bezeichnet als erste bzw. zweite Ebene). Ihre Freigabequoten sind beide R. Die Gesamtzahl der Strategie-Reserveaufträge beträgt 30. Wie sollten sie zugeteilt werden? Wurde der freigegebene Geldbetrag maximiert? Diese Frage scheint einfach, aber ohne Berechnung ist es schwierig, die richtige Schlussfolgerung zu ziehen. Die Leser sollten zunächst selbst über die Antwort nachdenken.
Szenario 1:
Suchen Sie die Mindestbestellposition und platzieren Sie alle Bestellungen dort. Der Gesamtgewinn G=30/(30+10)=0,75R. Dies ist auch die einfachste Lösung, die man sich vorstellen kann.
Szenario 2:
Jedes Mal wird 1 Yuan zugeteilt und zwar dem Ort, der den größten Gewinn abwerfen kann, also dem Ort mit der geringsten Anzahl ausstehender Aufträge. Dann wird der erste Yuan der ersten Stufe zugeteilt, und das Auftragsvolumen der ersten Stufe beträgt 10+1. Der zweite Yuan wird ebenfalls der ersten Stufe zugeteilt … und so weiter, bis insgesamt 10 Yuan zusammenkommen. wird der ersten Stufe zugewiesen. Zu diesem Zeitpunkt wird Einer nach dem Zufallsprinzip ausgewählt, und wenn die Gesamtzahl der ausstehenden Aufträge in der ersten Stufe 20 übersteigt, wird er der zweiten Stufe zugewiesen. Das Endergebnis ist, dass der ersten Stufe 20 Yuan und der zweiten Stufe 10 Yuan zugeteilt werden und ihre endgültigen Bestellungen jeweils 30 betragen. Gesamtgewinn G = 20⁄30 + 10⁄30 = R. Diese Lösung ist viel besser als Lösung 1 und lässt sich auch einfacher berechnen.
Szenario 3:
Wir können davon ausgehen, dass der ersten Stufe a zugewiesen ist und der zweiten Stufe 30-a. Dann können wir die Gleichung direkt auflisten und ihre Ableitung als 0 finden (der Prozess ist hier nicht aufgeführt, er ähnelt dem Artikel über die Transaktionsfreigabe ) und berechnen Sie das Endergebnis. Die Formel lautet:
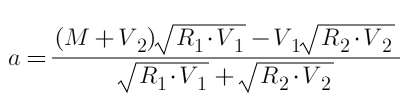
Ersetzen Sie die Ganzzahl und erhalten Sie a=15. Der Gesamtgewinn G = 15⁄25 + 15⁄35 = 1,0286 R ist besser als Option 2. Da es direkt aus der Formel abgeleitet wird, ist dies die optimale Lösung. Die Leser können es nachlesen.
Das Ergebnis kann anders ausfallen als erwartet. Es ist offensichtlich, dass die Zuteilung jedes Dollars in Plan 2 unter den gegenwärtigen Umständen die optimale Lösung ist. Warum ist es nicht insgesamt die optimale Lösung? Diese Situation kommt sehr häufig vor. Das lokale Optimum ist nicht unbedingt das Gesamtoptimum, da die Aufträge vor der Zuteilung bereits Mittel investiert hatten und die Gesamteffizienz die versunkenen Kosten berücksichtigen muss. Unser Ziel bei jedem Optimierungsschritt besteht in der Maximierung der Gesamteffizienz und nicht in der Maximierung eines einzelnen Vorteils.
Spezifischer Optimierungsplan
Schließlich haben wir mit der tatsächlich durchführbaren Operation begonnen. Vereinfachen wir das Problem, indem wir jedes Mal 1 Yuan zuweisen. Messen wir zunächst die Effizienz. Die Ableitung kann den Beitrag jedes a zu G widerspiegeln. Dieser Beitrag berücksichtigt die kumulierten Kosten und nicht den Nutzen einer einzelnen Verteilung. Je größer der Wert, desto größer der Gesamtbeitrag zum endgültigen Nutzen . Gemäß der Grafik der Funktion ist die Effizienz offensichtlich bei a = 1 von Existenz bis Nichtexistenz am höchsten und nimmt dann allmählich ab.
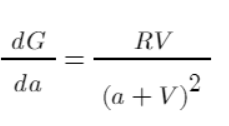
Am Beispiel des obigen einfachen Beispiels können wir die Effizienz der Mittelzuweisung berechnen und in einer Tabelle auflisten:
| Mittel | 1 | 2 |
|---|---|---|
| 1 | 0.0826 | 0.0454 |
| 2 | 0.069 | 0.0413 |
| 3 | 0.0592 | 0.0378 |
| 4 | 0.051 | 0.0347 |
| 5 | 0.0444 | 0.032 |
| … | … | … |
|12 | 0.0207 |0.0195| |13 | 0.0189 |0.0184| |14 | 0.0174 |0.0173| |15 | 0.016 |0.0163| |16 | 0.0148 |0.0154| |17 | 0.0137 |0.0146| |18 | 0.0128 |0.0139|
Gemäß der Tabelle wird der erste Yuan der ersten Stufe zugeteilt, der zweite Yuan der ersten Stufe… der fünfte Yuan der zweiten Stufe… und so weiter, und schließlich werden 15 Yuan zugeteilt an die erste Stufe und 15 Yuan für die zweite Stufe. Yuan, was zufällig die optimale Lösung ist, die wir basierend auf der Gleichung berechnet haben. Insbesondere für den 30. Gang ist der Algorithmus derselbe und die spezifischen Schritte sind:
- 1. Überprüfen Sie zuerst alle Gänge. Wenn V = 0, dann ist a = 1 und es werden keine weiteren Mittel zugewiesen.
- 2. Teilen Sie die Gesamtmittel in N Teile auf und wählen Sie jedes Mal einen Gang für die Aufteilung aus.
- 3. Berechnen Sie die Effizienz jedes Gangs = RV/pow(a+V,2), wobei a die der Position zugewiesenen kumulierten Mittel + die diesmal zugewiesenen Mittel darstellt.
- 4. Weisen Sie die Mittel der effizientesten Ausrüstung zu und wählen Sie nach dem Zufallsprinzip eine aus, wenn die Effizienz gleich ist.
- 5. Wiederholen Sie 3-4, bis die Mittel zugewiesen sind
Wenn unser Gesamtauftragsvolumen groß ist, ist es zu ineffizient, jeden Dollar einzeln zuzuweisen. Wir können die Mittel in 100 Teile aufteilen und jeweils einen Teil zuweisen. Da es sich nur um eine einfache Berechnung und Sortierung handelt, ist der Algorithmus sehr effizient. Insbesondere auf der Ausführungsebene gibt es noch Optimierungspotenzial, beispielsweise durch die Aufteilung unserer Aufträge in 100 Stück, sodass wir bei jeder Anpassung die Aufträge nur neu zuordnen müssen, anstatt sie alle zu stornieren. Sie können den R-Wert auch selbst festlegen und denjenigen, die weit vom Markt entfernt sind, mehr Gewicht geben. Wenn es Überschneidungen zwischen der Freigabe der Sortierung und der Freigabe der Pending-Order gibt, können Sie diese gemeinsam berücksichtigen und so weiter.
Dieser Artikel ist ein Originalartikel der FMZ Quantitative Platform. Bitte geben Sie bei der Übertragung die Quelle an: https://www.fmz.com/bbs-topic-new/5843