Nota: Este caso es para uso de estudio y investigación y no constituye una recomendación de inversión.

Los datos de precios de Bitcoin están basados en una secuencia de tiempo, por lo que la mayoría de las predicciones de precios de Bitcoin se realizan utilizando el modelo LSTM.

La memoria a corto y largo plazo (LSTM) es un modelo de aprendizaje profundo especialmente adecuado para datos de secuencia temporal (o datos con una secuencia temporal / espacial / estructurada, como películas, oraciones, etc.) y es el modelo ideal para predecir la dirección del precio de las criptomonedas.

Este artículo se centra en la comparación de datos a través de LSTM para la predicción del precio futuro de Bitcoin.

Repositorios que import requiere

import pandas as pd
import numpy as np

from sklearn.preprocessing import MinMaxScaler, LabelEncoder
from keras.models import Sequential
from keras.layers import LSTM, Dense, Dropout

from matplotlib import pyplot as plt
%matplotlib inline

Análisis de datos

Carga de datos

Leer los datos del día de BTC

data = pd.read_csv(filepath_or_buffer="btc_data_day")

En la actualidad, hay 1380 columnas de datos disponibles, que se componen de columnas de fecha, abierto, alto, bajo, cerrado, volumen (BTC), volumen (moneda) y precio ponderado. A excepción de la columna de fecha, el resto de las columnas de datos son del tipo de datos float64.

data.info()

Vean las primeras 10 líneas de datos.

data.head(10)

Visualización de datos

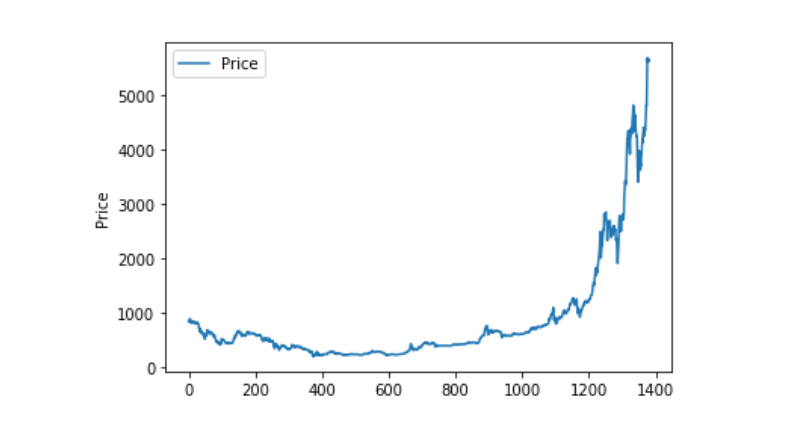
Utilizando matplotlib, trazamos el precio ponderado para ver la distribución y el movimiento de los datos. En el gráfico encontramos una parte de los datos 0 y necesitamos confirmar si hay excepciones en los datos.

plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()

Tratamiento de datos anormales

Primero, veamos si los datos contienen datos de nan, y veremos que no hay datos de nan en nuestros datos.

data.isnull().sum()

Date                 0
Open                 0
High                 0
Low                  0
Close                0
Volume (BTC)         0
Volume (Currency)    0
Weighted Price       0
dtype: int64

Ahora vamos a ver los datos de 0 y veremos que los datos tienen valores de 0 que necesitamos procesar.

(data == 0).astype(int).any()

Date                 False
Open                  True
High                  True
Low                   True
Close                 True
Volume (BTC)          True
Volume (Currency)     True
Weighted Price        True
dtype: bool

data['Weighted Price'].replace(0, np.nan, inplace=True)
data['Weighted Price'].fillna(method='ffill', inplace=True)
data['Open'].replace(0, np.nan, inplace=True)
data['Open'].fillna(method='ffill', inplace=True)
data['High'].replace(0, np.nan, inplace=True)
data['High'].fillna(method='ffill', inplace=True)
data['Low'].replace(0, np.nan, inplace=True)
data['Low'].fillna(method='ffill', inplace=True)
data['Close'].replace(0, np.nan, inplace=True)
data['Close'].fillna(method='ffill', inplace=True)
data['Volume (BTC)'].replace(0, np.nan, inplace=True)
data['Volume (BTC)'].fillna(method='ffill', inplace=True)
data['Volume (Currency)'].replace(0, np.nan, inplace=True)
data['Volume (Currency)'].fillna(method='ffill', inplace=True)

(data == 0).astype(int).any()

Date                 False
Open                 False
High                 False
Low                  False
Close                False
Volume (BTC)         False
Volume (Currency)    False
Weighted Price       False
dtype: bool

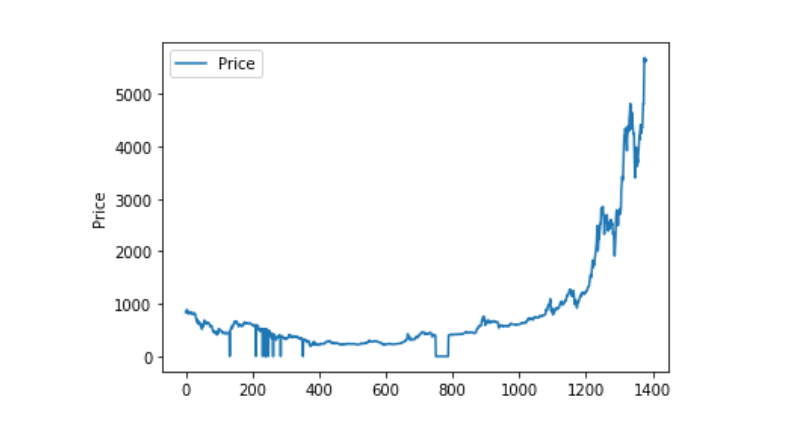
Y luego vemos la distribución y el movimiento de los datos, y en este punto la curva es muy continua.

plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()

Separación de los conjuntos de datos de entrenamiento y de prueba

Unificar los datos en 0-1

data_set = data.drop('Date', axis=1).values
data_set = data_set.astype('float32')
mms = MinMaxScaler(feature_range=(0, 1))
data_set = mms.fit_transform(data_set)

Separando el conjunto de pruebas y el conjunto de entrenamiento en 2:8

ratio = 0.8
train_size = int(len(data_set) * ratio)
test_size = len(data_set) - train_size
train, test = data_set[0:train_size,:], data_set[train_size:len(data_set),:]

Creación de conjuntos de datos de entrenamiento y pruebas con un día como período de ventana para crear nuestros conjuntos de datos de entrenamiento y pruebas.

def create_dataset(data):
    window = 1
    label_index = 6
    x, y = [], []
    for i in range(len(data) - window):
        x.append(data[i:(i + window), :])
        y.append(data[i + window, label_index])
    return np.array(x), np.array(y)

train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)

Definición y entrenamiento del modelo

Esta vez usamos un modelo simple que tiene la siguiente estructura:. LSTM2. Dense。

En este caso, el valor de los pasos de tiempo es el intervalo de la ventana de tiempo de la entrada de datos. Aquí usamos 1 día como ventana de tiempo, y nuestros datos son datos diarios, por lo que nuestros pasos de tiempo son 1 .

La memoria larga a corto plazo (LSTM) es un tipo especial de RNN, principalmente para resolver el problema de la desaparición de la escala y la explosión de la escala en el entrenamiento de secuencias largas.

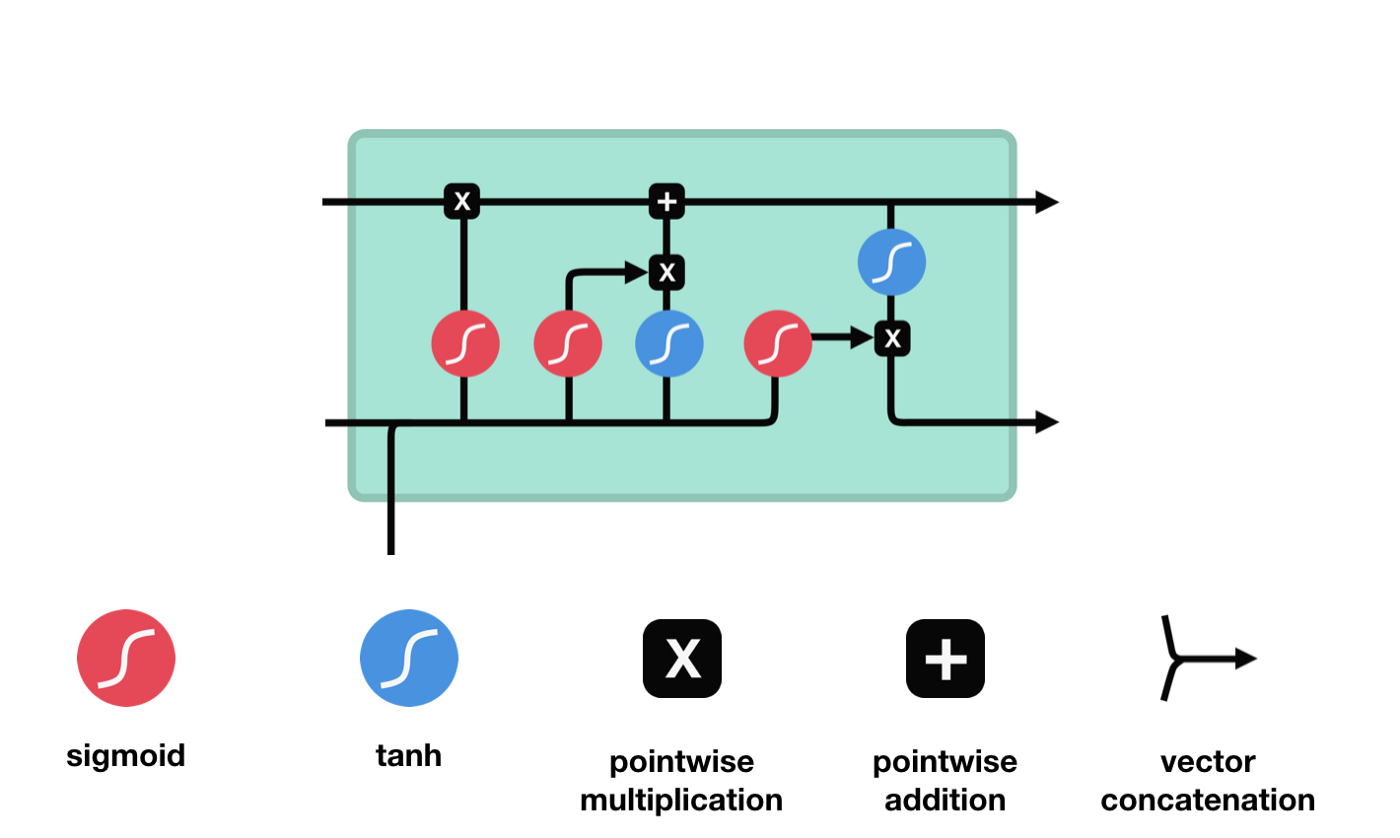
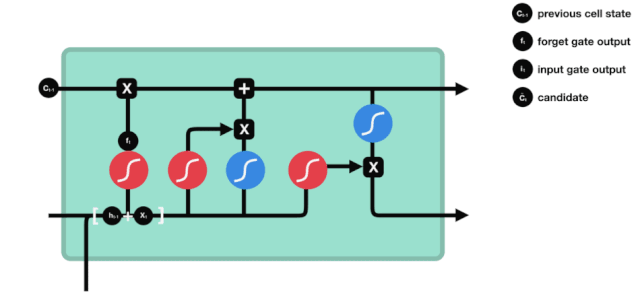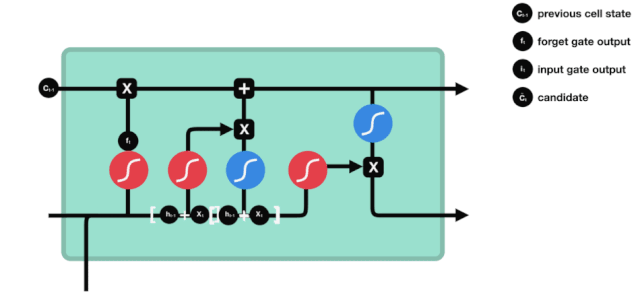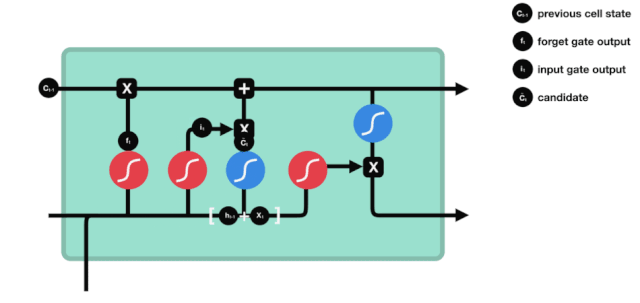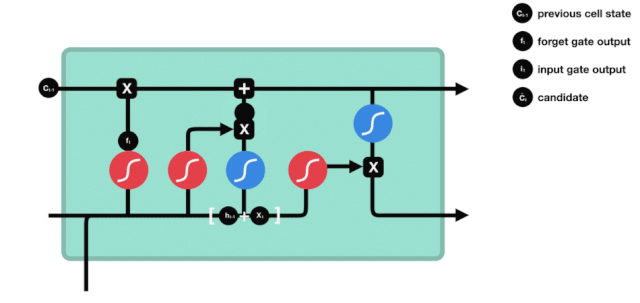
Se puede ver en el diagrama de la estructura de la red de LSTM que LSTM es en realidad un modelo pequeño que contiene 3 funciones de activación sigmoide, 2 funciones de activación tanh, 3 multiplicaciones y 1 suma.

Estado de la célula

El estado celular es el núcleo de LSTM, es la línea negra en la parte superior de la imagen, debajo de esta línea negra hay algunas puertas, que se presentan a continuación. El estado celular se actualizará según los resultados de cada puerta.

Las redes LSTM pueden eliminar o agregar información al estado celular a través de una estructura llamada puerta. La puerta puede decidir selectivamente qué información dejar pasar. La estructura de la puerta es una combinación de una capa sigmoide y una operación de multiplicación de puntos.

La puerta del olvido

El primer paso del LSTM es decidir qué información necesita ser desechada por el estado celular. Esta parte de la operación es manejada por una unidad sigmoide llamada puerta del olvido.

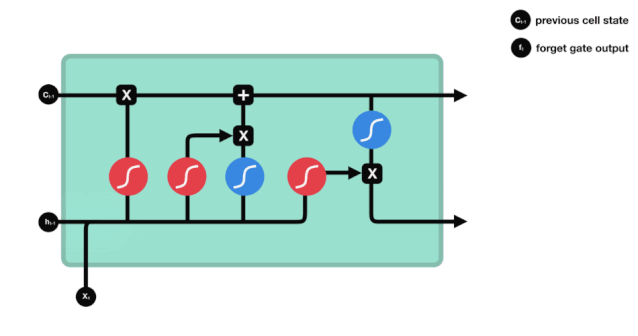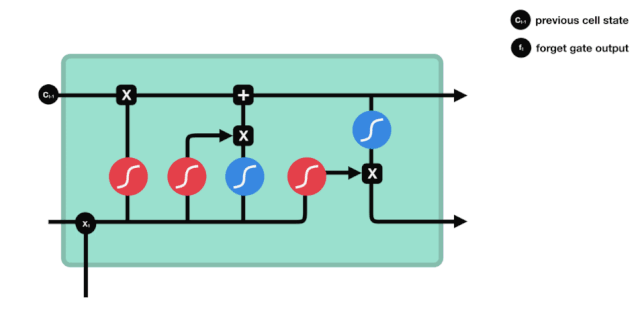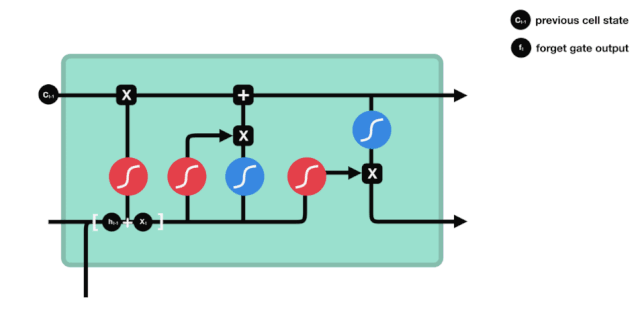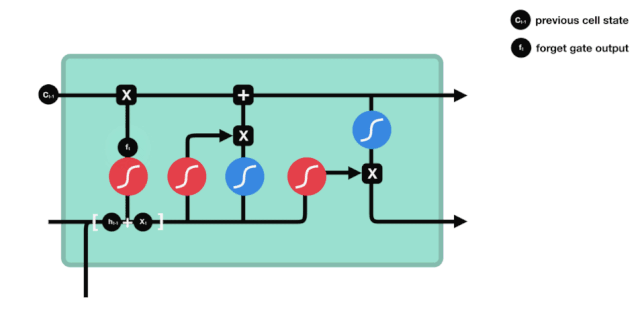
Podemos ver que la puerta de olvido, al ver la información \(h_{l-1}\) y \(x_{t}\), produce un vector entre 0 y 1, donde el valor de 0 a 1 indica qué información se conserva o se descarta en el estado de la célula \(C_{t-1}\). 0 indica que no se conserva y 1 indica que se conserva.

La expresión matemática es \(f_{t}=\sigma\left(W_{f} \cdot\left[h_{t-1}, x_{t}\right]+b_{f}\right)\)

Puerta de entrada

El siguiente paso es decidir qué nueva información se añade al estado de la célula, lo cual se hace mediante la introducción y apertura de la puerta.

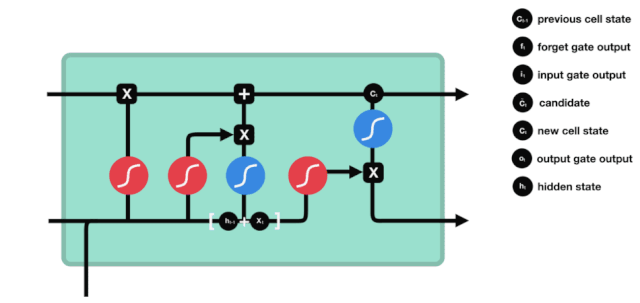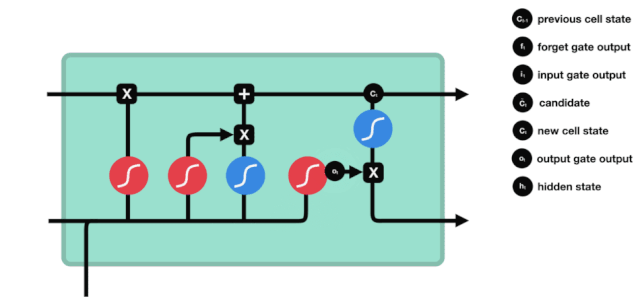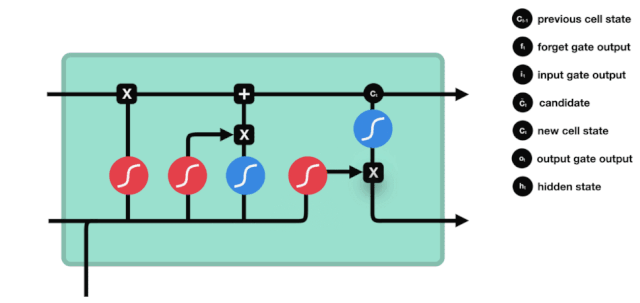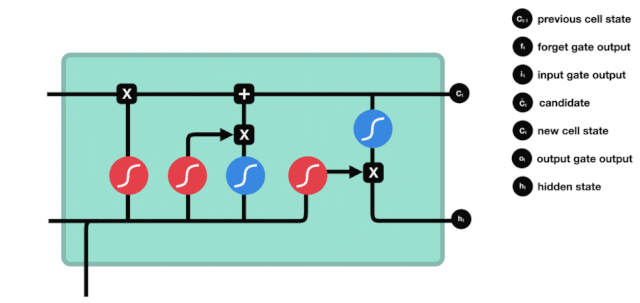
Vemos que \(h_{l-1}\) y \(x_{t}\) se colocan en una puerta de olvido (sigmoid) y en una puerta de entrada (tanh). Como la puerta de olvido tiene un valor de 0-1, si la puerta de olvido es 0, el resultado posterior a la puerta de entrada \(C_{i}\) no se agregará al estado de la célula actual, si es 1, todo se agregará al estado de la célula, por lo que la puerta de olvido tiene la función de agregar selectivamente el resultado de la puerta de entrada al estado de la célula.

La fórmula matemática es \(C_{t}=f_{t} * C_{t-1}+i_{t} *\tilde{C}_{t}\)

Puertas de salida

Después de actualizar el estado de la célula se necesita la suma de \(h_{l-1}\) y \(x_{t}\) para determinar qué características de estado de la célula de salida, aquí se necesita que la entrada sea juzgada a través de una capa sigmoide llamada puerta de salida, y luego que el estado de la célula sea juzgado a través de la capa tanh para obtener un vector de valor entre -1 ~ 1, que se multiplica por el criterio obtenido por la puerta de salida para obtener la salida de la unidad final de RNN. La intención de la animación es la siguiente

def create_model():
    model = Sequential()
    model.add(LSTM(50, input_shape=(train_x.shape[1], train_x.shape[2])))
    model.add(Dense(1))
    model.compile(loss='mae', optimizer='adam')
    model.summary()
    return model

model = create_model()

history = model.fit(train_x, train_y, epochs=80, batch_size=64, validation_data=(test_x, test_y), verbose=1, shuffle=False)

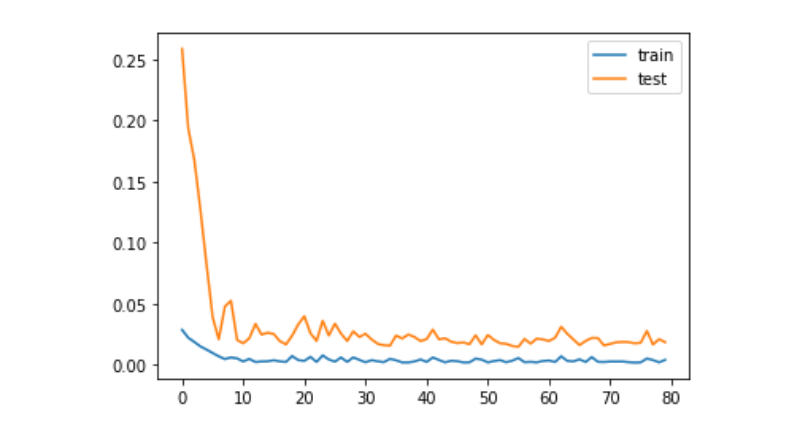
plt.plot(history.history['loss'], label='train')
plt.plot(history.history['val_loss'], label='test')
plt.legend()
plt.show()

train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)

Las predicciones

predict = model.predict(test_x)
plt.plot(predict, label='predict')
plt.plot(test_y, label='ground true')
plt.legend()
plt.show()

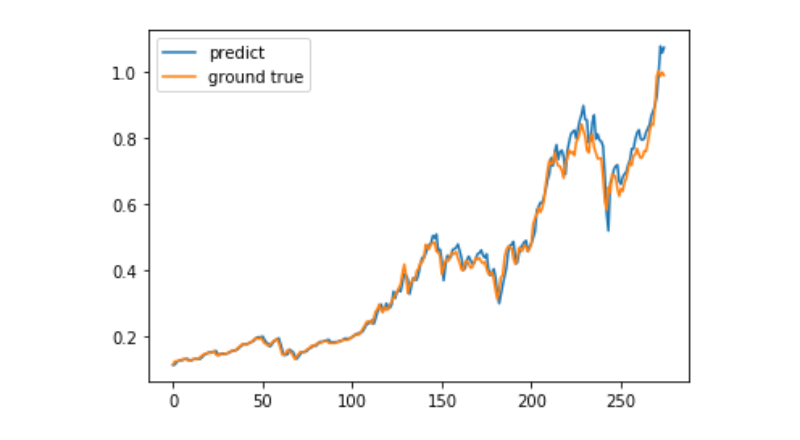
Actualmente, el uso de aprendizaje automático para predecir el movimiento del precio a largo plazo de Bitcoin es muy difícil, y este artículo solo puede usarse como un caso de estudio. El caso luego se pondrá en línea con imágenes de demostración de la nube de Matrix, para que los usuarios interesados puedan experimentar directamente.