Declaración de derechos de autor: si necesita reproducir el código de este artículo, indique la fuente, si es para uso comercial, escriba un artículo por correo electrónico o comuníquese con el autor al correo electrónico [email protected]

1. Introducción

Las ventajas de las transacciones cuantitativas

El comercio cuantitativo se refiere al juicio subjetivo hecho por el hombre en lugar de modelos matemáticos avanzados, que utilizan la tecnología informática para elaborar estrategias que utilizan una gran cantidad de datos históricos para crear una gran cantidad de eventos de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad de probabilidad “La moneda digital es un medio de comunicación, un medio de comunicación que permite a las personas acceder a información y a los servicios de los demás.*La continuidad del mercado de transacciones de 7 horas ininterrumpidas, y el comercio cuantitativo puede alcanzar el efecto del comercio de alta frecuencia, desde el mercado de monedas digitales es obviamente un buen comienzo para la cuantificación. El mercado de monedas digitales es aún inmaduro.

Descripción del modelo GQNR

Este modelo es basado en el modelo de Garch para la predicción de la volatilidad, y utiliza la regresión no lineal para predecir la volatilidad a través de la regresión decimal de los valores de VaR, como la regresión GA para predecir el VaR superior y el VaR inferior en el próximo ciclo futuro. En el contexto, este método se llama GQNR.

1. El módulo Garch

        Este módulo explicará en detalle las derivaciones del núcleo de la estrategia Garch, que tiene cierta aplicabilidad en los mercados financieros y puede alcanzar cierto efecto predictivo en las monedas digitales.

1.1 Definición de Garch

La esencia del modelo ARCH es que el plano móvil de grado q de la secuencia cuadrada de residuos se ajusta al valor de la función de diferenciación en ese momento. Debido a que el modelo de promedio móvil tiene una intersección de grado q del coeficiente de correlación automática, el modelo ARCH en realidad solo se aplica a los coeficientes de correlación automática a corto plazo de la función de diferenciación automática.          Pero en la práctica, algunas secuencias de residuos de la función de diferencia de diferencia son de interés a largo plazo, cuando se utiliza el modelo de ARCH para ajustar la función de diferencia de diferencia de diferencia, se producirá una muy alta promedio móvil, aumentar la dificultad de la estimación de los parámetros y, finalmente, afectar a la precisión de ajuste del modelo ARCH.                                                                                                                                                         El modelo GARCH es en realidad basado en ARCH, que se forma mediante la regresión de la clase p de la función diferencial que se considera, y que puede adaptarse eficazmente a la función diferencial con memoria a largo plazo. El modelo ARCH es un ejemplo particular del modelo GARCH, el modelo GARCH (p,q) de p = 0.

1.2 Proceso ARCH

       definido como σn en el ciclo de negociación n-1 para estimar la volatilidad de los activos en el ciclo de negociación n, mu es el rendimiento diario, entonces se puede hacer una estimación no sesgada en función del rendimiento de los últimos m ciclos de negociación: $\( \sigma *n^2= \frac{1}{m-1} \sum\limits*{i=1}^m {( { \mu_{n-i}- \overline{\mu} } ) ^2}, \)\(         Hacer los siguientes cambios: 1 convertirá μn-i en porcentaje de rentabilidad; 2 convertirá m-1 en m; 3 supongamos que μ = 0, y estos cambios no afectan mucho a los resultados. De acuerdo con la fórmula anterior, la tasa de fluctuación se puede simplificar como: \)\( \sigma *n^2= \frac{1}{m} \sum\limits*{i=1}^m { \mu_{n-i} ^2}, \)\(         es decir, el cuadrado de la tasa de fluctuación de cada período tiene un peso igual 1/m, ya que es la estimación de la tasa de fluctuación actual, los datos más cercanos deben ser asignados un peso más alto, entonces la fórmula se puede cambiar a: \)\( \sigma *n^2= \sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}, \)$         αi es el coeficiente de la rentabilidad cuadrada del ciclo de negociación i, tomando valores positivos y el menor valor de i, la suma de los pesos es 1. Para una extensión adicional, suponiendo que exista una diferencia de tasa de variación de largo plazo VL, y el peso correspondiente es γ, se obtiene según la fórmula anterior:

\[ \begin{cases}\sigma *n^2= \gamma V*{L}+\sum\limits_{i=1}^m { \alpha_i\mu_{n-i} ^2}\ &\ \gamma+\sum\limits_{i=1}^m{\alpha_i\mu_{n-i}^2}=1 & \end{cases} , \]

        el formulario 15 puede ser reescrito como: $\( \sigma *n^2= \omega+\sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}, \)\(         De acuerdo con la fórmula anterior podemos obtener el proceso ARCH común \)\( \sigma *n^2= \omega+{ \alpha\mu*{n-1} ^2}, \)$

1.3 El proceso de GARCH

El modelo GARCH (p,q) es una combinación de los modelos ARCH (p) y EWMA (q), en el sentido de que la volatilidad está relacionada no solo con los ingresos de la etapa anterior p, sino también con la etapa anterior q, expresada de la siguiente manera: $\( \sigma *n^2= \omega+\sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}+\sum\limits_{i=1}^m { \beta_i\sigma_{n-i} ^2}, \)\(         De acuerdo con la fórmula anterior podemos obtener el común GARCH ((1,1)): \)\( \begin{cases}\sigma *n^2= \omega+{ \alpha\mu*{n-1} ^2+\beta\sigma_{n-1}^2}\&\ \qquad\alpha+\beta+\gamma=1 & \end{cases} , \)$

2 módulos QR

        Esta sección explicará la regresión de fracciones básica y la importancia de las fracciones estratégicas

Definición de QR

        La regresión numérica fraccionaria es un método de modelado para estimar la relación lineal entre un conjunto de variables de regresión X y los dígitos de la variable interpretada Y. Los modelos de regresión anteriores en realidad estudian las expectativas condicionales de las variables que se explican. También se preocupa por la relación entre la variable explicada y el promedio de la distribución de la variable explicada. Fue propuesto por primera vez por Koenker y Bassett en 1978.

2.2 Desde OLS hasta QR

El método de regresión general es el método de minimizar la ecuación, es decir, el cuadrado de la suma de minimizar el error: $\( min \sum{({y_i- \widehat{y}*i })}^2 \)\(         y el objetivo de la fracción es minimizar el valor absoluto de error ponderado sobre la base de la fórmula anterior y: \)\( \mathop{\arg\min*\beta}\ \ \sum{[{\tau(y_i-X_i\beta)^++(1-\tau)(X_i\beta-y_i) ^+ }]} \)$

2.2 Visualización de QR

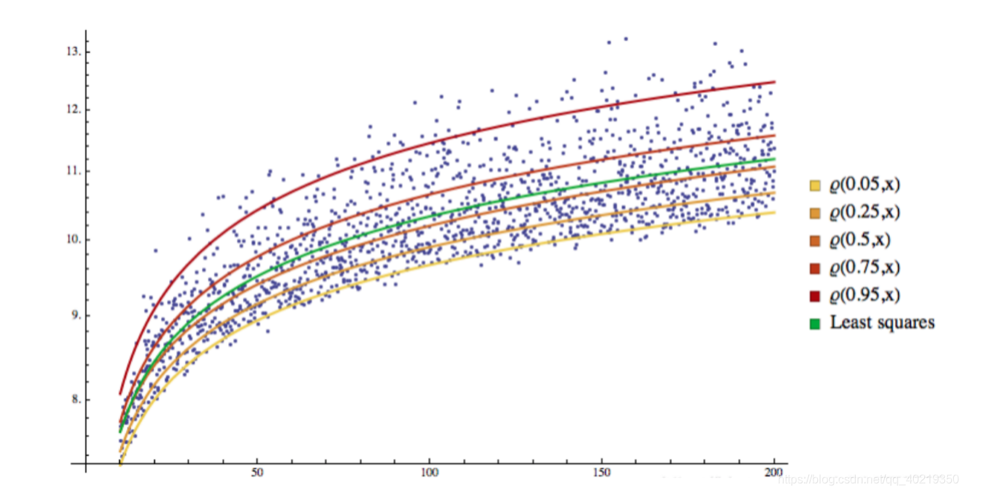
3. Regresión de GARCH-QR

Es natural que pensemos si es posible usar sigma de fluctuación de mercado desconocido y el parámetro Q, VaR, para hacer una regresión para predecir la probabilidad de que el futuro se mueva en la dirección en que se desarrollará este sector.

3.1 Selección de la tasa de fluctuación y la forma de regreso de VaR

        Como aquí se trata de un núcleo estratégico, voy a citar un formulario para ilustrar el pensamiento. $\( VaR=\epsilon+W^TE\E=(\zeta,\zeta^2,\zeta^3,\zeta^4)\W=(W_1,W_2,W_3,W_4) \)$

3.2 Determinación de la función objetivo

        Basado en la información anterior, podemos combinar y obtener la función objetivo final para optimizar: $\( \widehat{W}=\mathop{\arg\min_W}\ \ \sum{[{\alpha(VaR_t-W^TE_t)^++(1-\alpha)(W^TE_t-VaR_t) ^+ }]} \)$

3.3 Optimización de la función objetivo con aprendizaje automático

        Este paso es más opcional, la escala tradicional se reduce, también se puede heredar el algoritmo, el lector puede ejercer su propia creatividad para experimentar.Hay algo acerca de la dirección de algoritmos GA

3 Cómo usar GQNR en la cuantificación

1. Determinación de las ideas

       GQNR se centra en la volatilidad del mercado, en cada momento del período actual, se puede hacer un pronóstico de la volatilidad de la siguiente etapa a través de GARCH, por otro lado, mediante el regreso decimal de la volatilidad de la predicción de datos pasados, se puede obtener un umbral de fluctuación que no excederá en la mayor parte de las probabilidades de los límites superiores y inferiores.

2. Dificultades en su uso

• Tomando la forma de regreso
• Opciones de algoritmos adaptativos
• Los parámetros adecuados para el aprendizaje automático
• La incertidumbre y la aleatoriedad del mercado

3. La solución

• Reducir el ciclo de aprendizaje de estrategias
• Reducción de la garantía de depósito individual frente al riesgo a largo plazo
• Aumento de la co-verificación de tendencias de doble línea media y la confirmación de la segunda desvalorización