PS: Este post es largo, no es muy extenso, te recomiendo que lo leas con paciencia, seguro que te será de utilidad.

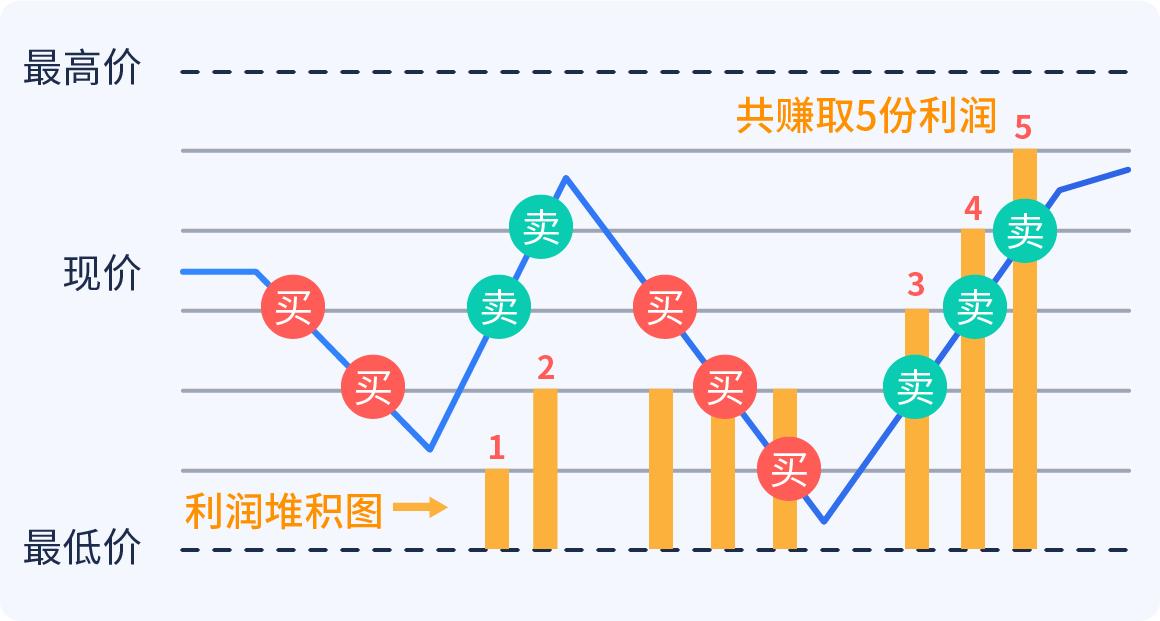
El método de negociación de la rejilla es esencialmente una operación mecánica de compra y venta, mediante la repetición de la operación de compra y venta de precios de baja y alta frecuencia. Cuando los precios bajan, se compra por categorías, y cuando los precios suben, se vende por categorías. El método de negociación de la rejilla no depende del pensamiento artificial, sino que es completamente un acto de procedimiento, como la red de pesca, que utiliza las fluctuaciones de la situación para comprar y vender en el intervalo de la rejilla, para obtener ganancias a través de la repetición del ciclo de diferencia de precios.

El método de negociación de la red puede ser programado, no se necesita una liquidación prolongada, la seguridad y la estabilidad de los ingresos, por lo que el método de negociación de la red es el método de ganancias estables más adecuado para la participación de la gente común, ya que este método requiere poca experiencia en las habilidades humanas, es muy versátil y es especialmente adecuado para los amigos que no pueden ganar dinero en el mercado de valores.

Las reglas de transacción de la ley de transacción de la red

Una simple comparación: es dividir su dinero en dos partes iguales: una parte para comprar inmediatamente las acciones o fondos que usted vea, y la otra parte en el bolsillo de reserva. Si las acciones o fondos que usted compra siguen cayendo, usted saca el dinero de su bolsillo y lo deposita; por el contrario, si las acciones o fondos que usted compra se caen, venda una parte de ellos y ponga el dinero en su bolsillo. Muchos de los programas de negociación están integrados, los usuarios pueden automatizar el funcionamiento con solo configurarlos, la serie de artículos de la columna de la columna de la columna de la columna de la columna de la columna de la columna de la columna de la columna de la columna de la columna de la columna de la columna de la columna de la columna de la columna de la columna de la columna de la columna de la columna de la columna de la columna de la columna de la columna de la columna de la columna de la columna de la columna.

Hay muchas variantes de la estrategia de la red, y una de las más conocidas es la siguiente, que explica el principio científico de ganar dinero de forma estable y explica por qué tu cuenta se va volviendo más y más rica.

Todos los que han comprado acciones han tenido esta experiencia, una acción subió con dificultad, luego cayó de nuevo al precio original, sin esfuerzo, se arrepintió y vendió pronto. De hecho, no hay necesidad de arrepentirse, uno de los más grandes científicos del mundo, el inventor de la informática Shannon, nos ayudó a encontrar una solución.

Durante la segunda mitad de su vida, Shannon se dedicó principalmente a la investigación de inversiones, y a menudo dio conferencias para enseñar a la gente los secretos. Un año, Shannon dio una charla en el auditorio más grande de MIT para enseñar a la gente los secretos de cómo ganar dinero en la situación mencionada anteriormente.

Los seguidores de este enigma lo llaman el diablo de Shannon, y el diablo de Shannon es una forma de intercambio de redes que se habla mucho.

La receta de Shannon es la siguiente:

¿Qué harías si una acción subiera de 1 a 2 y luego de 2 a 1?

Si estás dispuesto a invertir \(200, el secreto de Shannon es que compras acciones con \)100 y que tienes $100 en la bolsa, y lo único que tienes que hacer es mantener el valor de mercado de las acciones y el total de dinero en efectivo.

Por ejemplo, cuando 100 acciones ganan 200, tienes 200 acciones más 100 en efectivo, el total de los activos es de 300, entonces vendes 50 dólares por acción, por lo que tienes 150 acciones, 150 dólares en efectivo, y cuando las acciones caen un dólar, el valor de mercado de las acciones es de sólo 75, pero tu total de los activos es de 225!

Si las acciones bajan primero y luego vuelven a subir, y el resultado es el mismo, ¡todos ganan $25!

Esto no parece muy viable, las acciones subieron un par de veces, y la caída de un par de veces equivale a: 2 × 0.5-1 = 0, de todos modos, es un paso atrás, y la estrategia de Shannon de regresar al punto de partida realmente está ganando dinero.

El secreto de la fortuna de Shannon está en el uso de la fórmula de Kelly, el mayor tenedor del universo.

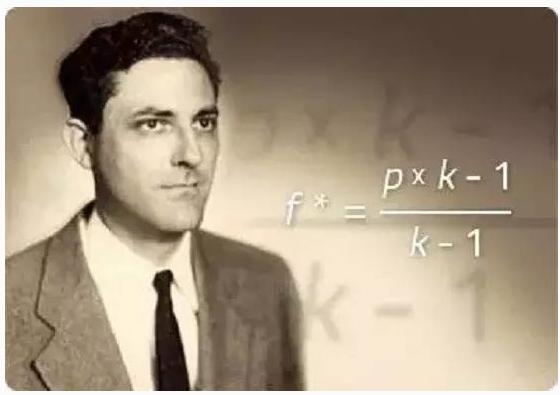
La fórmula fue citada por Kelly, un colega de Shannon en los Laboratorios Bell, para invertir en aplicaciones de procesamiento de señales de comunicación basadas en la informática de Shannon. La estrategia de Shannon mencionada anteriormente es utilizar esta fórmula.

La fórmula de Kelly es conocida en el mundo de las inversiones como la fórmula de la fortuna de las monedas, y trata sobre cómo calcular la proporción de inversión óptima en una apuesta o una inversión en función de la probabilidad de pérdidas.

La fórmula general de la ecuación de Kelly es la siguiente: f = (pb-q) / b

Por ejemplo, P es la probabilidad de que ganes dinero (por ejemplo, positivo), q es la probabilidad de que pierdas dinero, en el juego de lanzamiento de monedas, ambos valores son iguales a 0.5, b es tu probabilidad de ganar, es decir, cuánto dinero puedes ganar si pierdes el dinero.

Por ejemplo, cada vez que apuestas 1 pieza, el ganador te da 6 piezas, entonces este b es igual a 5 6 menos 1 pieza de tu dinero original, en este caso, el dinero que debes apostar cada vez es f = 5 × 0.5-0.5) / 5 = 40%, en este empate, cada vez que apuestes el 40% de tu dinero, tu rendimiento geométrico en el futuro será el máximo.

¡Ninguna proporción de inversión puede ser mejor que la fórmula de Kelly!

El principio de la fórmula de Kelly es realmente muy simple, para el valor total futuro de tu activo: C = (-1 + fb) ^ NP*(1-fa) ^ Nq (f: proporción de inversión, b probabilidad de ganar, a: probabilidad de perder, Np: número de ganancias, Nq: número de pérdidas), para C con f como variable de derivación, es decir, se obtiene la mejor f, la fórmula es: f = p/a-q/b

Esta fórmula es diferente a la anterior f = ((pb-q) / b, en realidad es la misma, si pierdes todo (por ejemplo, si lanzas una moneda al revés, cuando sale al revés, no tienes el dinero apostado) entonces a es igual a 0, y cuando a es igual a 0, es la misma fórmula anterior.

Utilizando la fórmula de Kelly para analizar el Diablo de Shannon, el aumento de la apuesta equivale a un doble, el ganador recibe dos monedas, y la disminución de la apuesta equivale a un doble, el ganador recibe cinco centavos. Utilizando la fórmula de Kelly para calcular la posición óptima del Diablo de Shannon, se puede utilizar la siguiente información: f = p/a-q/b = 0.⁵⁄₀.5-0.⁵⁄₁ = 0.5

Este es el secreto de los demonios de Shannon, la fórmula de Kelly calcula que la mejor proporción de inversión es invertir la mitad del capital, por lo que el principio detrás de cada vez que Shannon necesita ajustar el valor de mercado es el mismo.

¿Cuánto dinero ganaría Shannon si siguiera con esta estrategia?

El proceso derivado de la fórmula de Kelley descrito anteriormente es el siguiente: C = 1 + 0,5 × 1) ^ Np*(1-0.5 × 0.5) ^ Nq, suponiendo que la probabilidad de subida y bajada es igual a largo plazo, Np = Nq = n, el resultado es:

En otras palabras, los activos de Shannon se incrementarán en la n-ésima potencia de 1.125, ¿no suena esto como una ganancia excesiva y terrible?

Pero eso es contrario a la intuición, ¿no?

¿El que sube y baja, cae y sube, vuelve y vuelve, pisa el suelo, cambia el dinero?

Si estudiamos más detenidamente, encontraremos una brecha, invertir un dólar en el momento de la ganancia, pero invertir un dólar en el momento de la caída, sólo perderá 0.5, de acuerdo con la probabilidad de la expectativa de cálculo: 1 × 0.5-0.5 × 0.5 = 0.25, esta paradoja es evidente que hay una expectativa de ganancia positiva.

Pero si es un juego que existe con expectativas positivas de ganancias, ¿por qué si tienes todo el depósito, al final queda vacío y no ganas nada?

Es un fenómeno muy interesante, ¡y su rentabilidad final tiene una relación muy importante con su porcentaje de posesión!

El error en la posición es que en un juego con expectativas positivas de ganancias, aún puedes no ganar nada.

Si usamos el concepto de ganancias para medir el demonio de Shannon y descubrimos que la ganancia es: 2 × 0.5 = 1 (2: doblar, 0.5: contraposición), entonces nunca habrá ganancias en un juego, y nunca habrá ganancias.

La fórmula de Kelly es una fórmula mágica que puede hacer que la rentabilidad geométrica sea cero, pero que crea una riqueza infinita.

Si pensamos más en el demonio de Shannon, podríamos pensar que el alza y la caída se reducen a cero y que aún se puede ganar dinero, lo cual no es científico, el problema es que el alza de un dólar y la caída son solo 0.5.

En realidad, tal vez sea la ilusión causada por la desigualdad de probabilidades, la probabilidad de doblarse es probablemente menor que la de caer a la mitad, por lo que la probabilidad de la fórmula anterior debe modificarse y no se puede ganar dinero.

Y el demonio de Shannon sugiere que las probabilidades son iguales. ¿No es absurdo pensar que es razonable, que las probabilidades son diferentes, o que el dinero sale de la nada?

Así que ahora vamos a ver si es la misma cosa que tener la probabilidad de subir 1 y la de bajar 1 y la de bajar 1 y la de bajar 1 y la de bajar 1 y la de bajar 1 y la de bajar 1 y la de bajar 1 y la de bajar 1 y la de bajar 1 y la de bajar 1 y la de bajar 1 y la de bajar 1 y la de bajar 1 y la de bajar 1 y la de bajar 1 y la de bajar 1 y la de bajar 1 y la de bajar 1 y la de bajar 1 y la de bajar 1 y la de bajar 1 y la de bajar 1 y la de bajar 1 y la de bajar 1 y la de bajar 1 y la de bajar 1 y la de bajar 1 y la de bajar 2.

Uno sube 100 por ciento, otro baja 50 por ciento, parece totalmente diferente, obviamente el aumento del 100 por ciento es menor que el descenso del 50 por ciento.

El 100% y el 50% son solo una amplitud, no una probabilidad, en cuanto a la rentabilidad de la bolsa de valores, la académica y la práctica adoptan la rentabilidad logarítmica, aunque la práctica muestra que la rentabilidad logarítmica no se ajusta perfectamente a la distribución normal, pero después de todo la proximidad es muy alta.

Hasta que no haya un modelo mejor, podríamos analizar el rendimiento binario de una distribución normal y ver la respuesta: ¡La probabilidad de un aumento del 100% y una disminución del 50% en la distribución de la rentabilidad congruente es la misma!

En una situación de igualdad de probabilidades, con un rendimiento a largo plazo de cero, se puede ganar dinero con el diablo de Shannon, ¡no es tan fuerte!

Entonces, ¿cuánto dinero se puede ganar con 50 efectivo y 50 posiciones?

Para calcular el 10% más arriba, el rendimiento logarítmico = ln ((1.1) = 0.09531, ahora vamos a calcular el rendimiento logarítmico de pares, cuál es el rendimiento aritmético: e ^ ((-0.0953) = 0.909 ▽ Es decir, la probabilidad de caída de lo que normalmente llamamos el 10% es: -9.09%, y tenemos la probabilidad de que (y es igual a 0.5), y tenemos la probabilidad de (y es igual a 10%, y es igual a 9.09%) ¿Qué podemos hacer?

Calculando la proporción óptima de tenencia con la fórmula de Kelly, y luego en el futuro sólo tendremos que comprar y vender algunas de las acciones de Shannon, mantener una proporción fija de tenencia, ¡y entonces podremos obtener las ganancias de Shannon!

De acuerdo con la fórmula de Kelly anterior: f = p/a-q/b, llevando en cuenta la probabilidad y la probabilidad que acabamos de calcular: f = 0.⁵⁄₀.0909-0.⁵⁄₀.1 = 5.5005-5 = 0.5005, es casi igual a 0.5。

Por lo tanto, el mejor porcentaje de tenencia calculado según la fórmula de Kelly es el cincuenta por ciento de la posición (si cambia el 10% al 30%, la tasa de tenencia cambia al 200%, el doble de la palanca).

En el proceso de deducción de la fórmula de Kelly que he mencionado anteriormente, he dicho:

C=（1+fb)^Np(1-fa) ^ Nq, y lo que estamos haciendo es asignar el número que acabamos de calcular: C=(1+0.5×0.1)(1-0.5×0.0909)^n=(1.05×0.95455)^n=1.0022^n

Diseñado de acuerdo con la fórmula de Kelly de la proporción de inversión perfecta, una máquina que realiza operaciones perfectas en el espacio de la oscilación del 19,09%, puede obtener un beneficio neto del 0,22% en el mercado por cada operación, sin contar el costo de la transacción, con la premisa de una distribución normal de la rentabilidad lineal en el mercado de valores.

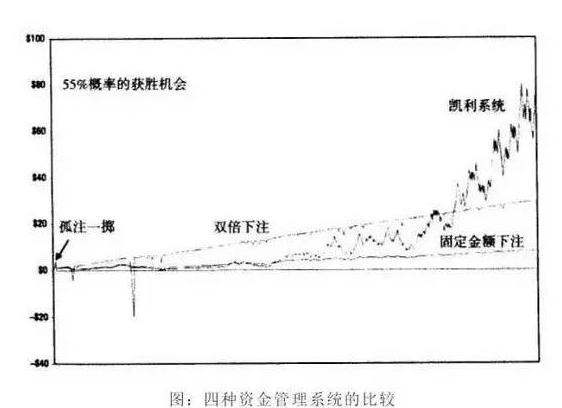
Dentro de las reglas, esta tasa de ganancias es la más rápida de crecimiento de capital en la cuenta, que es el principio fundamental de la gestión de posiciones para estabilizar la ganancia en caso de que la expectativa de la red sea de 0.

En resumen, el método de negociación de la red es un buen método de negociación, pero también tiene algunas desventajas, es decir, la posibilidad de que las reglas no funcionen, como el temor a la ruptura de la red, el temor a la unilateralidad, etc.

En el blog de la red social, se puede encontrar información sobre las transacciones de la red: https://www.fmz.cn/bbs-topic/7567 Las reglas de comercio de la ley de comercio de la red se detallan Los principios científicos de la estabilidad de las ganancias https://www.fmz.cn/bbs-topic/7568 Las ventajas y desventajas de las transacciones en red y cómo optimizar las estrategias https://www.fmz.cn/bbs-topic/7569 Optimización de la estrategia de la ley de comercio de la red: cómo elegir la variedad de inversión adecuada https://www.fmz.cn/bbs-topic/7570 Optimización de la estrategia de la ley de transacciones de la red: solucionar el problema de la caída unilateral y reducir la tasa de ruptura de la red https://www.fmz.cn/bbs-topic/7571 Optimización de la estrategia de la ley de comercio de la rejilla - Cómo usar la gestión de posiciones para resolver rápidamente https://www.fmz.cn/bbs-topic/7572 Optimización final de la ley de comercio de la red: las ganancias de la red también se multiplican por 5 https://www.fmz.cn/bbs-topic/7524 Una estrategia de red para modificar la estrategia de la tarjeta de alta frecuencia