La semana pasada, presentamosGestión del riesgo VaRCuando hablamos del riesgo de una cartera, no es igual al riesgo de cada activo individual, sino que está relacionado con su correlación de precios. Si tomamos dos activos como ejemplo, si su correlación positiva es muy fuerte, es decir, suben y bajan al mismo tiempo, entonces la diversificación de las inversiones a largo plazo no reducirá el riesgo. Si la correlación negativa es muy fuerte, la diversificación puede reducir significativamente el riesgo. La pregunta natural es: al invertir en una cartera, ¿cómo maximizar el rendimiento con un determinado nivel de riesgo? Aquí es donde entra en juego la teoría de Markowitz, que presentaré hoy.

La Teoría Moderna de Carteras (MPT), propuesta por Harry Markowitz en 1952, es un marco matemático para la selección de carteras que tiene como objetivo maximizar los rendimientos esperados mediante la selección de diferentes combinaciones de activos riesgosos. La idea central es que los precios de los activos no se mueven en perfecta sincronía (es decir, existe una correlación imperfecta entre los activos) y el riesgo general de la inversión se puede reducir diversificando la asignación de activos.

Conceptos clave de la teoría de Markowitz

1. Tasa de rendimiento esperada:Es el rendimiento que un inversor puede esperar obtener al mantener un activo o una cartera, generalmente previsto en función de datos de rendimiento históricos.

\(E(R_p) = \sum_{i=1}^{n} w_i E(R_i)\)

Donde \(E(R_p)\) es la tasa de rendimiento esperada de la cartera, \(wi\) es el peso del \(i\)ésimo activo en la cartera y \(E(R_i)\) es la tasa de rendimiento esperada del \( i\)ésimo activo. .

1. Riesgo (volatilidad o desviación estándar):Se utiliza para medir la incertidumbre del rendimiento de una inversión o la volatilidad de una inversión.

\(\sigma_p = \sqrt{\sum_{i=1}^{n} \sum_{j=1}^{n} w_i w_j \sigma_{ij}}\)

Donde \(\sigma_p\) es el riesgo total de la cartera y \(\sigma_{ij}\) es la covarianza entre el activo \(i\) y el activo \(j\), que mide la relación entre los cambios de precios de los dos activos.

1. Covarianza:Mide la correlación entre los movimientos de precios de dos activos.

\(\sigma_{ij} = \rho_{ij} \sigma_i \sigma_j\)

Donde \(\rho_{ij}\) es el coeficiente de correlación entre el activo \(i\) y el activo \(j\), \(\sigma_i\) y \(\sigma_j\) son las desviaciones estándar del activo \(i\) y el activo \(j\) respectivamente.

1. Frontera eficiente:En el sistema de coordenadas riesgo-rendimiento, la frontera eficiente es el conjunto de carteras que pueden proporcionar el máximo rendimiento esperado a un nivel de riesgo dado.

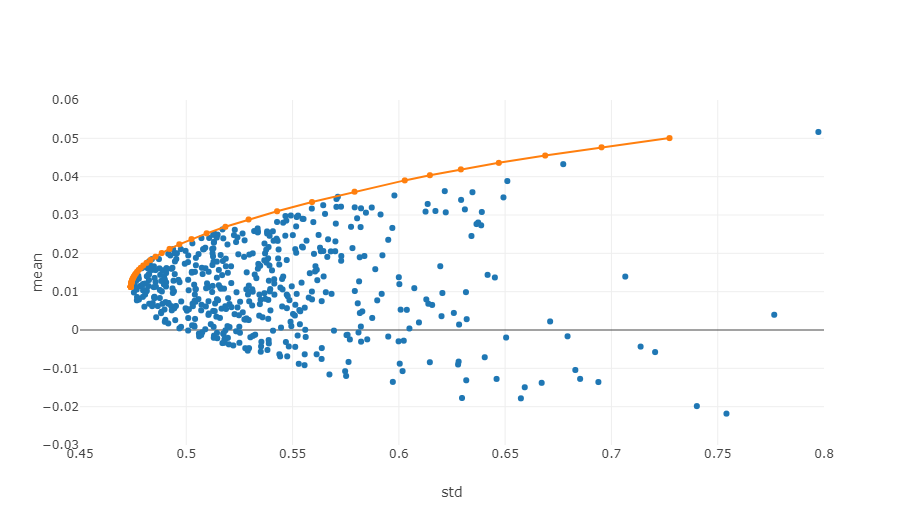
La imagen anterior es un diagrama esquemático de la frontera efectiva. Cada punto representa una cartera de inversiones con diferentes ponderaciones. El eje horizontal es la volatilidad, es decir, el nivel de riesgo, y el eje vertical es la tasa de retorno. Obviamente, nos centramos en el borde superior del gráfico, que consigue el mayor rendimiento con el mismo nivel de riesgo.

En el comercio cuantitativo y la gestión de carteras, la aplicación de estos principios requiere el análisis estadístico de datos históricos y el uso de modelos matemáticos para estimar los rendimientos esperados, las desviaciones estándar y las covarianzas de varios activos. Luego, se aplican técnicas de optimización para encontrar la mejor configuración del peso de los activos. Este proceso generalmente implica cálculos matemáticos complejos y mucho procesamiento informático, por lo que el análisis cuantitativo se ha vuelto muy importante en las finanzas modernas. A continuación, se utilizará un ejemplo específico de Python para ilustrar cómo optimizar.

Ejemplo de código Python para encontrar la combinación óptima mediante el método de simulación

El cálculo de la cartera óptima de Markowitz es un proceso de varios pasos que implica varios pasos clave, como la preparación de datos, la simulación de la cartera y el cálculo de indicadores. Referencia: https://plotly.com/python/v3/ipython-notebooks/markowitz-portfolio-optimization/

1. Obtener datos del mercado：

   • aprobarget_dataFunción para obtener los datos de precios históricos de la moneda digital seleccionada. Estos son los datos necesarios para calcular la tasa de rendimiento y el riesgo, que se utilizan para construir carteras y calcular el ratio de Sharpe.

2. Cálculo de rentabilidad y riesgo：

   • usarcalculate_returns_riskLa función calcula la tasa de rendimiento anualizada y el riesgo anualizado (desviación estándar) para cada moneda digital. Esto es para cuantificar el rendimiento histórico de cada activo para su uso en una cartera óptima.

3. Calcular la cartera óptima de Markowitz：

   • usarcalculate_optimal_portfolioFunción que simula múltiples carteras. En cada simulación, los pesos de los activos se generan aleatoriamente y luego se calculan el rendimiento esperado y el riesgo de la cartera en función de estos pesos.
   • Al generar aleatoriamente combinaciones de diferentes pesos, se pueden explorar múltiples carteras posibles para encontrar la mejor combinación. Esta es una de las ideas centrales de la teoría de cartera de Markowitz.

El objetivo de todo el proceso es encontrar la cartera que ofrezca el mejor rendimiento esperado para un nivel de riesgo determinado. Al simular múltiples combinaciones posibles, los inversores pueden comprender mejor cómo se comportarían las diferentes configuraciones y elegir la combinación que mejor se adapte a sus objetivos de inversión y tolerancia al riesgo. Este enfoque ayuda a optimizar las decisiones de inversión y hacer que las inversiones sean más eficientes.

import numpy as np
import pandas as pd
import requests
import matplotlib.pyplot as plt

# 获取行情数据
def get_data(symbols):
    data = []
    for symbol in symbols:
        url = 'https://api.binance.com/api/v3/klines?symbol=%s&interval=%s&limit=1000'%(symbol,'1d')
        res = requests.get(url)
        data.append([float(line[4]) for line in res.json()])
    return data

def calculate_returns_risk(data):
    returns = []
    risks = []

    for d in data:
        daily_returns = np.diff(d) / d[:-1]
        annualized_return = np.mean(daily_returns) * 365
        annualized_volatility = np.std(daily_returns) * np.sqrt(365)

        returns.append(annualized_return)
        risks.append(annualized_volatility)

    return np.array(returns), np.array(risks)

# 计算马科维茨最优组合
def calculate_optimal_portfolio(returns, risks):
    n_assets = len(returns)
    num_portfolios = 3000

    results = np.zeros((4, num_portfolios), dtype=object) 


    for i in range(num_portfolios):
        weights = np.random.random(n_assets)
        weights /= np.sum(weights)

        portfolio_return = np.sum(returns * weights)
        portfolio_risk = np.sqrt(np.dot(weights.T, np.dot(np.cov(returns, rowvar=False), weights)))

        results[0, i] = portfolio_return
        results[1, i] = portfolio_risk
        results[2, i] = portfolio_return / portfolio_risk
        results[3, i] = list(weights) # 将权重转换为列表

    return results

symbols = ['BTCUSDT','ETHUSDT', 'BNBUSDT','LINKUSDT','BCHUSDT','LTCUSDT']
data = get_data(symbols)

returns, risks = calculate_returns_risk(data)
optimal_portfolios = calculate_optimal_portfolio(returns, risks)

max_sharpe_idx = np.argmax(optimal_portfolios[2])
optimal_return = optimal_portfolios[0, max_sharpe_idx]
optimal_risk = optimal_portfolios[1, max_sharpe_idx]
optimal_weights = optimal_portfolios[3, max_sharpe_idx]

# 输出结果
print("最优组合:")
for i in range(len(symbols)):
    print(f"{symbols[i]}权重: {optimal_weights[i]:.4f}")

print(f"预期收益率: {optimal_return:.4f}")
print(f"预期风险(标准差): {optimal_risk:.4f}")
print(f"夏普比率: {optimal_return / optimal_risk:.4f}")

# 可视化投资组合
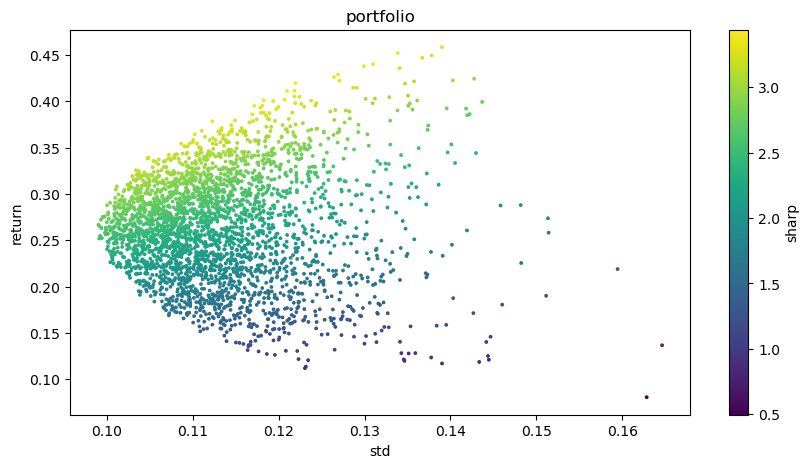
plt.figure(figsize=(10, 5))
plt.scatter(optimal_portfolios[1], optimal_portfolios[0], c=optimal_portfolios[2], marker='o', s=3)
plt.title('portfolio')
plt.xlabel('std')
plt.ylabel('return')
plt.colorbar(label='sharp')
plt.show()

Resultado final: La mejor combinación: Peso de BTCUSDT: 0,0721 Peso de ETHUSDT: 0,2704 Peso de BNBUSDT: 0,3646 Peso de LINKUSDT: 0,1892 Peso del BCHUSDT: 0,0829 Peso de LTCUSDT: 0,0209 Tasa de rendimiento esperada: 0,4195 Riesgo esperado (desviación estándar): 0,1219 Relación de Sharpe: 3,4403