La estadística bayesiana es una poderosa disciplina en matemáticas con amplias aplicaciones en muchos campos, incluidas las finanzas, la investigación médica y la tecnología de la información. Nos permite combinar creencias previas con evidencia para llegar a nuevas creencias posteriores, permitiéndonos tomar decisiones más informadas.

En este artículo presentaremos brevemente algunos de los principales matemáticos que fundaron este campo.

Antes de Bayes Para comprender mejor las estadísticas bayesianas, debemos remontarnos al siglo XVIII y referirnos al matemático De Moivre y su artículo “El principio del azar”.[1]。

En su tratado, De Moivre abordó muchos de los problemas de su tiempo relacionados con la probabilidad y el juego. Como probablemente sabes, su solución a uno de estos problemas condujo al origen de la distribución normal, pero esa es otra historia.

En su artículo hay una pregunta sencilla:

“La probabilidad de obtener tres caras al lanzar una moneda justa tres veces seguidas”.

Al leer los problemas descritos en “El principio del azar”, se puede observar que la mayoría de ellos comienzan con una hipótesis a partir de la cual se calcula la probabilidad de un evento dado. Por ejemplo, en el problema anterior, se supone que la moneda es justa, por lo que la probabilidad de obtener cara en un lanzamiento es 0,5.

Hoy en día esto se expresa en términos matemáticos como:

𝑃(𝑋|𝜃)

¿Pero qué pasa si no sabemos si la moneda es justa? Si no lo sabemos𝜃¿Paño de lana?

Thomas Bayes y Richard Price

Casi cincuenta años después, en 1763, se publicó un artículo titulado “Un ensayo sobre el principio del azar”.[2] Publicado en las Philosophical Transactions de la Royal Society de Londres.

En las primeras páginas del documento hay un texto escrito por el matemático Richard Price, que resume el contenido de un artículo escrito por su amigo Thomas Bayes unos años antes de su muerte. En la introducción, Price explica la importancia de algunos descubrimientos realizados por Thomas Bayes que no fueron cubiertos en los Principios del Azar de De Moivre.

De hecho, se refería a un problema específico:

“Dado el número de ocurrencias y fallas de un evento desconocido, encuentre la probabilidad de que su ocurrencia esté entre dos grados de probabilidad nombrados.”

En otras palabras, después de observar un evento, encontramos el parámetro desconocido.θ¿Cuál es la probabilidad entre dos grados de probabilidad? Este es en realidad uno de los primeros problemas de la historia relacionados con la inferencia estadística y dio origen al nombre de probabilidad inversa. En términos matemáticos:

𝑃( 𝜃 | 𝑋）

Esto es, por supuesto, lo que hoy llamamos la distribución posterior del teorema de Bayes.

Causas sin causa

Conozca a estos dos pastores ancianos.Thomas BayesyPrecio de RichardLo que motivó la investigación es realmente muy interesante. Pero para hacer esto, necesitamos dejar de lado por un momento algunos conocimientos sobre estadística.

Estamos en el siglo XVIII y la probabilidad se está convirtiendo en un área de creciente interés para los matemáticos. Matemáticos como De Moivre o Bernoulli habían demostrado que algunos acontecimientos ocurren con cierto grado de aleatoriedad pero aún así están regidos por reglas fijas. Por ejemplo, si lanzas un dado muchas veces, una de cada seis veces caerá en un seis. Es como si hubiera una regla oculta que determina el destino del azar.

Ahora, imagina que eres un matemático y un devoto creyente que vive en este período. Quizás te interese saber cómo se relaciona esta regla oculta con Dios.

Ésta es de hecho la pregunta que se plantearon los propios Bayes y Price. La solución que esperaban resolver a este problema era directamente aplicable a demostrar que “el mundo debe ser el resultado de la sabiduría y la inteligencia; proporcionando así evidencia de la existencia de Dios como causa final”.[2] - Es decir, no hay causa y efecto.

Laplace

Sorprendentemente, unos dos años después, en 1774, aparentemente sin haber leído el artículo de Thomas Bayes, el matemático francés Laplace escribió un artículo titulado “Sobre las causas de los acontecimientos a través de las probabilidades de los acontecimientos”.[3], que es un artículo sobre el problema de probabilidad inversa. En la primera página puedes leer

Los principios fundamentales son:

“Si un evento puede ser causado por n causas diferentes, entonces las probabilidades de estas causas para un evento dado están en una razón igual a la probabilidad del evento dada la causa, y la probabilidad de la existencia de cada una de estas causas es igual “a la probabilidad del evento dada la causa. La probabilidad de las causas, dividida por la suma de las probabilidades del evento dada cada una de esas causas”.

Esto es lo que hoy conocemos como teorema de Bayes:

​

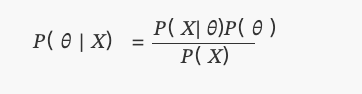
enP(θ)se distribuye uniformemente.

Experimento con monedas

Traeremos las estadísticas bayesianas al presente utilizando Python y la biblioteca PyMC y realizando un experimento simple.

Imagina que un amigo te da una moneda y te pregunta si crees que es una moneda justa. Como tiene prisa, te dice que sólo lances la moneda 10 veces. Como puedes ver, hay un parámetro desconocido en este problema.p, la probabilidad de obtener cara en el lanzamiento de una moneda, y queremos estimar estopEl valor más probable de .

(Nota: No estamos hablando de parámetrospes una variable aleatoria, pero este parámetro es fijo y queremos saber entre qué valores es más probable que esté. ）

Para tener una perspectiva diferente sobre este problema, lo abordaremos bajo dos creencias previas diferentes:

• 1. No tienes información previa sobre la imparcialidad de la moneda y asignas probabilidades iguales ap. En este caso, utilizaremos lo que se llama una hipótesis no informativa, porque no estás añadiendo ninguna información a tu creencia.
• 1. Sabes por experiencia que, aunque una moneda pueda ser injusta, es difícil hacerla muy injusta, por lo que crees que los parámetrospLo más probable es que no baje de 0,3 ni supere 0,7. En este caso utilizaremos un prior informativo.

Para ambos casos, nuestras creencias previas serán las siguientes:

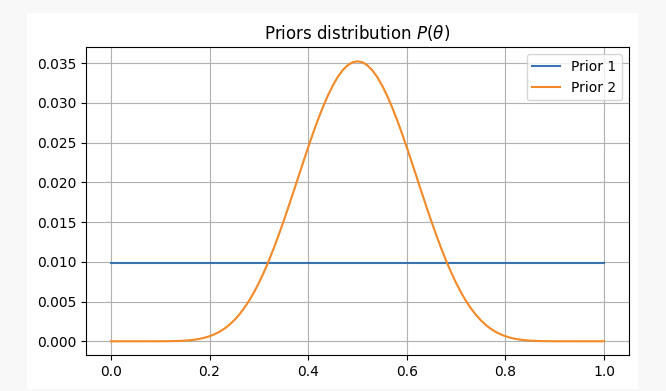
Después de lanzar una moneda 10 veces, obtienes 2 caras. Con esta evidencia, probablemente podamos averiguar dónde encontrar nuestros parámetros.p？

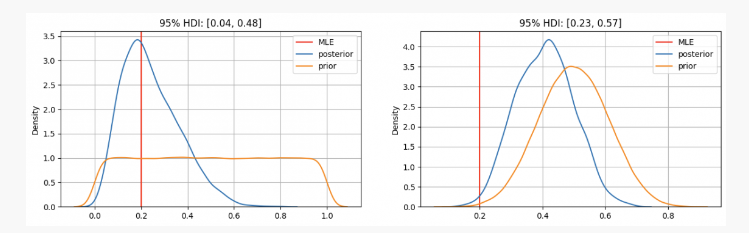
Como puedes ver, en el primer caso tenemospLa distribución previa de se centra en la estimación de máxima verosimilitud (MLE)p=0.2, que es un enfoque similar que utiliza el método frecuentista. El verdadero parámetro desconocido estará dentro del intervalo de credibilidad del 95% entre 0,04 y 0,48.

Por otra parte, cuando hay una alta confianza en que el parámetrop Si bien debería estar entre 0,3 y 0,7, podemos ver que la distribución posterior está alrededor de 0,4, que es mucho más alto que el valor dado por nuestro MLE. En este caso, el verdadero parámetro desconocido estará dentro del intervalo de credibilidad del 95% entre 0,23 y 0,57.

Entonces, en el primer caso, le dirías a tu amigo que estás seguro de que la moneda es injusta. Pero en otro caso, le dirías que no estás seguro de si la moneda es justa.

Como puede verse, incluso con la misma evidencia (2 caras de 10 lanzamientos), los resultados pueden ser diferentes dadas diferentes creencias previas. Esta es una fortaleza de la estadística bayesiana, que, de manera similar al método científico, nos permite actualizar nuestras creencias combinando creencias previas con nuevas observaciones y evidencia.

END

En el artículo de hoy vimos los orígenes de la estadística bayesiana y sus principales contribuyentes. Desde entonces, ha habido muchos otros contribuyentes importantes a este campo de la estadística (Jeffreys, Cox, Shannon, etc.), reproducidos desde quantdare.com.