Poireaux et spread bid-ask : une étude préliminaire sur le modèle EKOP

• #### 1 Première partie

Ces derniers temps, j’ai été extrêmement occupé, et cela fait des mois depuis la dernière fois que j’ai écrit un article. De nombreuses choses se sont produites ces derniers mois, dont certaines ont été des nuages noirs pour ma propre vie. Mais ces expériences m’ont montré que la vie, comme le commerce, est pleine d’incertitudes et de hauts et de bas. Nous espérons toujours pouvoir apprendre quelque chose de ce qui s’est passé et nous approcher lentement de la vérité qui n’existe peut-être pas.

Nous savons tous qu’une action activement négociée a généralement un écart d’achat et de vente relativement faible, tandis qu’une action non activement négociée a le contraire. Pourquoi cela se produit-il? Peut-on expliquer l’écart de prix avec un modèle mathématique simple et beau?[1] Le but initial de cette étude était de déterminer si le comportement des traders ayant des informations différentes était à l’origine de la différence entre les deux catégories de prix. Dans ce billet, j’expliquerai les bases de ce modèle. L’application du modèle sera analysée plus en détail dans les articles suivants (si j’en ai le temps).

• #### 2 Les hypothèses du processus de transaction

Quand nous parlons d’un modèle financier, le plus important est de faire attention aux hypothèses de ce modèle. Un bon modèle financier a ses propres hypothèses: il ne sera pas trop fort pour ne pas être universel; il ne sera pas trop faible pour ne pas déduire de résultats beaux et concis. Les hypothèses de base du modèle EKOP sont les suivantes:

Hypothèse 1: nous parlons d’une transaction d’actions dont l’activité est dispersée dans la journée et continue dans la journée. C’est-à-dire que les transactions des traders ont lieu sur 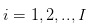de ces jours de transaction dispersés.

• Les mauvaises nouvelles, nous avons noté la valeur des actions comme
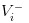
• Une bonne nouvelle est arrivée, nous avons enregistré la valeur de l’action comme
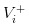
• Il n’y a pas de nouvelles, nous avons enregistré la valeur des actions comme

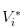
Il est clair que nous avons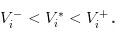

Hypothèse 2: il y a un jour où il y a un alpha.

La probabilité d’un événement ayant une incidence sur le prix d’une action est de 1 -α pour un événement n’ayant pas d’incidence sur le prix de l’action. Les jours où l’événement se produit, il y a une probabilité de 1 -δ pour un événement mauvais qui fait baisser le prix de l’action, et une probabilité de 1 -δ pour un événement bon qui fait monter le prix de l’action.

Hypothèse 3: Les participants à la négociation d’actions sont des market makers, des traders informés et des traders non informés. Ils se comportent respectivement comme suit:

MM est toujours prêt à placer un ordre d’achat ou de vente d’une unité à tout moment, comme c’est son devoir en tant que commerçant. MM est neutre en termes de risque, donc le prix qu’il place est celui qu’il considère comme juste.

IT ne négocie que les jours où il y a des nouvelles, leur comportement de négociation est un processus de repos. Un jour, s’il y a de mauvaises nouvelles, il mettra un ordre de vente à un taux d’arrivée de μ; et les jours où il y a de bonnes nouvelles, il mettra un ordre d’achat à un taux d’arrivée de μ.

UT, c’est-à-dire notre pauvre salade, avec l’avantage de l’absence de nouvelles, leur comportement de négociation est aussi un processus de repos, chaque jour, avec un taux d’arrivée pour les achats et les ventes. Notez que tous les processus de Poisson sont indépendants les uns des autres. Nous pouvons représenter l’hypothèse 3 avec un diagramme, comme suit:

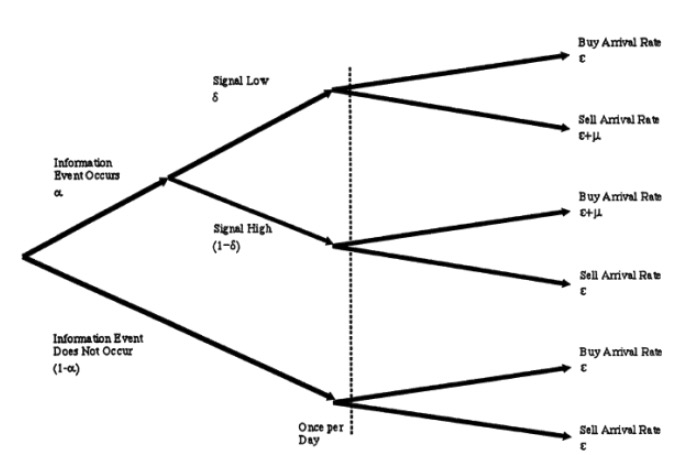
• #### 3 Mise à jour des transactions et des prix

Nous savons que les marketeurs sont généralement des gens qui travaillent pour les grandes entreprises. Ils sont très intelligents et ont résumé tous les paramètres du modèle dans le diagramme de l’arbre ci-dessus grâce à une grande quantité d’analyse de données historiques. Heureusement, ils ne sont pas aussi bien informés que les traders, qui ne savent pas si quelque chose d’important s’est passé aujourd’hui quand une journée de négociation est sur le point de commencer.

Maintenant, essayons de jouer le rôle d’un MM et de nous battre contre les TI et les UT. À un moment donné, nous nous sommes inscrits comme un vecteur sur la probabilité que quelque chose se produise, que quelque chose soit bon ou mauvais.

Il est évident qu’au début de la journée, c’est-à-dire au moment de la sortie de /upload/asset/7a5565722b92d2accf331f58923d6bab702659de.png, je n’avais pas vu de bulletin, donc tout ce que je pouvais faire était de supposer que la probabilité que rien ne se produise était α, la probabilité que quelque chose de bien se produise était /upload/asset/c9cf50c6146a25c662c593ed229845822bfac7a5.png, et la probabilité que quelque chose de mal se produise était /upload/asset/87418f07b12fce65f4c3f70b24b0e94d2e19f769a.png.

Comment mettre à jour cette probabilité ? Eh bien, nous qui faisons des choix commerciaux, nous connaissons la formule de Bayes. Lorsque nous observons une vente, nous utilisons la loi de Bayes pour mettre à jour notre propre estimation de probabilité.

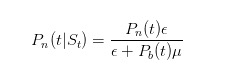
La molécule de cette formule dit que seul le trader ignorant vendra sous ε quand il n’y aura pas de nouvelles; et le décimal dit que le trader ignorant vendra sous ε à tout moment, et le trader informé vendra sous μ seulement quand il y aura des mauvaises nouvelles.

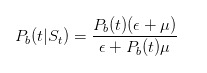
et

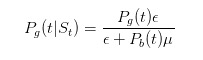
Avant de poursuivre avec cette déduction, nous allons faire quelques tests simples. Nous avons dit que si nous voyons un billet de vente, nous devrions augmenter notre estimation de la probabilité que quelque chose de mal se produise.

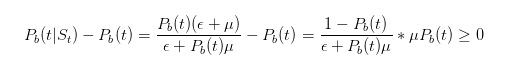
Il est donc évident que notre déduction confirme notre intuition.

Avec la probabilité actualisée, nous pouvons calculer le juste prix comme le prix d’achat que nous faisons sur le marché.

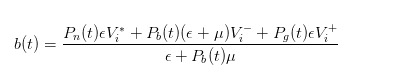
Par une déduction similaire, nous pouvons voir que lorsque l’ordre d’achat est envoyé, le prix de vente que nous avons déclaré en tant que vendeur devrait être

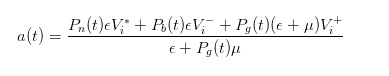
• #### 4 Expression de la différence de prix après transformation du prix

Si l’expression de prix d’achat et de vente ci-dessus n’est pas assez intuitive, nous pouvons introduire la valeur attendue de l’action au moment t pour simplifier l’expression. Nous avons une valeur attendue de

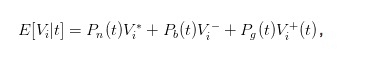
Nous pouvons donc transformer les expressions bid et ask en

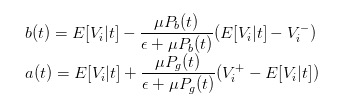
Nous pouvons donc clairement exprimer la différence de prix comme

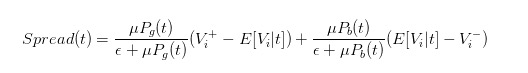
• #### 5 Les effets du comportement des commerçants sur la différence de prix

Avec l’expression de la différence de prix, nous pouvons analyser l’impact des différents commerçants sur la différence de prix !

Le plus d’épinards, le moins d’écart. Remarquez que ε est le taux d’arrivée des traders ignorants (nous les appellerons simplement épinards), et si ε >> μ, nous pouvons trouver, / upload/asset/539e0cfb1aae368277dd0e3840448b6a39abd087.png Les deux éléments vont vers 0, ce qui signifie que le spread va aussi vers zéro. Si nous allons à l’autre extrême, en supposant qu’il n’y ait plus de colza sur le marché et qu’il n’y ait qu’un groupe de commerçants bien informés, nous découvrirons malheureusement que les prix que nous affichons seront 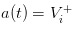et /upload/asset/1248ca7d3d472490982c9d0aa7b2e04b51269b18.png, de sorte que les commerçants bien informés se rendront compte que la vente et l’achat ne seront pas rentables et que le marché s’effondrera inévitablement.

C’est peut-être ce qui fait le charme des modèles mathématiques que nous puissions en tirer des conclusions si intéressantes et si profondes, en nous basant sur des hypothèses et en utilisant des déductions mathématiques très simples. Après avoir lu cet article, j’espère aussi que vous pourrez être gentils avec les épinards, car nous, les épinards, sommes la garantie que le marché peut fonctionner correctement !

[1] Easley, David, et al. “Liquidity, information, and infrequently traded stocks.” The Journal of Finance 51.4 (1996): 1405-1436.