La semaine dernière, nous avons présentéGestion des risques VaRLorsqu’on parle du risque d’un portefeuille, il n’est pas égal au risque de chaque actif individuel, mais est lié à leur corrélation de prix. Prenons l’exemple de deux actifs : si leur corrélation positive est très forte, c’est-à-dire qu’ils montent et descendent ensemble, la diversification des investissements à long terme ne réduira pas le risque. Si la corrélation négative est très forte, la diversification peut réduire considérablement le risque. La question naturelle est la suivante : lorsque l’on investit dans un portefeuille, comment maximiser les rendements à un certain niveau de risque ? C’est là qu’entre en jeu la théorie de Markowitz, que je vais présenter aujourd’hui.

La théorie moderne du portefeuille (MPT), proposée par Harry Markowitz en 1952, est un cadre mathématique pour la sélection de portefeuille qui vise à maximiser les rendements attendus en sélectionnant différentes combinaisons d’actifs risqués. profits tout en contrôlant les risques. L’idée principale est que les prix des actifs n’évoluent pas de manière parfaitement synchronisée (c’est-à-dire qu’il existe une corrélation imparfaite entre les actifs) et que le risque d’investissement global peut être réduit en diversifiant la répartition des actifs.

Concepts clés de la théorie de Markowitz

1. Taux de rendement attendu:Il s’agit du rendement qu’un investisseur peut espérer obtenir en détenant un actif ou un portefeuille, généralement prédit sur la base de données de rendement historiques.

\(E(R_p) = \sum_{i=1}^{n} w_i E(R_i)\)

Où \(E(R_p)\) est le taux de rendement attendu du portefeuille, \(wi\) est le poids du \(i\)ème actif du portefeuille et \(E(R_i)\) est le taux de rendement attendu du \( i\)ième actif. .

1. Risque (volatilité ou écart type):Utilisé pour mesurer l’incertitude du rendement d’un investissement ou la volatilité d’un investissement.

\(\sigma_p = \sqrt{\sum_{i=1}^{n} \sum_{j=1}^{n} w_i w_j \sigma_{ij}}\)

Où \(\sigma_p\) est le risque total du portefeuille et \(\sigma_{ij}\) est la covariance entre l’actif \(i\) et l’actif \(j\), qui mesure la relation entre les variations de prix des deux actifs.

1. Covariance:Mesure la corrélation entre les mouvements de prix de deux actifs.

\(\sigma_{ij} = \rho_{ij} \sigma_i \sigma_j\)

Où \(\rho_{ij}\) est le coefficient de corrélation entre l’actif \(i\) et l’actif \(j\), \(\sigma_i\) et \(\sigma_j\) sont les écarts types de l’actif \(i\) et de l’actif \(j\) respectivement.

1. Frontière efficace:Dans le système de coordonnées risque-rendement, la frontière efficiente est l’ensemble des portefeuilles qui peuvent fournir le rendement attendu maximal à un niveau de risque donné.

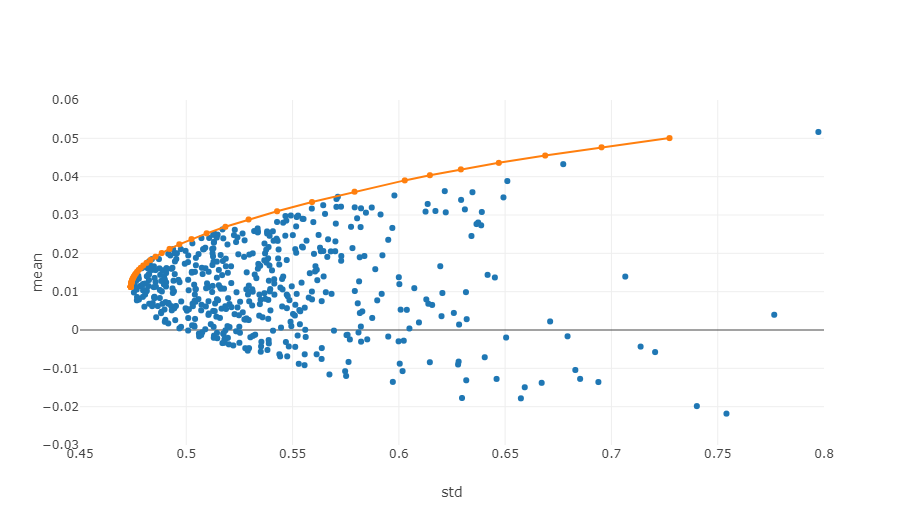
L’image ci-dessus est un diagramme schématique de la frontière effective. Chaque point représente un portefeuille d’investissement avec des pondérations différentes. L’axe horizontal représente la volatilité, c’est-à-dire le niveau de risque, et l’axe vertical le taux de rendement. Évidemment, nous nous concentrons sur le bord supérieur du graphique, qui génère le rendement le plus élevé au même niveau de risque.

Dans le trading quantitatif et la gestion de portefeuille, l’application de ces principes nécessite une analyse statistique des données historiques et l’utilisation de modèles mathématiques pour estimer les rendements attendus, les écarts types et les covariances de divers actifs. Ensuite, des techniques d’optimisation sont appliquées pour trouver la meilleure configuration de pondération des actifs. Ce processus implique généralement des calculs mathématiques complexes et beaucoup de traitement informatique, c’est pourquoi l’analyse quantitative est devenue très importante dans la finance moderne. Ce qui suit utilisera un exemple Python spécifique pour illustrer comment optimiser.

Exemple de code Python pour trouver la combinaison optimale à l’aide de la méthode de simulation

Le calcul du portefeuille optimal de Markowitz est un processus en plusieurs étapes impliquant plusieurs étapes clés telles que la préparation des données, la simulation de portefeuille et le calcul des indicateurs. Référence : https://plotly.com/python/v3/ipython-notebooks/markowitz-portfolio-optimization/

1. Obtenir des données de marché：

   • passerget_dataFonction permettant d’obtenir les données de prix historiques de la monnaie numérique sélectionnée. Il s’agit des données nécessaires au calcul du taux de rendement et du risque, qui sont utilisés pour construire des portefeuilles et calculer le ratio de Sharpe.

2. Calcul du rendement et du risque：

   • utilisercalculate_returns_riskLa fonction calcule le taux de rendement annualisé et le risque annualisé (écart type) pour chaque monnaie numérique. Il s’agit de quantifier la performance historique de chaque actif pour l’utiliser dans un portefeuille optimal.

3. Calculer le portefeuille optimal de Markowitz：

   • utilisercalculate_optimal_portfolioFonction, simulant plusieurs portefeuilles. Dans chaque simulation, les pondérations des actifs sont générées aléatoirement et le rendement et le risque attendus du portefeuille sont ensuite calculés sur la base de ces pondérations.
   • En générant aléatoirement des combinaisons de poids différents, plusieurs portefeuilles possibles peuvent être explorés pour trouver la meilleure combinaison. C’est l’une des idées fondamentales de la théorie du portefeuille de Markowitz.

L’objectif de l’ensemble du processus est de trouver le portefeuille qui offre le meilleur rendement attendu pour un niveau de risque donné. En simulant plusieurs combinaisons possibles, les investisseurs peuvent mieux comprendre les performances de différentes configurations et choisir la combinaison qui convient le mieux à leurs objectifs d’investissement et à leur tolérance au risque. Cette approche permet d’optimiser les décisions d’investissement et de rendre les investissements plus efficaces.

import numpy as np
import pandas as pd
import requests
import matplotlib.pyplot as plt

# 获取行情数据
def get_data(symbols):
    data = []
    for symbol in symbols:
        url = 'https://api.binance.com/api/v3/klines?symbol=%s&interval=%s&limit=1000'%(symbol,'1d')
        res = requests.get(url)
        data.append([float(line[4]) for line in res.json()])
    return data

def calculate_returns_risk(data):
    returns = []
    risks = []

    for d in data:
        daily_returns = np.diff(d) / d[:-1]
        annualized_return = np.mean(daily_returns) * 365
        annualized_volatility = np.std(daily_returns) * np.sqrt(365)

        returns.append(annualized_return)
        risks.append(annualized_volatility)

    return np.array(returns), np.array(risks)

# 计算马科维茨最优组合
def calculate_optimal_portfolio(returns, risks):
    n_assets = len(returns)
    num_portfolios = 3000

    results = np.zeros((4, num_portfolios), dtype=object) 


    for i in range(num_portfolios):
        weights = np.random.random(n_assets)
        weights /= np.sum(weights)

        portfolio_return = np.sum(returns * weights)
        portfolio_risk = np.sqrt(np.dot(weights.T, np.dot(np.cov(returns, rowvar=False), weights)))

        results[0, i] = portfolio_return
        results[1, i] = portfolio_risk
        results[2, i] = portfolio_return / portfolio_risk
        results[3, i] = list(weights) # 将权重转换为列表

    return results

symbols = ['BTCUSDT','ETHUSDT', 'BNBUSDT','LINKUSDT','BCHUSDT','LTCUSDT']
data = get_data(symbols)

returns, risks = calculate_returns_risk(data)
optimal_portfolios = calculate_optimal_portfolio(returns, risks)

max_sharpe_idx = np.argmax(optimal_portfolios[2])
optimal_return = optimal_portfolios[0, max_sharpe_idx]
optimal_risk = optimal_portfolios[1, max_sharpe_idx]
optimal_weights = optimal_portfolios[3, max_sharpe_idx]

# 输出结果
print("最优组合:")
for i in range(len(symbols)):
    print(f"{symbols[i]}权重: {optimal_weights[i]:.4f}")

print(f"预期收益率: {optimal_return:.4f}")
print(f"预期风险(标准差): {optimal_risk:.4f}")
print(f"夏普比率: {optimal_return / optimal_risk:.4f}")

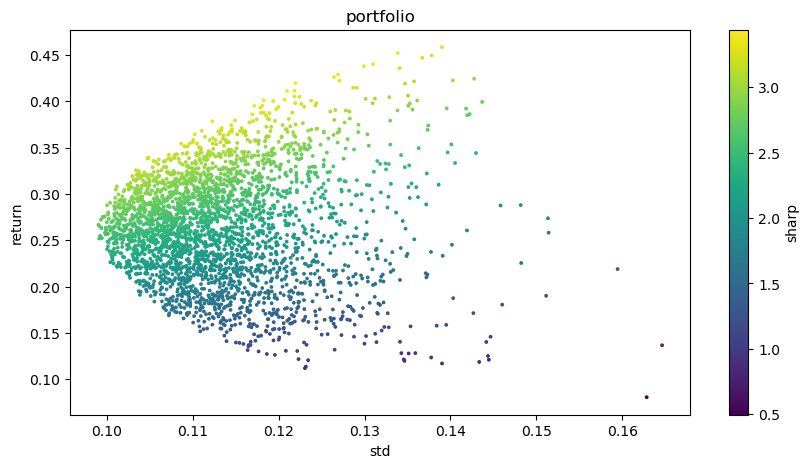
# 可视化投资组合
plt.figure(figsize=(10, 5))
plt.scatter(optimal_portfolios[1], optimal_portfolios[0], c=optimal_portfolios[2], marker='o', s=3)
plt.title('portfolio')
plt.xlabel('std')
plt.ylabel('return')
plt.colorbar(label='sharp')
plt.show()

Résultat final : Meilleure combinaison : Poids de BTCUSDT : 0,0721 Poids de la paire ETHUSDT : 0,2704 Poids du BNUSDT : 0,3646 Poids du LINKUSDT : 0,1892 Poids BCHUSDT : 0,0829 Poids LTCUSDT : 0,0209 Taux de rendement attendu : 0,4195 Risque attendu (écart type) : 0,1219 Ratio de Sharpe : 3,4403