La statistique bayésienne est une discipline puissante en mathématiques avec de larges applications dans de nombreux domaines, notamment la finance, la recherche médicale et les technologies de l’information. Cela nous permet de combiner des croyances antérieures avec des preuves pour arriver à de nouvelles croyances postérieures, nous permettant de prendre des décisions plus éclairées.

Dans cet article, nous présenterons brièvement certains des principaux mathématiciens qui ont fondé ce domaine.

Avant Bayes Pour mieux comprendre les statistiques bayésiennes, il faut remonter au 18e siècle et se référer au mathématicien De Moivre et à son article « Le principe de hasard »[1]。

Dans son traité, De Moivre aborde de nombreux problèmes de son époque liés aux probabilités et aux jeux de hasard. Comme vous le savez probablement, sa solution à l’un de ces problèmes a conduit à l’origine de la distribution normale, mais c’est une autre histoire.

Dans son article, il y a une question simple :

« La probabilité d’obtenir trois faces en lançant une pièce de monnaie trois fois de suite. »

En lisant les problèmes décrits dans « Le principe du hasard », vous remarquerez que la plupart d’entre eux commencent par une hypothèse à partir de laquelle la probabilité d’un événement donné est calculée. Par exemple, dans le problème ci-dessus, on suppose que la pièce est équitable, donc la probabilité d’obtenir un pile ou face dans un tirage au sort est de 0,5.

Cela s’exprime aujourd’hui en termes mathématiques comme suit :

𝑃(𝑋|𝜃)

Mais que se passe-t-il si nous ne savons pas si la pièce est équitable ? Si nous ne savons pas𝜃Étoffe de laine?

Thomas Bayes et Richard Price

Près de cinquante ans plus tard, en 1763, un article intitulé « Essai sur le principe du hasard »[2] Publié dans les Philosophical Transactions de la Royal Society de Londres.

Dans les premières pages du document, on trouve un texte écrit par le mathématicien Richard Price, résumant le contenu d’un article écrit par son ami Thomas Bayes quelques années avant sa mort. Dans l’introduction, Price explique l’importance de certaines découvertes faites par Thomas Bayes qui n’ont pas été abordées dans les Principes du hasard de De Moivre.

En fait, il faisait référence à un problème spécifique :

« Étant donné le nombre d’occurrences et d’échecs d’un événement inconnu, trouvez la probabilité que son occurrence se situe entre deux degrés de probabilité nommés. »

En d’autres termes, après avoir observé un événement, nous trouvons le paramètre inconnuθQuelle est la probabilité entre deux degrés de probabilité ? Il s’agit en fait de l’un des premiers problèmes de l’histoire lié à l’inférence statistique, et qui a donné naissance au nom de probabilité inverse. En termes mathématiques :

𝑃( 𝜃 | 𝑋）

C’est bien sûr ce que nous appelons aujourd’hui la distribution postérieure du théorème de Bayes.

Causes sans cause

Apprenez à connaître ces deux anciens pasteurs.Thomas BayesetRichard Price, ce qui a motivé la recherche est en fait très intéressant. Mais pour ce faire, nous devons mettre de côté un instant certaines connaissances en statistiques.

Nous sommes au 18e siècle et les probabilités deviennent un domaine d’intérêt croissant pour les mathématiciens. Des mathématiciens comme De Moivre ou Bernoulli ont montré que certains événements se produisent avec un certain degré de hasard mais sont néanmoins régis par des règles fixes. Par exemple, si vous lancez un dé plusieurs fois, une fois sur six, il tombera sur un six. C’est comme s’il y avait une règle cachée qui détermine le destin du hasard.

Maintenant, imaginez que vous êtes un mathématicien et un croyant fervent vivant à cette époque. Vous pourriez être intéressé de savoir comment cette règle cachée se rapporte à Dieu.

C’est en effet la question que Bayes et Price eux-mêmes se sont posée. La solution qu’ils espéraient pour résoudre ce problème était directement applicable à la preuve que « le monde doit être le résultat de la sagesse et de l’intelligence ; fournissant ainsi la preuve de l’existence de Dieu en tant que cause finale ».[2] - C’est-à-dire qu’il n’y a pas de cause à effet.

Laplace

Étonnamment, environ deux ans plus tard, en 1774, apparemment sans avoir lu l’article de Thomas Bayes, le mathématicien français Laplace a écrit un article intitulé « Sur les causes des événements à travers les probabilités des événements ».[3], qui est un article sur le problème de probabilité inverse. Sur la première page vous pouvez lire

Les principes fondamentaux sont les suivants :

« Si un événement peut être causé par n causes différentes, alors les probabilités de ces causes pour un événement donné sont dans un rapport égal à la probabilité de l’événement étant donné la cause, et la probabilité de l’existence de chacune de ces causes est égale « à la probabilité de l’événement étant donné la cause. La probabilité des causes, divisée par la somme des probabilités de l’événement étant donné chacune de ces causes. »

C’est ce que nous connaissons aujourd’hui sous le nom de théorème de Bayes :

​

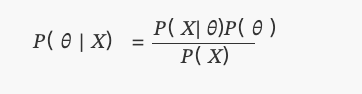
dansP(θ)est uniformément répartie.

Expérience avec des pièces de monnaie

Nous allons apporter les statistiques bayésiennes au présent en utilisant Python et la bibliothèque PyMC et en réalisant une expérience simple.

Supposons qu’un ami vous donne une pièce et vous demande si vous pensez que c’est une pièce équitable. Parce qu’il est pressé, il vous dit de ne lancer la pièce que 10 fois. Comme vous pouvez le voir, il y a un paramètre inconnu dans ce problèmep, la probabilité d’obtenir pile dans un tirage au sort, et nous voulons estimer celapLa valeur la plus probable de .

(Remarque : nous ne parlons pas de paramètrespc’est une variable aléatoire, mais ce paramètre est fixe et nous voulons savoir entre quelles valeurs il est le plus probable qu’il se situe. ）

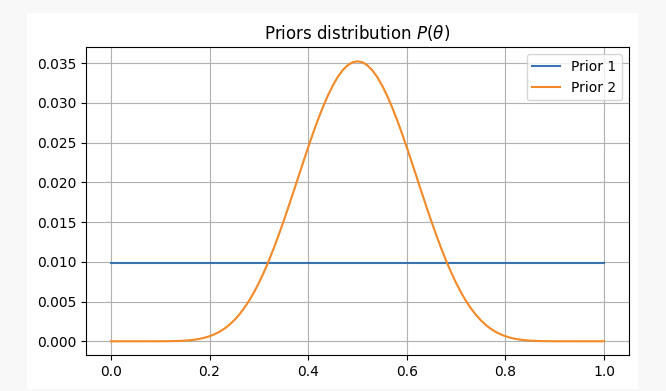
Pour avoir une perspective différente sur ce problème, nous l’aborderons sous deux croyances préalables différentes :

• 1. Vous n’avez aucune information préalable sur l’équité de la pièce et attribuez des probabilités égales àp. Dans ce cas, nous utiliserons ce qu’on appelle une priori non informative, car vous n’ajoutez aucune information à votre croyance.
• 1. Vous savez par expérience que même si une pièce peut être injuste, il est difficile de la rendre très injuste, vous pensez donc que les paramètrespIl est très probable que ce chiffre ne descende pas en dessous de 0,3 ni au-dessus de 0,7. Dans ce cas, nous utiliserons une priori informative.

Dans les deux cas, nos croyances préalables seront les suivantes :

Après avoir lancé une pièce 10 fois, vous obtenez 2 faces. Avec ces preuves, nous pouvons probablement déterminer où trouver nos paramètresp？

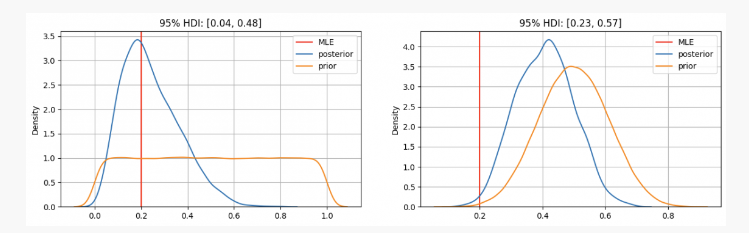
Comme vous pouvez le voir, dans le premier cas, nous avonspLa distribution a priori de est centrée sur l’estimation du maximum de vraisemblance (MLE)p=0.2, qui est une approche similaire utilisant la méthode fréquentiste. Le véritable paramètre inconnu se situera dans l’intervalle crédible à 95 % entre 0,04 et 0,48.

En revanche, lorsqu’il existe une grande confiance que le paramètrep Alors qu’elle devrait être comprise entre 0,3 et 0,7, on constate que la distribution postérieure est autour de 0,4, ce qui est bien supérieur à la valeur donnée par notre MLE. Dans ce cas, le véritable paramètre inconnu se situera dans l’intervalle de crédibilité à 95 % entre 0,23 et 0,57.

Donc, dans le premier cas, vous diriez à votre ami que vous êtes sûr que la pièce est injuste. Mais dans un autre cas, vous lui diriez que vous n’êtes pas sûr que la pièce soit juste.

Comme vous pouvez le voir, même avec les mêmes preuves (2 faces sur 10 lancers), les résultats peuvent être différents en fonction des croyances antérieures. C’est l’un des points forts des statistiques bayésiennes qui, à l’instar de la méthode scientifique, nous permettent de mettre à jour nos croyances en combinant des croyances antérieures avec de nouvelles observations et preuves.

END

Dans l’article d’aujourd’hui, nous avons vu les origines des statistiques bayésiennes et ses principaux contributeurs. Depuis lors, de nombreux autres contributeurs importants ont contribué à ce domaine des statistiques (Jeffreys, Cox, Shannon, etc.), reproduits à partir de quantdare.com.