GARCH-QR नॉनलाइनियर रिग्रेशन (GQNR) ट्रेडिंग मॉडल
 2
2
 1687
1687
कॉपीराइट घोषणाः यदि आप इस लेख को कॉपी करना चाहते हैं, तो कृपया स्रोत का उल्लेख करें। यदि आप इसे व्यावसायिक उद्देश्यों के लिए उपयोग करना चाहते हैं, तो कृपया व्यक्तिगत रूप से लिखें या लेखक से संपर्क करेंः [email protected]
1 परिचय
क्वांटिटेबल लेनदेन के फायदे
क्वांटिटेटिव ट्रेडिंग का तात्पर्य उन्नत गणितीय मॉडल के बजाय मानव-निर्मित व्यक्तिपरक निर्णय है, जो कंप्यूटर तकनीक का उपयोग करने के लिए रणनीतियों को तैयार करने के लिए किया जाता है, जो निवेशकों की भावनाओं के उतार-चढ़ाव के प्रभाव को बहुत कम करता है, जो कि बाजार के अत्यधिक उन्माद या निराशावादी होने पर तर्कहीन निवेश निर्णय लेने से बचता है। डिजिटल मुद्राओं के कारण 24*7 घंटे की निरंतर लेनदेन बाजार की निरंतरता, और मात्रात्मक लेनदेन उच्च आवृत्ति लेनदेन के प्रभाव तक पहुंच सकता है, डिजिटल मुद्रा बाजार शुरू करने के लिए स्पष्ट रूप से एक अच्छी शुरुआत है। वर्तमान में डिजिटल मुद्रा बाजार अभी भी अपरिपक्व है। प्लेटफॉर्म ट्रेडिंग सिस्टम की खराबी, k-लाइन प्लग अभी भी कभी-कभी दिखाई देते हैं, और यह मात्रात्मक लेनदेन के लिए एक जोखिम भी है। हालांकि, डिजिटल मुद्रा के लिए मात्रात्मक लेनदेन करने के लिए कुल मिलाकर, यह अभी भी लाभ से अधिक नुकसान है। क्योंकि मॉडल के प्रशिक्षण और समय श्रृंखला के परीक्षण के माध्यम से, हम सबसे कम समय में सैकड़ों मॉडल में सबसे उपयुक्त तरीके का प्रयास कर सकते हैं।
GQNR मॉडल का विवरण
यह मॉडल गार्च मॉडल पर आधारित है जो अस्थिरता की भविष्यवाणी करता है, जो अस्थिरता की भविष्यवाणी करने वाले VaR मानों के लिए दशमलव वापसी के माध्यम से गैर-रैखिक वापसी का उपयोग करता है, उदाहरण के लिए, GA को भविष्य की अगली अवधि में अधिकतम VaR और न्यूनतम VaR का अनुमान लगाने के लिए संरेखित करता है। इस विधि को GQNR के रूप में संदर्भित किया गया है।
1. गार्च मॉड्यूल
इस खंड में, हम इस रणनीति के गार्च के मूल के बारे में विस्तार से बात करेंगे, जो वित्तीय बाजारों में कुछ व्यापकता है और डिजिटल मुद्राओं पर कुछ पूर्वानुमान प्रभाव तक पहुंचता है।
1.1 गार्च परिभाषा
ARCH मॉडल का सार अवशिष्ट वर्ग अनुक्रम का उपयोग कर q चरणों में एक चलती समतल वर्तमान में अंतर के मान के अनुरूप है। चूंकि एक चलती औसत मॉडल में स्व-संबंधित गुणांक q चरणों का समापन होता है, इसलिए ARCH मॉडल वास्तव में केवल अल्पकालिक स्व-संबंधित गुणांक के लिए उपयुक्त है। लेकिन व्यवहार में, कुछ अवशिष्ट अनुक्रमों के लिए विषम अंतर फ़ंक्शन लंबे समय तक स्व-संबंधित होते हैं, जो ARCH मॉडल के अनुरूप है। इस प्रकार, ARCH मॉडल के अनुरूप अंतर फ़ंक्शन का उपयोग करने से उच्च चलती औसत उत्पन्न होता है, जिससे पैरामीटर का अनुमान लगाना मुश्किल हो जाता है और अंततः ARCH मॉडल की सटीकता को प्रभावित करता है। इस समस्या को ठीक करने के लिए, एक व्यापक स्व-रिवर्जन सशर्त अंतर मॉडल, जिसे GARCH ((p,q) के रूप में संक्षिप्त किया गया है, का सुझाव दिया गया है। GARCH मॉडल वास्तव में ARCH के आधार पर है, जो कि विभेदक फ़ंक्शन को ध्यान में रखते हुए p-वर्ग की स्वतः प्रत्यावर्तनशीलता से बनता है, जो कि लंबे समय तक याद रखने वाले विभेदक फ़ंक्शन को प्रभावी रूप से फिट कर सकता है। ARCH मॉडल GARCH मॉडल का एक विशेष उदाहरण है, p = 0 का GARCH ((p, q) मॉडल) ।
1.2 ARCH प्रक्रिया
यदि σn को n-1 ट्रेडिंग चक्र में एक परिसंपत्ति की गतिशीलता का अनुमान लगाया जाता है, और mu एक दैनिक रिटर्न है, तो एक निष्पक्ष अनुमान हाल ही में m ट्रेडिंग चक्रों के लिए रिटर्न के आधार पर किया जा सकता हैः $\( \sigma *n^2= \frac{1}{m-1} \sum\limits*{i=1}^m {( { \mu_{n-i}- \overline{\mu} } ) ^2}, \)\( निम्नलिखित परिवर्तनों को करें 1μn-i को प्रतिशत रिटर्न में परिवर्तित करें; 2m-1 को m में परिवर्तित करें; 3 मान लें कि μ = 0 है, और इन परिवर्तनों का परिणाम पर बहुत अधिक प्रभाव नहीं पड़ता है, ऊपर दिए गए सूत्र के अनुसार, अस्थिरता को सरल बनाया जा सकता हैः \)\( \sigma *n^2= \frac{1}{m} \sum\limits*{i=1}^m { \mu_{n-i} ^2}, \)\( यह है कि प्रत्येक चक्र के लिए उतार-चढ़ाव की दर के वर्ग के बराबर वजन 1/m है, क्योंकि यह वर्तमान उतार-चढ़ाव का अनुमान है, निकटतम डेटा को अधिक वजन दिया जाना चाहिए, उपरोक्त को बदल दिया जा सकता हैः \)\( \sigma *n^2= \sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}, \)$ एक दीर्घकालिक विचलन दर VL है, और इसका भार γ है, तो यह उपरोक्त सूत्र के अनुसार प्राप्त किया जा सकता हैः
\[ \begin{cases}\sigma *n^2= \gamma V*{L}+\sum\limits_{i=1}^m { \alpha_i\mu_{n-i} ^2}\ &\ \gamma+\sum\limits_{i=1}^m{\alpha_i\mu_{n-i}^2}=1 & \end{cases} , \]
"" " " " " " " " " " " " " " " $\( \sigma *n^2= \omega+\sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}, \)\( इस प्रकार से हम एक सामान्य ARCH () 1) प्रक्रिया प्राप्त कर सकते हैं \)\( \sigma *n^2= \omega+{ \alpha\mu*{n-1} ^2}, \)$
1.3 गार्च प्रक्रिया
GARCH (p,q) मॉडल ARCH (p) और EWMA (q) मॉडल का एक संयोजन है, जिसका अर्थ है कि अस्थिरता न केवल पूर्व p अवधि की आय से संबंधित है, बल्कि स्वयं पूर्व q अवधि से भी संबंधित है, इस प्रकार हैः $\( \sigma *n^2= \omega+\sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}+\sum\limits_{i=1}^m { \beta_i\sigma_{n-i} ^2}, \)\(         उपरोक्त सूत्र के अनुसार हम एक सामान्य GARCH ((1,1)) प्राप्त कर सकते हैंः \)\( \begin{cases}\sigma *n^2= \omega+{ \alpha\mu*{n-1} ^2+\beta\sigma_{n-1}^2}\&\ \qquad\alpha+\beta+\gamma=1 & \end{cases} , \)$
2 क्यूआर मॉड्यूल
इस खंड में, हम मूलभूत अंकों की वापसी और रणनीतिक अंकों के महत्व का वर्णन करेंगे।
2.1 क्यूआर परिभाषा
अंकीय प्रत्यावर्तन एक पद्धति है जो प्रत्यावर्तन चर X के एक सेट और व्याख्या किए जाने वाले चर Y के अंकों के बीच एक रैखिक संबंध का अनुमान लगाने के लिए मॉडलिंग है। पिछले रिटर्न मॉडल वास्तव में व्याख्या किए गए चर की शर्त अपेक्षाओं का अध्ययन करते हैं। और लोगों को यह भी चिंता है कि व्याख्या किए गए चर और व्याख्या किए गए चर के वितरण के माध्य के बीच क्या संबंध है। यह सबसे पहले कोएनकर और बासेट द्वारा 1978 में प्रस्तावित किया गया था। ओएलएस रिटर्न अनुमान की गणना न्यूनतम अवशिष्ट वर्ग पर आधारित है।
2.2 ओएलएस से क्यूआर तक
एक सामान्य वापसी विधि न्यूनतम द्विघात है, जो कि न्यूनतम त्रुटि के वर्ग का योग हैः $\( min \sum{({y_i- \widehat{y}*i })}^2 \)\( जबकि दशमलव का लक्ष्य उपरोक्त सूत्रों के आधार पर न्यूनतम भारित त्रुटि पूर्ण मान और हैः \)\( \mathop{\arg\min*\beta}\ \ \sum{[{\tau(y_i-X_i\beta)^++(1-\tau)(X_i\beta-y_i) ^+ }]} \)$
2.2 क्यूआर दृश्य
आप देख सकते हैं कि सभी नमूनों को अलग-अलग रिक्त स्थान में विभाजित किया गया है, और यह भी एक विभाजन रेखा है
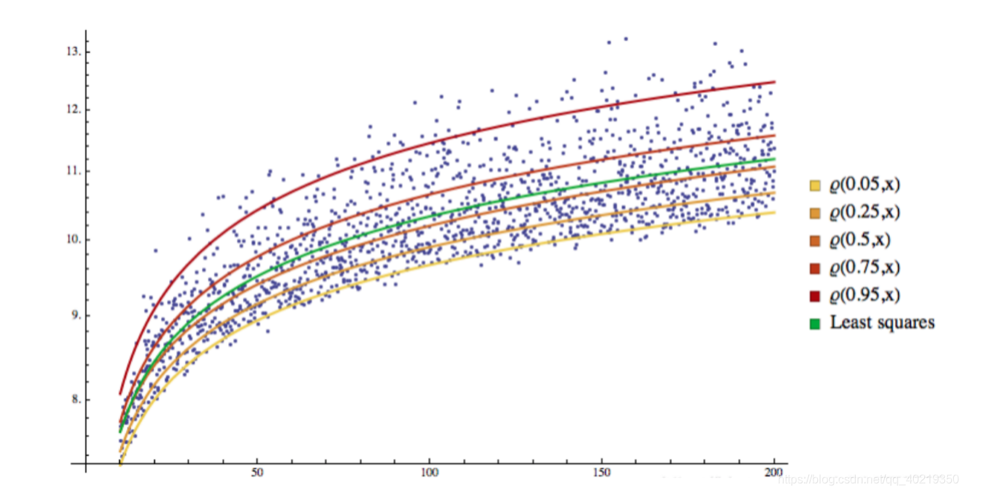
3. GARCH-QR वापसी
हम स्वाभाविक रूप से सोच रहे हैं कि क्या हम बाजार में अज्ञात उतार-चढ़ाव सिग्मा का उपयोग कर सकते हैं और भविष्य में उतार-चढ़ाव के अवमूल्यन की भविष्यवाणी करने के लिए दशमलव Q के साथ वापसी कर सकते हैं।
3.1 वैल्यूएशन दर और वैर के लिए रिटर्न फॉर्म का चयन
इस प्रकार, यह एक प्रकार है, और यह एक प्रकार है, और यह एक प्रकार है, और यह एक प्रकार है, और यह एक प्रकार है, और यह एक प्रकार है, और यह एक प्रकार है। $\( VaR=\epsilon+W^TE\E=(\zeta,\zeta^2,\zeta^3,\zeta^4)\W=(W_1,W_2,W_3,W_4) \)$
3.2 लक्ष्य फ़ंक्शन को परिभाषित करना
ऊपर दी गई जानकारी के आधार पर, हम संयोजन के बाद अंतिम रूप से अनुकूलित करने के लिए लक्ष्य फ़ंक्शन प्राप्त कर सकते हैंः $\( \widehat{W}=\mathop{\arg\min_W}\ \ \sum{[{\alpha(VaR_t-W^TE_t)^++(1-\alpha)(W^TE_t-VaR_t) ^+ }]} \)$
3.3 लक्ष्य फ़ंक्शन का अनुकूलन करने के लिए मशीन लर्निंग का उपयोग करना
इस चरण में अधिक विकल्प हैं, पारंपरिक ग्रेडिएंट कम हो गया है, और आनुवांशिक एल्गोरिदम भी हैं, पाठक अपनी रचनात्मकता का प्रयोग कर सकते हैं। हमने एक अनुकूलित जीए एल्गोरिदम का उपयोग किया है, जिसे हमारे ब्लॉग में विस्तार से बताया गया है, लेकिन अब इसका उपयोग नहीं किया जा रहा है।GA एल्गोरिथ्म के बारे में पता
3. GQNR का उपयोग कैसे करें
1. विचार की निश्चितता
जीक्यूएनआर का मूल यह है कि बाजार में उतार-चढ़ाव के साथ, प्रत्येक वर्तमान समय बिंदु पर, अगले अवधि के उतार-चढ़ाव के लिए भविष्यवाणी करने के लिए गार्च के माध्यम से पूर्वानुमान लगाया जा सकता है, और दूसरी ओर, पिछले डेटा के माध्यम से उतार-चढ़ाव के उतार-चढ़ाव के दशमलव रिटर्न को प्राप्त करने के लिए जो उच्च संभावना के तहत नहीं होगा उतार-चढ़ाव की सीमा ऊपरी सीमा और निचली सीमा। और ये दो सीमाएं, समग्र का मूल हैं। एक बार जब हम ऊपरी सीमा को ट्रिगर करते हैं, तो हम मान सकते हैं कि उच्च संभावना के तहत अल्पावधि में रिवर्स की प्रवृत्ति होगी, और एक बार जब हम निचली सीमा को ट्रिगर करते हैं, तो हम मान सकते हैं कि उच्च संभावना के तहत अल्पावधि में तेजी की प्रवृत्ति होगी।
2. उपयोग में कठिनाई
- वापसी के रूप में
- अनुकूली एल्गोरिदम के विकल्प
- मशीन सीखने के लिए उपयुक्त पैरामीटर
- बाजार की अनिश्चितता और आकस्मिकता
3. समाधान
- रणनीति सीखने के समय चक्र को कम करें
- एकल जमा गारंटी को दीर्घकालिक जोखिम के खिलाफ कम करना
- द्विआधारी सह-सत्यापन और द्विआधारी अवमूल्यन की पुष्टि