पिछले सप्ताह, हमने पेश कियावीएआर जोखिम प्रबंधनजब किसी पोर्टफोलियो के जोखिम की बात की जाती है, तो यह प्रत्येक व्यक्तिगत परिसंपत्ति के जोखिम के बराबर नहीं होता, बल्कि उनके मूल्य सहसंबंध से संबंधित होता है। उदाहरण के तौर पर दो परिसंपत्तियों को लें, अगर उनका सकारात्मक सहसंबंध बहुत मजबूत है, यानी वे एक साथ बढ़ते और गिरते हैं, तो लंबी अवधि के निवेशों में विविधता लाने से जोखिम कम नहीं होगा। अगर नकारात्मक सहसंबंध बहुत मजबूत है, तो विविधीकरण जोखिम को काफी हद तक कम कर सकता है। स्वाभाविक प्रश्न यह है कि पोर्टफोलियो में निवेश करते समय आप एक निश्चित स्तर के जोखिम पर अधिकतम लाभ कैसे प्राप्त करते हैं? यहीं पर मार्कोविट्ज़ सिद्धांत लागू होता है, जिसका मैं आज परिचय दूंगा।

आधुनिक पोर्टफोलियो सिद्धांत (एमपीटी), 1952 में हैरी मार्कोविट्ज द्वारा प्रस्तावित, पोर्टफोलियो चयन के लिए एक गणितीय ढांचा है जिसका उद्देश्य विभिन्न जोखिमपूर्ण परिसंपत्ति संयोजनों का चयन करके अपेक्षित रिटर्न को अधिकतम करना है। एमपीटी जोखिमों को नियंत्रित करते हुए लाभ कमाता है। मूल विचार यह है कि परिसंपत्तियों की कीमतें पूर्ण समन्वय में नहीं चलती हैं (अर्थात् परिसंपत्तियों के बीच अपूर्ण सहसंबंध होता है) तथा परिसंपत्ति आवंटन में विविधता लाकर समग्र निवेश जोखिम को कम किया जा सकता है।

मार्कोविट्ज़ सिद्धांत की प्रमुख अवधारणाएँ

1. अपेक्षित प्रतिफल दरयह वह रिटर्न है जिसकी कोई निवेशक किसी परिसंपत्ति या पोर्टफोलियो को धारण करके उम्मीद कर सकता है, जिसका अनुमान आमतौर पर ऐतिहासिक रिटर्न डेटा के आधार पर लगाया जाता है।

   \(E(R_p) = \sum_{i=1}^{n} w_i E(R_i)\)

   जहाँ \(E(R_p)\) पोर्टफोलियो की वापसी की अपेक्षित दर है, \(wi\) पोर्टफोलियो में \(i\)वीं परिसंपत्ति का भार है, और \(E(R_i)\) पोर्टफोलियो की वापसी की अपेक्षित दर है। i$th संपत्ति..

2. **जोखिम (अस्थिरता या मानक विचलन)**निवेश रिटर्न की अनिश्चितता या निवेश की अस्थिरता को मापने के लिए उपयोग किया जाता है।

   \(\sigma_p = \sqrt{\sum_{i=1}^{n} \sum_{j=1}^{n} w_i w_j \sigma_{ij}}\)

   जहां \(\sigma_p\) पोर्टफोलियो का कुल जोखिम है और \(\sigma_{ij}\) परिसंपत्ति \(i\) और परिसंपत्ति \(j\) के बीच सहप्रसरण है, जो दो परिसंपत्तियों के मूल्य परिवर्तनों के बीच संबंध को मापता है।

3. सहप्रसरण: दो परिसंपत्तियों के मूल्य आंदोलनों के बीच सहसंबंध को मापता है।

   \(\sigma_{ij} = \rho_{ij} \sigma_i \sigma_j\)

   जहाँ \(\rho_{ij}\) परिसंपत्ति \(i\) और परिसंपत्ति \(j\) के बीच सहसंबंध गुणांक है, \(\sigma_i\) और \(\sigma_j\) क्रमशः परिसंपत्ति \(i\) और परिसंपत्ति \(j\) के मानक विचलन हैं।

4. कुशल सीमांतजोखिम-रिटर्न समन्वय प्रणाली में, कुशल फ्रंटियर उन पोर्टफोलियो का समूह है जो किसी दिए गए जोखिम स्तर पर अधिकतम अपेक्षित रिटर्न प्रदान कर सकता है।

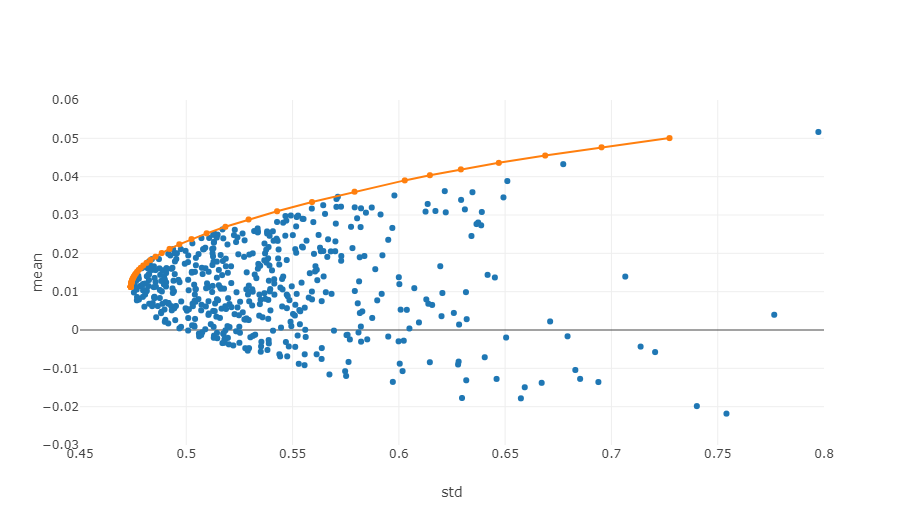
ऊपर दिया गया चित्र प्रभावी सीमा का एक योजनाबद्ध आरेख है। प्रत्येक बिंदु अलग-अलग भार वाले निवेश पोर्टफोलियो को दर्शाता है। क्षैतिज अक्ष अस्थिरता है, अर्थात जोखिम स्तर, और ऊर्ध्वाधर अक्ष वापसी की दर है। स्पष्टतः, हम ग्राफ के ऊपरी किनारे पर ध्यान केंद्रित करते हैं, जो समान जोखिम स्तर पर उच्चतम रिटर्न प्राप्त करता है।

मात्रात्मक व्यापार और पोर्टफोलियो प्रबंधन में, इन सिद्धांतों को लागू करने के लिए ऐतिहासिक आंकड़ों के सांख्यिकीय विश्लेषण और विभिन्न परिसंपत्तियों के अपेक्षित रिटर्न, मानक विचलन और सहप्रसरण का अनुमान लगाने के लिए गणितीय मॉडल के उपयोग की आवश्यकता होती है। फिर, सर्वोत्तम परिसंपत्ति भार विन्यास खोजने के लिए अनुकूलन तकनीकों को लागू किया जाता है। इस प्रक्रिया में आमतौर पर जटिल गणितीय गणनाएं और बहुत सारी कंप्यूटर प्रोसेसिंग शामिल होती है, यही कारण है कि आधुनिक वित्त में मात्रात्मक विश्लेषण बहुत महत्वपूर्ण हो गया है। निम्नलिखित में अनुकूलन करने के तरीके को समझाने के लिए एक विशिष्ट पायथन उदाहरण का उपयोग किया जाएगा।

सिमुलेशन विधि का उपयोग करके इष्टतम संयोजन खोजने के लिए पायथन कोड उदाहरण

मार्कोविट्ज़ इष्टतम पोर्टफोलियो की गणना एक बहु-चरणीय प्रक्रिया है जिसमें डेटा तैयारी, पोर्टफोलियो सिमुलेशन और संकेतक गणना जैसे कई प्रमुख चरण शामिल हैं। संदर्भ: https://plotly.com/python/v3/ipython-notebooks/markowitz-portfolio-optimization/

1. बाज़ार डेटा प्राप्त करें：

   • उत्तीर्णget_dataचयनित डिजिटल मुद्रा का ऐतिहासिक मूल्य डेटा प्राप्त करने का फ़ंक्शन। यह रिटर्न और जोखिम की दर की गणना करने के लिए आवश्यक डेटा है, जिसका उपयोग पोर्टफोलियो बनाने और शार्प अनुपात की गणना करने के लिए किया जाता है।

2. रिटर्न और जोखिम की गणना：

   • उपयोगcalculate_returns_riskयह फ़ंक्शन प्रत्येक डिजिटल मुद्रा के लिए वार्षिक रिटर्न दर और वार्षिक जोखिम (मानक विचलन) की गणना करता है। इसका उद्देश्य इष्टतम पोर्टफोलियो में उपयोग के लिए प्रत्येक परिसंपत्ति के ऐतिहासिक प्रदर्शन का आकलन करना है।

3. मार्कोविट्ज़ इष्टतम पोर्टफोलियो की गणना करें：

   • उपयोगcalculate_optimal_portfolioफ़ंक्शन, एकाधिक पोर्टफोलियो का अनुकरण। प्रत्येक सिमुलेशन में, परिसंपत्ति भार यादृच्छिक रूप से उत्पन्न किए जाते हैं और फिर इन भारों के आधार पर पोर्टफोलियो के अपेक्षित रिटर्न और जोखिम की गणना की जाती है।
   • विभिन्न भारों के संयोजनों को यादृच्छिक रूप से उत्पन्न करके, सर्वोत्तम संयोजन खोजने के लिए कई संभावित पोर्टफोलियो का पता लगाया जा सकता है। यह मार्कोविट्ज़ के पोर्टफोलियो सिद्धांत के मूल विचारों में से एक है।

पूरी प्रक्रिया का लक्ष्य ऐसा पोर्टफोलियो ढूंढना है जो किसी निश्चित जोखिम स्तर पर सर्वोत्तम अपेक्षित रिटर्न दे। कई संभावित संयोजनों का अनुकरण करके, निवेशक बेहतर ढंग से समझ सकते हैं कि विभिन्न विन्यास कैसे प्रदर्शन करेंगे और वह संयोजन चुन सकते हैं जो उनके निवेश उद्देश्यों और जोखिम सहनशीलता के लिए सबसे उपयुक्त हो। यह दृष्टिकोण निवेश निर्णयों को अनुकूलित करने और निवेश को अधिक कुशल बनाने में मदद करता है।

            
            
            
import numpy as np
import pandas as pd
import requests
import matplotlib.pyplot as plt

# 获取行情数据
def get_data(symbols):
    data = []
    for symbol in symbols:
        url = 'https://api.binance.com/api/v3/klines?symbol=%s&interval=%s&limit=1000'%(symbol,'1d')
        res = requests.get(url)
        data.append([float(line[4]) for line in res.json()])
    return data

def calculate_returns_risk(data):
    returns = []
    risks = []

    for d in data:
        daily_returns = np.diff(d) / d[:-1]
        annualized_return = np.mean(daily_returns) * 365
        annualized_volatility = np.std(daily_returns) * np.sqrt(365)

        returns.append(annualized_return)
        risks.append(annualized_volatility)

    return np.array(returns), np.array(risks)

# 计算马科维茨最优组合
def calculate_optimal_portfolio(returns, risks):
    n_assets = len(returns)
    num_portfolios = 3000

    results = np.zeros((4, num_portfolios), dtype=object) 


    for i in range(num_portfolios):
        weights = np.random.random(n_assets)
        weights /= np.sum(weights)

        portfolio_return = np.sum(returns * weights)
        portfolio_risk = np.sqrt(np.dot(weights.T, np.dot(np.cov(returns, rowvar=False), weights)))

        results[0, i] = portfolio_return
        results[1, i] = portfolio_risk
        results[2, i] = portfolio_return / portfolio_risk
        results[3, i] = list(weights) # 将权重转换为列表

    return results

symbols = ['BTCUSDT','ETHUSDT', 'BNBUSDT','LINKUSDT','BCHUSDT','LTCUSDT']
data = get_data(symbols)

returns, risks = calculate_returns_risk(data)
optimal_portfolios = calculate_optimal_portfolio(returns, risks)

max_sharpe_idx = np.argmax(optimal_portfolios[2])
optimal_return = optimal_portfolios[0, max_sharpe_idx]
optimal_risk = optimal_portfolios[1, max_sharpe_idx]
optimal_weights = optimal_portfolios[3, max_sharpe_idx]

# 输出结果
print("最优组合:")
for i in range(len(symbols)):
    print(f"{symbols[i]}权重: {optimal_weights[i]:.4f}")

print(f"预期收益率: {optimal_return:.4f}")
print(f"预期风险(标准差): {optimal_risk:.4f}")
print(f"夏普比率: {optimal_return / optimal_risk:.4f}")

# 可视化投资组合
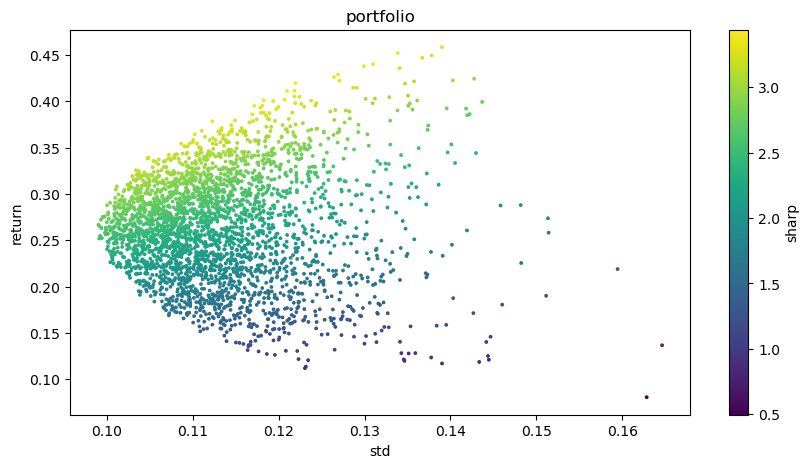
plt.figure(figsize=(10, 5))
plt.scatter(optimal_portfolios[1], optimal_portfolios[0], c=optimal_portfolios[2], marker='o', s=3)
plt.title('portfolio')
plt.xlabel('std')
plt.ylabel('return')
plt.colorbar(label='sharp')
plt.show()

अंतिम आउटपुट:
सर्वोत्तम संयोजन:
BTCUSDT वजन: 0.0721
ETHUSDT वजन: 0.2704
BNBUSDT वजन: 0.3646
LINKUSDT वजन: 0.1892
BCHUSDT वजन: 0.0829
LTCUSDT वजन: 0.0209
अपेक्षित रिटर्न दर: 0.4195
अपेक्षित जोखिम (मानक विचलन): 0.1219
शार्प अनुपात: 3.4403