बायेसियन: संभाव्यता के रहस्य को समझना और निर्णय लेने के पीछे गणितीय ज्ञान की खोज करना
 0
0
 1340
1340

बायेसियन सांख्यिकी गणित का एक शक्तिशाली विषय है जिसका वित्त, चिकित्सा अनुसंधान और सूचना प्रौद्योगिकी सहित कई क्षेत्रों में व्यापक अनुप्रयोग है। यह हमें पूर्व विश्वासों को साक्ष्यों के साथ संयोजित करके नए पश्च विश्वासों तक पहुंचने की अनुमति देता है, जिससे हम अधिक सूचित निर्णय ले पाते हैं।
इस लेख में हम इस क्षेत्र की स्थापना करने वाले कुछ प्रमुख गणितज्ञों का संक्षिप्त परिचय देंगे।
बेयस से पहले बेयेसियन सांख्यिकी को बेहतर ढंग से समझने के लिए, हमें 18वीं शताब्दी में वापस जाना होगा और गणितज्ञ डी मोइवर और उनके पेपर “द प्रिंसिपल ऑफ चांस” का संदर्भ लेना होगा।[1]。
अपने ग्रंथ में, डी मोइवर ने संभाव्यता और जुए से संबंधित अपने समय की कई समस्याओं पर चर्चा की। जैसा कि आप शायद जानते हैं, इनमें से एक समस्या के उनके समाधान से सामान्य वितरण की उत्पत्ति हुई, लेकिन यह एक अलग कहानी है।
उनके पेपर में एक सरल प्रश्न है:
“एक निष्पक्ष सिक्के को लगातार तीन बार उछालने पर तीन बार सिर आने की संभावना।”
“संभावना का सिद्धांत” में वर्णित समस्याओं को पढ़ते हुए, आप देख सकते हैं कि उनमें से अधिकांश एक परिकल्पना से शुरू होती हैं, जिसके आधार पर किसी दी गई घटना की संभावना की गणना की जाती है। उदाहरण के लिए, उपरोक्त समस्या में, यह धारणा है कि सिक्का निष्पक्ष है, इसलिए उछालने पर चित आने की संभावना 0.5 है।
इसे आज गणितीय शब्दों में इस प्रकार व्यक्त किया जाता है:
𝑃(𝑋|𝜃)
लेकिन क्या होगा अगर हमें यह पता न हो कि सिक्का सही है या नहीं? यदि हम नहीं जानते𝜃ऊनी कपड़े?
थॉमस बेयस और रिचर्ड प्राइस
लगभग पचास साल बाद, 1763 में, “संभावना के सिद्धांत पर एक निबंध” शीर्षक से एक पेपर प्रकाशित हुआ।[2] रॉयल सोसाइटी ऑफ लंदन के फिलॉसॉफिकल ट्रांजेक्शन में प्रकाशित।
दस्तावेज़ के पहले कुछ पन्नों में गणितज्ञ रिचर्ड प्राइस द्वारा लिखित एक पाठ है, जिसमें उनके मित्र थॉमस बेयस द्वारा उनकी मृत्यु से कुछ वर्ष पहले लिखे गए एक पेपर की विषय-वस्तु का सारांश दिया गया है। भूमिका में प्राइस ने थॉमस बेयस द्वारा की गई कुछ खोजों के महत्व को समझाया है, जिनका उल्लेख डी मोइवर के ‘प्रिंसिपल्स ऑफ चांस’ में नहीं किया गया था।
वास्तव में, वह एक विशिष्ट समस्या की ओर इशारा कर रहे थे:
“किसी अज्ञात घटना के घटित होने और असफल होने की संख्या दी हुई है, तो उसके घटित होने की संभावना, प्रायिकता की किसी भी दो नामित डिग्री के बीच में होने की संभावना ज्ञात कीजिए।”
दूसरे शब्दों में, किसी घटना का अवलोकन करने के बाद, हम अज्ञात पैरामीटर का पता लगाते हैंθदो संभाव्यता डिग्री के बीच संभाव्यता क्या है? यह वास्तव में सांख्यिकीय अनुमान से संबंधित इतिहास की पहली समस्याओं में से एक है, और इसी से व्युत्क्रम संभाव्यता नाम की उत्पत्ति हुई। गणितीय शब्दों में:
𝑃( 𝜃 | 𝑋)
यह वही है जिसे आज हम बेयस प्रमेय का पश्च वितरण कहते हैं।
अकारण कारण
इन दो वरिष्ठ पादरियों के बारे में जानिए।थॉमस बेयसऔररिचर्ड प्राइसवास्तव में, शोध को प्रेरित करने वाली बात बहुत दिलचस्प है। लेकिन ऐसा करने के लिए हमें कुछ समय के लिए सांख्यिकी के बारे में अपने ज्ञान को अलग रखना होगा।
हम 18वीं सदी में हैं और गणितज्ञों के लिए प्रायिकता एक बढ़ती हुई रुचि का क्षेत्र बनता जा रहा है। डी मोइवर या बर्नौली जैसे गणितज्ञों ने दर्शाया था कि कुछ घटनाएं एक निश्चित सीमा तक यादृच्छिकता के साथ घटित होती हैं, लेकिन फिर भी वे निश्चित नियमों द्वारा नियंत्रित होती हैं। उदाहरण के लिए, यदि आप एक पासे को कई बार फेंकते हैं, तो छः में से एक बार वह छः पर आएगा। ऐसा लगता है जैसे कोई छिपा हुआ नियम है जो भाग्य का निर्धारण करता है।
अब कल्पना कीजिए कि आप एक गणितज्ञ और एक आस्थावान आस्तिक हैं और इस काल में रह रहे हैं। आपको यह जानने में दिलचस्पी होगी कि यह छिपा हुआ नियम परमेश्वर से कैसे जुड़ा है।
यह वही प्रश्न है जो बेयस और प्राइस ने स्वयं पूछा था। इस समस्या को हल करने के लिए वे जिस समाधान की आशा कर रहे थे, वह सीधे तौर पर यह साबित करने पर लागू होता था कि “दुनिया बुद्धि और विवेक का परिणाम होनी चाहिए; इस प्रकार अंतिम कारण के रूप में ईश्वर के अस्तित्व का सबूत मिलता है”[2] - अर्थात, कोई कारण और प्रभाव नहीं है।
लाप्लास
आश्चर्य की बात है कि लगभग दो साल बाद, 1774 में, जाहिर तौर पर थॉमस बेयस के पेपर को पढ़े बिना, फ्रांसीसी गणितज्ञ लाप्लास ने “इवेंट्स की संभावनाओं के माध्यम से घटनाओं के कारणों पर” शीर्षक से एक पेपर लिखा।[3], जो व्युत्क्रम संभाव्यता समस्या पर एक पेपर है। पहले पेज पर आप पढ़ सकते हैं
मुख्य सिद्धांत इस प्रकार हैं:
“यदि किसी घटना के n अलग-अलग कारण हो सकते हैं, तो किसी दी गई घटना के लिए इन कारणों की संभावनाएं कारण दिए गए घटना की संभावना के बराबर अनुपात में होती हैं, और इनमें से प्रत्येक कारण के अस्तित्व की संभावना बराबर होती है घटना की संभावना को कारण दिए जाने पर। कारणों की संभावना, उन प्रत्येक कारणों को देखते हुए घटना की संभावनाओं के योग से विभाजित।
इसे आज हम बेयेस प्रमेय के नाम से जानते हैं:
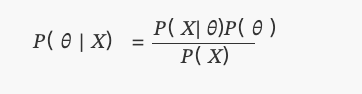
मेंP(θ)समान रूप से वितरित है.
सिक्का प्रयोग
हम पायथन और PyMC लाइब्रेरी का उपयोग करके और एक सरल प्रयोग करके बायेसियन सांख्यिकी को वर्तमान में लाएंगे।
मान लीजिए कि आपका कोई मित्र आपको एक सिक्का देता है और पूछता है कि क्या आपको लगता है कि यह सिक्का उचित है। क्योंकि वह जल्दी में है, वह आपको सिक्का केवल 10 बार उछालने के लिए कहता है। जैसा कि आप देख सकते हैं, इस समस्या में एक अज्ञात पैरामीटर हैp, एक सिक्का उछालने पर सिर आने की संभावना, और हम इसका अनुमान लगाना चाहते हैंpका सबसे संभावित मान है।
(नोट: हम मापदंडों के बारे में बात नहीं कर रहे हैंpएक यादृच्छिक चर है, लेकिन यह पैरामीटर निश्चित है और हम जानना चाहते हैं कि किन मूल्यों के बीच इसकी सबसे अधिक संभावना है। )
इस समस्या पर एक अलग दृष्टिकोण प्राप्त करने के लिए, हम इसे दो अलग-अलग पूर्व मान्यताओं के तहत संबोधित करेंगे:
-
- आपको सिक्के की निष्पक्षता के बारे में कोई पूर्व जानकारी नहीं है और आप समान संभावनाएं देते हैं
p. इस मामले में, हम असूचनात्मक पूर्वधारणा का प्रयोग करेंगे, क्योंकि आप अपने विश्वास में कोई जानकारी नहीं जोड़ रहे हैं।
- आपको सिक्के की निष्पक्षता के बारे में कोई पूर्व जानकारी नहीं है और आप समान संभावनाएं देते हैं
-
- आप अनुभव से जानते हैं कि भले ही कोई सिक्का अनुचित हो, लेकिन उसे बहुत अनुचित बनाना कठिन है, इसलिए आपको लगता है कि पैरामीटर
pअधिकतर सम्भावना यह है कि यह 0.3 से नीचे या 0.7 से ऊपर नहीं जायेगा। इस मामले में, हम एक सूचनात्मक पूर्वसूचना का उपयोग करेंगे।
- आप अनुभव से जानते हैं कि भले ही कोई सिक्का अनुचित हो, लेकिन उसे बहुत अनुचित बनाना कठिन है, इसलिए आपको लगता है कि पैरामीटर
दोनों मामलों में, हमारी पूर्व मान्यताएं इस प्रकार होंगी:
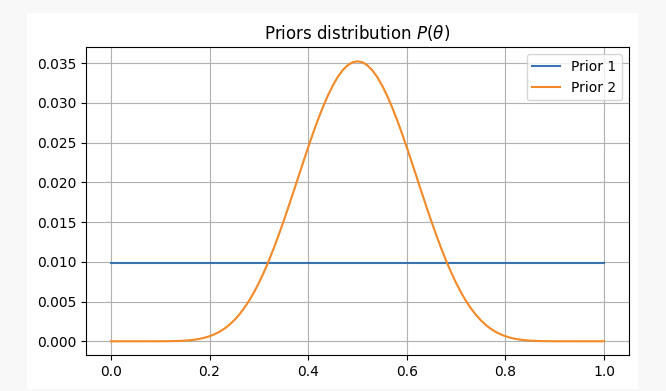
एक सिक्के को 10 बार उछालने पर दो बार चित आता है। इस साक्ष्य के साथ, हम संभवतः यह पता लगा सकेंगे कि हमें अपने पैरामीटर कहां मिलेंगेp?
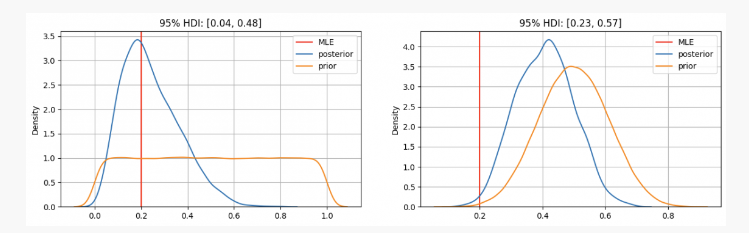
जैसा कि आप देख सकते हैं, पहले मामले में हमारे पास हैpका पूर्व वितरण अधिकतम संभावना अनुमान (एमएलई) पर केंद्रित हैp=0.2, जो फ्रीक्वेंटिस्ट पद्धति का उपयोग करने वाला एक समान दृष्टिकोण है। वास्तविक अज्ञात पैरामीटर 0.04 और 0.48 के बीच 95% विश्वसनीय अंतराल के भीतर होगा।
दूसरी ओर, जब इस बात का उच्च विश्वास हो कि पैरामीटरp जबकि यह 0.3 और 0.7 के बीच होना चाहिए, हम देख सकते हैं कि पश्च वितरण 0.4 के आसपास है, जो हमारे MLE द्वारा दिए गए मान से बहुत अधिक है। इस मामले में, वास्तविक अज्ञात पैरामीटर 0.23 और 0.57 के बीच 95% विश्वसनीय अंतराल के भीतर होगा।
तो पहले मामले में, आप अपने मित्र को बताएंगे कि आपको पूरा विश्वास है कि सिक्का अनुचित है। लेकिन दूसरे मामले में, आप उससे कहेंगे कि आप इस बात को लेकर निश्चित नहीं हैं कि सिक्का सही है या नहीं।
जैसा कि आप देख सकते हैं, समान साक्ष्य (10 में से 2 बार सिर) के साथ भी, विभिन्न पूर्व मान्यताओं के आधार पर परिणाम भिन्न हो सकते हैं। यह बायेसियन सांख्यिकी की ताकत है, जो वैज्ञानिक पद्धति के समान, हमें पूर्व विश्वासों को नए अवलोकनों और साक्ष्यों के साथ जोड़कर अपने विश्वासों को अद्यतन करने की अनुमति देती है।
END
आज के लेख में हमने बायेसियन सांख्यिकी की उत्पत्ति और इसके मुख्य योगदानकर्ताओं के बारे में देखा। तब से, सांख्यिकी के इस क्षेत्र में कई अन्य महत्वपूर्ण योगदानकर्ता हुए हैं (जेफरीज़, कॉक्स, शैनन, आदि), जिन्हें quantdare.com से पुन: प्रस्तुत किया गया है।