तंत्रिका नेटवर्क अंतर मूल्य उतार-चढ़ाव अनुकूलन मात्रात्मक व्यापार रणनीति
ATR ANN TANH OHLC4 volatility TIMEFRAME NEURAL NETWORK MACHINE LEARNING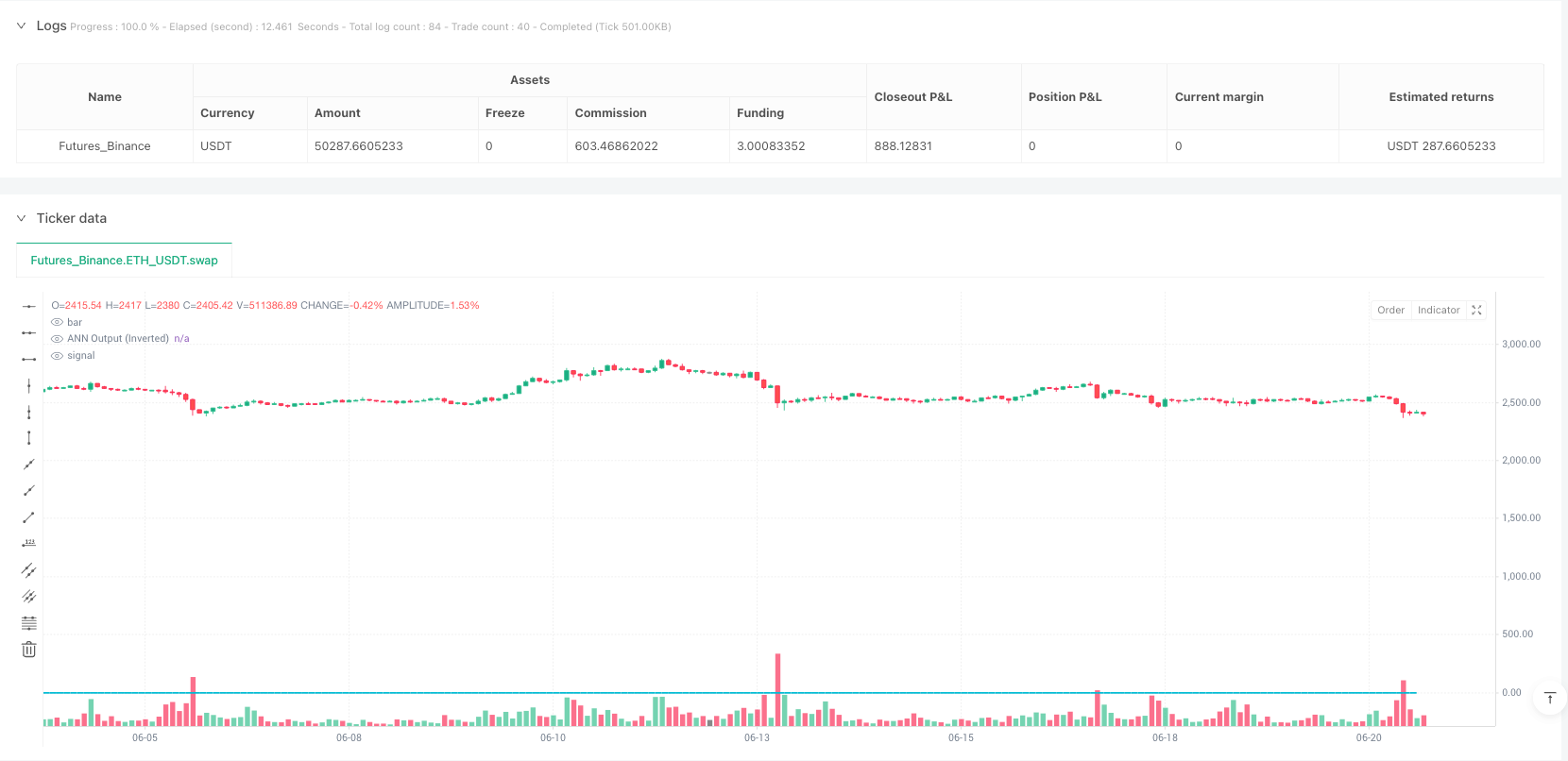
अवलोकन
न्यूरल नेटवर्क अंतर मूल्य उतार-चढ़ाव अनुकूलन क्वांटिफाइड ट्रेडिंग रणनीति एक कृत्रिम तंत्रिका नेटवर्क (एएनएन) पर आधारित एक उच्च आवृत्ति ट्रेडिंग प्रणाली है, जो 1 सेकंड के स्तर के लिए समय सीमा अनुकूलन के लिए डिज़ाइन की गई है। यह रणनीति न्यूरल नेटवर्क का उपयोग करती है जो अल्पकालिक मूल्य परिवर्तन अंतर का विश्लेषण करती है, आगे की ओर प्रसारण एल्गोरिदम के माध्यम से मूल्य की दिशा की भविष्यवाणी करती है, और व्यापार निर्णयों को अनुकूलित करने के लिए अस्थिरता दर फ़िल्टर और सत्र समय नियंत्रण के साथ संयुक्त होती है। रणनीति का मुख्य भाग सूक्ष्म मूल्य परिवर्तन पैटर्न को पकड़ने में है, उच्च आवृत्ति वातावरण में उच्च लाभप्रदता कारक 3.754 के स्थिर व्यापार प्रदर्शन को प्राप्त करने के लिए।
रणनीति सिद्धांत
यह रणनीति एक तीन-स्तरीय तंत्रिका नेटवर्क वास्तुकला का उपयोग करती है, जो आगे के प्रसारण एल्गोरिदम के माध्यम से मूल्य अंतर डेटा को संसाधित करती हैः
इनपुट लेयर: वर्तमान ओएचएलसी 4 (उच्च और निम्न औसत मूल्य) और संदर्भ समय फ़्रेम (डिफ़ॉल्ट 15 सेकंड) में ऐतिहासिक ओएचएलसी 4 के प्रतिशत अंतर को एक एकल इनपुट न्यूरॉन के रूप में प्राप्त करना।
पहली छिपी हुई परत: इसमें 5 न्यूरॉन्स होते हैं, जो इनपुट डेटा को गैर-रैखिक रूप से परिवर्तित करने के लिए सक्रियण फ़ंक्शन के रूप में द्विवक्रता का उपयोग करते हैं। प्रत्येक न्यूरॉन में मूल्य अंतर को पकड़ने के लिए एक विशिष्ट पैटर्न के लिए पूर्व-प्रशिक्षित भार होते हैं।
दूसरी छिपी हुई परत: इसमें 33 न्यूरॉन्स होते हैं, जो पहले छिपे हुए परत के आउटपुट को और अधिक जटिल भार मैट्रिक्स के माध्यम से संसाधित करने के लिए tanh सक्रियण फ़ंक्शन का उपयोग करते हैं।
आउटपुट परत: एक एकल न्यूरॉन एक अंतिम पूर्वानुमानित सिग्नल का उत्पादन करता है, जिसका मूल्य सिग्नल की दिशा को संशोधित करने के लिए उलट दिया जाता है।
लेन-देन तर्क तंत्रिका नेटवर्क के आउटपुट मान ((L3_0) के आसपास विकसित होता हैः
- जब L3_0 इनपुट थ्रेशोल्ड से बड़ा होता है (डिफ़ॉल्ट 0.003), तो मल्टी सिग्नल ट्रिगर करें
- जब L3_0 शून्य से कम है तो रिक्त सिग्नल को ट्रिगर करें
- जब L3_0 बाहर निकलने के थ्रेशोल्ड से कम होता है (डिफ़ॉल्ट 0.001) तो मल्टीहेड को क्लियर करें
- जब L3_0 ऋणात्मक बाहर निकलने के थ्रेशोल्ड से अधिक है (−0.001), तो स्थिति को खाली करें
इस रणनीति में तीन प्रकार के फ़िल्टरिंग तंत्र भी शामिल हैंः
- शीतलन फ़िल्टर: लेन-देन के बाद, सिस्टम को निर्दिष्ट शीतलन अवधि (डिफ़ॉल्ट 60 सेकंड) का इंतजार करना होगा
- फ़िल्टर करेंएटीआर (Average True Range) सूचक के माध्यम से, केवल तभी ट्रेड करें जब बाजार में उतार-चढ़ाव न्यूनतम सीमा (डिफ़ॉल्ट 0.02) से अधिक हो
- लेनदेन समय फ़िल्टरवैकल्पिक रूप से व्यापार को केवल विशिष्ट बाजार के समय पर प्रतिबंधित करें (डिफ़ॉल्ट 9:00 से 16:00)
रणनीतिक लाभ
उच्च सटीक भविष्यवाणी क्षमता: तंत्रिका नेटवर्क की बहु-स्तरीय संरचना मूल्य आंदोलन में जटिल गैर-रैखिक संबंधों को पकड़ने में सक्षम है, जो पारंपरिक तकनीकी संकेतकों के लिए मुश्किल है। विशेष रूप से उच्च आवृत्ति वातावरण में, यह संरचना अल्पकालिक मूल्य पैटर्न की पहचान कर सकती है और अधिक सटीक प्रवेश और निकास संकेत प्रदान कर सकती है।
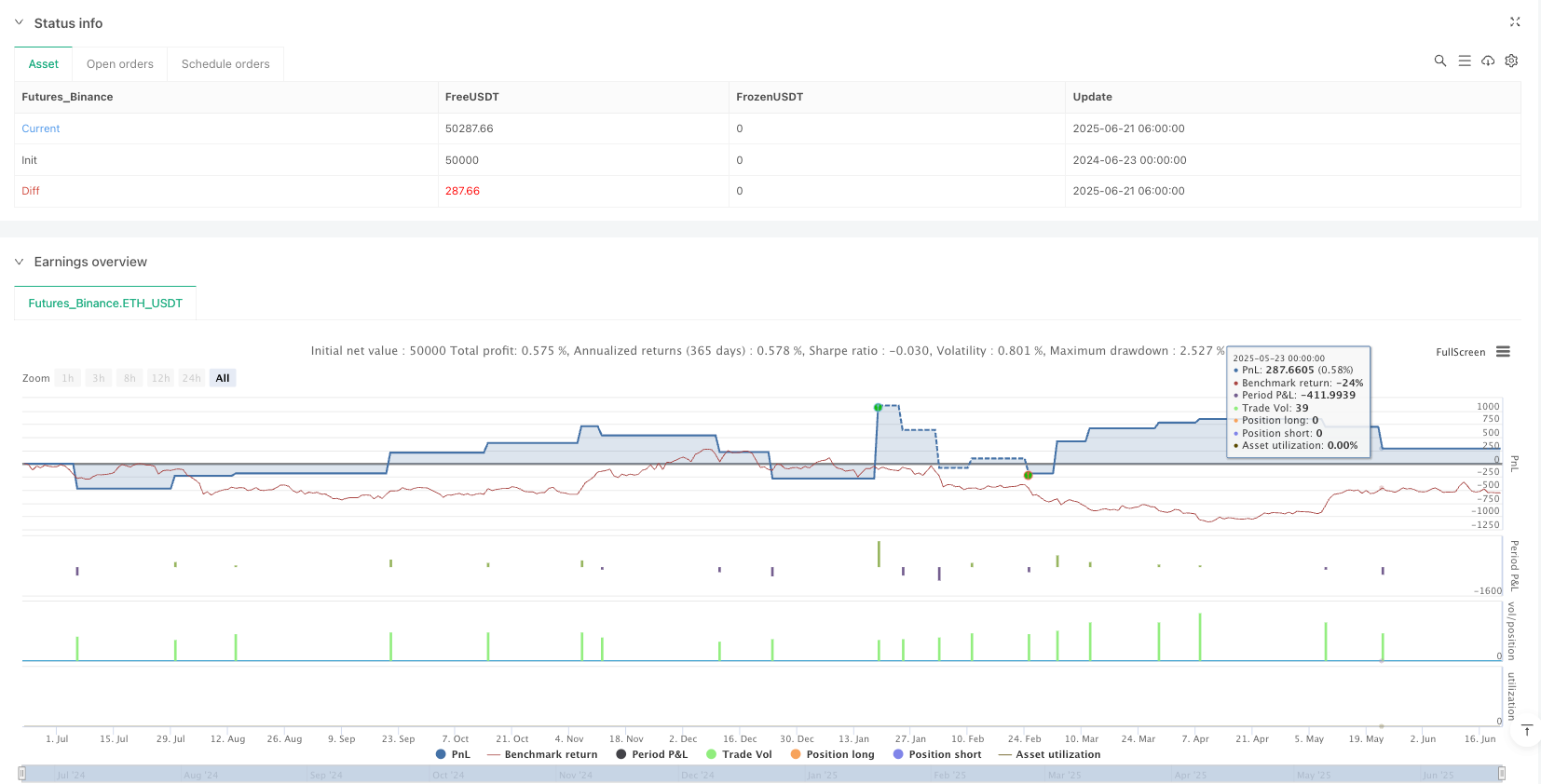
उत्कृष्ट जोखिम-लाभ अनुपात: रणनीति 3.754 के लाभ कारक को प्राप्त करती है, जिसका अर्थ है कि कुल लाभदायक लेनदेन कुल घाटे वाले लेनदेन का 3.754 गुना है, जो एक मात्रात्मक रणनीति में बहुत अच्छा प्रदर्शन है।
लचीला पैरामीटर अनुकूलन अंतरिक्ष: रणनीति में कई समायोज्य पैरामीटर शामिल हैं, जिसमें प्रवेश / निकास थ्रेशोल्ड, शीतलन अवधि की लंबाई, संदर्भ समय सीमा और न्यूनतम अस्थिरता आवश्यकताएं शामिल हैं, जिससे व्यापारी विभिन्न बाजार स्थितियों और व्यापार प्रकारों के लिए अनुकूलन कर सकते हैं।
मल्टीफ़िल्टरिंगट्रेडों की गुणवत्ता को बढ़ाने के लिए, रणनीति को ठंडा करने की अवधि, अस्थिरता और ट्रेडिंग समय के तीन फिल्टर को एकीकृत करके अनावश्यक ट्रेडिंग और झूठे संकेतों को कम करने के लिए प्रभावी है।
उच्च आवृत्ति व्यापार वातावरण के लिए अनुकूलन: 1 सेकंड के स्तर पर समय सीमा के लिए अनुकूलित, जो अल्पकालिक मूल्य में उतार-चढ़ाव से लाभ के अवसरों को पकड़ने के लिए उच्च आवृत्ति वाले ट्रेडिंग की विशेषताओं का लाभ उठाता है।
कम देरी: रणनीति कोड संरचना स्पष्ट और कुशल है, न्यूरल नेटवर्क भाग पूर्व-प्रशिक्षण भार का उपयोग करके सीधे गणना करता है, वास्तविक समय प्रशिक्षण की आवश्यकता नहीं है, उच्च आवृत्ति वातावरण में कम विलंबता निष्पादन सुनिश्चित करता है।
रणनीतिक जोखिम
अति-अनुरूपता का जोखिम: तंत्रिका नेटवर्क मॉडल में बहुत सारे पूर्वनिर्धारित भारित पैरामीटर शामिल हैं, जो ऐतिहासिक डेटा के अति-फिट होने का जोखिम है। इससे रणनीति को वास्तविक व्यापार में कम प्रदर्शन करने का कारण बन सकता है, खासकर जब बाजार की स्थिति में महत्वपूर्ण परिवर्तन होते हैं। प्रतिक्रिया में तंत्रिका नेटवर्क को नियमित रूप से फिर से प्रशिक्षित करना, लंबे समय तक चलने वाले डेटा का उपयोग करके सत्यापन करना और मजबूत जोखिम प्रबंधन उपायों को लागू करना शामिल है।
पैरामीटर संवेदनशीलता: रणनीति का प्रदर्शन अत्यधिक कई पैरामीटर सेटिंग्स पर निर्भर करता है, जैसे कि प्रवेश / निकास थ्रेशोल्ड, शीतलन अवधि की लंबाई, आदि। पैरामीटर में मामूली परिवर्तन से रणनीति के प्रदर्शन में भारी उतार-चढ़ाव हो सकता है। स्थिर पैरामीटर संयोजन खोजने और अति-अनुकूलन से बचने के लिए पैरामीटर स्कैन और चरण परीक्षण के माध्यम से सलाह दी जाती है।
उच्च आवृत्ति ट्रेडिंग जोखिम1: 1 सेकंड के समय के फ्रेम पर, लेनदेन की लागत (जैसे अंतर और स्लाइड) रणनीतियों की लाभप्रदता को काफी प्रभावित कर सकती है। इन लागतों को वास्तविक लेनदेन से पहले और वास्तविक लेनदेन की लागत स्थितियों को अनुकरण करने के लिए पर्याप्त रूप से विचार किया जाना चाहिए।
तकनीकी चुनौतियाँउच्च आवृत्ति रणनीतियों के लिए, ट्रेडिंग सिस्टम को बहुत कम विलंबता और उच्च विश्वसनीयता की आवश्यकता होती है। किसी भी नेटवर्क विलंबता, डेटा विलंबता या निष्पादन विलंबता से रणनीति विफल हो सकती है। पेशेवर स्तर के ट्रेडिंग बुनियादी ढांचे और कम विलंबता डेटा स्रोतों का उपयोग सुनिश्चित करें।
बाजार में उतार-चढ़ाव का जोखिम: चरम बाजार स्थितियों में (जैसे कि अचानक समाचार या तरलता की कमी), तंत्रिका नेटवर्क मॉडल कीमतों के आंदोलनों की सटीक भविष्यवाणी करने में असमर्थ हो सकते हैं, जिससे भारी नुकसान होता है। स्टॉप लॉस उपायों और अधिकतम दैनिक हानि सीमाओं को स्थापित करने और चरम उतार-चढ़ाव के दौरान रणनीति को निलंबित करने की सिफारिश की जाती है।
रणनीति अनुकूलन दिशा
तंत्रिका नेटवर्क वास्तुकला अनुकूलन:
- मॉडल की भविष्यवाणी क्षमता को बढ़ाने के लिए अधिक इनपुट सुविधाओं, जैसे कि लेनदेन की मात्रा, अस्थिरता सूचक और मूल्य गतिशीलता सूचक को शामिल करने पर विचार करें
- विभिन्न छिपी परत संरचनाओं और न्यूरॉन्स की संख्या के साथ प्रयास करना, जटिलता और सामान्यीकरण क्षमता के बीच सबसे अच्छा संतुलन खोजने के लिए
- अन्य सक्रियण फ़ंक्शंस (जैसे ReLU या Leaky ReLU) के प्रभाव का पता लगाएं, जो कुछ तंत्रिका नेटवर्क अनुप्रयोगों में tanh से बेहतर प्रदर्शन करते हैं
गतिशील पैरामीटर समायोजन तंत्र:
- बाजार की स्थिति के आधार पर अनुकूलन योग्य प्रवेश/निकास थ्रेशोल्ड को प्राप्त करना, जैसे कि उच्च अस्थिरता वाले वातावरण में थ्रेशोल्ड को बढ़ाना और कम अस्थिरता वाले वातावरण में थ्रेशोल्ड को कम करना
- उतार-चढ़ाव की धारणा के लिए शीतकालीन समायोजन एल्गोरिदम विकसित करना, ताकि रणनीति विभिन्न बाजार चरणों में इष्टतम ट्रेडिंग आवृत्ति बनाए रख सके
एकीकृत पूर्वानुमान ढांचा:
- एक समग्र पूर्वानुमान संकेत के लिए कई समय फ्रेम के साथ संयोजन में तंत्रिका नेटवर्क मॉडल
- मशीन लर्निंग मेटा-मॉडल को पेश करना, विभिन्न भविष्यवाणी मॉडल के लिए गतिशील रूप से वजन समायोजित करना
- इस पद्धति से एकल मॉडल की सीमाओं को कम किया जा सकता है और भविष्यवाणी की स्थिरता में सुधार किया जा सकता है।
जोखिम प्रबंधन में सुधार:
- मॉडल विश्वसनीयता और बाजार की स्थिति के आधार पर व्यापार के पैमाने को समायोजित करने के लिए गतिशील स्थिति प्रबंधन प्रणाली विकसित करना
- प्रति लेनदेन जोखिम-लाभ अनुपात को अनुकूलित करने के लिए मशीन-लर्निंग-आधारित स्टॉप-लॉस रणनीतियों को पेश करना
- दिन के समय का अनुकूलन करें, दिन में सबसे अच्छा प्रदर्शन करने वाली रणनीतियों की पहचान करें
वास्तविक समय में सीखना और अनुकूलन:
- ऑनलाइन सीखने के लिए डिज़ाइन किया गया तंत्र, जिससे तंत्रिका नेटवर्क लगातार नए डेटा से सीख सकते हैं और बाजार में बदलाव के लिए अनुकूल हो सकते हैं
- प्रदर्शन निगरानी के आधार पर स्वचालित पुनः प्रशिक्षण ट्रिगर को लागू करना, रणनीति के प्रदर्शन में गिरावट पर मॉडल को सक्रिय रूप से अपडेट करना
- इस तरह के दृष्टिकोण से रणनीतियों का जीवनकाल और स्थिरता में काफी सुधार हो सकता है।
संक्षेप
न्यूरल नेटवर्क अंतर मूल्य में उतार-चढ़ाव के अनुकूलन के लिए क्वांटिफाइंग ट्रेडिंग रणनीति आधुनिक क्वांटिफाइंग ट्रेडिंग के अग्रणी अभ्यास का प्रतिनिधित्व करती है, जो उच्च आवृत्ति वाले ट्रेडिंग के क्षेत्र में कृत्रिम तंत्रिका नेटवर्क तकनीक को सफलतापूर्वक लागू करती है। सावधानीपूर्वक डिजाइन की गई बहु-स्तरीय तंत्रिका नेटवर्क संरचना के माध्यम से, रणनीति अल्पकालिक मूल्य परिवर्तनों में सूक्ष्म पैटर्न को पकड़ने में सक्षम है, और कई फ़िल्टरिंग तंत्रों के माध्यम से ट्रेडिंग की गुणवत्ता में सुधार करती है।
3.754 का लाभप्रदता कारक परीक्षण वातावरण में रणनीति के उत्कृष्ट प्रदर्शन को दर्शाता है, लेकिन वास्तविक अनुप्रयोगों में अभी भी अत्यधिक अनुकूलन, पैरामीटर संवेदनशीलता और उच्च आवृत्ति ट्रेडिंग के लिए विशिष्ट जोखिमों पर सावधानीपूर्वक विचार करना आवश्यक है। तंत्रिका नेटवर्क वास्तुकला के निरंतर अनुकूलन, गतिशील पैरामीटर समायोजन को लागू करने और जोखिम प्रबंधन को बढ़ाने के माध्यम से, रणनीति में प्रतिस्पर्धी मात्रात्मक ट्रेडिंग क्षेत्र में दीर्घकालिक प्रतिस्पर्धा बनाए रखने की क्षमता है।
रणनीति की एक महत्वपूर्ण सफलता कारक जटिल तंत्रिका नेटवर्क तकनीक को व्यावहारिक व्यापारिक तर्क के साथ जोड़ना है, जो मशीन सीखने की भविष्यवाणी क्षमता का उपयोग करता है और वास्तविक व्यापार की व्यवहार्यता को ध्यान में रखता है। अनुभवी मात्रात्मक व्यापारियों के लिए, यह एक स्केलेबल फ्रेमवर्क प्रदान करता है जिसे विभिन्न बाजारों और व्यक्तिगत जोखिम वरीयताओं के अनुसार आगे अनुकूलित और अनुकूलित किया जा सकता है।
/*backtest
start: 2024-06-23 00:00:00
end: 2025-06-21 08:00:00
period: 2h
basePeriod: 2h
exchanges: [{"eid":"Futures_Binance","currency":"ETH_USDT"}]
*/
//@version=5
strategy("ANN Strategy v2 (Optimized for 1s)", overlay=true, default_qty_type=strategy.percent_of_equity, default_qty_value=100)
// === INPUTS ===
entryThreshold = input.float(0.003, title="Entry Threshold")
exitThreshold = input.float(0.001, title="Exit Threshold")
cooldownBars = input.int(60, title="Cooldown (bars)") // 60 seconds cooldown
timeframe = input.timeframe("1", title="Reference Timeframe") // 1-minute diff reference
minVolatility = input.float(0.02, title="Min ATR (Volatility Filter)")
useSession = input.bool(true, title="Use Session Filter")
// === UTILITY FUNCTIONS ===
getDiff() =>
prev = request.security(syminfo.tickerid, timeframe, ohlc4[1])
now = ohlc4
(now - prev) / prev
linear(v) => v
tanh(v) => (math.exp(v) - math.exp(-v)) / (math.exp(v) + math.exp(-v))
// === ANN FORWARD PROPAGATION ===
l0_0 = linear(getDiff())
l1 = array.new_float()
array.push(l1, tanh(l0_0 * 0.8446488687))
array.push(l1, tanh(l0_0 * -0.5674069006))
array.push(l1, tanh(l0_0 * 0.8676766445))
array.push(l1, tanh(l0_0 * 0.5200611473))
array.push(l1, tanh(l0_0 * -0.2215499554))
// === Layer 2 weights ===
w2 = array.from( 0.3341657935, -2.0060003664, 0.8606354375, 0.9184846912, -0.8531172267, -0.0394076437, -0.4720374911, 0.2900968524, 1.0653326022, 0.3000188806, -0.559307785, -0.9353655177, 1.2133832962, 0.1952686024, 0.8552068166, -0.4293220754, 0.8484259409, -0.7154087313, 0.1102971055, 0.2279392724, 0.9111779155, 0.2801691115, 0.0039982713, -0.5648257117, 0.3281705155, -0.2963954503, 0.4046532178, 0.2460580977, 0.6608675819, -0.8732022547, 0.8810811932, 0.6903706878, -0.5953059103, -0.3084040686, -0.4038498853, -0.5687101164, 0.2736758588, -0.2217360382, 0.8742950972, 0.2997583987, 0.0708459913, 0.8221730616, -0.7213265567, -0.3810462836, 0.0503867753, 0.4880140595, 0.9466627196, 1.0163097961, -0.9500386514, -0.6341709382, 1.3402207103, 0.0013395288, 3.4813009133, -0.8636814677, 41.3171047132, 1.2388217292, -0.6520886912, 0.3508321737, 0.6640560714, 1.5936220597, -0.1800525171, -0.2620989752, 0.056675277, -0.5045395315, 0.2732553554, -0.7776331454, 0.1895231137, 0.5384918862, 0.093711904, -0.3725627758, -0.3181583022, 0.2467979854, 0.4341718676, -0.7277619935, 0.1799381758, -0.5558227731, 0.3666152536, 0.1538243225, -0.8915928174, -0.7659355684, 0.6111516061, -0.5459495224, -0.5724238425, -0.8553500765, -0.8696190472, 0.6843667454, 0.408652181, -0.8830470112, -0.8602324935, 0.1135462621, -0.1569048216, -1.4643247888, 0.5557152813, 1.0482791924, 1.4523116833, 0.5207514017, -0.2734444192, -0.3328660936, -0.7941515963, -0.3536051491, -0.4097807954, 0.3198619826, 0.461681627, -0.1135575498, 0.7103339851, -0.8725014237, -1.0312091401, 0.2267643037, -0.6814258121, 0.7524828703, -0.3986855003, 0.4962556631, -0.7330224516, 0.7355772164, 0.3180141739, -1.083080442, 1.8752543187, 0.3623326265, -0.348145191, 0.1977935038, -0.0291290625, 0.0612906199, 0.1219696687, -1.0273685429, 0.0872219768, 0.931791094, -0.313753684, -0.3028724837, 0.7387076712, 0.3806140391, 0.2630619402, -1.9827996702, -0.7741413496, 0.1262957444, 0.2248777886, -0.2666322362, -1.124654664, 0.7288282621, -0.1384289204, 0.2395966188, 0.6611845175, 0.0466048937, -0.1980999993, 0.8152350927, 0.0032723211, -0.3150344751, 0.1391754608, 0.5462816249, -0.7952302364, -0.7520712378, -0.0576916066, 0.3678415302, 0.6802537378, 1.1437036331, -0.8637405666, 0.7016273068, 0.3978601709, 0.3157049654, -0.2528455662, -0.8614146703, 1.1741126834, -1.4046408959, 1.2914477803, 0.9904052964, -0.6980155826)
l2 = array.new_float()
for i = 0 to 32
sum = 0.0
for j = 0 to 4
weight = array.get(w2, i * 5 + j)
sum += weight * array.get(l1, j)
array.push(l2, tanh(sum))
// === Output layer weights ===
weights_out = array.from( -0.1366382003, 0.8161960822, -0.9458773183, 0.4692969576, 0.0126710629, -0.0403001012, -0.0116244898, -0.4874816289, -0.6392241448, -0.410338398, -0.1181027081, 0.1075562037, -0.5948728252, 0.5593677345, -0.3642935247, -0.2867603217, 0.142250271, -0.0535698019, -0.034007685, -0.3594532426, 0.2551095195, 0.4214344983, 0.8941621336, 0.6283377368, -0.7138020667, -0.1426738249, 0.172671223, 0.0714824385, -0.3268182144, -0.0078989755, -0.2032828145, -0.0260631534, 0.4918037012)
sum_out = 0.0
for i = 0 to array.size(l2) - 1
sum_out += array.get(weights_out, i) * array.get(l2, i)
// === Final ANN output (inverted for signal correction) ===
l3_0 = -tanh(sum_out)
// === TRADE FILTERS ===
volatility = ta.atr(14)
isVolOkay = volatility > minVolatility
isSession = (hour >= 9 and hour < 16) // Adjust to your market hours
sessionOkay = useSession ? isSession : true
// === SIGNAL LOGIC ===
var string activeTrade = "none"
var int lastTradeBar = na
canTrade = (na(lastTradeBar) or (bar_index - lastTradeBar > cooldownBars)) and isVolOkay and sessionOkay
enterLong = l3_0 > entryThreshold and activeTrade != "long" and canTrade
exitLong = l3_0 < exitThreshold and activeTrade == "long"
enterShort = l3_0 < -entryThreshold and activeTrade != "short" and canTrade
exitShort = l3_0 > -exitThreshold and activeTrade == "short"
// === STRATEGY EXECUTION ===
if barstate.isrealtime
if enterLong
strategy.entry("Long", strategy.short)
activeTrade := "long"
lastTradeBar := bar_index
if exitLong
strategy.close("Long")
activeTrade := "none"
if enterShort
strategy.entry("Short", strategy.long)
activeTrade := "short"
lastTradeBar := bar_index
if exitShort
strategy.close("Short")
activeTrade := "none"
// === PLOTTING ===
bgcolor(activeTrade == "long" ? color.new(color.green, 85) : activeTrade == "short" ? color.new(color.red, 85) : na)
plot(l3_0, title="ANN Output (Inverted)", color=color.aqua, linewidth=2)