Minggu lalu, kami memperkenalkanManajemen Risiko VaRKetika berbicara tentang risiko portofolio, risikonya tidak sama dengan risiko setiap aset individu, tetapi terkait dengan korelasi harganya. Mengambil dua aset sebagai contoh, jika korelasi positifnya sangat kuat, yaitu keduanya naik dan turun bersamaan, maka diversifikasi investasi jangka panjang tidak akan mengurangi risiko. Jika korelasi negatifnya sangat kuat, diversifikasi dapat mengurangi risiko secara signifikan. Pertanyaan yang muncul adalah, ketika berinvestasi dalam portofolio, bagaimana Anda memaksimalkan keuntungan pada tingkat risiko tertentu? Di sinilah teori Markowitz, yang akan saya perkenalkan hari ini, berperan.

Teori Portofolio Modern (MPT), yang diusulkan oleh Harry Markowitz pada tahun 1952, adalah kerangka matematika untuk pemilihan portofolio yang bertujuan untuk memaksimalkan pengembalian yang diharapkan dengan memilih berbagai kombinasi aset berisiko. keuntungan sambil mengendalikan risiko. Gagasan intinya adalah bahwa harga aset tidak bergerak dalam sinkronisasi yang sempurna (yaitu, ada korelasi yang tidak sempurna antara aset), dan risiko investasi secara keseluruhan dapat dikurangi dengan mendiversifikasi alokasi aset.

Konsep Kunci Teori Markowitz

1. Tingkat pengembalian yang diharapkan: Ini adalah pengembalian yang diharapkan diperoleh investor dengan memegang aset atau portofolio, biasanya diprediksi berdasarkan data pengembalian historis.

\(E(R_p) = \sum_{i=1}^{n} w_i E(R_i)\)

Dimana \(E(R_p)\) adalah tingkat pengembalian yang diharapkan dari portofolio, \(wi\) adalah bobot aset ke-\(i\) dalam portofolio, dan \(E(R_i)\) adalah tingkat pengembalian yang diharapkan dari $ aset ke-i.

1. Risiko (volatilitas atau deviasi standar): Digunakan untuk mengukur ketidakpastian hasil investasi atau volatilitas investasi.

\(\sigma_p = \sqrt{\sum_{i=1}^{n} \sum_{j=1}^{n} w_i w_j \sigma_{ij}}\)

Di mana \(\sigma_p\) adalah total risiko portofolio dan \(\sigma_{ij}\) adalah kovariansi antara aset \(i\) dan aset \(j\), yang mengukur hubungan antara perubahan harga kedua aset.

1. Kovariansi: Mengukur korelasi antara pergerakan harga dua aset.

\(\sigma_{ij} = \rho_{ij} \sigma_i \sigma_j\)

Di mana \(\rho_{ij}\) adalah koefisien korelasi antara aset \(i\) dan aset \(j\), \(\sigma_i\) dan \(\sigma_j\) masing-masing adalah deviasi standar aset \(i\) dan aset \(j\).

1. Batasan Efisien:Dalam sistem koordinat risiko-imbal hasil, batas efisien adalah serangkaian portofolio yang dapat memberikan imbal hasil maksimum yang diharapkan pada tingkat risiko tertentu.

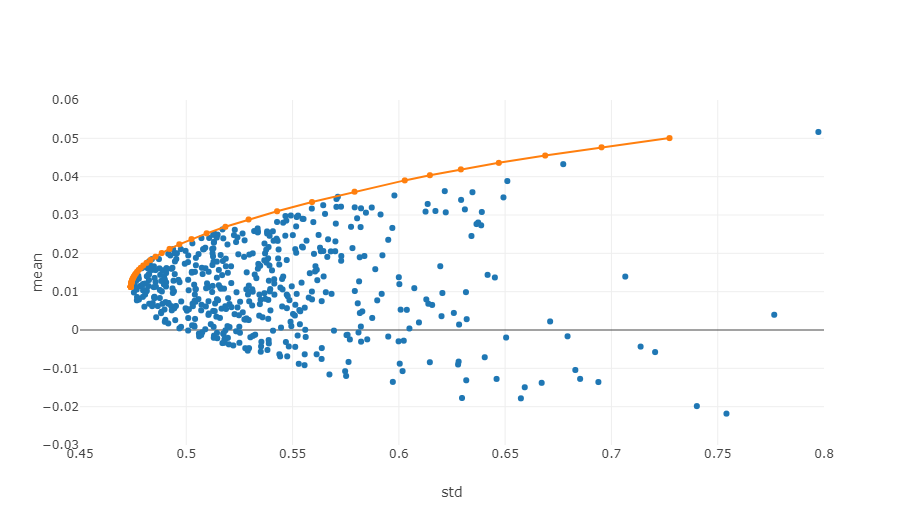
Gambar di atas adalah diagram skema batas efektif. Setiap titik mewakili portofolio investasi dengan bobot yang berbeda. Sumbu horizontal adalah volatilitas, yaitu tingkat risiko, dan sumbu vertikal adalah tingkat pengembalian. Jelasnya, kami fokus pada tepi atas grafik, yang mencapai hasil tertinggi pada tingkat risiko yang sama.

Dalam perdagangan kuantitatif dan manajemen portofolio, penerapan prinsip-prinsip ini memerlukan analisis statistik data historis dan penggunaan model matematika untuk memperkirakan pengembalian yang diharapkan, deviasi standar, dan kovariansi berbagai aset. Kemudian, teknik optimasi diterapkan untuk menemukan konfigurasi bobot aset terbaik. Proses ini biasanya melibatkan perhitungan matematika yang rumit dan banyak pemrosesan komputer, itulah sebabnya analisis kuantitatif menjadi sangat penting dalam keuangan modern. Berikut ini akan menggunakan contoh Python khusus untuk mengilustrasikan cara mengoptimalkan.

Contoh kode Python untuk menemukan kombinasi optimal menggunakan metode simulasi

Menghitung portofolio optimal Markowitz adalah proses multi-langkah yang melibatkan beberapa langkah utama seperti persiapan data, simulasi portofolio, dan kalkulasi indikator. Referensi: https://plotly.com/python/v3/ipython-notebooks/markowitz-portfolio-optimization/

1. Dapatkan data pasar：

   • lulusget_dataBerfungsi untuk mendapatkan data harga historis mata uang digital yang dipilih. Ini adalah data yang diperlukan untuk menghitung tingkat pengembalian dan risiko, yang digunakan untuk membangun portofolio dan menghitung rasio Sharpe.

2. Perhitungan Pengembalian dan Risiko：

   • menggunakancalculate_returns_riskFungsi ini menghitung tingkat pengembalian tahunan dan risiko tahunan (deviasi standar) untuk setiap mata uang digital. Hal ini dilakukan untuk mengukur kinerja historis setiap aset agar dapat digunakan dalam portofolio optimal.

3. Hitung portofolio optimal Markowitz：

   • menggunakancalculate_optimal_portfolioFungsi, simulasi beberapa portofolio. Dalam setiap simulasi, bobot aset dibuat secara acak dan ekspektasi pengembalian serta risiko portofolio kemudian dihitung berdasarkan bobot ini.
   • Dengan menghasilkan kombinasi bobot yang berbeda secara acak, beberapa kemungkinan portofolio dapat dieksplorasi untuk menemukan kombinasi terbaik. Ini adalah salah satu ide inti teori portofolio Markowitz.

Sasaran dari keseluruhan proses ini adalah untuk menemukan portofolio yang memberikan hasil pengembalian yang diharapkan terbaik untuk tingkat risiko tertentu. Dengan mensimulasikan beberapa kemungkinan kombinasi, investor dapat lebih memahami kinerja konfigurasi yang berbeda dan memilih kombinasi yang paling sesuai dengan tujuan investasi dan toleransi risiko mereka. Pendekatan ini membantu mengoptimalkan keputusan investasi dan membuat investasi lebih efisien.

import numpy as np
import pandas as pd
import requests
import matplotlib.pyplot as plt

# 获取行情数据
def get_data(symbols):
    data = []
    for symbol in symbols:
        url = 'https://api.binance.com/api/v3/klines?symbol=%s&interval=%s&limit=1000'%(symbol,'1d')
        res = requests.get(url)
        data.append([float(line[4]) for line in res.json()])
    return data

def calculate_returns_risk(data):
    returns = []
    risks = []

    for d in data:
        daily_returns = np.diff(d) / d[:-1]
        annualized_return = np.mean(daily_returns) * 365
        annualized_volatility = np.std(daily_returns) * np.sqrt(365)

        returns.append(annualized_return)
        risks.append(annualized_volatility)

    return np.array(returns), np.array(risks)

# 计算马科维茨最优组合
def calculate_optimal_portfolio(returns, risks):
    n_assets = len(returns)
    num_portfolios = 3000

    results = np.zeros((4, num_portfolios), dtype=object) 


    for i in range(num_portfolios):
        weights = np.random.random(n_assets)
        weights /= np.sum(weights)

        portfolio_return = np.sum(returns * weights)
        portfolio_risk = np.sqrt(np.dot(weights.T, np.dot(np.cov(returns, rowvar=False), weights)))

        results[0, i] = portfolio_return
        results[1, i] = portfolio_risk
        results[2, i] = portfolio_return / portfolio_risk
        results[3, i] = list(weights) # 将权重转换为列表

    return results

symbols = ['BTCUSDT','ETHUSDT', 'BNBUSDT','LINKUSDT','BCHUSDT','LTCUSDT']
data = get_data(symbols)

returns, risks = calculate_returns_risk(data)
optimal_portfolios = calculate_optimal_portfolio(returns, risks)

max_sharpe_idx = np.argmax(optimal_portfolios[2])
optimal_return = optimal_portfolios[0, max_sharpe_idx]
optimal_risk = optimal_portfolios[1, max_sharpe_idx]
optimal_weights = optimal_portfolios[3, max_sharpe_idx]

# 输出结果
print("最优组合:")
for i in range(len(symbols)):
    print(f"{symbols[i]}权重: {optimal_weights[i]:.4f}")

print(f"预期收益率: {optimal_return:.4f}")
print(f"预期风险(标准差): {optimal_risk:.4f}")
print(f"夏普比率: {optimal_return / optimal_risk:.4f}")

# 可视化投资组合
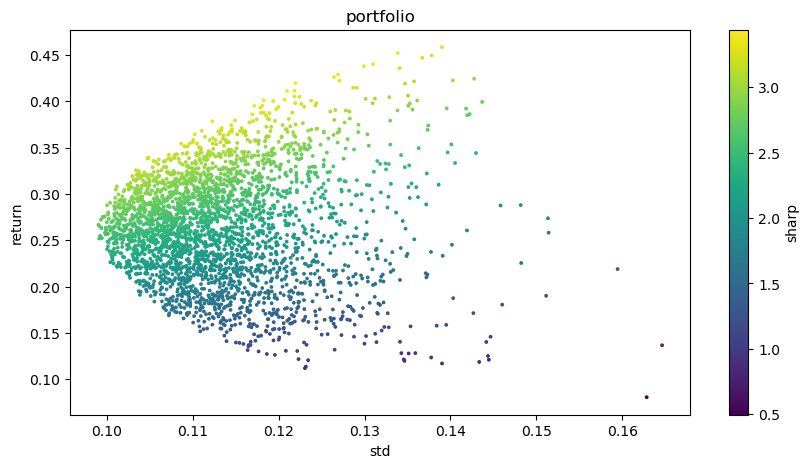
plt.figure(figsize=(10, 5))
plt.scatter(optimal_portfolios[1], optimal_portfolios[0], c=optimal_portfolios[2], marker='o', s=3)
plt.title('portfolio')
plt.xlabel('std')
plt.ylabel('return')
plt.colorbar(label='sharp')
plt.show()

Hasil akhir: Kombinasi terbaik: Berat BTCUSDT: 0,0721 Berat ETHUSDT: 0,2704 Berat BNBUSDT: 0,3646 Berat LINKUSDT: 0,1892 Berat BCHUSDT: 0,0829 Berat LTCUSDT: 0,0209 Hasil yang diharapkan: 0,4195 Risiko yang diharapkan (deviasi standar): 0,1219 Rasio Sharpe: 3.4403