先週ご紹介したVaRリスク管理ポートフォリオのリスクについて話す場合、それは個々の資産のリスクと同じではなく、それらの価格相関に関連しています。 2 つの資産を例にとると、それらの正の相関が非常に強い場合、つまり、一緒に上昇したり下降したりする場合、長期投資を分散してもリスクは軽減されません。負の相関が非常に強い場合は、分散することでリスクを大幅に軽減できます。当然の疑問は、ポートフォリオに投資する場合、特定のリスクレベルでどのように収益を最大化するかということです。ここで、今日紹介するマーコウィッツ理論が役に立ちます。

1952 年にハリー・マーコウィッツによって提唱された現代ポートフォリオ理論 (MPT) は、さまざまなリスク資産の組み合わせを選択することで期待収益を最大化し、リスクを管理しながら利益を上げることを目的としたポートフォリオ選択の数学的フレームワークです。基本的な考え方は、資産価格は完全に同期して動くわけではない（つまり、資産間には不完全な相関関係がある）ため、資産配分を分散することで全体的な投資リスクを軽減できるというものです。

マーコウィッツ理論の主要概念

1. 期待収益率これは、投資家が資産またはポートフォリオを保有することで得られると期待できる収益であり、通常は過去の収益データに基づいて予測されます。

   \(E(R_p) = \sum_{i=1}^{n} w_i E(R_i)\)

   ここで、\(E(R_p)\)はポートフォリオの期待収益率、\(wi\)はポートフォリオの\(i\)番目の資産のウェイト、\(E(R_i)\)は\(の期待収益率である。 i\)番目の資産。

2. リスク（ボラティリティまたは標準偏差）: 投資収益の不確実性または投資の変動性を測定するために使用されます。

   \(\sigma_p = \sqrt{\sum_{i=1}^{n} \sum_{j=1}^{n} w_i w_j \sigma_{ij}}\)

   ここで、\(\sigma_p\) はポートフォリオの総リスクであり、\(\sigma_{ij}\) は資産 \(i\) と資産 \(j\) 間の共分散であり、2 つの資産の価格変動の関係を測定します。

3. 共分散: 2 つの資産の価格変動の相関関係を測定します。

   \(\sigma_{ij} = \rho_{ij} \sigma_i \sigma_j\)

   ここで、\(\rho_{ij}\)は資産\(i\)と資産\(j\)間の相関係数、\(\sigma_i\)と\(\sigma_j\)はそれぞれ資産\(i\)と資産\(j\)の標準偏差です。

4. 効率的フロンティアリスク・リターン座標系において、効率的フロンティアとは、与えられたリスクレベルで最大の期待リターンを提供できるポートフォリオの集合です。

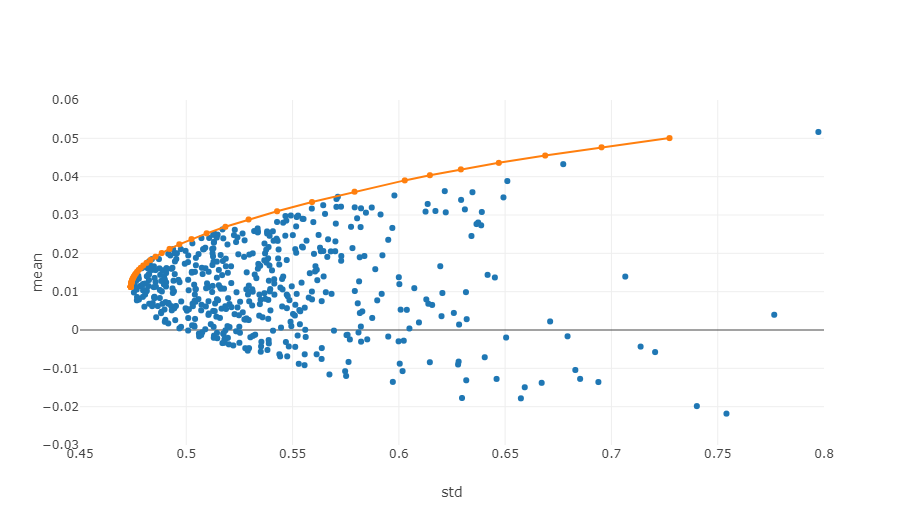
上図は有効フロンティアの模式図です。各点は異なるウェイトを持つ投資ポートフォリオを表しています。横軸はボラティリティ、つまりリスクレベル、縦軸は収益率です。当然のことながら、私たちは同じリスクレベルで最高のリターンを達成するグラフの上端に焦点を当てます。

定量的取引とポートフォリオ管理において、これらの原則を適用するには、履歴データの統計分析と、さまざまな資産の期待収益、標準偏差、共分散を推定するための数学モデルの使用が必要です。次に、最適化技術を適用して、最適な資産の重み構成を見つけます。このプロセスには通常、複雑な数学的計算と大量のコンピューター処理が伴うため、現代の金融では定量分析が非常に重要になっています。以下では、特定の Python の例を使用して最適化の方法を説明します。

シミュレーション法を使用して最適な組み合わせを見つけるための Python コード例

マルコウィッツ最適ポートフォリオの計算は、データの準備、ポートフォリオのシミュレーション、指標の計算など、いくつかの重要なステップを含む複数のステップからなるプロセスです。参考: https://plotly.com/python/v3/ipython-notebooks/markowitz-portfolio-optimization/

1. 市場データを取得する：

   • 合格get_data選択したデジタル通貨の過去の価格データを取得する機能。これは、ポートフォリオの構築やシャープレシオの計算に使用される収益率とリスクを計算するために必要なデータです。

2. リターンとリスクの計算：

   • 使用calculate_returns_riskこの関数は、各デジタル通貨の年間収益率と年間リスク (標準偏差) を計算します。これは、最適なポートフォリオで使用するために各資産の過去のパフォーマンスを定量化するためです。

3. マーコウィッツ最適ポートフォリオを計算する：

   • 使用calculate_optimal_portfolio複数のポートフォリオをシミュレートする機能。各シミュレーションでは、資産の重みがランダムに生成され、その重みに基づいてポートフォリオの期待収益とリスクが計算されます。
   • 異なる重みの組み合わせをランダムに生成することで、複数の可能なポートフォリオを調査し、最適な組み合わせを見つけることができます。これは、マーコウィッツのポートフォリオ理論の中心的な考え方の 1 つです。

プロセス全体の目標は、与えられたリスクレベルに対して最高の期待収益をもたらすポートフォリオを見つけることです。複数の可能な組み合わせをシミュレートすることで、投資家はさまざまな構成のパフォーマンスをよりよく理解し、投資目的とリスク許容度に最も適した組み合わせを選択できます。このアプローチは、投資決定を最適化し、投資をより効率的にするのに役立ちます。

            
            
            
import numpy as np
import pandas as pd
import requests
import matplotlib.pyplot as plt

# 获取行情数据
def get_data(symbols):
    data = []
    for symbol in symbols:
        url = 'https://api.binance.com/api/v3/klines?symbol=%s&interval=%s&limit=1000'%(symbol,'1d')
        res = requests.get(url)
        data.append([float(line[4]) for line in res.json()])
    return data

def calculate_returns_risk(data):
    returns = []
    risks = []

    for d in data:
        daily_returns = np.diff(d) / d[:-1]
        annualized_return = np.mean(daily_returns) * 365
        annualized_volatility = np.std(daily_returns) * np.sqrt(365)

        returns.append(annualized_return)
        risks.append(annualized_volatility)

    return np.array(returns), np.array(risks)

# 计算马科维茨最优组合
def calculate_optimal_portfolio(returns, risks):
    n_assets = len(returns)
    num_portfolios = 3000

    results = np.zeros((4, num_portfolios), dtype=object) 


    for i in range(num_portfolios):
        weights = np.random.random(n_assets)
        weights /= np.sum(weights)

        portfolio_return = np.sum(returns * weights)
        portfolio_risk = np.sqrt(np.dot(weights.T, np.dot(np.cov(returns, rowvar=False), weights)))

        results[0, i] = portfolio_return
        results[1, i] = portfolio_risk
        results[2, i] = portfolio_return / portfolio_risk
        results[3, i] = list(weights) # 将权重转换为列表

    return results

symbols = ['BTCUSDT','ETHUSDT', 'BNBUSDT','LINKUSDT','BCHUSDT','LTCUSDT']
data = get_data(symbols)

returns, risks = calculate_returns_risk(data)
optimal_portfolios = calculate_optimal_portfolio(returns, risks)

max_sharpe_idx = np.argmax(optimal_portfolios[2])
optimal_return = optimal_portfolios[0, max_sharpe_idx]
optimal_risk = optimal_portfolios[1, max_sharpe_idx]
optimal_weights = optimal_portfolios[3, max_sharpe_idx]

# 输出结果
print("最优组合:")
for i in range(len(symbols)):
    print(f"{symbols[i]}权重: {optimal_weights[i]:.4f}")

print(f"预期收益率: {optimal_return:.4f}")
print(f"预期风险(标准差): {optimal_risk:.4f}")
print(f"夏普比率: {optimal_return / optimal_risk:.4f}")

# 可视化投资组合
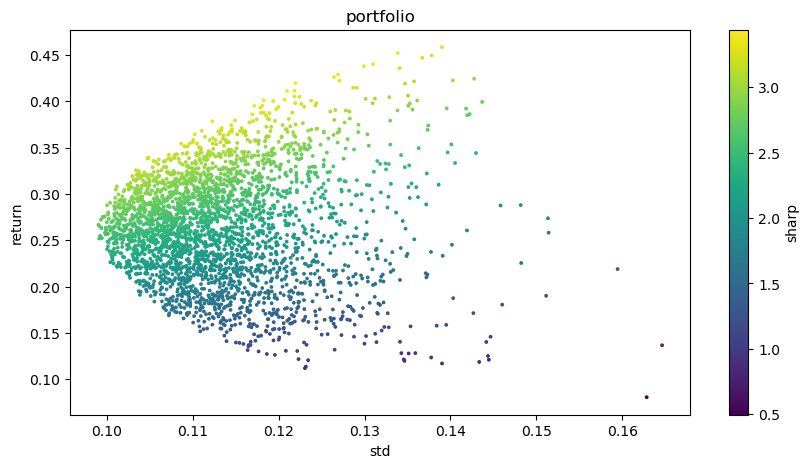
plt.figure(figsize=(10, 5))
plt.scatter(optimal_portfolios[1], optimal_portfolios[0], c=optimal_portfolios[2], marker='o', s=3)
plt.title('portfolio')
plt.xlabel('std')
plt.ylabel('return')
plt.colorbar(label='sharp')
plt.show()

最終出力:
最適な組み合わせ:
BTCUSDT ウェイト: 0.0721
ETHUSDT ウェイト: 0.2704
BNBUSDT ウェイト: 0.3646
LINKUSDT ウェイト: 0.1892
BCHUSDT 重み: 0.0829
LTCUSDT ウェイト: 0.0209
期待収益: 0.4195
期待リスク（標準偏差）：0.1219
シャープレシオ: 3.4403