ベイズ統計は、金融、医療研究、情報技術など、多くの分野で幅広く応用されている数学の強力な分野です。これにより、事前の信念と証拠を組み合わせて新たな事後的な信念に到達し、より情報に基づいた意思決定を行うことができます。

この記事では、この分野を創始した主要な数学者の一部を簡単に紹介します。

ベイズ以前 ベイズ統計をよりよく理解するには、18世紀に遡って数学者ド・モアブルと彼の論文「偶然の原理」を参照する必要があります。[1]。

ド・モアブルは論文の中で、当時の確率とギャンブルに関する多くの問題を取り上げました。ご存知のとおり、これらの問題の 1 つに対する彼の解決法が正規分布の起源につながりましたが、それはまた別の話です。

彼の論文には、次のような単純な疑問がある。

「公平なコインを3回続けて投げたときに、3回とも表が出る可能性。」

「偶然の原理」で説明されている問題を読むと、ほとんどの問題が、特定のイベントの確率を計算する仮説から始まることに気付くでしょう。たとえば、上記の問題では、コインが公平であるという仮定があるため、コインを投げて表が出る可能性は 0.5 です。

これは今日では数学的に次のように表現されます。

𝑃(𝑋|𝜃)

しかし、コインが公平かどうかわからない場合はどうなるでしょうか?知らなければ𝜃ウールの布？

トーマス・ベイズとリチャード・プライス

ほぼ50年後の1763年に、「偶然の原理に関する論文」と題する論文が発表された。[2] ロンドン王立協会の哲学論文集に掲載。

文書の最初の数ページには、数学者リチャード・プライスが書いた文章があり、友人のトーマス・ベイズが亡くなる数年前に書いた論文の内容を要約している。序文でプライスは、ド・モアブルの『偶然性の原理』では取り上げられなかったトーマス・ベイズによるいくつかの発見の重要性について説明しています。

実際、彼は具体的な問題について言及していました。

「未知のイベントの発生回数と失敗回数が与えられた場合、そのイベントの発生確率が任意の 2 つの確率の度合いの間にあるかどうかを調べます。」

言い換えれば、イベントを観察した後に、未知のパラメータを見つける。θ2 つの確率度間の確率はどれくらいですか?これは実際には統計的推論に関連する歴史上最初の問題の 1 つであり、逆確率という名前が付けられました。数学的に言えば：

𝑃( 𝜃 | 𝑋）

これはもちろん、今日私たちがベイズの定理の事後分布と呼んでいるものです。

原因不明の原因

この二人の年長牧師について知りましょう。トーマス・ベイズそしてリチャード・プライス研究の動機が実は非常に興味深いのです。しかし、これを行うには、統計に関する知識を少し脇に置いておく必要があります。

18 世紀になり、確率は数学者にとってますます関心の高い分野になりつつあります。ド・モアブルやベルヌーイなどの数学者は、いくつかの出来事はある程度ランダムに起こるものの、それでも一定のルールに支配されていることを示しました。たとえば、サイコロを何度も振ると、6 回のうち 1 回は 6 が出ます。まるで偶然の運命を決める隠されたルールがあるかのようです。

さて、あなたがこの時代に生きる数学者であり、敬虔な信者であると想像してください。この隠されたルールが神とどのように関係しているかを知りたいと思うかもしれません。

これはまさにベイズとプライス自身が尋ねた質問です。彼らがこの問題を解決するために望んだ解決策は、「世界は知恵と知性の結果でなければならない」ということを証明することに直接適用でき、それによって最終的な原因としての神の存在の証拠を提供する。[2] - つまり、因果関係はないのです。

ラプラス

驚くべきことに、約2年後の1774年に、トーマス・ベイズの論文を読んでいなかったと思われるフランスの数学者ラプラスが、「事象の確率による事象の原因について」と題する論文を執筆しました。[3]は逆確率問題に関する論文です。最初のページでは

主な原則:

「ある出来事がn個の異なる原因によって引き起こされる場合、特定の出来事に対するこれらの原因の確率は、その原因が与えられた場合の出来事の確率に等しい比率であり、これらの原因のそれぞれが存在する確率は等しい。原因を前提とした事象の確率。原因の確率を、それぞれの原因を前提とした事象の確率の合計で割ったもの。」

これは今日ベイズの定理として知られているものです。

​

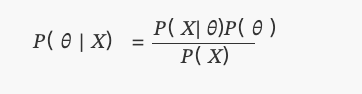
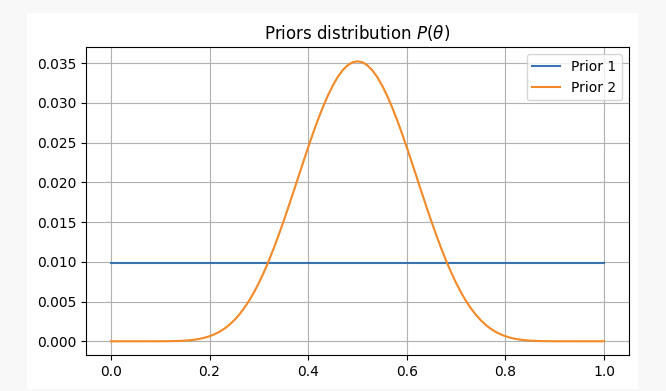
でP(θ)均一に分布しています。

コイン実験

Python と PyMC ライブラリを使用して簡単な実験を行うことで、ベイズ統計を現代に取り入れます。

友人があなたにコインを渡し、それが公平なコインだと思うかどうか尋ねたとします。彼は急いでいるので、コインを10回だけ投げるように言います。ご覧のとおり、この問題には未知のパラメータがありますpコイントスで表が出る確率を推定したい。pの最も可能性の高い値。

（注：パラメータについて話しているのではないpランダム変数ですが、このパラメータは固定されており、どの値の間になる可能性が最も高いかを知りたいのです。 ）

この問題に対する別の視点を得るために、次の 2 つの異なる前提に基づいてこの問題に取り組みます。

• 1. コインの公平性についての事前情報がなく、p。この場合、信念に何の情報も追加しないため、非情報事前確率と呼ばれるものを使用します。
• 1. コインが不公平であっても、それを非常に不公平にするのは難しいことを経験から知っているので、パラメータはpおそらく 0.3 を下回ったり 0.7 を超えたりすることはないでしょう。この場合、有益な事前情報を使用します。

どちらの場合も、私たちの事前の信念は次のようになります。

コインを10回投げると、2回表が出ます。この証拠があれば、パラメータがどこにあるかわかるだろうp？

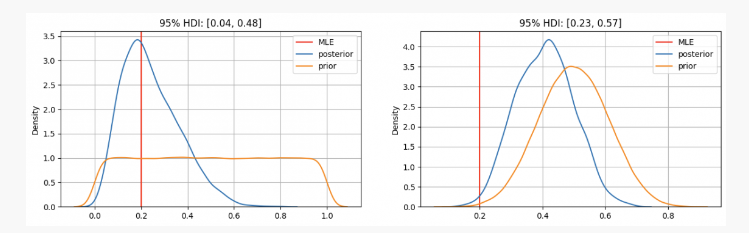
ご覧の通り、最初のケースではpの事前分布は最大尤度推定値（MLE）を中心とする。p=0.2これは頻度主義的方法を用いた同様のアプローチです。真の未知のパラメータは、0.04 から 0.48 までの 95% 信頼区間内にあります。

一方、パラメータがp 0.3 から 0.7 の間であるはずですが、事後分布は 0.4 前後であり、MLE によって与えられた値よりもはるかに高いことがわかります。この場合、真の未知のパラメータは、0.23 から 0.57 までの 95% 信頼区間内になります。

したがって、最初のケースでは、コインが不公平であると確信していることを友人に伝えることになります。しかし、別の場合には、コインが公平かどうかわからないと伝えるでしょう。

ご覧のとおり、同じ証拠（10 回投げて 2 回表）であっても、事前の信念が異なると結果が異なる場合があります。これはベイズ統計の強みであり、科学的方法と同様に、以前の信念を新しい観察や証拠と組み合わせることで信念を更新することができます。

END

今日の記事では、ベイズ統計の起源とその主な貢献者について見てきました。それ以来、この統計分野には多くの重要な貢献者がいました (Jeffreys、Cox、Shannon など)。quantdare.com から転載。