Smile Curve를 이용한 비트코인 ​​옵션의 델타 헤지

요약

우리는 암묵적 스마일 커브와 기타 스마일 조정 델타를 사용하여 비트코인 ​​옵션의 견고한 동적 델타 헤징을 분석합니다. 이러한 델타는 모든 규모 불변 확률적 및/또는 지역적 변동성 모델에 대해 동일하다는 의미에서 모델과 무관하거나 지역적 변동성의 간단한 체제 종속 매개변수화를 기반으로 합니다. 이러한 델타는 구현하기 쉽기 때문에 기존 자산에 대한 옵션 시장의 시장 조성자들에게 인기가 있습니다. 동적 델타 헤징에 대한 이전의 실증적 연구는 주식 지수 옵션에만 기반을 두었지만, 시간별 과거 비트코인 ​​옵션 가격에 대한 고유 데이터 분석 결과 비트코인의 내재 변동성 곡선의 행동은 주식 지수 옵션의 행동과 매우 다르다는 것을 보여줍니다. 광범위한 자금 조달 범위와 10일, 20일, 30일의 합성 고정 만기를 갖춘 콜 및 풋 옵션의 경우, 2개의 1년 기간에 걸쳐 다양한 스마일 조정 델타의 동적 헤지 성과를 비교합니다. 또한 우리는 헤지 수단으로 표준 선물보다는 영구 계약을 사용하는 것에 대해서도 조사합니다. 영구 계약의 기초 위험은 달력형 선물보다 훨씬 낮기 때문입니다. 결과는 헤지 오차 분산 비율의 검증 가능한 통계로 표현됩니다. 특정 기간 동안 암묵적 스마일 커브 헤지 비율을 사용하면 특히 영구 스왑을 헤지 도구로 사용할 때 단순한 블랙-숄스 델타 헤지보다 상당히 더 나은 성과를 낼 수 있으며, 외가격 풋 옵션의 효율성 이득은 30%를 초과할 수 있습니다. 상승하는 내재 변동성 곡선 기간 동안 단기 외가격 콜 옵션을 헤지할 경우, 평균 효율성 이득은 15%에 도달할 수 있습니다. 2021년에는 무기한 계약을 활용하는 이점이 특히 두드러지는데, 특히 기반이 여전히 상당히 큰 장기 계약의 경우 더욱 그렇습니다.

키워드 ：파생상품 헤지, 내재변동성 곡선, 영구계약, 견고한 자금조달, 역동적 증분 헤지

1. 서론

동적 델타 헤징에 관한 모든 연구는 Black과 Scholes(1973) 모델을 기반으로 합니다. 블랙-숄즈(BS) 델타는 기초 가격과 변동성 간의 상관 관계가 0이라고 가정하기 때문에 기초 가격에 대한 모델 옵션 가격의 편미분만 필요합니다. 그러나 주가 지수 옵션은 가격-변동성 상관관계가 크고 음의 값을 가지며, 이로 인해 내재 변동성 곡선이 상당히 왜곡된다는 것은 잘 알려진 사실입니다. Bates(2005)의 기본 아이디어와 Alexander 및 Nogueira(2007a)의 보다 일반적인 결과에 따라 암시적 변동성 곡선의 기울기는 모델에 구애받지 않는 BS 델타에 대한 조정을 암시하는 데 사용될 수 있습니다. 이는 모든 규모에 대해 일정하며 변형 모델은 동일합니다. 그러나 Alexander와 Nogueira(2007b)는 거래 가능한 상품(이자율 제외)의 경우 모든 확률론적 및/또는 지역적 변동성 주식 옵션 가격 책정 모델은 점프나 Lévy 프로세스와 같은 추가 요인에 관계없이 규모 불변이어야 함을 보여줍니다. 얼마나 복잡한가 특징은 다음과 같습니다. 따라서 두 매개변수 변동성 모델(거래 가능한 금융 상품에 대한)의 실증적 헤지 성과 간의 차이는 단순히 모델 간의 보정 오차가 다르기 때문에 발생합니다. 거래 가능한 금융 상품의 가격에 대한 옵션 가격의 델타(실제로는 감마) 편미분은 이론적으로 모형으로부터 자유로운 규모 불변 델타와 정확히 동일합니다. 주 1 또한, 베이츠(Bates, 2005)가 제안한 단순 스케일 불변량 델타(Simple Scale-Invariant Delta)는 스마일 곡선의 기울기가 음(-)일 때 BS 델타(BS Delta)보다 크다(작다). Coleman et al. (2001)은 BS 델타가 지역적 변동성 프레임워크에서 과도하게 헤지되는 경향이 있음을 보여주었기 때문에 암묵적 변동성이 음으로 왜곡되면 규모 불변 델타가 BS 델타보다 과도하게 헤지될 것입니다.

Alexander와 Nogueira(2007a)가 설명한 대로 가격에 대한 최소 분산(MV) 총 파생 상품은 0이 아닌 가격-변동성 상관 관계를 고려하는 또 다른 델타이지만 모델에 따라 달라집니다. 그러나 이 저자들은 Lee(2001)의 모델 없는 MV Delta를 사용하여 얻은 경험적 결과와 다른 스케일 불변 모델을 기반으로 한 MV Delta를 구별하지 못했습니다. Lee(2001)의 MV Delta도 “스마일 조정”되어 있습니다. 즉, 암시적 변동성 스마일 곡선의 경험적 특성을 사용하여 보정된 항을 BS 델타에 추가합니다. BS 델타를 조정하는 또 다른 방법은 Derman과 Kani(1994) 및 Derman(1999)이 제안한 Smile-Adjusted Delta의 선구적 연구에서 제안한 접근 방식을 사용하여 가격-변동성 상관관계를 포착하는 항을 추가하는 것입니다. 이것들은 완전히 모델에서 자유롭지 못합니다. 왜냐하면 조정 조건이 지역적 변동성의 매개변수화에 따라 달라지고, 지역적 변동성 자체가 시장의 지배적인 체제에 따라 달라지기 때문입니다. 그러나 기초 가격의 진화를 주도하는 프로세스(예: 확률적 지역 변동성 점프 확산)에 대한 가정이 없고 옵션 가격 및/또는 기초 과거 기록을 사용하여 보정해야 하는 매개변수가 없다는 점에서 모델이 없습니다. 데이터.

주식 옵션 시장 제작자가 BS 델타에 대한 간단한 모델 없는 조정을 사용하여 노출을 헤지하는 것은 표준 관행입니다. 이는 소위 “강력한 자금 조달”로 간주되기 때문입니다. 즉, 헤지 비율은 모델과 독립적입니다. 암묵적 미소 곡선과 미소에 맞춰 조정된 곡선 조정 델타 헤지는 의사들 사이에서 특히 인기가 많습니다. 이는 수많은 기사와 포럼에서 입증되었습니다. 참고 사항 2: 암묵적 스마일 커브 및/또는 스마일 조정 커브의 델타 헤지에 관한 실증적 연구가 이전에 여러 건 있었지만, 이들 모두는 주식 지수 옵션을 연구했습니다. 모든 결과가 일관적이지는 않습니다. Vähämaa(2004)는 일부 미소 곡선 조정 델타가 FTSE 100 옵션의 경우 BS 델타보다 성과가 더 좋지만 변동성이 과도한 기간 동안에만 그렇다는 것을 보여줍니다. Crépey(2004)는 이러한 결과가 DAX 30 옵션에도 적용된다는 것을 확인합니다. Attie( 2017)은 미소 암시 델타가 S&P 500 지수 옵션 헤지에서 BS 델타보다 지속적으로 더 우수한 성과를 보인다고 주장합니다. Alexander et al. (2012)은 Derman(1999)의 프레임워크를 Markov 스위칭 설정으로 확장하여 현재에 적용할 수 있는 올바른 미소 조정 델타를 반영합니다. 시장 체제에 따르면 S&P 500 옵션의 경우 BS 델타는 이 마르코프 스위칭 확장을 사용해야만 개선될 수 있습니다. François와 Stentoft(2021)도 S&P 500 지수 옵션을 연구했으며 표준 조정이 BS 델타 또는 델타 감마보다 성과가 좋을 수 없음을 확인했습니다. 헤지이지만, 새로운 암시적 미소 곡선 델타-감마-베가 헤지는 BS 모델을 크게 개선합니다. 다른 유형의 옵션과 관련해 스마일 조정 델타 헤징의 성공 여부에 대해서는 알려진 바가 거의 없습니다. 노트3

본 논문의 목적은 비트코인 ​​옵션에 적용된 다양한 Smile-implied curves와 기타 Smile-adjusted curves의 델타 헤지 성과를 조사하는 것입니다. 이 글을 쓰는 시점에서는 비트코인 ​​옵션에 관한 연구 자료가 극히 적습니다. Siu와 Elliott(2021), Jalan et al.(2021), Chen과 Huang(2021)은 모두 확률적 변동성 가격 책정 모델의 실증적 응용을 연구했지만, 어떤 논문도 헤지 성과를 연구하지 않았습니다. Hou et al. (2020)은 비트코인 ​​옵션의 가격을 책정하기 위해 일련의 확률적 변동성 모델을 고려했습니다. 저자들은 점프와 공동 점프의 중요성을 강조하는 일련의 중요한 결과를 제시하고 비트코인 ​​옵션의 가격을 매기기 위해 상관관계 점프(SVCJ)를 적용한 확률적 변동성 모델을 제안합니다. 이러한 모델은 클리킷이나 래칫 옵션과 같은 이국적인 옵션의 가격을 책정하는 데 매우 유용합니다. Chi와 Hao(2021)는 GARCH 기반 델타 헤지 전략을 고려하지만, 그들의 연구는 다양한 실현된 변동성 예측 모델을 비교하는 데 중점을 두고 있습니다. Alexander et al. (2022b)은 비트코인 ​​옵션의 내재적 변동성 스마일 곡선의 행동을 연구하여 시장 조성자 수요 압력이 방향성 트레이더 또는 변동성 트레이더에 의해 발생하는지 추론했습니다. 사실, 우리가 아는 한 비트코인 ​​옵션 헤지와 관련된 세부적인 연구는 단 하나뿐입니다(Matic et al., 2021). 그 연구는 본 논문과는 완전히 다른 접근 방식을 사용합니다. Matic et al. (2021)은 Deribit 거래소에서 인용한 일일 내재 변동성을 사용하여 매개 변수 확률 변동성에서 영감을 얻은 내재 변동성 표면을 보정한 다음, 1개월에서 3개월 사이의 옵션 내재 변동성을 중재 없는 방식으로 보간합니다. 변동성. 2019년 4월부터 2020년 3월까지의 샘플은 Duffie et al.(2000)과 McNeil 및 Frey(2000)가 도입한 확률적 변동성 프로세스를 사용하여 3개의 하위 기간(강세장, 평온한 시장, COVID 기간)으로 구분됩니다. GARCH 필터 커널 밀도를 사용하여 기본 암호화폐 가격을 모델링합니다. 그런 다음 그들은 BS 그리스의 헤지 성과를 다양한 확률적 변동성 점프 확산 모델에서 얻은 성과와 비교합니다. 연구자들은 1개월 만료 옵션의 경우 단순 BS 헤지에 비해 상당한 개선이 없다는 것을 발견했지만, 3개월 만료 옵션의 경우 보다 복잡한 모델이 헤지 성과를 상당히 개선했습니다.

Matic et al. (2021)과 달리 우리는 다양한 확률적 변동성 모델의 옵션 헤지 성과를 비교하지 않습니다. 우리 연구의 중요한 실질적 장점은 모든 델타 값을 계산하기가 매우 쉽다는 것입니다. 모든 정보는 모델에 의존하지 않는 직접적이고 견고한 방식으로 변동성 스마일 곡선에서 파생되므로 모델 보정이 필요하지 않습니다. 현재 시장 상황, 암묵적 변동성 스마일 모양 및/또는 가격-변동성 상관관계에 따라 다양한 BS 델타 조정을 사용하여 델타 헤지 결과를 도출해냈습니다.

저희는 만기가 10~30일인 단기 옵션에 초점을 맞추고 있습니다. 이는 Matic et al. (2021)에서 연구한 옵션보다 유동성이 훨씬 높고 행사 가격 범위가 더 넓습니다. 우리가 이렇게 하기로 한 이유는 만기일이 1개월에서 3개월 사이인 비트코인 ​​옵션은 전체 거래량의 20%에 불과하고, 만기일이 30일 이하인 옵션은 전체 거래량의 50%를 차지하기 때문입니다. 전체의 약 80% 거래량 더욱이 BS 델타를 미소에 맞게 조정하기 위해서는 적절한 미소 곡선이 필요하며, 이러한 단기 옵션의 액체 타격 범위는 매우 큽니다. 실제로 우리의 실증적 분석에 사용된 옵션의 화폐성 범위는 0.7에서 1.3 사이입니다.

우리는 자금 조달 시간 8시간마다 또는 UTC 기준 매일 00:00에 이루어지는 정기적 리밸런싱을 통한 동적 델타 헤징만 살펴봅니다. 이러한 실험 설계는 비트코인 ​​옵션 시장의 특성에 따른 것인데, 이는 참신하기 때문에 나중에 자세히 설명하겠습니다. 선물의 거래 비용은 옵션의 거래 비용보다 훨씬 적습니다. 예를 들어, 선물 계약은 만료 날짜에 따라 약 1~5베이시스포인트의 스프레드를 갖지만 감마 헤지에 자주 사용되는 단기 등가격 옵션은 일반적으로 약 200~300베이시스의 스프레드를 갖습니다. 전철기. 따라서 감마 헤징은 일반적인 동적 델타 헤징보다 훨씬 더 비쌉니다. 감마 헤지를 재조정하는 데 드는 거래 비용은 헤지 오류를 줄임으로써 얻은 이익을 잠식할 수 있는 반면, 델타 헤지를 재조정하는 데 드는 거래 비용은 적으며, 특히 영구 계약을 헤지 수단으로 사용하는 경우 더욱 그렇습니다.

다음으로, 섹션 2에서는 비트코인 ​​옵션과 선물 시장을 설명합니다. 섹션 3에서는 비트코인과 주가 지수의 내재 변동성 표면의 특성을 비교하고 그 특징을 구분합니다. 섹션 4에서는 우리의 경험적 프레임워크를 설명합니다. 각 헤지 비율은 조정된 BS 공식으로 소개됩니다. ; 섹션 5에서는 데이터를 설명하고, 섹션 6에서는 실증적 결과를 제시하며, 섹션 7에서 결론을 내립니다.

2. 비트코인 ​​옵션 및 선물 시장

이 글을 쓸 당시, 주요 암호화폐 거래소 6곳에서 비트코인과 기타 통화, 그리고 일부 토큰에 대한 옵션 거래를 제공하였고, 2021년 12월 총 일일 평균 거래량은 10억 달러에 달했습니다. 특히 비트코인 ​​옵션 거래량은 최근 역대 최고치를 경신했으며, 2020년 1월부터 2021년 12월까지 월평균 거래량이 2배 이상 늘었고 미결제 약정은 6배 이상 증가했습니다. 대부분의 거래는 Deribit 옵션 거래소에서 이뤄지는데, 이 거래소는 미국 상품선물거래위원회(CFTC) 등 정부 기관이 정한 국제 표준을 따르지 않고 고객 이익을 보호하기 위한 기타 규제를 피하기 위해 파나마로 이전했습니다. 다른 많은 규제되지 않은 암호화폐 파생상품 거래소와 마찬가지로, 종종 해외 조세 피난처에 등록되어 있는 Deribit의 거래 플랫폼은 24시간 연중무휴로 운영되며 “고객을 아는 것”에 관한 프로토콜을 거의 또는 전혀 준수하지 않습니다. 2020년에는 Deribit에서 430만 건의 계약(명목 가치 약 550억 달러)이 거래되었고, 2021년에는 620만 건의 계약(명목 가치 약 2,900억 달러)이 거래되었습니다. 그 결과, 단 2년 만에 상장 계약 수가 45% 이상 늘어났고, Deribit에서 거래된 명목 금액은 430% 이상 증가했습니다. 참고 4 이를 좀 더 구체적으로 설명하자면, 시카고 옵션 거래소(CBOE) S&P 500 옵션 시장은 2020년에서 2021년 사이에 약 10%만 성장했습니다. 참고 5 비트코인 ​​옵션 시장에서는 새로운 계약 규모, 더 넓은 행사 가격 범위, 더 긴 만기, 새로운 기초 자산이 거의 매달 출시되어 이 새로운 파생 상품 시장이 소매 및 기관 거래자 모두에게 확대됩니다. 비트코인 ​​옵션이 더 이상 틈새 시장 제품이 아닙니다. . 2022년 3월, 시카고 상품거래소(CME)는 소매 투자자를 대상으로 하는 자체 규제 플랫폼과 경쟁하기 위해 마이크로 비트코인 ​​옵션을 출시했습니다. 하지만 대형 기관 플레이어들도 옵션 시장을 매우 주의 깊게 지켜보고 있으며, 일부는 이를 “다음 큰 단계”라고 부르기도 합니다. 참고 6 반면, Opyn이나 Ribbon Finance와 같은 새로운 분산형 금융(DeFi) 프로토콜은 규정을 전혀 준수하지 않고도 옵션 거래를 제공합니다. 하루 가상 거래량이 5억 달러가 넘는 이 시장은 더 이상 전통적인 투자자가 무시할 수 없는 시장이 되었습니다.

Deribit의 거래량은 엄청나서 모든 유형의 암호화폐 옵션 연구에 가장 매력적인 거래소입니다. CME(및 일부 다른 거래소)는 비트코인 ​​옵션만 상장하지만, 비트코인 ​​옵션 거래량의 10~15%만이 이러한 거래소에서 거래됩니다. 데리비트 하나만 해도 비트코인 ​​옵션 거래량의 90% 이상을 차지합니다. 참고 7 한 가지 이유는 Deribit이 주중 24시간 운영되는 반면 CME는 주중에만 운영되기 때문일 수 있습니다. 또 다른 이유는 Deribit 옵션의 기초 자산이 BTC 지수의 USD 가치임에도 불구하고 증거금이 적용되고 비트코인으로 결제되기 때문일 수 있습니다. 만기 지급금을 얻으려면 USD로 표시된 BTC 가치와 옵션 행사 가격(역시 USD로 표시)의 차이를 계산하고 그 결과를 만기 시점의 BTC 지수 가치를 사용하여 비트코인으로 변환합니다. 참고 사항 8 결제 가격(예: 비트코인)과 기초 자산(예: USD) 간의 통화 단위 차이는 반대 방향으로 선물이나 옵션이 없다는 점을 제외하면 콴토 FX 옵션의 수익과 매우 유사합니다. 즉, 비트코인 ​​1달러의 가치에 기반한 파생상품은 없고, 비트코인 ​​1달러의 가치를 기초 자산으로 사용하는 옵션도 없습니다. 이러한 이유로 비트코인 ​​옵션은 “역옵션”이라고 불리며, 사실 이는 많은 암호화폐 파생상품 거래소에서 활발하게 거래되는 역선물을 포함한 여러 역파생상품 중 하나일 뿐입니다. 법정 통화-암호화폐 교차 파생상품 거래는 증거금 계좌나 계약 결제에 법정 통화를 담보로 사용하지 않고도 수행할 수 있기 때문에 매력적입니다.

비트코인이 전통적인 의미의 금융 시장으로 존재할 수 있는지는 논란의 여지가 있지만(Sauer, 2016), 비트코인(그리고 다른 통화와 토큰)을 위한 매우 활성화된 분산형 금융 시장은 많은 Farming 사이트와 다양한 유동성 풀에 존재합니다. 참고 사항 9 따라서 USD에서 비트코인으로 변환하여 USD로 표시된 모델의 헤지 효과를 측정할 수 있습니다.

어떤 헤지 방법을 선택하든 헤지 자체는 간단합니다. 거래자는 옵션에 대한 포지션을 열고 기초 자산에 대해 옵션의 델타 값과 동일한 포지션 크기로 반대 포지션을 취합니다. 전통적인 시장에서 헤지 수단은 일반적으로 옵션과 동일한 만기를 가진 선물 계약입니다. 결제 가격이 쉽게 거래될 수 있는 수단이 아니기 때문입니다. BTC 지수의 경우, 여러 거래소의 비트코인 ​​가격 평균을 기준으로 하므로 동일한 설명이 적용됩니다. 하지만 이는 헤지 수단이 반드시 옵션과 동일한 만기를 가진 역방향 선물 계약이어야 한다는 것을 의미하지는 않습니다. 비트코인에서 거래 가능한 헤지 수단을 선택하는 데에는 몇 가지 혁신적인 대안이 있기 때문입니다. 첫째, 3가지 유형의 유한일 선물 계약이 있습니다. 표준 선형 선물은 기존 자산 클래스에 대한 선물과 다르지 않습니다. 스테이블코인(예: 테더)에 대한 비트코인 ​​선형 선물은 스테이블코인 가격이 변동할 때마다 거래됩니다. USD 페그에서 시작하여, 기본 위험이 도입되고, USD 선형 선물과 유사한 속성을 지니지만 암호화폐처럼 증거금이 있고 결제되는 역 선물이 있습니다. 노트 10

비트코인 옵션에는 암호화폐 시장에서만 찾아볼 수 있는 계약을 활용하는 헤지 도구도 있습니다. 이러한 계약은 종종 영구 선물 또는 영구 스왑, 또는 간단히 “영구 계약”이라고 불리며, 이는 지금까지 가장 인기 있는 암호화폐 파생상품 유형입니다. 이들의 가격은 현물 가격과 긴밀하게 연계되어 있으며, 8시간마다 순 포지션의 일부를 자동으로 지급하거나 받는 “펀딩” 메커니즘을 사용합니다. “자금 조달 비율”이라고 하는 이 비율의 계산 방식은 거래소마다 다릅니다. 참고사항 11 지불인과 수령인은 영구 계약 가격이 현물(BTC) 가격보다 높은지 낮은지에 따라 달라집니다. 무기한 계약 가격이 현물 가격보다 높으면 자금 조달 비율은 양수이고 장기 무기한 계약 포지션을 보유한 사용자는 수수료를 지불해야 하는 반면, 단기 포지션을 보유한 사용자는 수수료를 받습니다. 현물 가격보다 영구 계약 가격이 낮으면 그 반대가 적용됩니다. 롱 포지션과 숏 포지션 간의 정기적인 자금 조달 지급으로 인해 영구 계약 가격은 현물 가격과 매우 가깝게 유지됩니다.

세계 최대의 암호화폐 현물 및 파생상품 거래소인 바이낸스에서 거래 상품의 3분의 2가 영구 선물 계약입니다. CryptoCompare(2022) 보고서에서 알 수 있듯이 현물과 파생상품 간의 이러한 비율은 암호화폐 시장에서 표준으로 여겨집니다. 이 글을 쓰는 시점에서 8개의 암호화폐 거래소가 일일 평균 선물 거래량이 10억 달러를 초과했다고 보고했으며, 그 중 대부분은 무기한 계약에서 나왔습니다. 참고 12 여기서 바이낸스, OKEx, 바이비트 등 규제되지 않은 거래소가 전체 선물 거래의 65% 이상을 차지합니다. 대조적으로, 규제된 거래소, 특히 CME와 FTX US의 시장 점유율은 약 25%로 훨씬 낮습니다. Deribit 선물의 일일 평균 거래량은 40억 달러가 넘으며, 이를 통해 이 선물을 적합한 헤지 수단으로 고려할 수 있을 만큼 충분한 유동성을 제공합니다. 하지만 다른 거래소와 마찬가지로 대부분의 거래는 달력형 선물보다는 영구 계약으로 이루어집니다. 이를 확인하기 위해, 그림 1은 2020년 1월부터 시작하여 2년 동안 7일 이동평균을 사용하여 평활화한 이러한 계약의 명목 거래 금액을 매일 기록한 것입니다. 명백히, 영구 선물 계약은 유한 일자 선물 계약보다 거래량이 훨씬 많습니다. 다만, 후자의 경우 우리는 세 가지 유형의 선물 계약에 대한 일일 거래량 데이터와 각 만기일에 대한 데이터를 통합했습니다. 2021년에는 영구 선물 계약의 거래량이 전년 대비 거의 4배나 증가했습니다. 표 1은 이러한 거래량의 변화를 경험적으로 보여줍니다. 이는 데리비트 거래소에서 거래되는 3가지 주요 비트코인 ​​파생상품의 평균 일별 거래량과 미결제 약정을 보여줍니다. 2020년과 2021년 사이에 모든 상품의 거래량과 미결제 약정이 크게 증가했는데, 이는 주요 은행과 자기자본 거래 회사가 암호화폐 분야에 관심을 보인 데 따른 것으로 보입니다.

그림 1. Deribit 선물 및 무기한 계약의 평균 일별 거래량.

그림 1은 2020년 1월부터 2022년 1월까지의 영구 선물 계약의 평균 일별 거래량(파란색)과 다른 모든 선물 계약의 평균 총 거래량(빨간색)을 보여줍니다. 일일 거래량은 24시간 동안 Deribit에서 거래된 총 계약 수에 명목 가치 10달러를 곱한 다음 지난 7일 동안의 평균을 구하여 계산합니다. 결과는 수십억 달러에 달합니다.

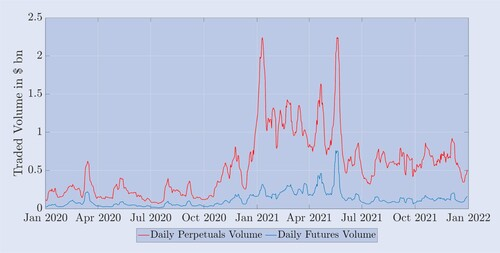
표 1. Deribit 비트코인 ​​파생상품의 거래량 및 미결제약정.

3. 비트코인의 암시적 변동성

그림 2는 Deribit 옵션에서 파생된 내재 변동성 곡선의 경험적 역학을 2년 반 동안의 일일 구조로 나타낸 것입니다. 화폐성 축은 외가격 콜 옵션에서 외가격 풋 옵션으로의 가격에 의해 암시되는 변동성 곡선을 나타내며, 여기서 깊은 외가격 풋 옵션의 화폐성은 0.7입니다. 딥 아웃 오브 더 머니 콜 옵션의 머니성은 1.3이고, 앳 더 머니 옵션의 머니성은 1.3입니다. 콜 옵션과 풋 옵션 모두 머니성은 1이고, 우리는 이러한 머니성 수준을 나타내기 위해 데이터를 보간합니다. 고정된 30일 만료 기간. 데이터와 필터링에 대한 자세한 내용은 다음 섹션에서 설명합니다.

그림 2. 비트코인 ​​내재 변동성 곡선.

2020년 1월 1일부터 2022년 6월 30일까지의 일일 데이터를 바탕으로 30일 일정 만기 기간을 갖는 비트코인 ​​옵션의 내재 변동성 곡선을 나타내며, 외가격 및 등가격 옵션에서 파생되었습니다. 행사 가격은 현재 기반 비트코인 ​​지수 가치보다 30% 낮거나 30% 높습니다.

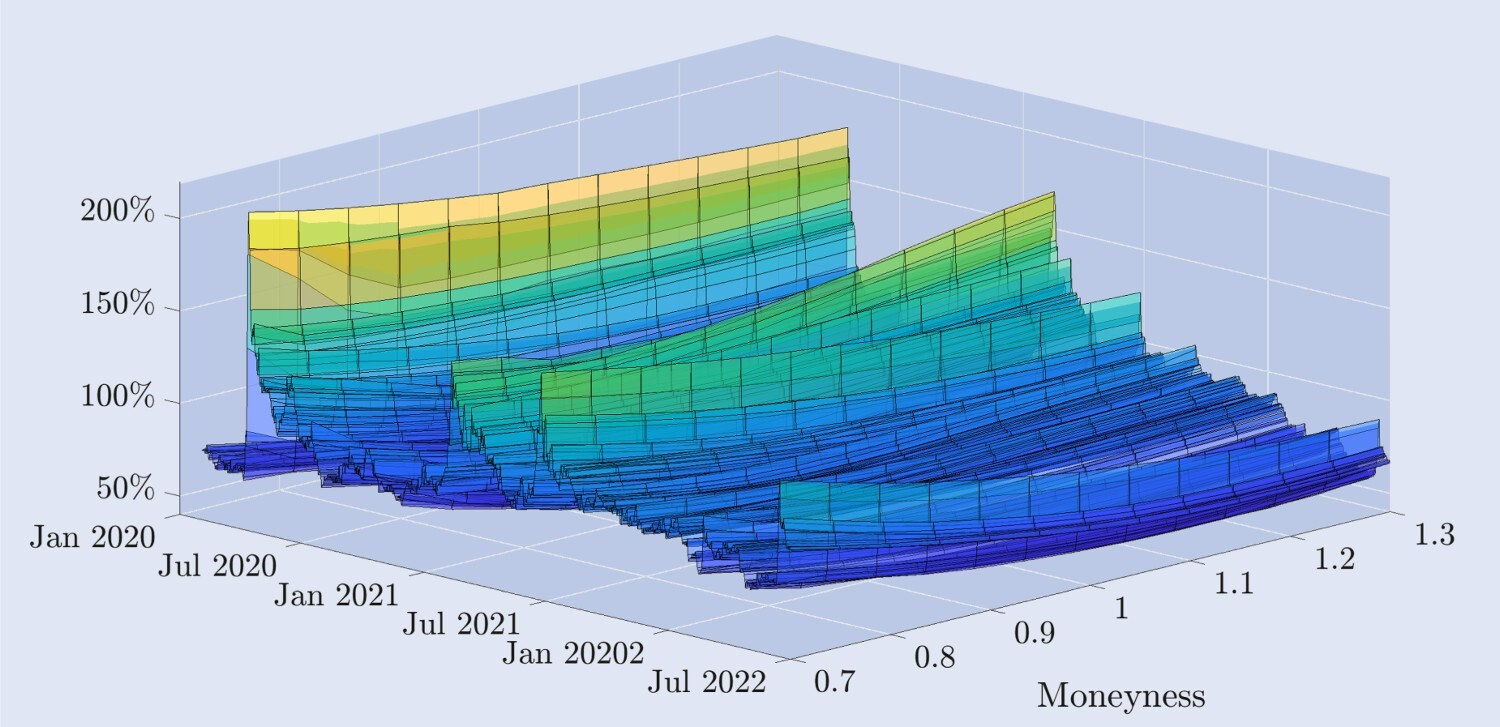
곡선의 모양은 시간이 지남에 따라 크게 달라집니다. 2020년 3월 “블랙 목요일” 사건 직후, 비트코인 ​​가격이 몇 시간 만에 30% 이상 하락했을 때, 내재 변동성 곡선은 주식 지수 옵션의 전형적인 부정적으로 왜곡된 모양을 띠었습니다. 즉, 외가격 풋 옵션의 변동성은 외가격 콜 옵션의 변동성보다 훨씬 높습니다. 그러나 일반적으로 비트코인 ​​옵션은 주가 지수 옵션보다 내재된 변동성이 훨씬 높습니다. 대부분의 샘플 기간 동안 암시적 변동성 곡선은 “하키 스틱” 모양을 보였지만, 특히 조용한 기간에는 약간 대칭적인 미소 모양으로 평평해졌습니다. 또한, 외가격 콜의 변동성이 외가격 풋의 변동성보다 훨씬 높은 양의 왜도가 나타나는 경우도 있습니다. 이러한 특징은 주식 지수 옵션 시장에서는 흔하지 않습니다. 이곳에서는 이를 설명하는 데 “스마일”이라는 용어 대신 “왜곡”이라는 용어가 더 많이 사용됩니다. 이러한 관점을 뒷받침하기 위해 그림 3은 암묵적 변동성 스마일의 또 다른 관점을 제공합니다. 이 차트는 다양한 통화 수준에서 비트코인의 내재적 변동성을 보여줍니다(위 차트). 또한 ATM 변동성과의 편차, 즉 고정 통화 변동성과 ATM 변동성의 차이(아래 차트)도 보여줍니다. 대부분의 샘플에서, 화폐성이 0.7인 외가격 풋 옵션이 가장 높은 내재 변동성을 갖습니다. 전통적인 (주식) 시장에서 이러한 엄청난 가격 하락 상태의 풋 옵션은 주가 하락에 대한 매력적인 보험입니다. 예를 들어, S&P 500의 경우, 내재 변동성 곡선의 뚜렷하고 거의 선형적으로 왜곡된 모양은 기초 자산의 하락 이후 가격이 가장 많이 오르는 옵션이 가장 화폐성이 낮다는 것을 의미합니다. 이와 대조적으로, 그림 3은 2020년 3월 12일 폭락 이전에 비트코인의 내재 변동성 곡선이 상대적으로 대칭적이었음을 보여줍니다. ATM 옵션은 약 50%로 가장 낮은 변동성을 갖는 반면, 외가격 풋과 외가격 콜은 거의 같은 변동성을 갖지만 둘 다 더 높으며, 외가격 변동성은 0.7과 1.3 옵션입니다. 약 75%. 그러나 폭락 속에서 비대칭적 미소가 뚜렷하게 나타났으며, 위험을 회피하는 투자자들은 가격이 다시 급락할 경우를 대비해, 돈 없는 풋 옵션을 더 높은 프리미엄으로 매수했습니다. 30일 동안 가격이 크게 떨어진 풋 옵션의 내재 변동성이 갑자기 200%에 가깝게 뛰었습니다. 비트코인은 처음으로 뚜렷한 음의 왜곡을 보였지만, 그 모양은 일반적으로 주가 지수 옵션에서 관찰되는 왜곡된 모양에 비해 여전히 훨씬 평평한 모양입니다. 이러한 비대칭성은 지속되지만, 내재 변동성 수준이 감소함에 따라 내재 변동성 곡선의 모양은 다시 미소 모양을 띠기 시작합니다.

그림 3. 비트코인의 내재적 변동성과 ATM 편향.

그림은 2020년 1월 1일부터 2022년 6월 30일까지의 기간 30일의 비트코인 ​​옵션에 대한 내재 변동성 곡선을 보여줍니다. 곡선은 외가격 옵션과 등가격 옵션을 사용하여 계산되며, 행사 가격은 현재 비트코인 ​​지수의 30% 하락에서 30% 상승까지 다양합니다.

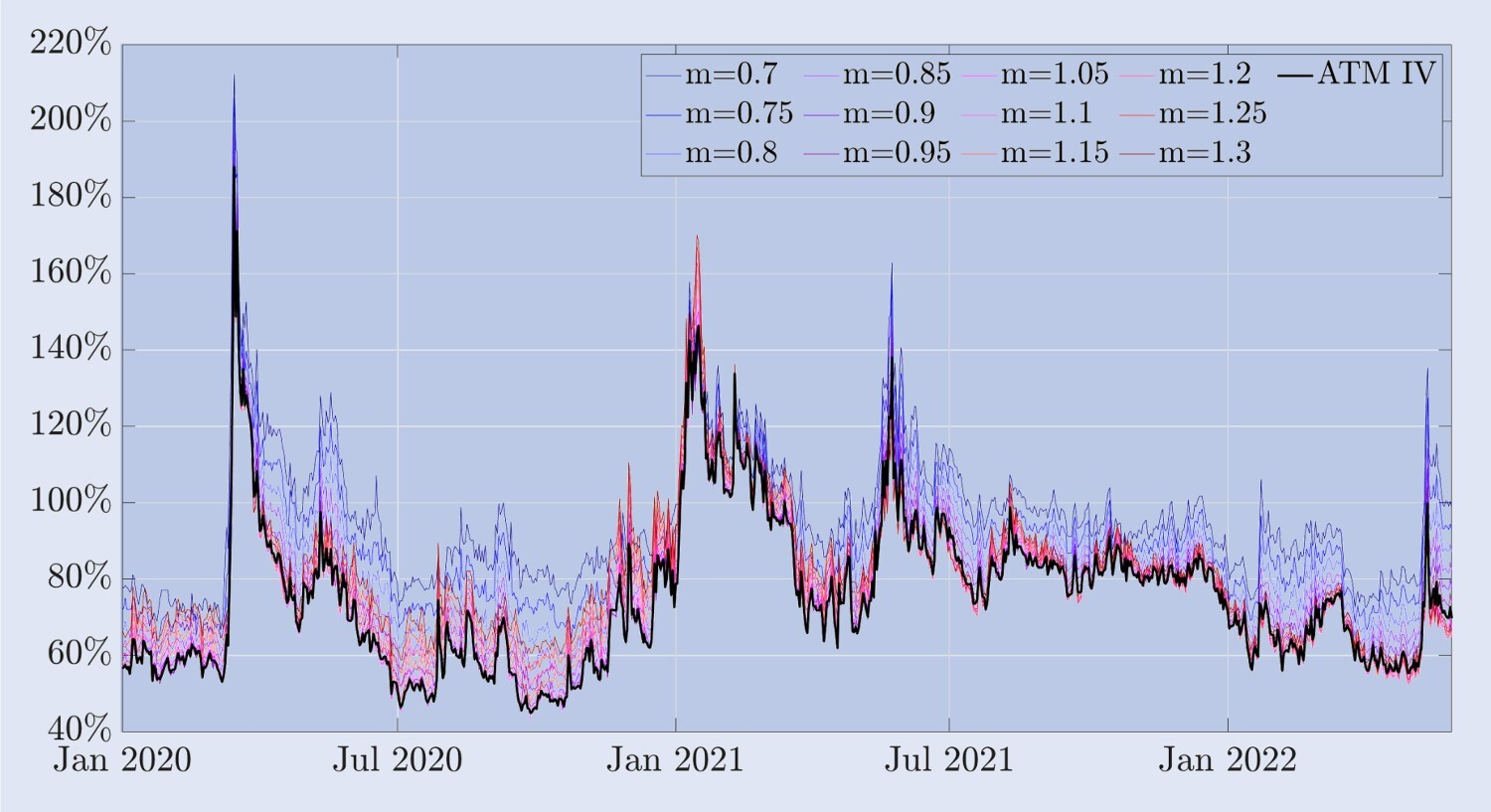
샘플 데이터에 따르면, ATM(at the money) 내재 변동성은 스마일 커브의 가장 낮은 지점인 것으로 보이며 대부분의 시간 동안 부정적으로 왜곡됩니다. 그러나 주식 지수 옵션과는 달리 스마일링 곡선은 변동성이 높은 기간 동안 상당한 양의 왜도를 보입니다. 예를 들어, 2021년 6월 비트코인 ​​랠리 동안 스마일 커브의 기울기가 증가했고 몇 달 동안 긍정적으로 왜곡된 상태를 유지했습니다. 주가 지수 가격과 변동성 간의 상관관계는 거의 항상 크고 부정적이지만, 비트코인 ​​가격과 내재된 변동성 간의 상관관계는 시장 상황에 따라 달라지는 것으로 보입니다. 2019년 8월부터 2020년 11월까지 비트코인 ​​가격과 30일 ATM 내재 변동성 간의 상관관계는 약 -0.42였으며, 다음 5개월 동안 상관관계는 0.74로 상승했습니다. 2022년 7월부터 2017년 11월까지 가격과 변동성은 0.08입니다.

그러나 일부 특성은 주가 지수 옵션의 내재 변동성과 유사합니다. (i) 다양한 가상성의 변동성은 그림 3에서 보여지는 것처럼 동일 만기의 등가격 변동성과 높은 상관관계를 갖습니다. (ii) 비트코인의 내재적 변동성은 변동성 기간 구조가 높은 변동성 역방향 선물과 비교적 변동성이 낮은 전방 선물 사이에서 규칙적인 변동을 보여줍니다. 그림 4는 주가 지수의 변동성 기간 구조와 유사하게 비트코인의 내재 변동성이 대부분의 역방향 선물 기간 동안 변동이 작고 유사한 추세를 보인다는 것을 보여줍니다.

그림 4. 비트코인의 암묵적 변동성 기간 구조.

2020년 1월 1일부터 2021년 12월 31일까지 10일, 20일, 30일 고정 만기일을 포함한 비트코인 ​​옵션의 내재 변동성 기간 구조는 등가격 옵션을 기준으로 계산되었습니다. 비교적 평온한 기간에는 기간 구조가 긍정적인 미래를 보여주는 반면, 폭락 기간(특히 2020년 3월과 2021년 6월)에는 그 반대가 사실입니다.

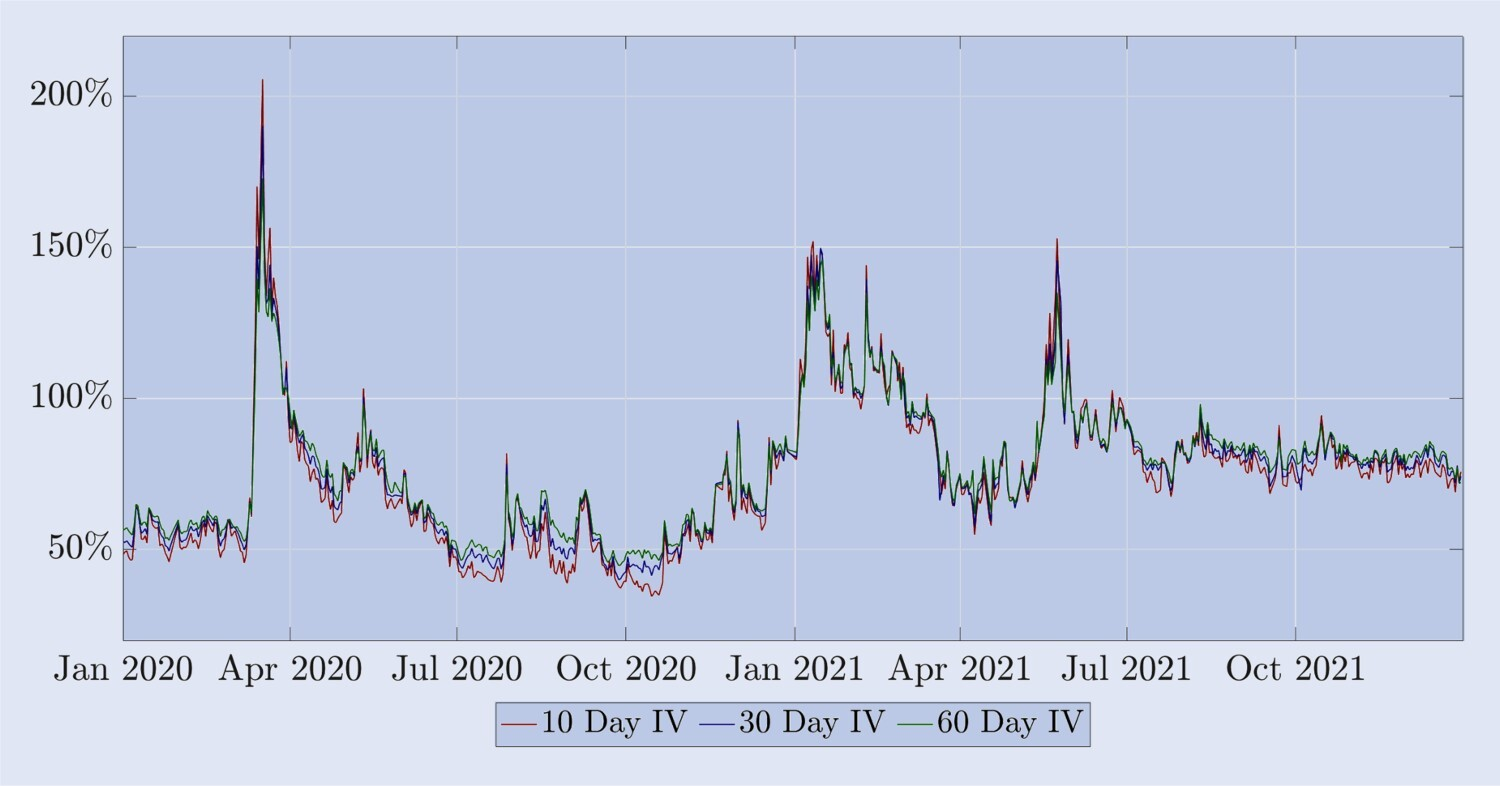
이 글의 나머지 부분에서는 위에서 강조한 비트코인 ​​옵션과 선물의 특징을 살펴보겠습니다. 장기적으로 비트코인을 보유하고 있는 사람은 가격이 크게 하락하는 경우를 대비해 외가격 풋 옵션을 매수하고 현물 포지션을 적절히 헤지하는 것을 고려할 수도 있습니다. 그러나 시장 조작자와 기타 전문 트레이더는 유동성 공급자로서 옵션 위험을 헤지하는 것이 중요하기 때문에 동적 델타 헤지 거래에 적극적으로 참여합니다. 이러한 헤지를 달성하기 위해 BS 델타를 사용할 수 있지만, 주식 옵션 거래자들 사이에서 스마일 커브 델타 조정이 널리 퍼져 있다는 점을 감안할 때, 비트코인 ​​옵션에 대한 이 델타의 효과를 조사하는 것은 흥미로울 것입니다. 우리는 주식 지수 옵션 헤지에서 스마일링 커브 조정 델타의 효과를 논하는 문헌을 검토하였고, 많은 경우 BS 델타가 스마일링 커브 조정 델타만큼 효과적임을 보여주었습니다. 그러나 비트코인 ​​옵션에 대해 이 문제를 탐구한 이전 연구는 없으며, 방금 논의한 비트코인 ​​내재 변동성 곡선의 매우 다른 동작과 비트코인에 사용할 수 있는 다양한 새로운 헤지 도구에서 알 수 있듯이 우리는 단순히 외삽할 수 없습니다. 비트코인 옵션 헤지거래에 대한 결론을 도출하기 위해 주가 지수 옵션에 대해 알려진 사항을 살펴보겠습니다. 따라서 본 연구의 목적은 헤지 수단의 선택에 따른 비트코인 ​​옵션의 헤지 오류의 표준편차를 최소화하는 데 있어 실무자들이 일반적으로 사용하는 다양한 스마일링 커브 조정 델타를 소개하고 비교하여 그 효과를 분석하는 것입니다. 사실, 이 연구는 옵션 거래 및/또는 헤지가 이루어지는 거래소 수준까지 확장될 수도 있습니다. 예를 들어, Deribit 거래소에 상장된 옵션을 헤지하려면 Binance나 Deribit 선물 상품을 사용하는 것이 더 낫을까요, 아니면 무기한 계약을 사용하는 것이 더 낫을까요? 하지만 이 연구에서는 비트코인 ​​옵션 헤지 문제의 세부적인 내용은 논의하지 않습니다. 적어도 현재 이 글을 쓰고 있는 시점에서는 Deribit 옵션 시장이 모든 비트코인 ​​옵션 거래량의 90% 이상을 차지하고 있으며, Deribit 옵션 시장 조성자들과의 개인적인 의사소통에 따르면 그들은 델타 헤지 활동에만 Deribit 선물 플랫폼을 사용한다고 합니다.

4. 헤지비율

우리의 실험 설계에서는 1비트코인 가치의 비트코인 ​​지수 선물에 대한 표준 유럽식 옵션을 작성하고 특정 수의 선물 계약에 대해 롱 포지션을 취하여 이를 헤지합니다. T만기 선물은 거래자가 현재 합의된 비트코인-USD 환율로 미래의 시간 T에 특정 양의 비트코인을 사거나 파는 계약을 맺을 수 있게 해줍니다. 선물 및 옵션의 기초 자산은 거래 불가능한 복합 지수인 Deribit Bitcoin Index BTC입니다. 하지만 T 만기 선물 계약 대신 무기한 계약 포지션을 통해 T 만기 옵션을 헤지할 수도 있습니다. 우리는 혼란을 일으키지 않고 표기법에서 실행 시간 t를 생략할 수 있으며, 행사 가격 K와 만기일 T를 갖는 역 옵션의 시간 t에서의 가격을 f(K,T|F,σ)로 표시합니다. 여기서 F는 다음과 같습니다. T 시점 t에서 만료되는 영구 가격 또는 선물 가격, σ:=σt(K,T|F)는 옵션의 내재 변동성을 나타내며, 이는 시점 t에서의 변동성이기도 합니다. 변동성과 기초 자산 간의 관계를 헤지 프레임워크에 통합하여, 체인 룰에 기반한 스마일 조정 델타 δadj, 즉 BS 델타보다 더 정확한 델타를 얻는 것을 목표로 합니다.

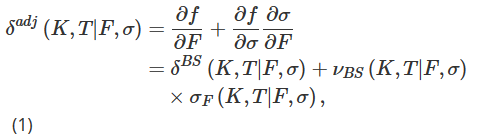
여기서 δBS는 표준 BS 델타이고, νBS는 BS 옵션 가격의 변동성 민감도(베가)이며, σF = ∂σ/∂F는 가격에 대한 변동성 민감도, 즉 기초 자산의 변화에 ​​따른 내재 변동성의 변화입니다… BS 델타와 베가는 공식이 폐쇄형이고 계산하기 쉽지만, σF를 정량화하는 것은 비교적 어렵고 다양한 방법이 있습니다.

우리가 논의한 BS 델타에 대한 첫 번째 조정은 시장의 현재 상태 또는 “시장 체제”에 따라 지역 변동성을 다르게 매개변수화하는 다양한 방법에 기인합니다. 지역 변동성의 개념은 Dupire(1994)와 Derman et al.(1996)의 고전적 논문을 시작으로 다양한 학술 문헌에서 발전되어 왔습니다. 여기서 특히 흥미로운 점은 Derman(1999)이 주식 지수 옵션 헤지와 관련하여 주창한 “스티키 모델”입니다. 이는 기초 자산 가격의 변화를 모델링하는 이진 트리의 노드에 서로 다른 지역 변동성 매개변수화를 적용합니다. Derman et al. (1996)은 σF를 행사가격에 대한 암묵적 변동성의 기울기로 근사화하도록 제안했습니다. 참고 13

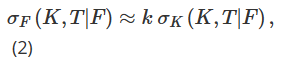
이 중 σK=∂σ/∂K는 행사가격에 대한 변동성의 미분을 나타내며, k는 현재 시장 메커니즘에 따라 달라져야 합니다. 실제로 Derman(1999)은 다양한 시장 체제 하에서 지역적 변동성 행동을 표현하기 위해 세 가지 다른 “점착성 모델”을 도입했습니다. 스티키 스트라이크 모델(SS)은 추세적인 시장 상황을 설명하고 변동성이 기초 자산의 미래 가격 움직임과 무관하며, BS 가정과 마찬가지로 일정하고 각 옵션에 대해 동일하다고 가정합니다. 이 메커니즘에서 델타는 BS 델타와 같습니다. 참고 사항 14 스티키 머니(SM)(때로는 스티키 델타라고도 함) 모델은 범위가 제한된 시장을 고려합니다. 이 메커니즘에 따르면, 옵션의 변동성은 통화성(또는 델타)에만 좌우됩니다. 따라서 지역적 변동성은 트리의 모든 노드에서 동일하지만, 각 옵션은 옵션의 가격성에 따라 다른 지역적 변동성을 갖는 서로 다른 트리를 갖습니다. 기초 자산의 가격이 변하면 옵션의 화폐성도 변하고, 옵션 가격을 책정하기 위해 다른 트리로 이동해야 합니다. 마지막으로, 스티키 트리 모델(ST)은 급격한 시장 하락 중에 나타나는 국부적 변동성 행동을 포착합니다. 즉, 변동성과 기초 자산 가격 사이에 강한 음의 상관관계가 있을 때 웃는 모양의 곡선 조정을 설명합니다. 이 숨겨진 트리 모델의 이름은 Derman과 Kani(1994)가 제안한 지역 변동성 모델에서 유래되었습니다. 마찬가지로, 지역적 변동성은 결정적 함수이지만, 트리의 각 노드에서 다를 수 있으며, 모든 옵션의 가격을 책정하는 데 동일한 트리가 사용됩니다. 이 세 가지 다른 유형의 지역 변동성 매개변수화에서 공식(2)의 k 값은 아래에 표시된 대로 시장 메커니즘에 따라 달라집니다.

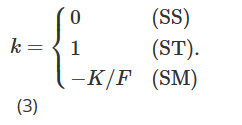
Crépey(2004)와 Alexander et al.(2012)은 모두 근사치(2)를 확장하여 k의 상태 의존성을 포함시켰습니다. 또한 Alexander et al. (2012)의 방정식 (1) 및 (2)를 Alexander 및 Nogueira (2007b)의 방정식 (3)과 결합하고 일부 대수 조작을 수행하면 Bates의 미소 곡선( 2005)는 암묵적으로 스케일 불변 델타(Alexander 및 Nogueira(2007a)에서 일반화됨)가 스티키 머니(SM) 근사치와 동일합니다.

비트코인의 높은 변동성을 고려하면 사용 가능한 행사 가격 범위는 시간이 지남에 따라 상당히 달라질 수 있습니다. 따라서 더 긴 기간 동안 동일한 특성을 가진 옵션을 연구하기 위한 프레임워크를 제공하기 위해, 우리는 행사 가격에서 가격 내 지표로 전환합니다. 우리는 화폐성 m을 m=K/F로 정의하고, 이제 암묵적 변동성을 나타내기 위해 θ(m,T|F)=σ(mK,T|F)를 사용합니다. θ(m,T|F)의 편미분을 F와 m에 대해 각각 θF(m,T|F)와 θm(m,T|F)로 표시하면 조정된 델타(7)를 다음과 같이 다시 쓸 수 있습니다.

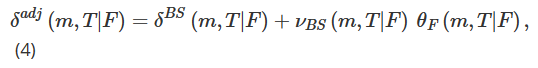
우리는 Derman(1999)이 제안한 지역 변동성 가설을 사용하여 변동성-가격 민감도 θF를 추정합니다. 옵션 가격 변화를 시뮬레이션하는 데 사용되는 트리 구조는 세 가지 가능한 시장 모델, 즉 안정 추세 시장(SS), 범위 시장(SM), 점프 폭락 시장(ST)에 따라 달라집니다. 따라서 Derman(1999)의 스티키델타를 화폐적 측정치로 환산하면 (5)의 κ 값은 시장모형에 따라 달라야 한다.

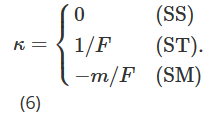
이전과 마찬가지로 Bates(2005)와 Alexander 및 Nogueira(2007a)가 제안한 모델 없는, 미소 암시적, 스케일 불변 델타는 Derman 및 Kani(1994)의 끈적끈적한 통화 측정(SM) 델타와 동일합니다.

다음으로 최소 분산(MV) 델타 δmv, 즉 델타 헤지 포트폴리오의 순간 분산을 최소화하는 델타를 고려합니다. 여기서 우리는 지역적 분산을 최소화하는 Bakshi et al. (1997)이 도입한 근사치를 따릅니다. Lee(2001)는 MV 헤지 비율의 이 조정이 (SM) Smile Implied Delta와 동일한 크기이지만 부호가 반대임을 보여줍니다. 즉,

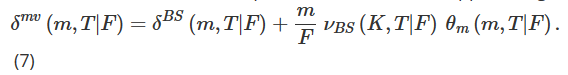
Alexander(2008)의 4장과 묵시적 변동성에 대한 다른 텍스트에서 자세히 설명한 것처럼 미소 묵시적 델타는 반직관적인 “플로팅 스마일” 역학을 생성합니다. 이는 변동성이 클 때를 의미합니다. 그리고 부정적(즉, 상당한 부정적 왜도가 있음)인 경우, SM 조정으로 생성된 헤지 성과는 BS 델타보다 상당히 나쁩니다. MV 조정은 SM 조정과 부호가 반대이므로, 주식 지수 옵션과 상당한 음의 기울기를 갖는 내재 변동성 곡선을 갖는 옵션을 헤지할 때 BS 델타보다 MV 델타를 선호해야 합니다.

우리의 최종 미소 곡선 조정 델타는 δhw로 표시되며 Hull과 White(2017)에 의해 제안되었습니다. BS 델타 헤지 포트폴리오의 일일 PnL ΔP의 절대값과 BS 델타 사이의 이차 관계를 경험적으로 추정하여 도출됩니다. 즉:

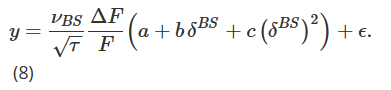
여기서 ΔF는 선물의 일일 PnL입니다. 과거 데이터를 사용하여 매개변수 추정치(aˆ, bˆ, cˆ)를 얻은 후 Hull and White(HW) Delta는 다음과 같이 계산됩니다.

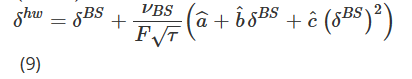
여기서 δBS와 νBS는 고전적 BS 델타와 베가를 나타냅니다. 현재 기초 가격은 F로 표시되고, 그 변화는 ΔF로 표시되며, τ는 옵션의 만기 시간을 나타냅니다. 저자는 36개월 롤링 윈도우를 사용하여 추정치(aˆ, bˆ, cˆ)를 계산한 다음 2014년 1월부터 시작하여 11년 기간 동안 일일 헤지 오류의 표준 편차를 최소화하기 위해 HW 델타 헤지의 성과를 분석합니다. S&P 500 및 기타 주가 지수 옵션. 연구원들은 HW Delta를 사용하면 성능을 최대 26%까지 향상시킬 수 있다는 것을 발견했습니다. 다른 결론은 주가 지수 옵션에만 기초하고 있으며, HW Delta는 콜 옵션의 경우 풋 옵션보다 성과가 좋고, 외가격 옵션의 경우 내가격 옵션보다 성과가 좋다고 주장합니다. 더욱이 그들은 HW Delta가 주식 지수 옵션을 헤지할 때 다양한 확률적 변동성 및 지역적 변동성 모델에서 파생된 많은 다른 델타보다 성과가 우수하다고 주장합니다.

이 섹션에서는 이전의 주식 지수 옵션 헤지와 기타 기존 자산 클래스에 관한 연구에서 효과가 입증된 BS Delta에 대한 일련의 간단한 조정 사항을 다룹니다. 이제 문제는 이들이 비트코인 ​​옵션 시장에서 간단한 BS 델타 헤징보다 더 좋은 성과를 낼 수 있을지 여부입니다. 비트코인 옵션 시장은 전통적인 옵션 시장보다 덜 성숙했으며, 변동성과 매수 압력이 더욱 크며, 시장 조성자들은 이런 압력에서 얻은 정보를 토대로 재고를 재조정합니다. 이 연구에서 고려한 BS 조정 델타 헤지 비율을 다음과 같은 단일 공식으로 요약합니다.

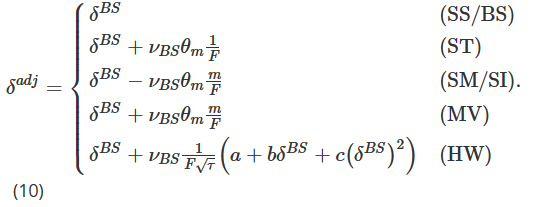
위 내용을 설명하면 다음과 같습니다.

1. m=1인 ​​경우, 즉 등가격 옵션인 경우 MV 조정은 ST 조정과 동일합니다. 그렇지 않은 경우, m>1인 경우, 즉 외가격 콜 옵션인 경우 MV 조정 크기는 ST 조정 크기보다 큽니다. m인 경우, 즉, 외가격 풋 옵션에서 MV 조정 크기는 ST 조정 크기보다 작습니다.

2. MV 조정은 항상 크기가 같고 SM 조정과 방향이 반대이며 SM 델타는 Alexander 및 Nogueira(2007a)의 모델 없는 스케일링 불변(SI) 델타, 즉 모든 유형의 델타입니다. 비트코인 옵션 가격의 확률적 변동성 점프 과정

3. ST, SM, MV 조정의 부호는 암묵적 변동성 곡선의 기울기 θm에 따라 달라집니다. 음의 기울기를 갖는 경우, MV와 ST 델타는 BS/SS 델타보다 작고, SM/SI 델타는 BS/SS 델타보다 큽니다. 양의 기울기를 가질 때, MV와 ST 델타는 BS/SS 델타보다 크고, SM/SI 델타는 BS/SS 델타보다 작습니다.

5. 데이터

우리는 거래소 API를 사용하여 수년에 걸쳐 Deribit 옵션 시장 데이터의 매시간 스냅샷을 촬영하여 고유한 데이터베이스를 만들었습니다. 이 데이터에는 모든 옵션, 선물 및 영구 계약에 대한 레벨 1 주문장 정보가 포함되어 있습니다. 이 기사에서는 2020년 1월 1일부터 2022년 1월 1일까지 2년 동안의 8시간 단위, 일일 빈도의 데이터만 사용했습니다.

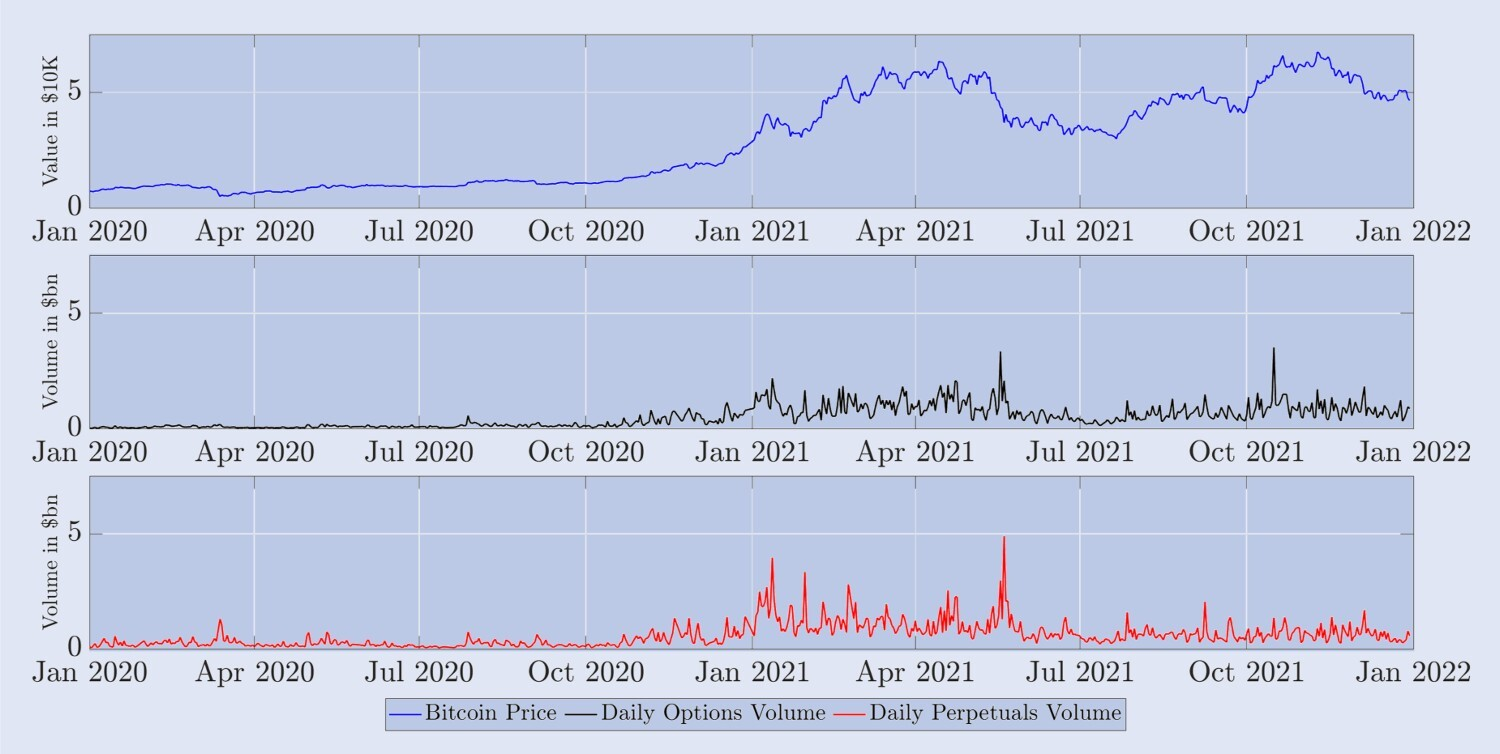
그림 5는 BTC 지수의 일일 결제 가격(즉, 00:00 UTC 기준 가격)과 지난 24시간 동안 Deribit에서 거래된 모든 옵션과 무기한 계약의 총 거래량(명목 금액, 단위: 10억 달러)을 나타냅니다. . 선물 계약은 여기에 포함되지 않습니다. 그림 1에서 볼 수 있듯이 거래량이 영구 계약과 옵션보다 훨씬 낮기 때문입니다. 2020년 동안 BTC 지수는 7,000달러 수준에서 2020년 11월에 시작된 첫 번째 주요 강세장까지 비교적 느리게 상승했으며, 2020년 말까지 지수 가치는 거의 28,000달러에 도달했습니다. 2021년 BTC 지수는 1월(약 28,000달러)부터 4월 중순(약 59,000달러)까지 두 배로 증가한 후, 약 50% 하락하여 7월 중순에 30,000달러로 다시 떨어졌습니다. 2021년 11월 8일에 약 69,000달러로 역대 최고가를 기록했습니다. 그림 5의 가운데 패널은 2020년에 Deribit의 모든 옵션에 대한 24시간 총 거래량이 비교적 낮아서 5억 달러를 간신히 넘었음을 보여줍니다. 그러나 2021년에는 일일 옵션 거래량이 일반적으로 30억 달러에 달하면서 명백히 변동성이 크거나 추세를 보이는 시장이 있었습니다. 거래된 다양한 옵션 계약 수도 2021년 1월 430만 건에서 연말 620만 건으로 거의 두 배나 늘어났습니다. 아래 차트는 2021년에 거래 활동이 활발했던 영구 계약의 일일 거래량을 보여주며, 특히 상반기에 거래 활동이 활발했습니다. 흥미로운 점은 2021년 하반기에 무기한 계약의 거래 증가율이 옵션보다 약했다는 점입니다. 후자는 2020년 후반과 2021년 초에 여러 개의 새로운 계약이 도입되어 거래자들이 감마와 베가 헤지거래에 점차 도입했기 때문일 가능성이 높습니다. 이로 인해 2021년 하반기에 매우 활발했던 동적 델타 헤지에 대한 압박이 완화되었을 수 있습니다. 실제로 그림 1에서 보듯이 선물 계약의 거래량도 2021년 하반기에 영구 계약보다 더 크게 감소했습니다. 그럼에도 불구하고, 2020년과 2021년의 거래 패턴이 너무 다르다는 사실을 발견하여 샘플을 두 개의 1년 기간으로 나누기로 결정했습니다.

그림 5. BTC 지수의 추이와 파생상품의 일일 거래량.

위 차트는 2020년 1월 1일부터 시작하여 2년 샘플 기간 동안 매일 00:00 UTC의 BTC 지수 가격을 보여줍니다(위, 파란색 차트). Deribit의 모든 옵션에 대한 해당 24시간 총 거래량(중앙, 검은색 차트) 차트); 그리고 영구 계약의 일일 거래량(아래, 빨간색 차트). BTC 지수의 가치는 10,000달러 단위이고, 거래량은 수십억 달러입니다.

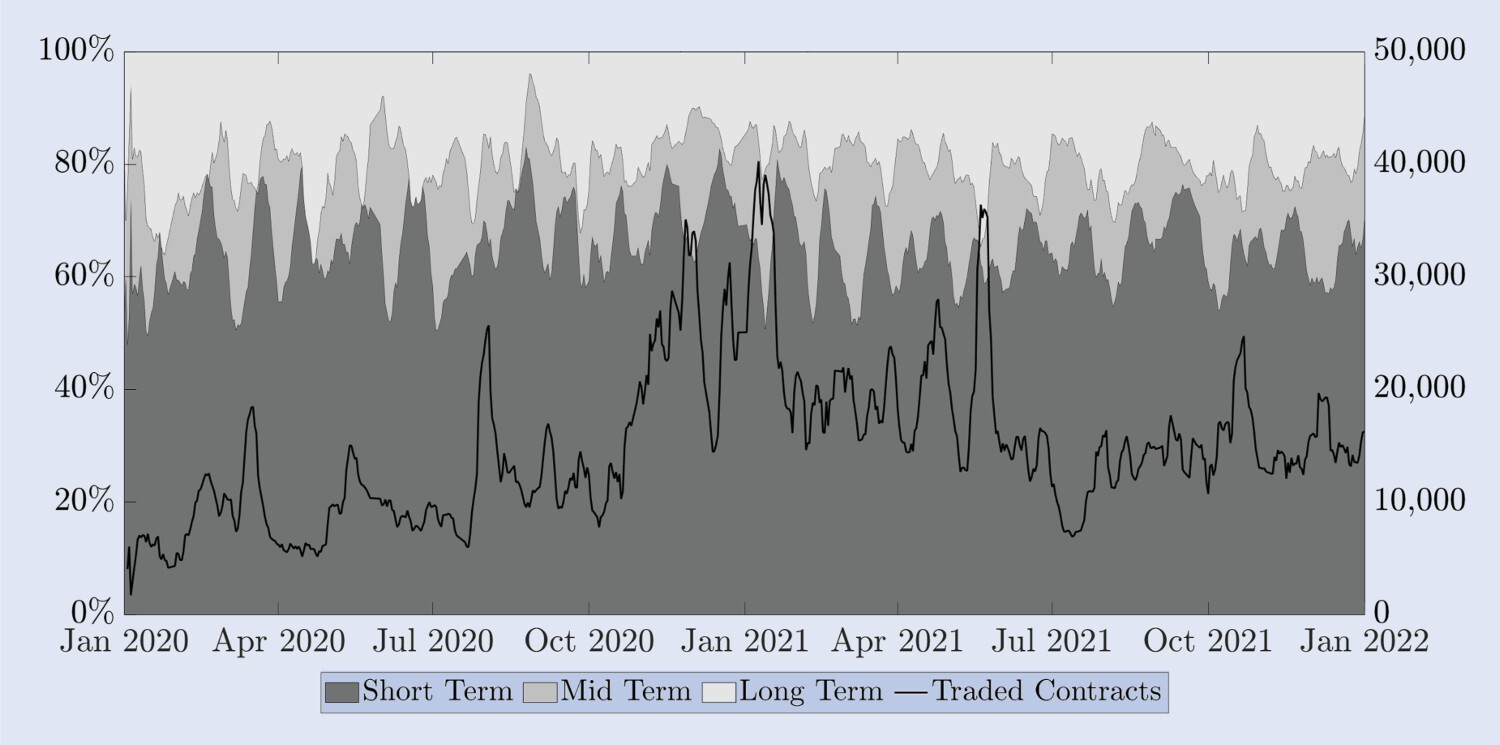
Alexander et al. (2022b)은 비트코인과 S&P 500 옵션 시장 사이에 많은 차이점이 있음을 기록했습니다. 가장 큰 차이점 중 하나는 거래되는 단기, 중기, 장기 옵션의 비율입니다. S&P 500의 1개월 옵션은 대부분 거래가 만기일 1~3개월 사이에 이루어지기 때문에 상대적으로 단기적입니다. 그러나 만기일이 한 달인 비트코인 ​​옵션은 장기 범주에 속합니다. 이를 이해하기 쉽게 설명하자면, 그림 6은 Deribit에서 만료 시간에 따라 거래된 계약 비율을 나타냅니다. 오른쪽 눈금의 실선은 만료되는 모든 계약에 대한 거래 수를 나타냅니다. 명확성을 위해, 우리는 일정 기간 동안의 주별 평균을 사용하여 이 데이터를 제시합니다. 단기 옵션(최대 2주) 비율의 계절적 패턴은 발행 일정 정책의 결과입니다. 즉, 해당 주(또는 2주)에 만료되는 표준 월별 또는 분기별 옵션이 없는 한 옵션은 현재 주(또는 2주)까지 발행됩니다. 1주일(및/또는 2주) 만료일이 있는 옵션. 왼쪽 눈금에는 단기(최대 2주), 중기(2주에서 1개월), 장기(1개월 이상) 만기의 비중을 나타냅니다. 이를 위해 각 만기 범주 내에서 당일 거래된 모든 계약을 집계하여 모든 거래된 계약의 백분율로 표시하며, 명확성을 위해 이번에도 이동 기간 주간 평균을 사용합니다. 이러한 계절적 패턴을 제외하면 2년 전체 기간 동안 만기일이 1개월 이상인 옵션 거래는 전체의 15~20%에 불과했습니다. 샘플에서 거래되는 계약 수가 증가하고 있음에도 불구하고 만기가 1개월 이상인 계약의 비율은 비교적 안정적으로 유지되었으며, 2주 이내에 만기가 되는 단기 옵션의 비율도 마찬가지였습니다. 실제로 거래되는 모든 계약의 약 60%가 이처럼 매우 단기적인 만료 기간에 해당합니다. 거래된 계약의 20%~25%는 만료 기간이 2주에서 1개월 사이인 ‘중기’ 옵션에 해당합니다. Deribit의 전체 거래량에서 만기가 한 달인 옵션이 80~85%를 차지하기 때문에 우리는 이 옵션에 대한 헤지 리서치를 집중하기로 결정했습니다. 만기가 1개월 이상인 옵션은 시간당 빈도로 분석하더라도 경험적 분석에 유용할 만큼 오래된 가격이 너무 많습니다. 이는 위에서 설명한 각 만료 범주에서 하나의 옵션을 고려해 보도록 촉구합니다. 비교의 편의성을 위해 우리는 10일, 20일, 30일 만기 옵션을 연구 대상으로 선택했습니다. 각각은 세 가지 주요 만기 범주를 대신합니다.

그림 6. 거래된 옵션의 만기일.

왼쪽의 스케일은 단기 옵션(2주 이내, 진한 회색), 중기 옵션(2주에서 1개월 사이, 중간 회색), 장기 옵션(1개월 이상)의 비율을 보여줍니다. 총 거래량에서 (연한 회색)이 감소했습니다. 검은색 선(오른쪽 눈금)은 거래된 옵션 계약의 총 수를 나타냅니다. 모든 시리즈는 일일 데이터의 주별 이동 평균입니다.

다음으로 데이터 필터링�