저는 최근 제한 주문장을 조사한 여러 논문에서 얻은 주요 통찰력을 요약했습니다. 주문장에서 거래량 불균형을 측정하는 방법과 가격 움직임에 대한 예측 능력에 대해 알아봅니다. 이 글에서는 주문장 데이터를 사용하여 가격 움직임을 모델링하는 방법을 살펴봅니다.

먼저 주문서에 대해 이야기해 보겠습니다.

거래소 주문장 잔액은 거래소 내 매수 주문과 매도 주문의 상대적 잔액을 말합니다. 주문장은 시장에서 보류 중인 모든 매수 및 매도 주문을 실시간으로 기록한 것입니다. 여기에는 서로 다른 가격으로 거래할 의향이 있는 구매자와 판매자의 주문이 포함됩니다.

거래소 주문서 잔액과 관련된 몇 가지 주요 개념은 다음과 같습니다.

• 매수자 및 매도자 주문: 주문장의 매수자 주문은 특정 가격으로 자산을 매수하려는 투자자를 나타내고, 매도 주문은 특정 가격으로 자산을 매도하려는 투자자를 나타냅니다.

• 주문장 깊이: 주문장 깊이는 매수 및 매도 측의 주문 수를 말합니다. 깊이가 깊다는 것은 시장에 매수 및 매도 주문이 더 많다는 것을 의미하며 유동성이 더 높을 수 있습니다.

• 거래 가격 및 거래량: 거래 가격은 가장 최근의 거래 가격이고, 거래량은 해당 가격으로 거래된 자산의 수입니다. 거래 가격과 거래량은 주문장상의 매수자와 매도자 간의 경쟁에 따라 결정됩니다.

• 주문장 불균형: 주문장 불균형은 매수 주문 수와 매도 주문 수 또는 총 거래량의 차이를 말합니다. 이는 주문장의 깊이를 살펴보면 알 수 있습니다. 한 쪽이 다른 쪽보다 훨씬 많은 주문을 가지고 있다면 주문장 불균형이 있을 수 있습니다.

• 시장 심도 차트: 시장 심도 차트는 주문장의 심도와 잔액을 그래픽으로 표현합니다. 일반적으로 구매자와 판매자의 주문 수는 가격 수준에 따라 막대형 차트나 다른 시각적 형식으로 표시됩니다.

• 가격에 영향을 미치는 요소: 주문장 잔액은 시장 가격에 직접적인 영향을 미칩니다. 구매자의 주문이 많아지면 가격이 올라갈 수 있고, 반대로 판매자의 주문이 많아지면 가격이 떨어질 수 있습니다.

• 고빈도 거래 및 알고리즘 거래: 고빈도 거래 및 알고리즘 거래에서는 주문장 밸런싱이 매우 중요합니다. 이는 시장 기회를 빠르게 포착하기 위한 의사 결정을 내리기 위해 실시간 주문장 데이터에 의존하기 때문입니다.

주문장 잔액을 이해하는 것은 투자자, 트레이더, 시장 분석가에게 중요합니다. 이는 시장 유동성, 잠재적 가격 방향, 시장 동향에 대한 유용한 정보를 제공하기 때문입니다.

불균형한 볼륨

지정가 주문장을 분석할 때 가장 중요한 아이디어는 시장 전체가 매수에 더 관심이 있는지, 매도에 더 관심이 있는지 판단하는 것입니다. 이 개념을 볼륨 불균형이라고 합니다.

시간 t에서의 부피 불균형은 다음과 같이 정의됩니다.

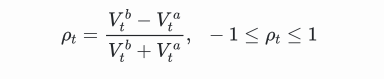
이 중 \(V_{t}^{b}\)는 시점 t에서의 최상 매수 주문의 거래량이고, \(V_{t}^{a}\)는 시점 t에서의 최상 매도 주문의 거래량이다. \(ρ_{t}\)가 1에 가까울수록 강한 매수 압력으로 해석할 수 있고, \(ρ_{t}\)가 -1에 가까울수록 강한 매도 압력으로 해석할 수 있습니다. 여기에는 최고 매수 및 최고 매도 주문량, 즉 L1 주문장부만 고려됩니다.

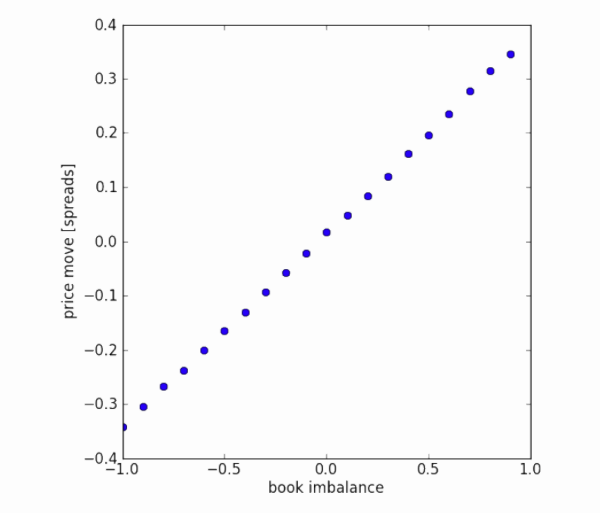
거래량 불균형과 가격 변동. 그래프는 트랜치의 거래량 불균형(x축)과 스프레드로 정규화된 미래 가격 변동의 평균(y축)을 보여줍니다. 데이터 집합은 한 분기 동안의 시장 주문 흐름입니다. 1차 주문장의 불균형과 향후 가격 변동 사이에는 선형 관계가 있는 것으로 보입니다. 그러나 평균적으로 미래 가격 움직임은 매수-매도 가격 차이 내에 있습니다.

체적 불균형 \(ρ_{t}\)는 다음의 세 가지 섹션으로 나뉩니다.

다음 세그먼트는 향후 가격 변동을 예측할 수 있는 것으로 나타났습니다.

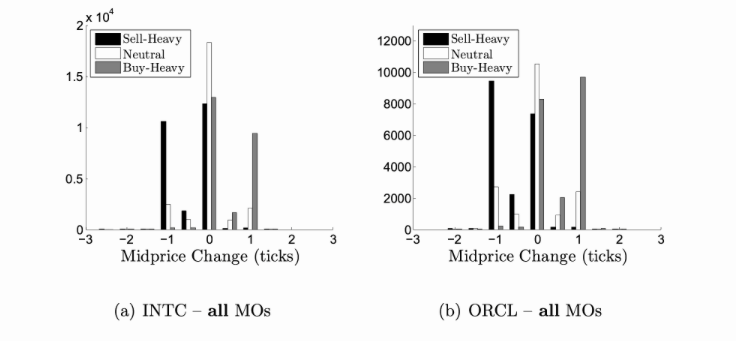
거래량 불균형의 예측 능력과 관련하여, 2014년 1월부터 12월까지 특정 심볼의 틱별 주문장을 분석했습니다. 도착하는 각 시장 주문(MO)에 대해 거래량 불균형이 기록되고 다음 10밀리초 내의 중간 가격 변화의 틱 수에 따라 세분화됩니다. 차트는 각 세그먼트의 분포와 중간값 가격 변화를 보여줍니다. 매수 압력이 더 커지면서 주문장에 앞서 긍정적인 가격 변동이 발생할 가능성이 더 높다는 것을 알 수 있습니다. 마찬가지로, 강한 매도 압력이 가해지는 주문장에 앞서 부정적인 움직임이 발생할 가능성이 더 큽니다.

주문 흐름 불균형

거래량 불균형은 지정가 주문장의 전체 거래량을 살펴봅니다. 한 가지 단점은 이 책의 일부가 오래된 주문에서 나온 것이어서 관련성이 낮은 정보를 담고 있다는 것입니다. 대신 우리는 최근 주문량에 집중할 수 있습니다. 이 개념을 주문 흐름 불균형이라고 합니다. 개별 시장 및 지정가 주문을 추적하거나(레벨 3 데이터 필요) 지정가 주문장의 변경 사항을 살펴보면 이를 확인할 수 있습니다.

레벨 3 데이터는 비용이 많이 들고 일반적으로 기관 거래자에게만 제공되므로, 여기서는 지정가 주문장의 변화에 ​​초점을 맞출 것입니다.

우리는 최적 매수 가격 및 최적 매도 가격에서 얼마나 많은 거래량이 이동했는지 알아내어 주문 흐름 불균형을 계산할 수 있습니다. 최고 입찰 가격에서의 거래량 변화는 다음과 같습니다.

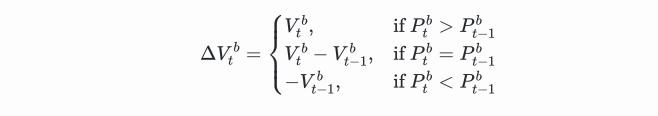
이는 세 가지 사례를 포함하는 함수입니다. 첫 번째 경우는 최고 입찰가가 이전 최고 입찰가보다 높으면 모든 거래량이 새로운 거래량입니다.

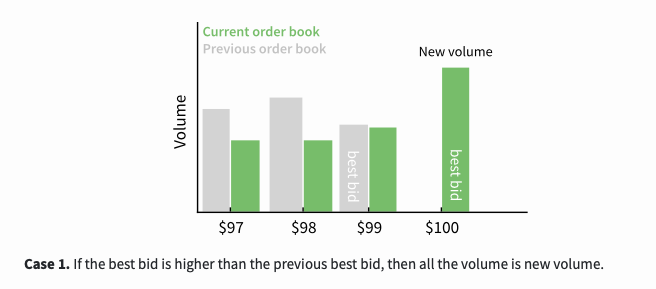
두 번째 경우는 최고 입찰가가 이전 최고 입찰가와 동일한 경우, 새로운 거래량은 현재 총 거래량과 이전 총 거래량의 차이입니다.

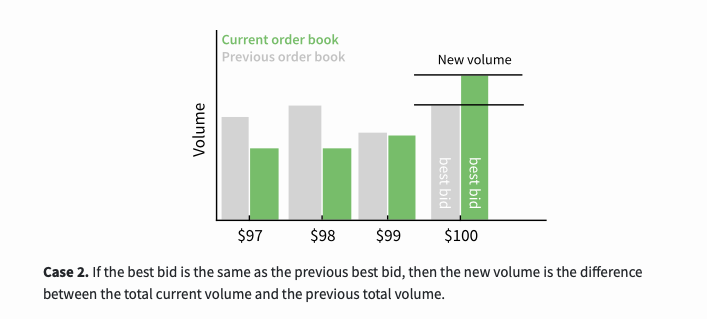
세 번째 경우는 최고 입찰 가격이 이전 최고 입찰 가격보다 낮은 경우, 이전에 보류 중인 모든 주문은 이행되어 더 이상 주문장에 존재하지 않게 됩니다.

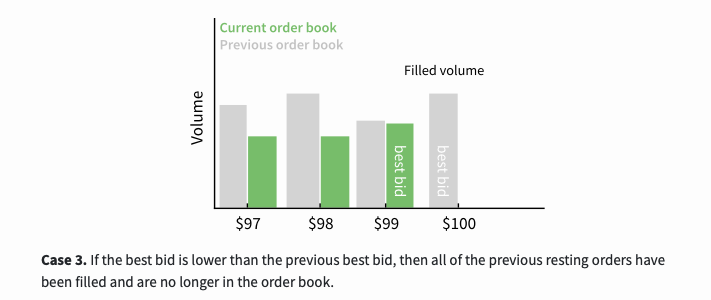
최상의 매도 가격에서의 볼륨 변화에 대한 계산은 유사합니다.

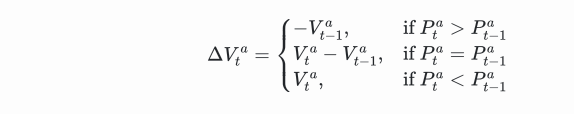
시간 t에서의 순 주문 흐름 불균형(OFI)은 다음 공식으로 주어집니다.

\(OFI_{t} = \Delta V_{t}^{b,1} - \Delta V_{t}^{a,1}\)

매수 주문이 많으면 긍정적이고, 매도 주문이 많으면 부정적입니다. 이는 부피의 양과 방향을 모두 측정합니다. 이전 섹션에서 볼륨 불균형은 볼륨의 양이 아닌 방향만 측정했습니다.

이러한 값을 함께 추가하면 시간 경과에 따른 순 주문 흐름 불균형(OFI)을 얻을 수 있습니다.

\(\sum_{i=t-n}^{t} OFI_i\)

회귀 모델을 사용하여 주문 흐름 불균형에 미래 가격 변동에 대한 정보가 포함되어 있는지 테스트합니다.

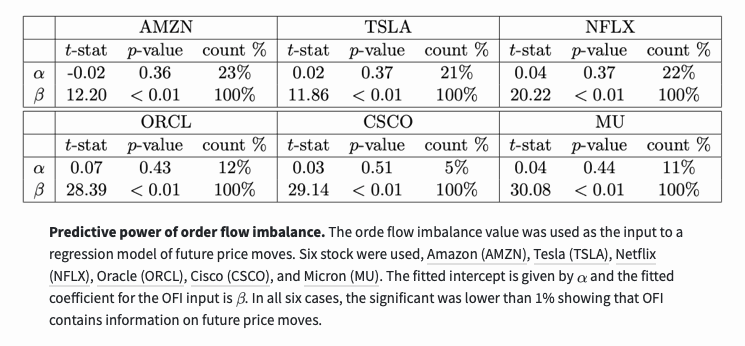
위에서 계산된 OFI 가치는 최고 매수 가격과 최고 매도 가격에 초점을 맞춥니다. 4번째 부분에서는 상위 5개의 최적 가격의 값도 계산되며, 1개가 아닌 5개의 입력값이 제공됩니다. 그들은 주문장을 더욱 깊이 파고들면 미래의 가격 움직임에 대한 새로운 정보를 얻을 수 있다는 것을 발견했습니다.

요약하다

여기서는 지정가 주문장에서 주문량을 연구한 몇몇 논문에서 얻은 주요 통찰력을 요약해보겠습니다. 이들 논문은 주문장에 미래의 가격 움직임을 매우 예측할 수 있는 정보가 담겨 있음을 보여줍니다. 하지만 이러한 움직임은 입찰-매도 가격 차이를 극복할 수 없습니다.

참고문헌 섹션에 해당 논문의 링크를 추가했습니다. 자세한 내용은 검토하세요.

References & Notes

• Álvaro Cartea, Ryan Francis Donnelly, and Sebastian Jaimungal: “Enhancing Trading Strategies with Order Book Signals” Applied Mathematical Finance 25(1) pp. 1–35 (2018)
• Alexander Lipton, Umberto Pesavento, and Michael G Sotiropoulos: “Trade arrival dynamics and quote imbalance in a limit order book” arXiv (2013)
• Álvaro Cartea, Sebastian Jaimungal, and J. Penalva: “Algorithmic and high-frequency trading.” Cambridge University Press
• Ke Xu, Martin D. Gould, and Sam D. Howison: “Multi-Level Order-Flow Imbalance in a Limit Order Book” arXiv (2019)

출처: 저자 ~ {리치포드, 에이드리언}.