베이지안 통계학은 금융, 의학 연구, 정보 기술을 포함한 여러 분야에 폭넓게 응용되는 수학의 강력한 학문입니다. 이를 통해 우리는 사전 신념과 증거를 결합하여 새로운 사후 신념에 도달할 수 있고, 이를 통해 더욱 정보에 입각한 결정을 내릴 수 있습니다.

이 글에서는 이 분야를 창시한 주요 수학자 몇 명을 간략히 소개하겠습니다.

베이즈 이전 베이지안 통계학을 더 잘 이해하려면 18세기로 돌아가 수학자 드 무아브르(De Moivre)와 그의 논문 “우연의 원리(The Principle of Chance)“를 참조해야 합니다.[1]。

드 무아브르는 그의 논문에서 확률과 도박에 관련된 당시의 많은 문제를 다루었습니다. 아마 여러분도 알고 계시겠지만, 이 문제 중 하나에 대한 그의 해결책이 정규분포의 기원을 낳았습니다. 하지만 그것은 또 다른 이야기입니다.

그의 논문에는 간단한 질문이 있습니다.

“공정한 동전을 세 번 연속으로 던졌을 때 세 번 모두 앞면이 나올 확률.”

“우연의 원리”에 설명된 문제들을 읽어보면, 대부분의 문제가 주어진 사건의 확률을 계산하는 가설에서 시작한다는 것을 알 수 있습니다. 예를 들어, 위의 문제에서는 동전이 공평하다는 가정이 있습니다. 즉, 동전을 던져서 앞면이 나올 확률은 0.5입니다.

이는 오늘날 수학적으로 다음과 같이 표현됩니다.

𝑃(𝑋|𝜃)

하지만 동전이 공정한지 알 수 없다면 어떨까요? 우리가 모른다면𝜃모직물?

토마스 베이즈와 리차드 프라이스

거의 50년 후인 1763년에 “우연의 원리에 관한 에세이”라는 제목의 논문이 발표되었습니다.[2] 런던 왕립학회 철학회보에 게재됨.

이 문서의 처음 몇 페이지에는 수학자 리처드 프라이스가 쓴 글이 있는데, 그의 친구 토마스 베이즈가 죽기 몇 년 전에 쓴 논문의 내용을 요약한 것입니다. 서론에서 프라이스는 드 무아브르의 우연의 원리에서 다루지 않은 토마스 베이즈의 몇 가지 발견의 중요성을 설명합니다.

사실 그는 구체적인 문제를 언급하고 있었습니다.

“알려지지 않은 사건의 발생 횟수와 실패 횟수를 고려하여, 두 개의 명명된 확률도 사이에 발생할 가능성을 찾으십시오.”

즉, 사건을 관찰한 후에 우리는 알려지지 않은 매개변수를 찾습니다.θ두 확률 사이의 확률은 무엇입니까? 이는 실제로 통계적 추론과 관련된 역사상 최초의 문제 중 하나이며, 역확률이라는 이름이 생겨났습니다. 수학적으로 표현하면:

𝑃( 𝜃 | 𝑋）

물론 이는 오늘날 우리가 베이즈 정리의 사후 분포라고 부르는 것입니다.

원인 없는 원인

이 두 명의 원로 목사님을 알아보세요.토마스 베이즈그리고리차드 프라이스사실, 연구의 동기는 매우 흥미롭습니다. 하지만 이를 위해서는 잠시 통계에 대한 지식을 숙지해야 합니다.

우리는 18세기에 살고 있으며, 확률은 수학자들에게 점점 더 큰 관심을 끄는 분야가 되고 있습니다. 드 무아브르나 베르누이와 같은 수학자들은 일부 사건이 어느 정도 무작위적으로 발생하지만 여전히 고정된 규칙에 따라 지배받는다는 것을 보였습니다. 예를 들어, 주사위를 여러 번 굴리면 6번 중 1번은 6이 나올 것입니다. 마치 우연의 운명을 결정하는 숨겨진 규칙이 있는 것 같습니다.

이제 당신이 이 시대에 사는 수학자이자 독실한 신자라고 상상해보세요. 당신은 이 숨겨진 규칙이 신과 어떤 관련이 있는지 궁금할지도 모릅니다.

이것은 실제로 베이즈와 프라이스가 직접 물은 질문이었습니다. 그들이 이 문제를 해결하기 위해 바랐던 해결책은 “세상은 지혜와 지성의 결과여야 한다”는 것을 증명하는 데 직접적으로 적용될 수 있었습니다. 따라서 궁극적 원인으로서의 신의 존재에 대한 증거를 제공했습니다.[2] - 즉, 인과관계가 없습니다.

라플라스

놀랍게도 그로부터 약 2년 후인 1774년에 프랑스 수학자 라플라스는 토마스 베이즈의 논문을 읽지 않은 듯 “사건의 확률을 통한 사건의 원인에 관하여”라는 제목의 논문을 썼습니다.[3]은 역확률 문제에 관한 논문입니다. 첫 번째 페이지에서 다음을 읽을 수 있습니다.

주요 원칙은 다음과 같습니다.

“사건이 n개의 서로 다른 원인에 의해 발생할 수 있다면, 주어진 사건에 대한 이들 원인의 확률은 원인을 기준으로 한 사건의 확률과 동일한 비율로 존재하며, 이들 각각의 원인의 존재 확률은 다음과 같습니다. 원인을 감안한 사건의 확률. 원인의 확률을 각 원인을 감안한 사건의 확률의 합으로 나눈 값입니다.”

이것이 오늘날 우리가 베이즈 정리로 알고 있는 것입니다.

​

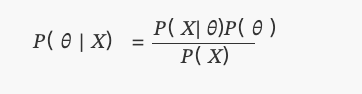
~에P(θ)균일하게 분포되어 있습니다.

동전 실험

Python과 PyMC 라이브러리를 사용하여 베이지안 통계를 현재에 적용하고 간단한 실험을 수행해 보겠습니다.

친구가 당신에게 동전을 주고 그것이 공평한 동전이라고 생각하느냐고 물었다고 가정해 보자. 그는 서두르기 때문에 동전을 10번만 던지라고 말합니다. 보시다시피 이 문제에는 알 수 없는 매개변수가 있습니다.p동전 던지기에서 앞면이 나올 확률을 추정하고 싶습니다.p가장 가능성 있는 값은 .

(참고: 우리는 매개변수에 대해 이야기하는 것이 아닙니다.p는 확률 변수이지만, 이 매개변수는 고정되어 있으며 우리는 어느 값 사이에 있을 가능성이 가장 큰지 알고 싶습니다. ）

이 문제에 대해 다른 관점을 얻기 위해 우리는 두 가지 다른 사전 신념에 따라 이 문제를 다루어보겠습니다.

• 1. 당신은 동전의 공정성에 대한 사전 정보가 없으며 동일한 확률을 할당합니다.p. 이 경우, 우리는 소위 ‘비정보적 사전 지식’을 사용할 것입니다. 왜냐하면 당신은 당신의 믿음에 아무런 정보도 추가하지 않기 때문입니다.
• 1. 당신은 동전이 불공평하더라도 그것을 매우 불공평하게 만드는 것이 어렵다는 것을 경험으로 알고 있으므로 매개변수를 생각합니다.p아마도 0.3 이하로 내려가거나 0.7 이상 올라가지는 않을 것입니다. 이 경우에는 정보적 사전 지식을 활용하겠습니다.

두 경우 모두 우리의 사전 믿음은 다음과 같습니다.

동전을 10번 던지면 앞면이 두 번 나옵니다. 이 증거를 통해 우리는 아마도 매개변수를 찾을 수 있는 곳을 알아낼 수 있을 것입니다.p？

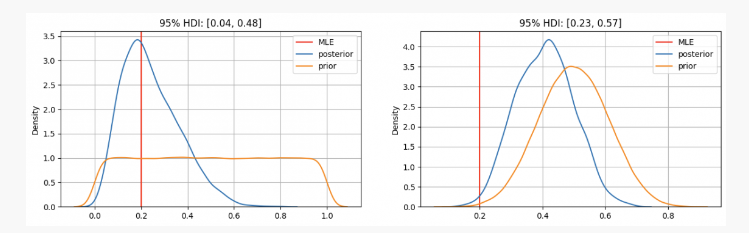
보시다시피, 첫 번째 경우에는 다음과 같습니다.p사전 분포는 최대 우도 추정치(MLE)를 중심으로 합니다.p=0.2이는 빈도주의적 방법을 사용하는 유사한 접근 방식입니다. 실제로 알려지지 않은 매개변수는 95% 신뢰 구간인 0.04와 0.48 사이에 위치하게 됩니다.

반면, 매개변수에 대한 신뢰도가 높은 경우p 사후 분포는 0.3과 0.7 사이여야 하지만, MLE가 제시한 값보다 훨씬 높은 0.4 정도에 있음을 알 수 있습니다. 이 경우, 실제로 알려지지 않은 매개변수는 95% 신뢰 구간인 0.23과 0.57 사이에 위치하게 됩니다.

그래서 첫 번째 경우라면, 당신은 친구에게 그 동전이 불공평하다는 것을 확신한다고 말할 것입니다. 하지만 다른 경우에는 동전이 공정한지 잘 모르겠다고 말할 것입니다.

보시다시피, 같은 증거가 있더라도(10번 던지면 2번 앞이 나옴) 사전 믿음이 다르면 결과가 달라질 수 있습니다. 이는 베이지안 통계의 장점으로, 과학적 방법과 유사하게 사전 신념에 새로운 관찰 및 증거를 결합하여 신념을 업데이트할 수 있게 해줍니다.

END

오늘의 기사에서는 베이지안 통계의 기원과 주요 기여자에 대해 알아보았습니다. 그 이후로 통계학이라는 분야에 많은 중요한 기여를 한 사람들이 생겨났으며(제프리스, 콕스, 섀넌 등), 이들은 quantdare.com에서 인용한 바 있습니다.