이중 간격 필터링 동적 추세 추적 전략

개요

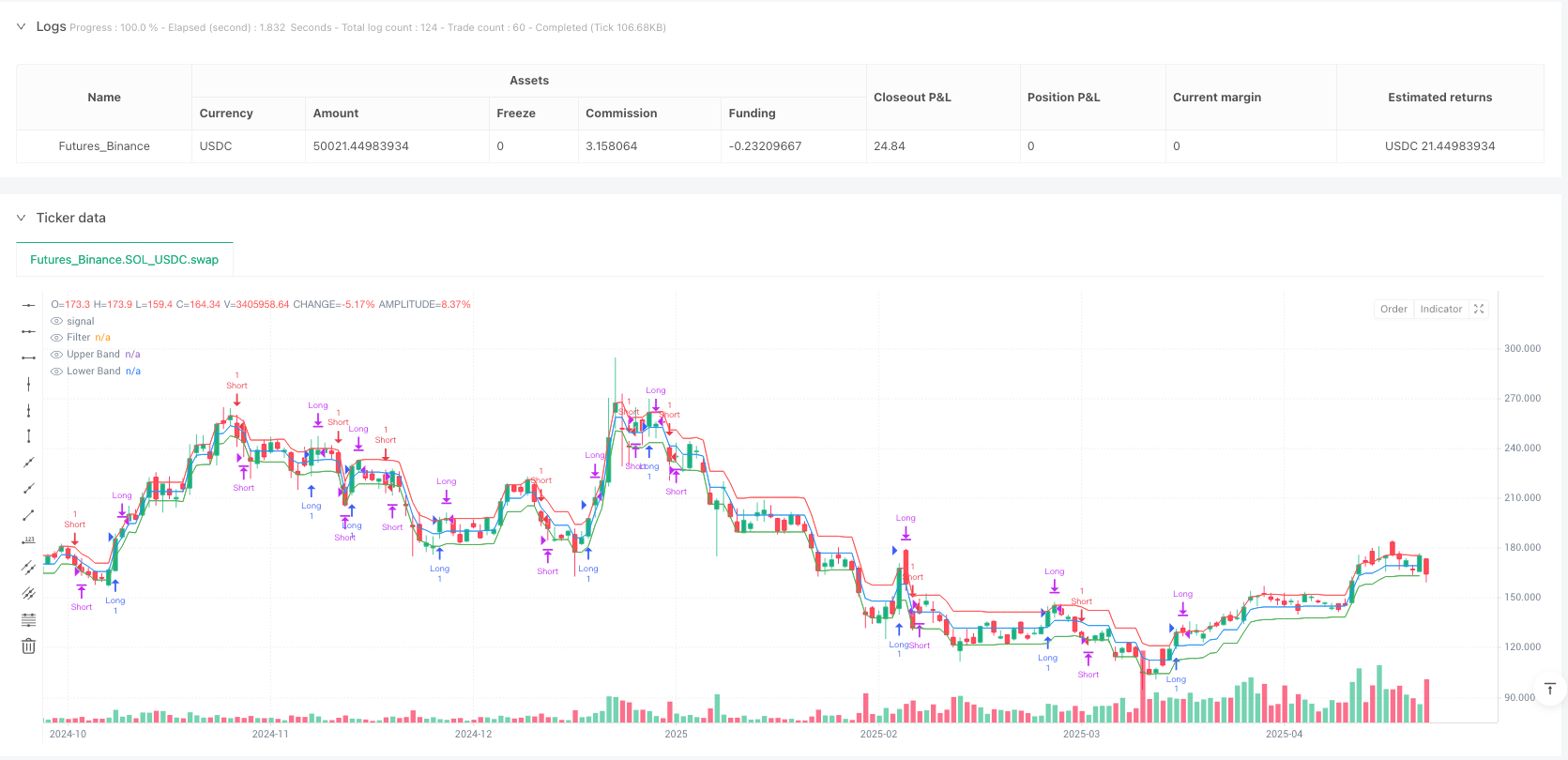
이중 간격 파동 동향 추적 전략은 가격 변동성에 기반한 지능형 거래 시스템으로, 빠르고 느린 두 개의 독립된 필터를 결합하여, 이중 확인된 트렌드 식별 메커니즘을 구축한다. 이 전략의 핵심은 지수 이동 평균 ((EMA) 를 사용하여 평평한 평균 실제 파장을 계산하는 것이며, 그 다음이 동적 변동성 지표에 기반하여 상하 궤도를 구축하여, 자율적인 가격 통로를 형성한다. 가격이 이 동적 동향 통로를 뚫을 때, 이 전략은 뚫는 방향과 트렌드 지속성에 따라 상응하는 거래 신호를 생성한다.

이 전략은 특히 렌코 차트에 적합하며, 렌코 차트는 시간적 요소를 필터링하여 가격 변화에 집중할 수 있기 때문에, 이 전략은 간격 波 전략의 핵심 사상과 매우 일치합니다. 이 전략은 이중 간격 波 메커니즘을 통해 거래 의사 결정에 대한 시장 소음의 간섭을 효과적으로 줄이고, 실제 트렌드 변화에 대한 민감성을 유지합니다. 이 디자인은 전략이 흔들리는 시장에서 빈번한 가짜 신호를 피할 수 있도록하고, 트렌드 시장에서 효과적인 가격 돌파구를 적시에 잡을 수 있습니다.

전략의 지능화는 다양한 시장 변동 환경에 적응하기 위해 범위를 동적으로 조정하여 높은 변동성 시장에서 너무 민감하지 않고 낮은 변동성 시장에서 너무 느려지지 않도록하는 것으로 나타납니다.

전략 원칙

이중 간격 동 동향 트렌드 추적 전략의 핵심 원칙은 가격 변동성의 통계적 특성에 기초한다. 전략은 먼저 smoothrng 함수를 통해 평평한 평균 변동 범위를 계산하고, 이 함수는 지수 이동 평균을 사용하여 가격의 절대 변화 값을 두 번 평평 처리한다. 첫 번째 평평은 가격 변화의 절대 값을 계산하는 EMA이며, 두 번째 평평은 원주기의 두 배로 감소하는 주기를 사용한다. 이중 평평 메커니즘은 효과적인 단기간의 소음을 제거하면서 중기 및 장기간의 변동성에 대한 대응력을 유지한다.

이 전략은 빠르고 느린 두 가지의 파라미터 시스템을 설계했습니다. 빠른 파라미터 ((per1=27, mult1=1.5) 는 단기 가격 변화를 포착하고 느린 파라미터 ((per2=55, mult2=1.0) 는 장기 트렌드를 식별합니다. 두 세트 사이의 평균은 최종 동적 영역 폭으로 설계되어 전략의 민감성과 안정성을 균형을 맞추고 있습니다.

간격 필터 (rngfilt 함수) 는 전략의 핵심 구성 요소이며, 현재 가격과 이전 기간의 간격 값과의 관계를 비교하여 파동 선의 위치를 동적으로 조정한다. 가격이 상승할 때, 파동 선은 현재 가격으로 하락한 간격 너비와 이전 기간의 간격 값의 더 큰 것으로 설정된다. 가격이 하락할 때, 파동 선은 현재 가격에 추가된 간격 너비와 이전 기간의 간격 값의 더 작은 것으로 설정된다. 이 메커니즘은 파동 선이 가격 추세 변화에 따라 움직일 수 있도록 보장하며, 간격 단기 변동을 통과 할 수있는 충분한 완충권을 제공합니다.

전략은 상향과 하향 변수를 통해 연속적으로 상승과 하락의 기간을 기록합니다. 이 계산 메커니즘은 트렌드의 강도와 지속성을 판단하는 데 도움이 됩니다. 거래 신호의 생성은 가격에 대한 파동선의 위치 관계와 트렌드 방향의 지속성의 두 가지 조건을 충족해야합니다. 이 쌍 확인 메커니즘은 신호의 신뢰성을 크게 향상시킵니다.

전략적 이점

이중 간격 변동 동향 추적 전략에는 여러 가지 중요한 장점이 있습니다. 첫째, 탁월한 자기 적응력으로, 전략은 시장의 변동성에 따라 범위를 자동으로 조정할 수 있습니다. 이것은 높은 변동성이있는 시장에서 전략이 관용 범위를 확장하고 오해를 줄 수 있음을 의미합니다. 낮은 변동성이있는 시장에서 전략은 범위를 강화하고 민감성을 향상시킵니다. 이러한 자기 적응 메커니즘은 다양한 시장 환경에서 전략을 안정적으로 유지할 수 있습니다.

두 번째 장점은 두 개의 확인 메커니즘의 장점이다. 전략은 두 개의 빠른 및 느린 필러브 시스템을 결합하고 가격 위치 및 추세 지속성의 두 개의 검증을 통해 가짜 신호의 가능성을 크게 감소시킵니다. 이 디자인은 특히 금융 시장에서 흔히 발생하는 노이즈 거래 및 단기 변동 장애를 처리하는 데 적합합니다.

전략의 또 다른 중요한 장점은 뛰어난 트렌드 추적 능력이다. 연속적인 계산 메커니즘을 통해 전략은 강력한 트렌드를 식별하고 지속적으로 추적하여 수익성있는 위치를 조기 종료하는 것을 피할 수 있다. 동시에, 트렌드가 역전되면 전략은 또한 위치를 조정하는 방향을 적시에 식별하고 조정할 수 있다.

위험 관리의 관점에서, 전략은 동적 중단 메커니즘을 내장한다. 상하 궤도의 디자인은 자연적으로 위험 제어 기능을 제공하며, 가격이 궤도를 돌파 할 때 거래 신호를 유발하고, 가격이 궤도에 돌아 올 때 중단 또는 평점을 유발할 수 있습니다. 이러한 디자인은 각 거래에 명확한 위험 경계선이 있음을 보장합니다.

전략은 또한 좋은 변수 안정성을 가지고 있다. 여러 가지 조정 가능한 변수가 있지만, 전략은 변수에 대한 민감성이 상대적으로 낮아, 이는 전략이 다양한 시장 환경에서 상대적으로 안정적인 성능을 유지할 수 있다는 것을 의미하며, 과도한 최적화의 위험을 줄인다.

전략적 위험

이중 간격 동 동향 트렌드 추적 전략은 많은 장점이 있지만, 여전히 주의해야 할 몇 가지 위험점이 있습니다. 가장 주요한 위험은 흔들리는 시장에서의 성능 문제입니다. 시장이 수평 평정 상태일 때, 가격은 종종 동선을 통과하여 전략이 과도한 거래 신호를 발생시킬 수 있습니다. 이중 확인 메커니즘은 이러한 상황을 줄일 수 있지만, 강력한 흔들리는 시장에서 전략은 계속되는 작은 손실의 위험에 직면 할 수 있습니다.

해결책은 추가적인 시장 환경 인식 모듈을 추가하는 것을 포함합니다. 예를 들어, 변동성 지표 또는 트렌드 강도 지표가 도입되어 현재 시장이 전략 실행에 적합한지 판단합니다. 강력한 충격적인 환경이 감지되면 거래를 일시 중단하거나 파라미터 설정을 조정할 수 있습니다.

또 다른 중요한 위험은 지연성 문제입니다. 전략이 이중 EMA 완화 및 이중 확인 장치를 사용하기 때문에, 트렌드 전환의 초기에는 전략이 적시에 대응하지 못할 수 있으며, 이로 인해 최적의 입시 시기를 놓치거나 불필요한 철수를 겪을 수 있습니다. 이러한 지연성은 빠르게 변화하는 시장에서 특히 분명합니다.

지연 문제를 완화하기 위해, 선도 지표 또는 가격 행동 분석 모듈을 도입하는 것이 고려 될 수 있습니다. 예를 들어, 가격의 가속 변화 또는 중요한 지지 저항 지점의 돌파구를 모니터링하십시오. 또한, 전략의 안정성을 유지하는 전제 하에 파라미터 조합을 최적화하여 대응 속도를 적절하게 향상시킬 수 있습니다.

변수 민감도는 상대적으로 낮지만, 과잉 최적화의 위험은 여전히 존재한다. 역사적 데이터에 대해 과잉 조정된 변수는 실제 거래에서 전략이 좋지 않은 결과를 초래할 수 있다. 전향 분석과 샘플 외 테스트를 사용하여 변수의 건전성을 검증하는 것이 좋습니다.

또한, 극단적 인 시장 조건에서 전략의 성과에 대한 특별한 관심이 필요합니다. 블랙 스윙 사건이나 유동성 위기가 발생하면 정상적인 가격 행동은 실패하여 전략에 대한 예상치 못한 큰 손실을 초래할 수 있습니다.

전략 최적화 방향

이중 간격 변동 동향 추적 전략에는 추가로 최적화 할 수있는 여러 방향이 있습니다. 첫째, 시장 환경 적응성의 강화입니다. ATR 기반의 변동성 계열이나 VIX 계열의 지표 기반의 시장 감정 분석과 같은 변동성 상태 분류 시스템을 도입 할 수 있습니다.

다음으로 신호 품질을 더 향상시킬 수 있습니다. 물량 가격 연동 분석을 도입하는 것이 고려 될 수 있으며, 가격이 필로파인 라인을 돌파 할 때 거래량과 함께 증폭되면 신호의 신뢰성을 높일 수 있습니다. 또한, 중요한 기술 비트 분석과 결합하여 중요한 지지 저항 지점 근처에서 돌파구가 발생할 때 더 높은 무게를 부여 할 수 있습니다.

동적 변수 조정 (Dynamic parameter adjustment) 은 또 다른 중요한 최적화 방향이다. 현재의 전략은 고정된 주기적 변수를 사용하지만 시장의 주기적 특징은 동적 변화이다. 시장의 변동성 주기 및 트렌드 지속적 동력에 따라 적응 변수 메커니즘을 도입할 수 있다. 예를 들어, 트렌드 시장에서 시끄러운 것을 줄이기 위해 주기적 변수를 연장하고, 흔들리는 시장에서 반응 속도를 높이기 위해 주기적 변수를 단축한다.

리스크 관리 모듈의 완성도 또한 중요한 최적화 방향이다. 단일 거래 리스크 제한, 연속 손실 보호, 최대 철회 제어 등과 같은 다층의 위험 제어 장치를 도입할 수 있다. 또한, 신호 강도 및 시장 환경의 동력에 따라 포지션 크기를 조정하는 포지션 관리 시스템을 도입하는 것을 고려할 수 있다.

기계학습 기술의 응용은 또한 유망한 최적화 방향이다. 기계학습 알고리즘을 사용하여 매개 변수 선택, 신호 필터링 및 위험 제어를 최적화 할 수 있다. 예를 들어, 유전 알고리즘을 사용하여 매개 변수 조합을 최적화하거나, 지원 벡터 기계를 사용하여 신호 분류를 수행하거나, 강도 학습을 사용하여 동적 포지션 관리를 수행한다.

요약하다

듀얼 간격 파동 동향 추적 전략은 정교하게 설계된, 논리적으로 명확한 트렌드 추적 시스템이다. 그것의 핵심 장점은 듀얼 간격 메커니즘과 적응 간격 조정으로 트렌드 변화에 민감성을 유지하면서도 시장 소음을 효과적으로 필터링한다는 것이다. 전략의 듀얼 확인 메커니즘과 연속 카운트 논리는 신호 품질을 크게 향상시켜 트렌드 시장에서 좋은 성능을 얻을 수 있게 한다.

그러나, 전략은 또한 몇 가지 제한이 있습니다, 주로 흔들리는 시장에서의 적응력과 트렌드 전환 때 지연의 문제로 나타납니다. 이러한 문제는 해결할 수 없습니다. 시장 환경 인식, 동적 파라미터 조정 및 다단계 위험 제어와 같은 최적화 조치를 도입함으로써 전략의 전반적인 성능을 더욱 향상시킬 수 있습니다.

이 전략은 기술 분석 기초와 위험 관리 경험이있는 거래자의 사용에 특히 적합합니다. 실제 응용에서 다른 기술 지표와 기본 분석을 결합하여 더 완벽한 거래 시스템을 형성하는 것이 좋습니다. 또한, 역사 회귀 및 시뮬레이션 거래가 충분히 수행되어 전략의 다양한 시장 환경에서 수행 특성을 깊이 이해하고 그에 따른 위험 제어 조치를 수립해야합니다.

이 전략은 양적 거래자에게는 더 많은 혁신과 최적화를 위한 훌륭한 기본 프레임 워크를 제공합니다. 지속적인 연구와 개선으로 이 전략은 안정적이고 신뢰할 수 있는 양적 거래 도구가 될 잠재력을 가지고 있습니다.