Nota: Kes ini hanya digunakan untuk tujuan kajian dan bukan sebagai cadangan pelaburan.

Data harga bitcoin adalah berdasarkan urutan masa, oleh itu harga bitcoin diramalkan menggunakan model LSTM.

Memori jangka pendek jangka panjang (LSTM) adalah model pembelajaran mendalam yang sangat sesuai untuk data urutan masa (atau data yang mempunyai urutan masa / ruang / struktur, seperti filem, ayat, dan lain-lain) dan merupakan model yang ideal untuk meramalkan arah harga cryptocurrency.

Artikel ini ditulis terutamanya mengenai data yang disatukan melalui LSTM untuk meramalkan harga masa depan Bitcoin.

Perpustakaan yang diperlukan untuk import

import pandas as pd
import numpy as np

from sklearn.preprocessing import MinMaxScaler, LabelEncoder
from keras.models import Sequential
from keras.layers import LSTM, Dense, Dropout

from matplotlib import pyplot as plt
%matplotlib inline

Analisis data

Muat naik data

Baca data dagangan harian BTC

data = pd.read_csv(filepath_or_buffer="btc_data_day")

Terdapat 1380 data yang terdiri daripada tarikh, buka, tinggi, rendah, tutup, jumlah (BTC), jumlah (mata wang), dan harga berat.

data.info()

Lihat 10 baris pertama.

data.head(10)

Visualisasi data

Matplotlib digunakan untuk memetakan harga tertimbang dan melihat bagaimana ia diedarkan. Di dalam grafik, terdapat bahagian data 0 yang perlu kita pastikan terdapat pengecualian.

plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()

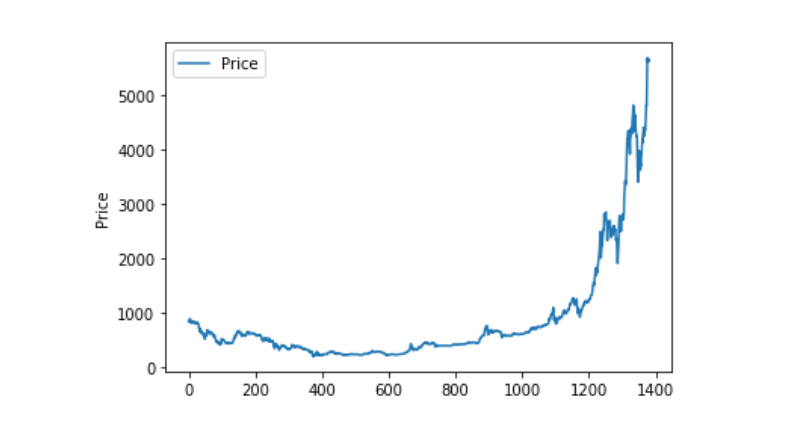
Pemprosesan data yang tidak normal

Anda boleh lihat jika terdapat data yang mengandungi nan dan anda boleh lihat jika terdapat data yang tidak mengandungi nan.

data.isnull().sum()

Date                 0
Open                 0
High                 0
Low                  0
Close                0
Volume (BTC)         0
Volume (Currency)    0
Weighted Price       0
dtype: int64

Kemudian kita lihat data sifar, kita dapat lihat bahawa data kita mengandungi nilai sifar, dan kita perlu melakukan sesuatu terhadap nilai sifar.

(data == 0).astype(int).any()

Date                 False
Open                  True
High                  True
Low                   True
Close                 True
Volume (BTC)          True
Volume (Currency)     True
Weighted Price        True
dtype: bool

data['Weighted Price'].replace(0, np.nan, inplace=True)
data['Weighted Price'].fillna(method='ffill', inplace=True)
data['Open'].replace(0, np.nan, inplace=True)
data['Open'].fillna(method='ffill', inplace=True)
data['High'].replace(0, np.nan, inplace=True)
data['High'].fillna(method='ffill', inplace=True)
data['Low'].replace(0, np.nan, inplace=True)
data['Low'].fillna(method='ffill', inplace=True)
data['Close'].replace(0, np.nan, inplace=True)
data['Close'].fillna(method='ffill', inplace=True)
data['Volume (BTC)'].replace(0, np.nan, inplace=True)
data['Volume (BTC)'].fillna(method='ffill', inplace=True)
data['Volume (Currency)'].replace(0, np.nan, inplace=True)
data['Volume (Currency)'].fillna(method='ffill', inplace=True)

(data == 0).astype(int).any()

Date                 False
Open                 False
High                 False
Low                  False
Close                False
Volume (BTC)         False
Volume (Currency)    False
Weighted Price       False
dtype: bool

Dan kemudian kita lihat pada peredaran dan pergerakan data, di mana pada masa ini, ia sangat berterusan.

plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()

Pembahagian set data latihan dan set data ujian

Menggabungkan data ke 0-1

data_set = data.drop('Date', axis=1).values
data_set = data_set.astype('float32')
mms = MinMaxScaler(feature_range=(0, 1))
data_set = mms.fit_transform(data_set)

Bahagikan dataset ujian dan dataset latihan dengan 2:8

ratio = 0.8
train_size = int(len(data_set) * ratio)
test_size = len(data_set) - train_size
train, test = data_set[0:train_size,:], data_set[train_size:len(data_set),:]

Buat set data latihan dan set data ujian dengan satu hari sebagai tempoh tetingkap untuk mencipta set data latihan dan set data ujian kami.

def create_dataset(data):
    window = 1
    label_index = 6
    x, y = [], []
    for i in range(len(data) - window):
        x.append(data[i:(i + window), :])
        y.append(data[i + window, label_index])
    return np.array(x), np.array(y)

train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)

Mendefinisikan dan melatih model

Kali ini kita akan menggunakan model yang mudah, dan model ini mempunyai struktur seperti berikut:. LSTM2. Dense。

Input Shape mempunyai dimensi input sebagai ((batch_size, time steps, features)). Di sini, nilai langkah masa adalah selang waktu tetingkap ketika data dimasukkan, di sini kita menggunakan 1 hari sebagai tetingkap masa, dan data kita adalah data harian, jadi langkah masa kita adalah 1

Memori jangka pendek panjang (LSTM) adalah sejenis RNN khas yang digunakan untuk menyelesaikan masalah kehilangan gradien dan letupan gradien semasa latihan urutan panjang.

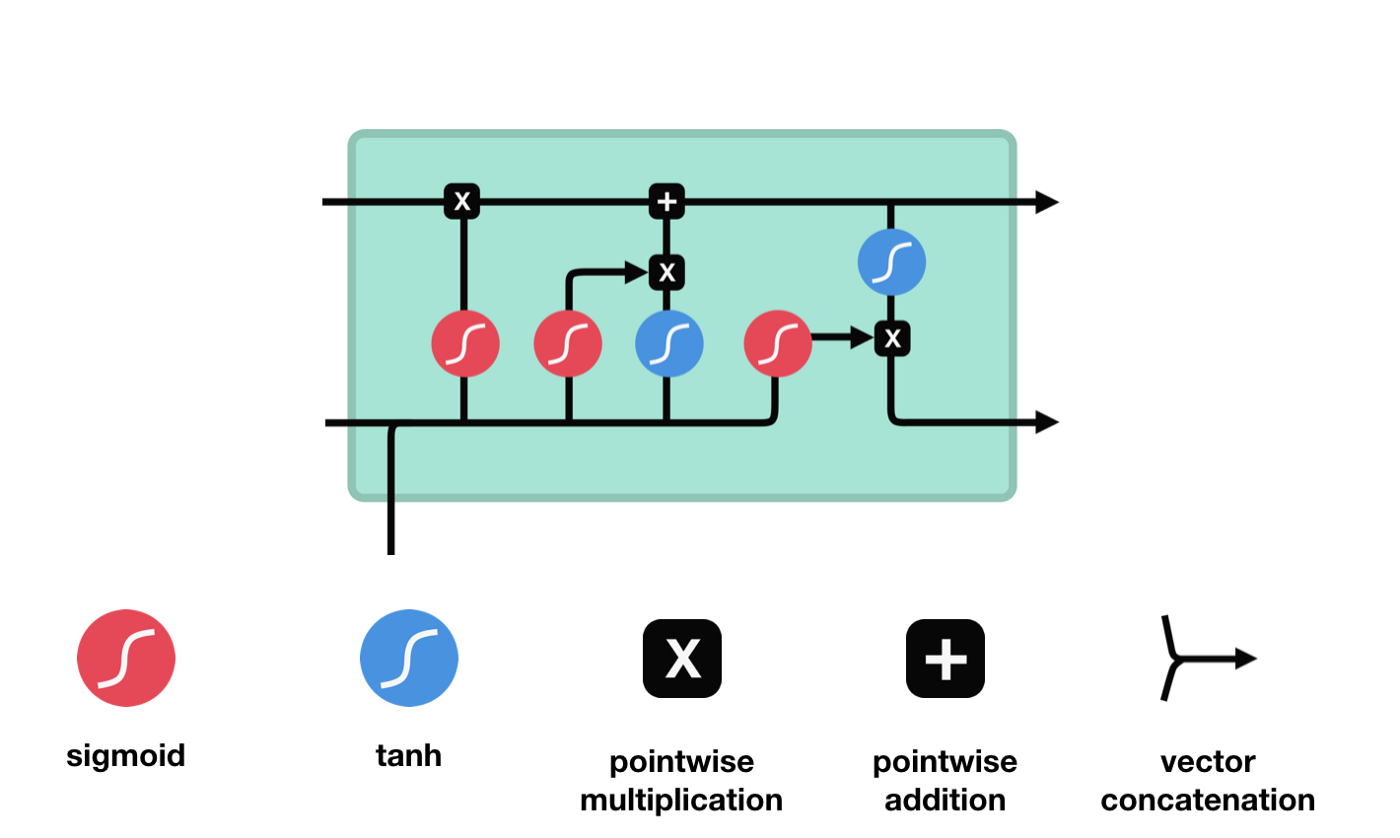
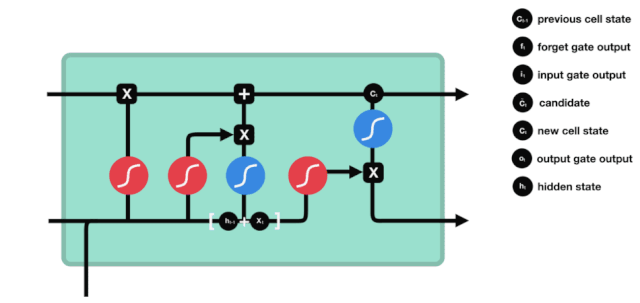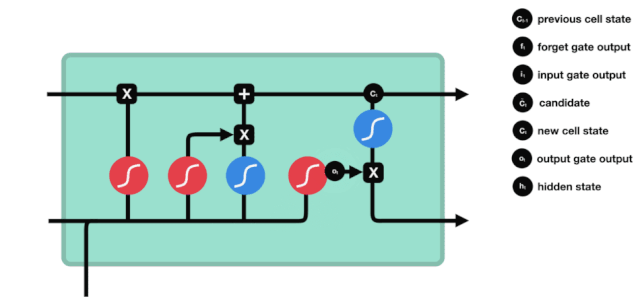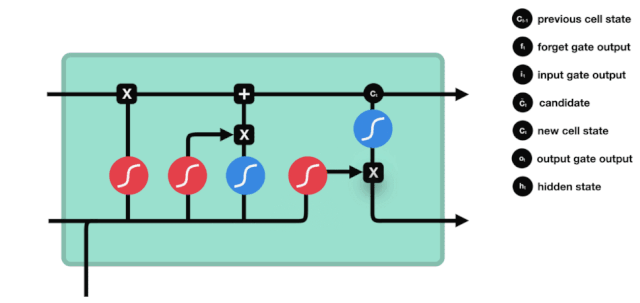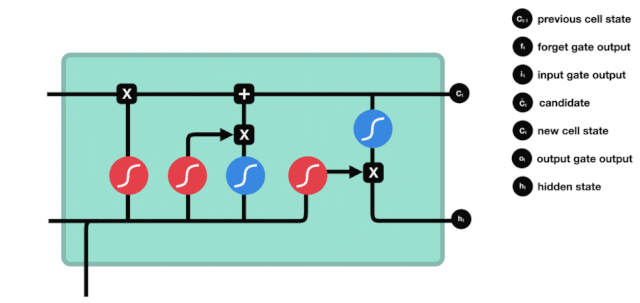
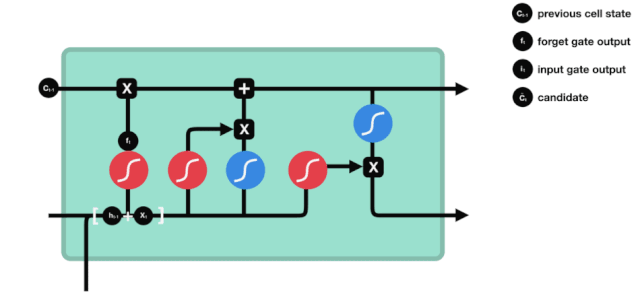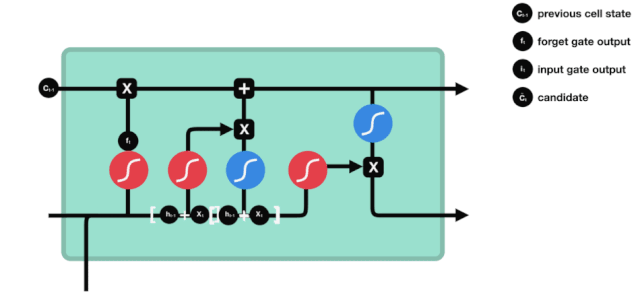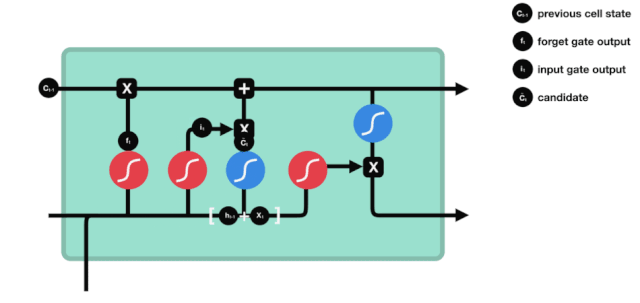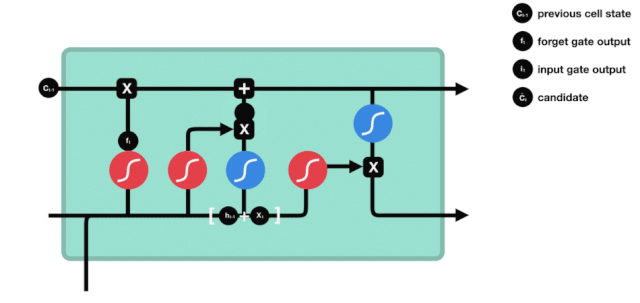
Dari diagram struktur rangkaian LSTM, dapat dilihat bahawa LSTM sebenarnya adalah model kecil yang mengandungi 3 fungsi pengaktifan sigmoid, 2 fungsi pengaktifan tanh, 3 penggandaan dan 1 penambahan.

Status sel

Keadaan sel adalah pusat LSTM, ia adalah garis hitam di bahagian atas dalam gambar di atas, di bawah garis hitam ini terdapat beberapa pintu, yang akan kami jelaskan di bawah. Keadaan sel akan dikemas kini mengikut hasil setiap pintu. Di bawah ini kami akan memperkenalkan pintu-pintu ini, anda akan memahami proses keadaan sel.

Rangkaian LSTM dapat menghapuskan atau menambah maklumat mengenai keadaan sel melalui struktur yang dikenali sebagai pintu. Pintu dapat membuat keputusan pilihan mengenai maklumat mana yang boleh dilalui. Struktur pintu adalah gabungan lapisan sigmoid dan operasi penggandaan titik. Oleh kerana output lapisan sigmoid adalah nilai 0-1, 0 tidak dapat dilalui, 1 dapat dilalui.

Pintu Lupakan

Langkah pertama LSTM adalah untuk menentukan maklumat yang perlu dibuang oleh keadaan sel. Operasi ini dilakukan melalui unit sigmoid yang dikenali sebagai pintu lupa.

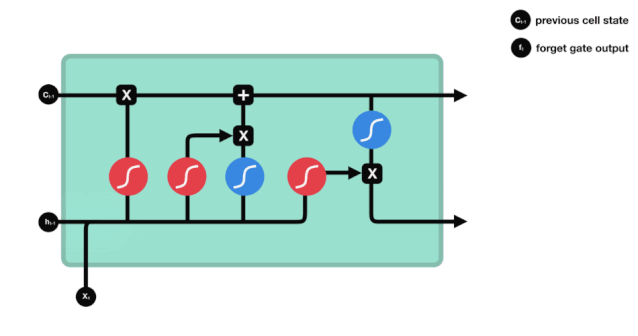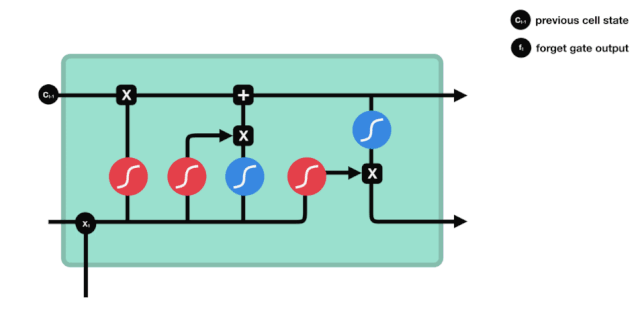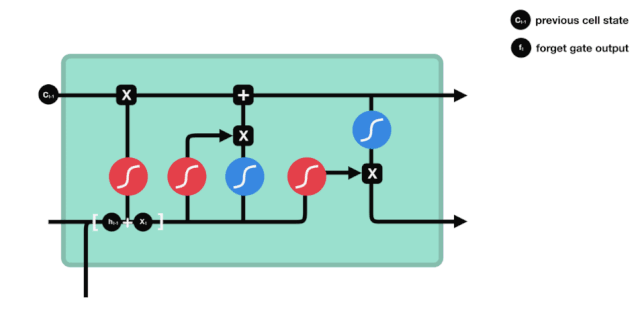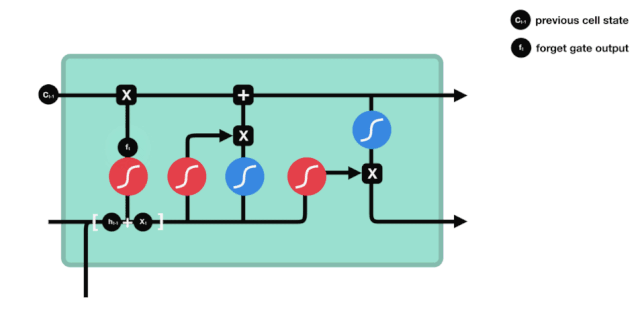
Kita dapat melihat bahawa pintu lupa akan melihat maklumat \(h_{l-1}\) dan \(x_{t}\) untuk menghasilkan vektor antara 0 - 1, nilai 0 - 1 dalam vektor ini menunjukkan berapa banyak maklumat yang disimpan atau dibuang dalam keadaan sel \(C_{t-1}\). 0 menunjukkan tidak disimpan, dan 1 menunjukkan disimpan.

Ungkapan matematik: \(f_{t} =\sigma\left(W_{f} \cdot\left[h_{t-1}, x_{t}\right]+b_{f}\right)\)

Pintu masuk

Langkah seterusnya ialah memutuskan apa maklumat baru yang akan ditambahkan kepada status sel, dan langkah ini dilakukan dengan membuka pintu masuk.

Kita lihat \(h_{l-1}\) dan \(x_{t}\) dimasukkan ke dalam sebuah gerbang lupa (sigmoid) dan gerbang input (tanh). Oleh kerana output gerbang lupa adalah nilai 0-1, oleh itu, jika gerbang lupa mengeluarkan nilai 0, hasilnya \(C_{i}\) tidak akan ditambahkan ke dalam keadaan sel semasa, jika 1, semuanya akan ditambahkan ke dalam keadaan sel, oleh itu fungsi gerbang lupa di sini adalah untuk menambahkan hasil input gerbang secara terpilih ke dalam keadaan sel.

Formula matematik ialah: \(C_{t}=f_{t} * C_{t-1}+i_{t} *\tilde{C}_{t}\)

Pintu keluar

Selepas mengemas kini keadaan sel diperlukan untuk menilai ciri-ciri keadaan sel output berdasarkan jumlah \( h_ {l-1} \) dan \( x_ {t} \) input, di mana input perlu dinilai melalui lapisan sigmoid yang dipanggil pintu keluar, dan kemudian keadaan sel melalui lapisan tanh untuk mendapatkan nilai antara -1 ~ 1 vektor, yang berganda dengan pintu keluar untuk mendapatkan output unit RNN akhir.

def create_model():
    model = Sequential()
    model.add(LSTM(50, input_shape=(train_x.shape[1], train_x.shape[2])))
    model.add(Dense(1))
    model.compile(loss='mae', optimizer='adam')
    model.summary()
    return model

model = create_model()

history = model.fit(train_x, train_y, epochs=80, batch_size=64, validation_data=(test_x, test_y), verbose=1, shuffle=False)

plt.plot(history.history['loss'], label='train')
plt.plot(history.history['val_loss'], label='test')
plt.legend()
plt.show()

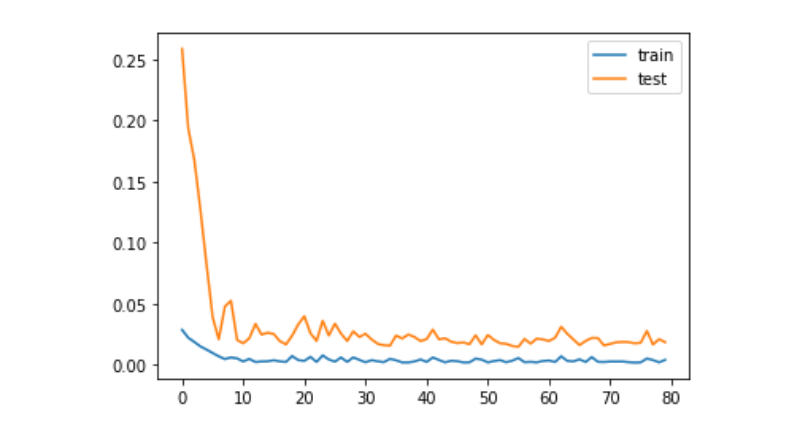
train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)

Ramalan

predict = model.predict(test_x)
plt.plot(predict, label='predict')
plt.plot(test_y, label='ground true')
plt.legend()
plt.show()

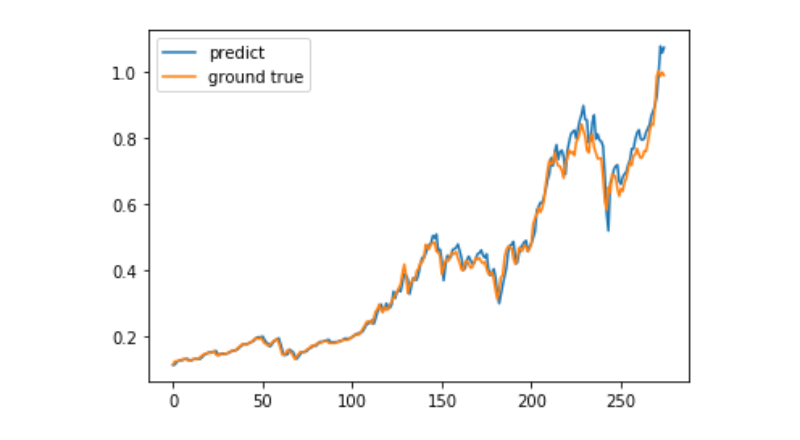
Pada masa ini, penggunaan pembelajaran mesin untuk meramalkan pergerakan harga jangka panjang Bitcoin masih sangat sukar, dan artikel ini hanya boleh digunakan sebagai kes pembelajaran. Kes ini akan dimuat naik dan pengguna yang berminat boleh mengalaminya secara langsung dalam gambar demo dari Matrix Cloud.