Nota: Este caso é apenas para fins de estudo e pesquisa e não constitui uma recomendação de investimento.

Os dados de preços do Bitcoin são baseados em sequências temporais, portanto, a previsão de preços do Bitcoin é realizada principalmente com o modelo LSTM.

A memória de curto e longo prazo (LSTM) é um modelo de aprendizado profundo especialmente adequado para dados de sequência temporal (ou dados com sequência temporal / espacial / estruturada, como filmes, sentenças, etc.) e é o modelo ideal para prever a direção dos preços das criptomoedas.

Este artigo é escrito principalmente sobre a comparação de dados com o LSTM para a previsão do preço futuro do Bitcoin.

Repositório importado

import pandas as pd
import numpy as np

from sklearn.preprocessing import MinMaxScaler, LabelEncoder
from keras.models import Sequential
from keras.layers import LSTM, Dense, Dropout

from matplotlib import pyplot as plt
%matplotlib inline

Análise de dados

Carregamento de dados

Leia dados de transações diárias do BTC

data = pd.read_csv(filepath_or_buffer="btc_data_day")

Os dados disponíveis são os seguintes: Data, Aberto, Alto, Baixo, Fecho, Volume (BTC), Volume (Currency) e Preço ponderado. Exceto a coluna Data, as colunas restantes são do tipo de dados float64.

data.info()

Veja as primeiras 10 linhas de dados.

data.head(10)

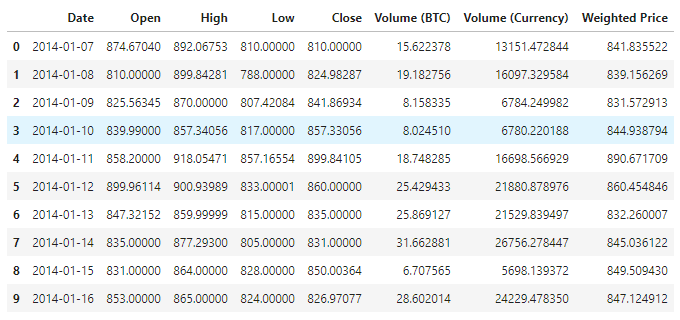
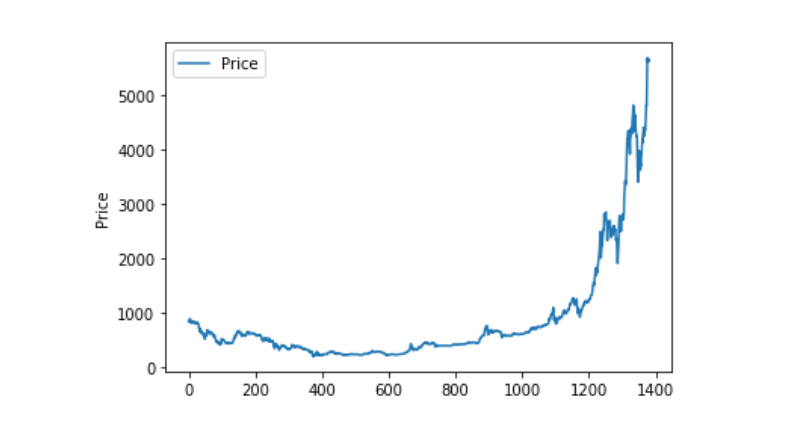
Visualização de dados

Use o matplotlib para mapear o preço ponderado e ver a distribuição e a evolução dos dados. No gráfico, encontramos uma parte do dado 0 e precisamos confirmar se há alguma exceção nos dados.

plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()

Processamento de dados anormal

Primeiro, vamos ver se os dados contêm dados de nanos, e podemos ver que não temos dados de nanos.

data.isnull().sum()

Date                 0
Open                 0
High                 0
Low                  0
Close                0
Volume (BTC)         0
Volume (Currency)    0
Weighted Price       0
dtype: int64

Então vamos olhar para os dados 0 e veremos que eles contêm valores 0 e nós temos que lidar com esses valores.

(data == 0).astype(int).any()

Date                 False
Open                  True
High                  True
Low                   True
Close                 True
Volume (BTC)          True
Volume (Currency)     True
Weighted Price        True
dtype: bool

data['Weighted Price'].replace(0, np.nan, inplace=True)
data['Weighted Price'].fillna(method='ffill', inplace=True)
data['Open'].replace(0, np.nan, inplace=True)
data['Open'].fillna(method='ffill', inplace=True)
data['High'].replace(0, np.nan, inplace=True)
data['High'].fillna(method='ffill', inplace=True)
data['Low'].replace(0, np.nan, inplace=True)
data['Low'].fillna(method='ffill', inplace=True)
data['Close'].replace(0, np.nan, inplace=True)
data['Close'].fillna(method='ffill', inplace=True)
data['Volume (BTC)'].replace(0, np.nan, inplace=True)
data['Volume (BTC)'].fillna(method='ffill', inplace=True)
data['Volume (Currency)'].replace(0, np.nan, inplace=True)
data['Volume (Currency)'].fillna(method='ffill', inplace=True)

(data == 0).astype(int).any()

Date                 False
Open                 False
High                 False
Low                  False
Close                False
Volume (BTC)         False
Volume (Currency)    False
Weighted Price       False
dtype: bool

Então, olhando para a distribuição dos dados e para a evolução, a curva é muito contínua.

plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()

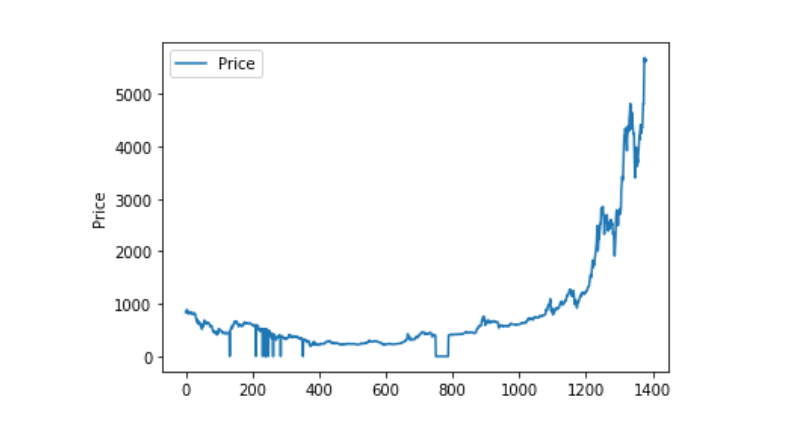
Divisão entre o conjunto de dados de treinamento e o conjunto de dados de teste

Reunificação de dados para 0-1

data_set = data.drop('Date', axis=1).values
data_set = data_set.astype('float32')
mms = MinMaxScaler(feature_range=(0, 1))
data_set = mms.fit_transform(data_set)

Dividir o conjunto de dados de teste e o conjunto de dados de treinamento por 2:8

ratio = 0.8
train_size = int(len(data_set) * ratio)
test_size = len(data_set) - train_size
train, test = data_set[0:train_size,:], data_set[train_size:len(data_set),:]

Criar um conjunto de dados de treinamento e testes com um dia como período de janela para criar o nosso conjunto de dados de treinamento e testes.

def create_dataset(data):
    window = 1
    label_index = 6
    x, y = [], []
    for i in range(len(data) - window):
        x.append(data[i:(i + window), :])
        y.append(data[i + window, label_index])
    return np.array(x), np.array(y)

train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)

Definição e treino do modelo

E nós usamos um modelo simples, que é construído da seguinte forma:. LSTM2. Dense。

Aqui, o valor de time steps é o intervalo da janela de tempo no momento em que os dados são inseridos. Aqui, usamos 1 dia como janela de tempo, e nossos dados são dados diários, portanto, nossos passos de tempo são 1 .

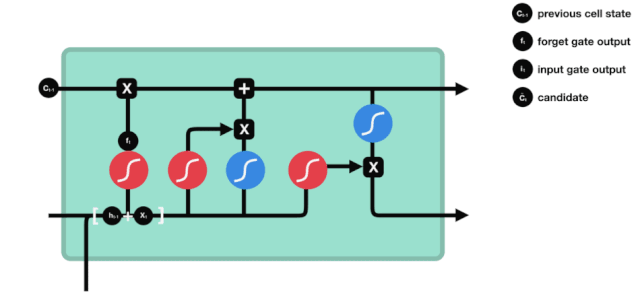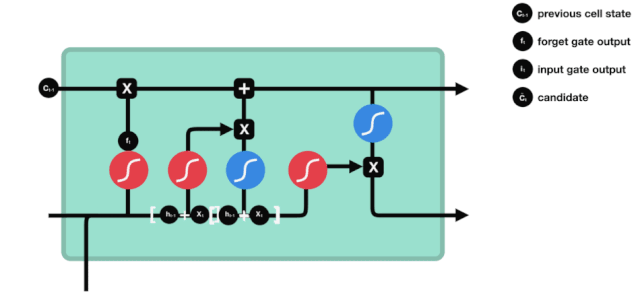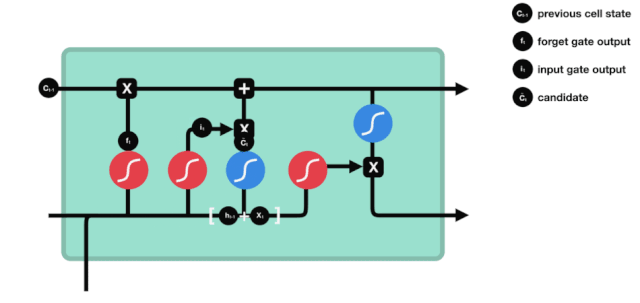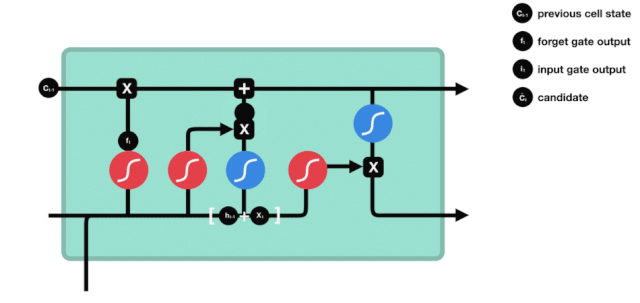
A memória de curto prazo (LSTM) é um tipo de RNN especial, principalmente para resolver o problema do desaparecimento de gradiente e explosão de gradiente durante o treinamento de sequências longas.

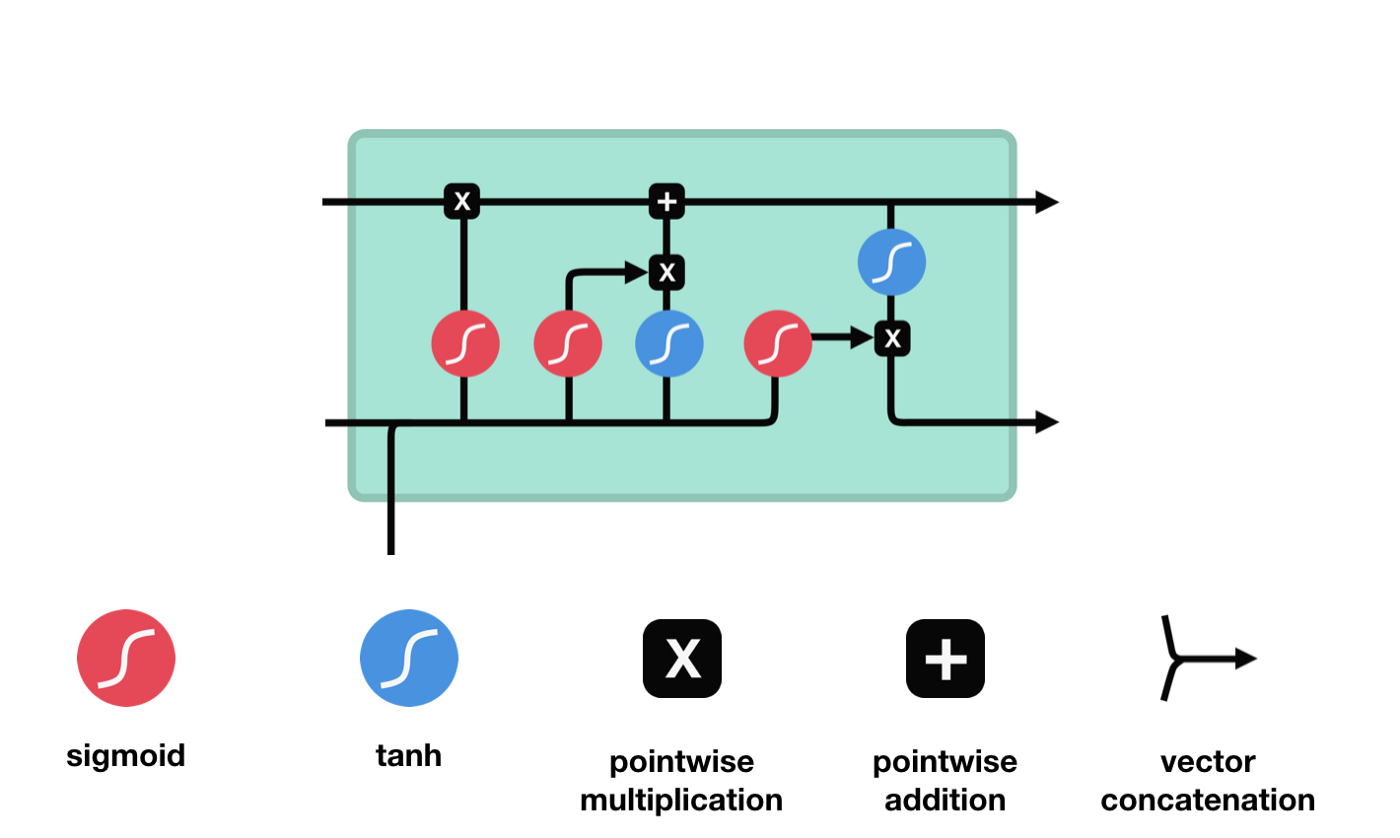
A partir do gráfico da estrutura da rede do LSTM, pode-se ver que o LSTM é, na verdade, um modelo pequeno que contém 3 funções de ativação sigmoide, 2 funções de ativação tanh, 3 multiplicações e 1 adição.

Estado celular

O estado celular é o núcleo do LSTM, ele é a linha preta no topo do gráfico acima, abaixo desta linha preta estão algumas portas, que nós descrevemos mais adiante. O estado celular será atualizado de acordo com o resultado de cada porta.

A rede LSTM é capaz de adicionar ou remover informações sobre o estado celular por meio de uma estrutura chamada portão. A porta é capaz de decidir seletivamente quais informações devem passar. A estrutura da porta é uma combinação de uma camada sigmoide e uma operação de multiplicação de pontos.

A porta do esquecimento

O primeiro passo do LSTM é decidir quais informações o estado celular precisa de descartar. Esta parte da operação é feita por uma unidade sigmoide chamada porta do esquecimento.

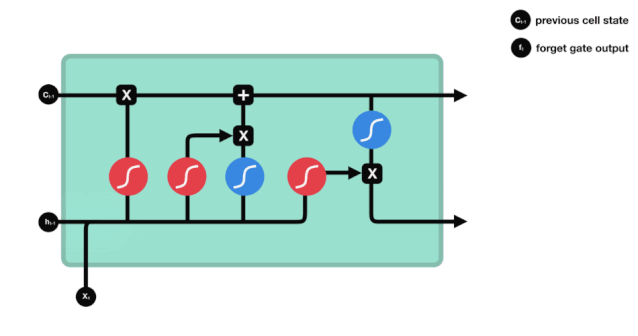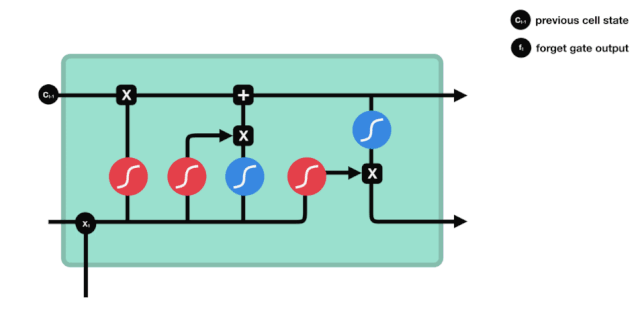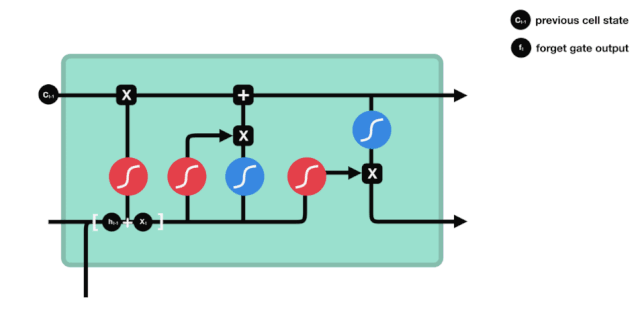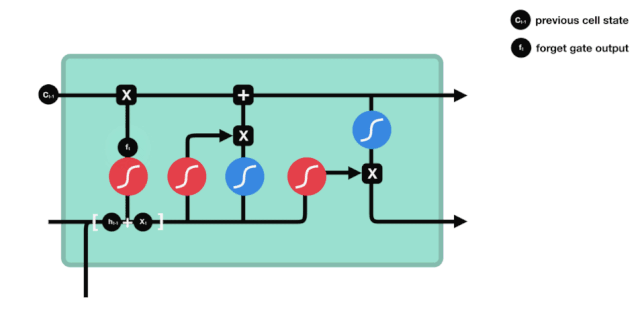
Podemos ver que o portal de esquecimento examina a informação \(h_{l-1}\) e \(x_{t}\) para expor um vetor entre 0-1 no qual o valor 0-1 indica o quanto de informação é mantida ou descartada no estado de célula \(C_{t-1}\). 0 indica que não é mantida e 1 indica que é mantida.

A expressão matemática: \(f_{t} =\sigma\left(W_{f} \cdot\left[h_{t-1}, x_{t}\right]+b_{f}\right)\)

Portas de entrada

O próximo passo é decidir quais novas informações serão adicionadas ao estado da célula, e isso é feito através da entrada e abertura da porta.

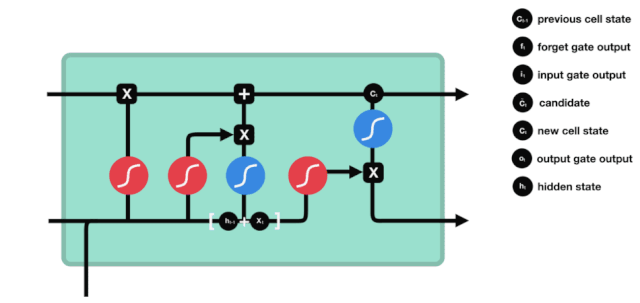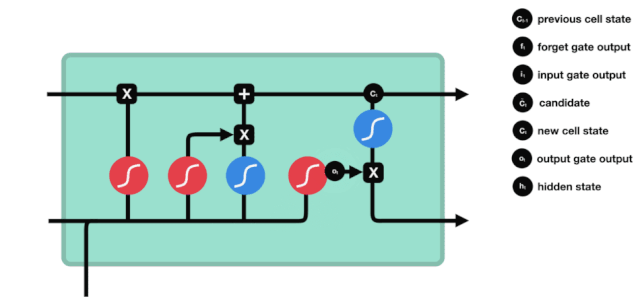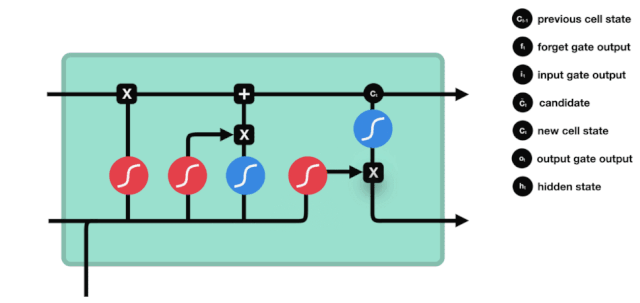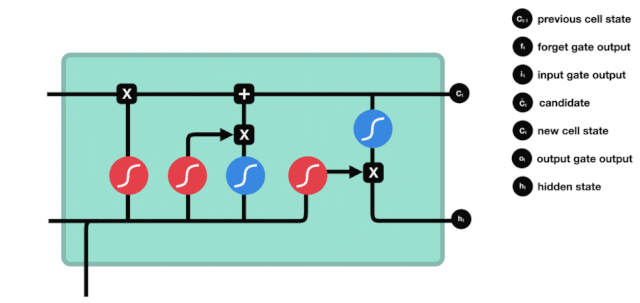
Vemos que \(h_{l-1}\) e \(x_{t}\) são inseridos em um portão de esquecimento (sigmoid) e um portão de entrada (tanh). Como o resultado do portão de esquecimento é 0-1, se o portão de esquecimento for 0, o resultado do portão de entrada \(C_{i}\) não será adicionado ao estado da célula atual, se for 1, tudo será adicionado ao estado da célula, então o portão de esquecimento aqui funciona como um resultado seletivo do portão de entrada adicionado ao estado da célula.

A fórmula matemática é: \(C_{t}=f_{t} * C_{t-1}+i_{t} *\tilde{C}_{t}\)

Porta de saída

A atualização do estado da célula requer a soma das entradas \(h_{l-1}\) e \(x_{t}\) para determinar quais características do estado da célula de saída. Aqui, a entrada é determinada por uma camada sigmoide chamada porta de saída, e a entrada é determinada por uma camada tanh com um vector de valor entre -1 e 1, multiplicado pela entrada de saída, obtendo a saída final da unidade RNN.

def create_model():
    model = Sequential()
    model.add(LSTM(50, input_shape=(train_x.shape[1], train_x.shape[2])))
    model.add(Dense(1))
    model.compile(loss='mae', optimizer='adam')
    model.summary()
    return model

model = create_model()

history = model.fit(train_x, train_y, epochs=80, batch_size=64, validation_data=(test_x, test_y), verbose=1, shuffle=False)

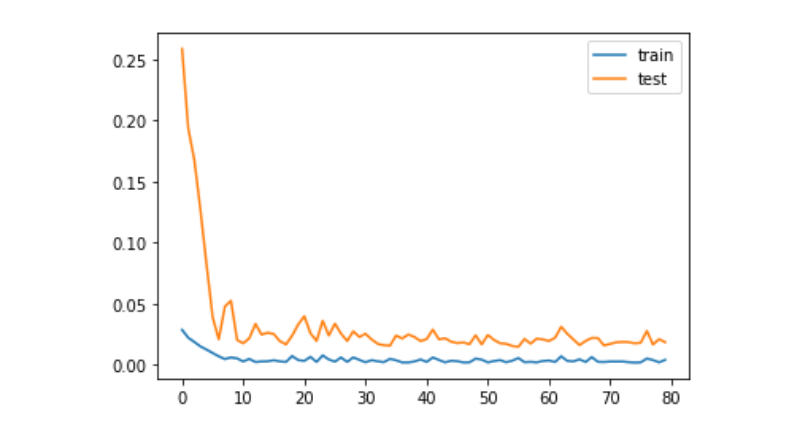
plt.plot(history.history['loss'], label='train')
plt.plot(history.history['val_loss'], label='test')
plt.legend()
plt.show()

train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)

Previsões

predict = model.predict(test_x)
plt.plot(predict, label='predict')
plt.plot(test_y, label='ground true')
plt.legend()
plt.show()

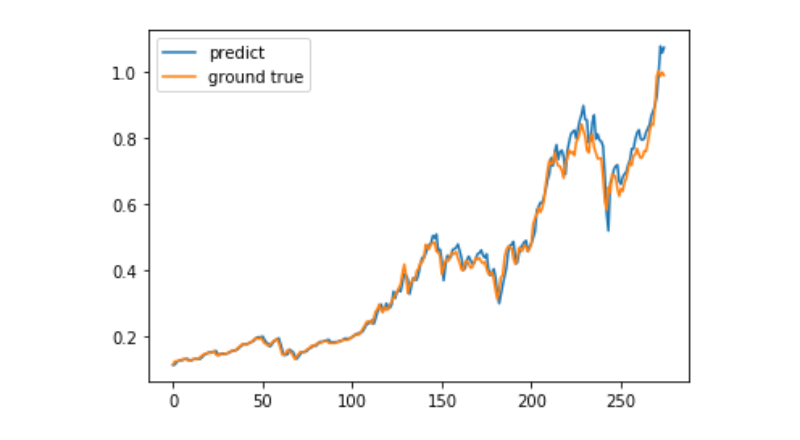
Atualmente, o uso de aprendizagem de máquina para prever a movimentação de preços de longo prazo do Bitcoin ainda é muito difícil. Este artigo pode ser usado apenas como um caso de estudo.