A estatística bayesiana é uma disciplina poderosa na matemática com amplas aplicações em muitos campos, incluindo finanças, pesquisa médica e tecnologia da informação. Ela nos permite combinar crenças anteriores com evidências para chegar a novas crenças posteriores, permitindo-nos tomar decisões mais informadas.

Neste artigo, apresentaremos brevemente alguns dos principais matemáticos que fundaram esse campo.

Antes de Bayes Para entender melhor as estatísticas bayesianas, precisamos voltar ao século XVIII e consultar o matemático De Moivre e seu artigo “O Princípio do Acaso”.[1]。

Em seu tratado, De Moivre abordou muitos dos problemas de sua época relacionados à probabilidade e ao jogo. Como você provavelmente sabe, a solução dele para um desses problemas levou à origem da distribuição normal, mas essa é outra história.

Em seu artigo há uma pergunta simples:

“A probabilidade de obter três caras ao lançar uma moeda honesta três vezes seguidas.”

Lendo os problemas descritos em “O Princípio do Acaso”, você pode perceber que a maioria deles começa com uma hipótese a partir da qual a probabilidade de um determinado evento é calculada. Por exemplo, no problema acima, há uma suposição de que a moeda é honesta, então a probabilidade de obter cara no lançamento é de 0,5.

Hoje isso é expresso em termos matemáticos como:

𝑃(𝑋|𝜃)

Mas e se não soubermos se a moeda é honesta? Se não sabemos𝜃Tecido de lã?

Thomas Bayes e Richard Price

Quase cinquenta anos depois, em 1763, um artigo intitulado “Um ensaio sobre o princípio do acaso”[2] Publicado nas Philosophical Transactions da Royal Society de Londres.

Nas primeiras páginas do documento, há um texto escrito pelo matemático Richard Price resumindo o conteúdo de um artigo escrito por seu amigo Thomas Bayes alguns anos antes de sua morte. Na introdução, Price explica a importância de algumas descobertas feitas por Thomas Bayes que não foram abordadas nos Princípios do Acaso de De Moivre.

Na verdade, ele estava se referindo a um problema específico:

“Dado o número de ocorrências e falhas de um evento desconhecido, encontre a chance de sua ocorrência estar entre quaisquer dois graus de probabilidade nomeados.”

Em outras palavras, após observar um evento, encontramos o parâmetro desconhecidoθQual é a probabilidade entre dois graus de probabilidade? Este é, na verdade, um dos primeiros problemas da história relacionados à inferência estatística e deu origem ao nome probabilidade inversa. Em termos matemáticos:

𝑃( 𝜃 | 𝑋）

É claro que isso é o que hoje chamamos de distribuição posterior do teorema de Bayes.

Causas não causadas

Conheça esses dois pastores mais velhos.Thomas BayesePreço de Richard, o que motivou a pesquisa é realmente muito interessante. Mas para fazer isso, precisamos deixar de lado alguns conhecimentos sobre estatística por um momento.

Estamos no século XVIII, e a probabilidade está se tornando uma área de interesse crescente para os matemáticos. Matemáticos como De Moivre ou Bernoulli mostraram que alguns eventos ocorrem com um certo grau de aleatoriedade, mas ainda são governados por regras fixas. Por exemplo, se você rolar um dado muitas vezes, uma em cada seis vezes ele cairá em um seis. É como se houvesse uma regra oculta que determina o destino do acaso.

Agora, imagine que você é um matemático e um crente devoto vivendo neste período. Talvez você esteja interessado em saber como essa regra oculta se relaciona com Deus.

Essa é de fato a pergunta que os próprios Bayes e Price fizeram. A solução que eles esperavam para resolver esse problema era diretamente aplicável à prova de que “o mundo deve ser o resultado da sabedoria e da inteligência; fornecendo assim evidências da existência de Deus como causa final”.[2] - Ou seja, não há causa e efeito.

Laplace

Surpreendentemente, cerca de dois anos depois, em 1774, aparentemente sem ter lido o artigo de Thomas Bayes, o matemático francês Laplace escreveu um artigo intitulado “Sobre as causas dos eventos através das probabilidades dos eventos”.[3], que é um artigo sobre o problema da probabilidade inversa. Na primeira página você pode ler

Os princípios principais:

“Se um evento pode ser causado por n causas diferentes, então as probabilidades dessas causas para um dado evento estão em uma proporção igual à probabilidade do evento dada a causa, e a probabilidade da existência de cada uma dessas causas é igual para a probabilidade do evento dada a causa. A probabilidade das causas, dividida pela soma das probabilidades do evento dada cada uma dessas causas.”

Isto é o que conhecemos hoje como teorema de Bayes:

​

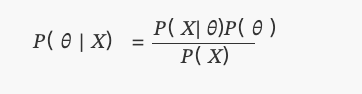
emP(θ)é uniformemente distribuído.

Experimento com moedas

Traremos as estatísticas bayesianas para o presente usando Python e a biblioteca PyMC e realizando um experimento simples.

Suponha que um amigo lhe dê uma moeda e pergunte se você acha que ela é honesta. Como ele está com pressa, ele diz para você jogar a moeda apenas 10 vezes. Como você pode ver, há um parâmetro desconhecido neste problemap, a probabilidade de obter cara no cara ou coroa, e queremos estimar issopO valor mais provável de .

(Nota: Não estamos falando de parâmetrospé uma variável aleatória, mas esse parâmetro é fixo e queremos saber entre quais valores ele tem mais probabilidade de estar. ）

Para obter uma perspectiva diferente sobre esse problema, abordaremos isso sob duas crenças anteriores diferentes:

• 1. Você não tem nenhuma informação prévia sobre a imparcialidade da moeda e atribui probabilidades iguais ap. Neste caso, usaremos o que é chamado de prior não informativo, porque você não está adicionando nenhuma informação à sua crença.
• 1. Você sabe por experiência que mesmo que uma moeda possa ser injusta, é difícil torná-la muito injusta, então você acha que os parâmetrospProvavelmente não ficará abaixo de 0,3 nem acima de 0,7. Neste caso, usaremos um prior informativo.

Para ambos os casos, nossas crenças anteriores serão as seguintes:

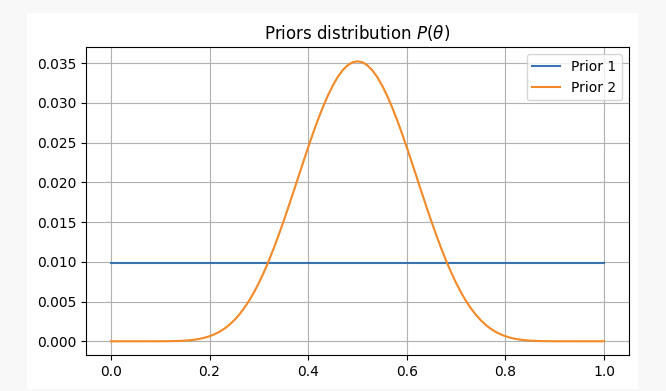
Depois de lançar uma moeda 10 vezes, você obtém 2 caras. Com essa evidência, provavelmente podemos descobrir onde encontrar nossos parâmetrosp？

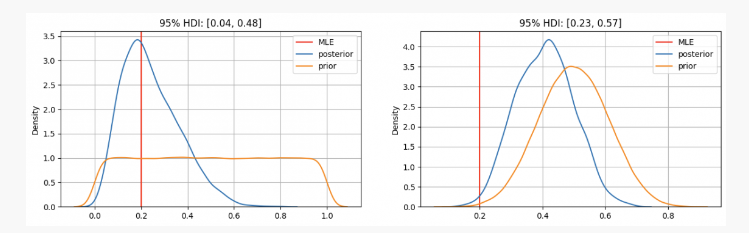
Como você pode ver, no primeiro caso temospA distribuição anterior é centrada na estimativa de máxima verossimilhança (MLE)p=0.2, que é uma abordagem semelhante usando o método frequentista. O verdadeiro parâmetro desconhecido estará dentro do intervalo de credibilidade de 95% entre 0,04 e 0,48.

Por outro lado, quando há alta confiança de que o parâmetrop Enquanto deveria estar entre 0,3 e 0,7, podemos ver que a distribuição posterior está em torno de 0,4, o que é muito maior do que o valor fornecido pelo nosso MLE. Nesse caso, o verdadeiro parâmetro desconhecido estará dentro do intervalo de credibilidade de 95% entre 0,23 e 0,57.

Então, no primeiro caso, você diria ao seu amigo que está confiante de que a moeda é injusta. Mas em outro caso, você diria a ele que não tem certeza se a moeda é honesta.

Como você pode ver, mesmo com as mesmas evidências (2 caras em 10 lançamentos), os resultados podem ser diferentes, dadas as diferentes crenças anteriores. Esse é um ponto forte da estatística bayesiana, que, semelhante ao método científico, nos permite atualizar nossas crenças combinando crenças anteriores com novas observações e evidências.

END

No artigo de hoje, vimos as origens da estatística bayesiana e seus principais contribuidores. Desde então, houve muitos outros colaboradores importantes neste campo da estatística (Jeffreys, Cox, Shannon, etc.), reproduzido de quantdare.com.