1. Breve introdução

Redes neurais profundas têm se tornado cada vez mais populares nos últimos anos, resolvendo problemas antes insolúveis em muitos campos e demonstrando suas poderosas capacidades. Na previsão de séries temporais, o preço de rede neural comumente usado é RNN, porque RNN não tem apenas entrada de dados atuais, mas também entrada de dados históricos. Claro, quando falamos sobre RNN prevendo preços, frequentemente falamos sobre um tipo de RNN : LSTM . Este artigo criará um modelo para prever preços de Bitcoin com base no pytorch. Embora haja muitas informações relevantes na Internet, elas ainda não são completas o suficiente, e há relativamente poucas pessoas usando o pytorch. Ainda é necessário escrever um artigo. O resultado final é usar o preço de abertura, preço de fechamento, maior preço, menor preço e volume de transações do mercado de Bitcoin. para prever o próximo preço de fechamento. Meu conhecimento pessoal sobre redes neurais é médio e agradeço suas críticas e correções. Este tutorial é produzido pela FMZ, a inventora da plataforma de negociação quantitativa de moeda digital (www.fmz.com). Bem-vindo ao grupo QQ: 863946592 para comunicação.

2. Dados e referências

Um exemplo de previsão de preço relacionado: https://yq.aliyun.com/articles/538484 Introdução detalhada ao modelo RNN: https://zhuanlan.zhihu.com/p/27485750 Compreendendo a entrada e a saída do RNN: https://www.zhihu.com/question/41949741/answer/318771336 Sobre o pytorch: Documentação oficial https://pytorch.org/docs Procure outras informações você mesmo. Além disso, alguns conhecimentos prévios são necessários para entender este artigo, como pandas/crawlers/processamento de dados, etc., mas não importa se você não sabe.

3. Parâmetros do modelo LSTM pytorch

Parâmetros do LSTM:

Quando vi pela primeira vez esses parâmetros densamente compactados no documento, minha reação foi: Conforme fui lendo devagar, finalmente entendi.

input_size: O tamanho do recurso do vetor de entrada x. Se o preço de fechamento for usado para prever o preço de fechamento, então input_size=1; se o preço de fechamento for previsto pela abertura máxima e fechamento mínima, então input_size=4 hidden_size: Tamanho da camada oculta num_layers: Número de camadas de RNN batch_first: Se True, a primeira dimensão de entrada é batch_size. Este parâmetro também é muito confuso e será descrito em detalhes abaixo.

Parâmetros de dados de entrada:

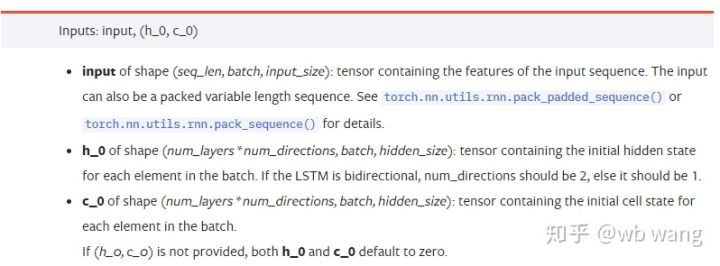
input: Os dados de entrada específicos são um tensor tridimensional com uma forma específica de (seq_len, batch, input_size). Entre eles, seq_len se refere ao comprimento da sequência, ou seja, quanto tempo os dados históricos LSTM precisam considerar. Observe que isso se refere apenas ao formato dos dados, não à estrutura interna do LSTM. O mesmo modelo LSTM pode dados de entrada com seq_len diferente e podem dar previsões. Resultado; batch refere-se ao tamanho do lote, que representa quantos grupos diferentes de dados existem; input_size é o input_size anterior. h_0: Estado oculto inicial, a forma é (num_layers * num_directions, batch, hidden_size), se for uma rede bidirecional num_directions=2 c_0: Estado inicial da célula, o formato é o mesmo acima, pode ser deixado sem especificação.

Parâmetros de saída:

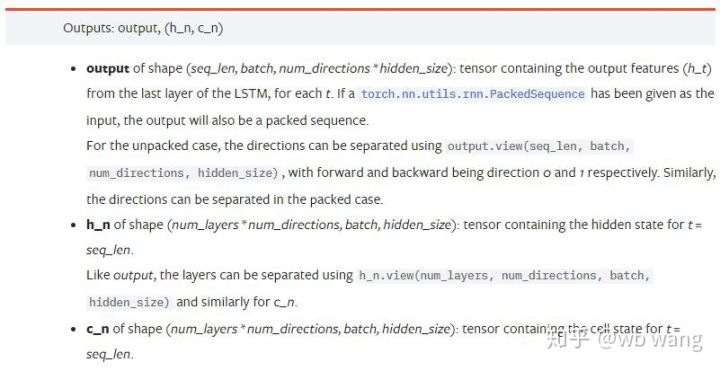
output: Formato de saída (seq_len, batch, num_directions * hidden_size), observe que está relacionado ao parâmetro do modelo batch_first h_n: h estado no tempo t = seq_len, mesma forma que h_0 c_n: c estado no tempo t = seq_len, mesma forma que c_0

4. Exemplo simples de entrada e saída LSTM

Primeiro importe os pacotes necessários

import pandas as pd
import numpy as np
import torch
import torch.nn as nn
import matplotlib.pyplot as plt

Definindo o modelo LSTM

LSTM = nn.LSTM(input_size=5, hidden_size=10, num_layers=2, batch_first=True)

Preparando dados de entrada

x = torch.randn(3,4,5)
# x的值为:
tensor([[[ 0.4657,  1.4398, -0.3479,  0.2685,  1.6903],
         [ 1.0738,  0.6283, -1.3682, -0.1002, -1.7200],
         [ 0.2836,  0.3013, -0.3373, -0.3271,  0.0375],
         [-0.8852,  1.8098, -1.7099, -0.5992, -0.1143]],

        [[ 0.6970,  0.6124, -0.1679,  0.8537, -0.1116],
         [ 0.1997, -0.1041, -0.4871,  0.8724,  1.2750],
         [ 1.9647, -0.3489,  0.7340,  1.3713,  0.3762],
         [ 0.4603, -1.6203, -0.6294, -0.1459, -0.0317]],

        [[-0.5309,  0.1540, -0.4613, -0.6425, -0.1957],
         [-1.9796, -0.1186, -0.2930, -0.2619, -0.4039],
         [-0.4453,  0.1987, -1.0775,  1.3212,  1.3577],
         [-0.5488,  0.6669, -0.2151,  0.9337, -1.1805]]])

A forma de x é (3,4,5), pois definimosbatch_first=True, neste momento, batch_size é 3, sqe_len é 4 e input_size é 5. x[0] representa o primeiro lote.

Se batch_first não for definido, o padrão será Falso, e os dados serão representados de forma completamente diferente, com um tamanho de lote de 4, sqe_len de 3 e input_size de 5. Neste momento x[0] representa os dados de todos os lotes em t=0, e assim por diante. Eu pessoalmente acho que essa configuração não é intuitiva, então adicionei o parâmetrobatch_first=True.

A conversão de dados entre os dois também é muito conveniente:x.permute(1,0,2)

Entrada e Saída

O formato da entrada e saída do LSTM é fácil de ser confundido, com a ajuda da figura a seguir para ajudar a entender:
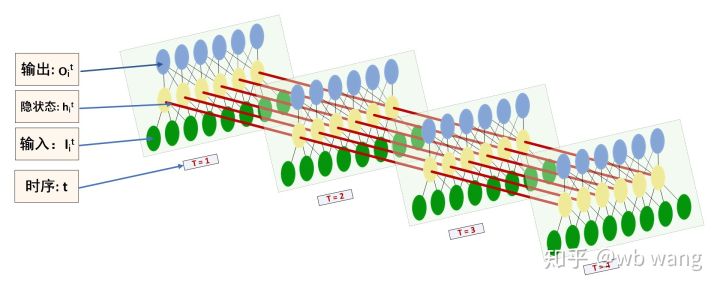
Fonte: https://www.zhihu.com/question/41949741/answer/318771336

x = torch.randn(3,4,5)
h0 = torch.randn(2, 3, 10)
c0 = torch.randn(2, 3, 10)
output, (hn, cn) = LSTM(x, (h0, c0))
print(output.size()) #在这里思考一下,如果batch_first=False输出的大小会是多少?
print(hn.size())
print(cn.size())
#结果
torch.Size([3, 4, 10])
torch.Size([2, 3, 10])
torch.Size([2, 3, 10])

Observe os resultados de saída, que são consistentes com a explicação do parâmetro anterior. Observe que o segundo valor de hn.size() é 3, o que é consistente com o tamanho de batch_size, indicando que nenhum estado intermediário é salvo em hn, apenas a última etapa. Como nossa rede LSTM tem duas camadas, a saída da última camada de hn é na verdade o valor da saída, e a forma da saída é[3, 4, 10], salva os resultados de todos os momentos t=0,1,2,3, então:

hn[-1][0] == output[0][-1] #第一个batch在hn最后一层的输出等于第一个batch在t=3时output的结果
hn[-1][1] == output[1][-1]
hn[-1][2] == output[2][-1]

5. Prepare os dados do mercado de Bitcoin

Muito do que eu disse antes é apenas um prelúdio. É muito importante entender a entrada e a saída do LSTM. Caso contrário, é fácil cometer erros se você copiar aleatoriamente alguns códigos da Internet. Devido à poderosa capacidade de LSTM em séries temporais, mesmo que o modelo esteja errado, você pode obtê-lo no final. Bons resultados.

Aquisição de dados

Os dados utilizados são os dados de mercado do par de negociação BTC_USD da bolsa Bitfinex.

import requests
import json

resp = requests.get('https://q.fmz.com/chart/history?symbol=bitfinex.btc_usd&resolution=15&from=0&to=0&from=1525622626&to=1562658565')
data = resp.json()
df = pd.DataFrame(data,columns = ['t','o','h','l','c','v'])
print(df.head(5))

O formato dos dados é o seguinte:

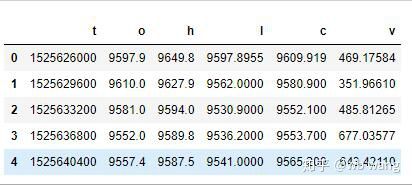
Pré-processamento de dados

df.index = df['t'] # index设为时间戳
df = (df-df.mean())/df.std() # 数据的标准化,否则模型的Loss会非常大,不利于收敛
df['n'] = df['c'].shift(-1) # n为下一个周期的收盘价,是我们预测的目标
df = df.dropna()
df = df.astype(np.float32) # 改变下数据格式适应pytorch

O método de padronização de dados é muito grosseiro e haverá alguns problemas. É apenas para demonstração. Você pode usar padronização de dados como yield.

Preparando dados de treinamento

seq_len = 10 # 输入10个周期的数据
train_size = 800 # 训练集batch_size
def create_dataset(data, seq_len):
    dataX, dataY=[], []
    for i in range(0,len(data)-seq_len, seq_len):
        dataX.append(data[['o','h','l','c','v']][i:i+seq_len].values)
        dataY.append(data['n'][i:i+seq_len].values)
    return np.array(dataX), np.array(dataY)
data_X, data_Y = create_dataset(df, seq_len)
train_x = torch.from_numpy(data_X[:train_size].reshape(-1,seq_len,5)) #变化形状,-1代表的值会自动计算
train_y = torch.from_numpy(data_Y[:train_size].reshape(-1,seq_len,1))

As formas finais de train_x e train_y são: torch.Size([800, 10, 5]), torch.Size([800, 10, 1]). Como nosso modelo prevê o preço de fechamento do próximo período com base em dados de 10 períodos, teoricamente, 800 lotes requerem apenas 800 preços de fechamento previstos. Mas train_y tem 10 dados em cada lote. Na verdade, os resultados intermediários de cada previsão de lote são retidos, não apenas o último. Ao calcular a Perda final, todos os 10 resultados de previsão podem ser levados em consideração e comparados com os valores reais em train_y. Teoricamente, também é possível calcular apenas a Perda do último resultado da previsão. Desenhei um diagrama aproximado para ilustrar esse problema. Como o modelo LSTM não contém realmente o parâmetro seq_len, o modelo pode ser aplicado a diferentes comprimentos, e os resultados de previsão intermediários também são significativos, então eu tendo a mesclar o cálculo de Perda.

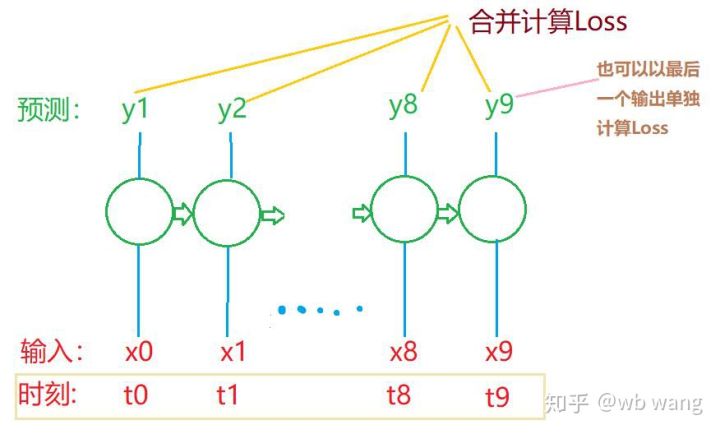
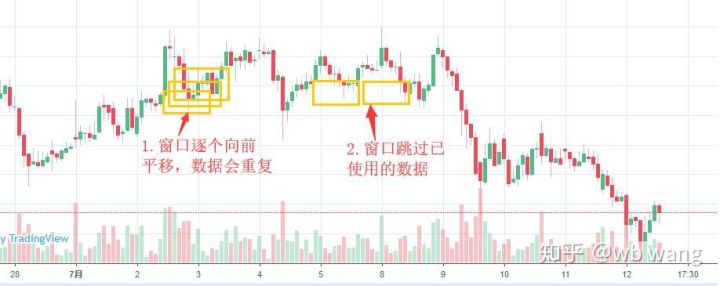
Note que ao preparar dados de treinamento, o movimento da janela é irregular, e os dados que foram usados ​​não são mais usados. Claro, as janelas também podem ser movidas uma a uma, de modo que o conjunto de treinamento obtido será muito maior . Mas senti que os dados do lote adjacente eram muito repetitivos, então adotei o método atual.

6. Construindo o modelo LSTM

O modelo final é o seguinte, que inclui um LSTM de duas camadas e uma camada Linear.

class LSTM(nn.Module):
    def __init__(self, input_size, hidden_size, output_size=1, num_layers=2):
        super(LSTM, self).__init__()
        self.rnn = nn.LSTM(input_size,hidden_size,num_layers,batch_first=True)
        self.reg = nn.Linear(hidden_size,output_size) # 线性层,把LSTM的结果输出成一个值

    def forward(self, x):
        x, _ = self.rnn(x) # 如果不理解前向传播中数据维度的变化,可单独调试
        x = self.reg(x)
        return x
        
net = LSTM(5, 10) # input_size为5,代表了高开低收和交易量. 隐含层为10.

7. Comece a treinar o modelo

Finalmente comecei o treinamento, o código é o seguinte:

criterion = nn.MSELoss() # 使用了简单的均方差损失函数
optimizer = torch.optim.Adam(net.parameters(),lr=0.01) # 优化函数,lr可调
for epoch in range(600): # 由于速度很快,这里的epoch多一些
    out = net(train_x) # 由于数据量很小, 直接拿全量数据计算
    loss = criterion(out, train_y)
    optimizer.zero_grad()
    loss.backward() # 反向传播损失
    optimizer.step() # 更新参数
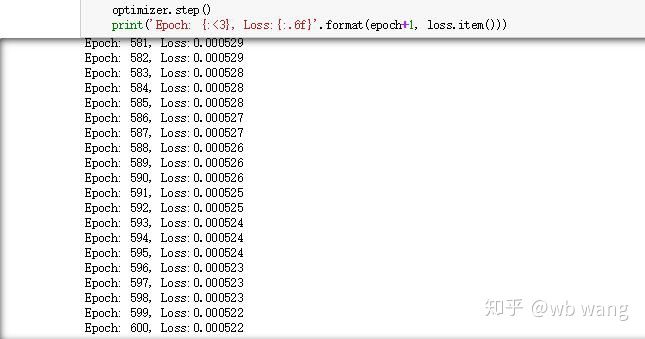
    print('Epoch: {:<3}, Loss:{:.6f}'.format(epoch+1, loss.item()))

Os resultados do treinamento são os seguintes:

8. Avaliação do modelo

Os valores previstos do modelo são:

p = net(torch.from_numpy(data_X))[:,-1,0] # 这里只取最后一个预测值作为比较
plt.figure(figsize=(12,8))
plt.plot(p.data.numpy(), label= 'predict')
plt.plot(data_Y[:,-1], label = 'real')
plt.legend()
plt.show()

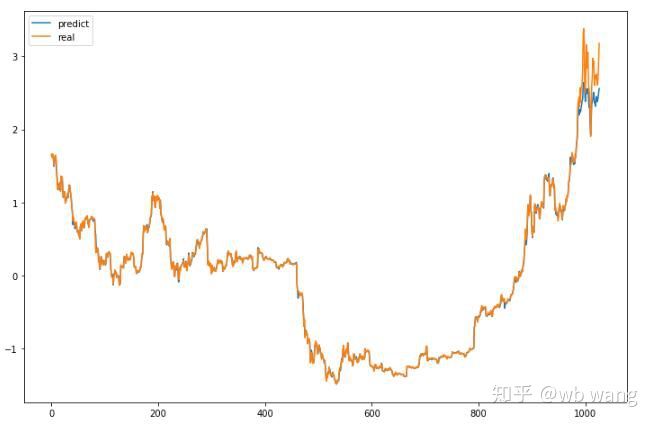
Como pode ser visto na figura, o grau de ajuste dos dados de treinamento (antes de 800) é muito alto, mas o preço do Bitcoin subiu para uma nova máxima posteriormente, e o modelo não viu esses dados, então a previsão é incapaz de ter um bom desempenho. Isso também mostra que havia um problema na padronização de dados anterior. Embora o preço previsto possa não ser preciso, quão precisa é a previsão da alta e queda? Dê uma olhada em uma seção dos dados de previsão:

r = data_Y[:,-1][800:1000]
y = p.data.numpy()[800:1000]
r_change = np.array([1 if i > 0 else 0 for i in r[1:200] - r[:199]])
y_change = np.array([1 if i > 0 else 0 for i in y[1:200] - r[:199]])
print((r_change == y_change).sum()/float(len(r_change)))

A precisão da previsão de subida e descida atingiu 81,4%, o que superou minhas expectativas. Não sei se cometi algum erro em algum lugar.

Claro, esse modelo não tem valor real, mas é simples e fácil de entender. Use isso apenas como um ponto de partida. Haverá mais cursos introdutórios sobre a aplicação de redes neurais na quantificação de moeda digital.