A classificação FMEX desbloqueia a otimização da quantidade ideal de pedidos
 0
0
 2308
2308

O colapso da FMEX causou muitos problemas para muitas pessoas, mas recentemente ela apresentou um plano de retomada e formulou regras semelhantes às da mineração original para desbloquear dívidas. Um artigo de análise foi fornecido sobre mineração de transações: https://www.fmz.com/bbs-topic/5834. Também há espaço para otimização na mineração de classificação. Embora as pessoas não devam cair no mesmo buraco duas vezes, aqueles que têm reivindicações sobre FMEX podem querer consultá-lo. Estratégias específicas em tempo real que podem ser executadas na plataforma quantitativa FMZ também podem ser lançadas.
Regras de desbloqueio de classificação FMEX
Defina cada 5 minutos de cada dia como um ciclo de desbloqueio de classificação, e cada ciclo recebe 1⁄288 da cota de desbloqueio de classificação do par de transações naquele dia. Em cada ciclo, um ponto de tempo aleatório é selecionado para tirar um instantâneo das ordens de compra e venda do par de negociação, onde:
- Compre 1 Com base na proporção do valor do pedido do usuário, 1⁄4 do valor de retorno do período de desbloqueio é alocado para esta classificação
- Venda 1 De acordo com a proporção do valor do pedido do usuário, 1⁄4 do valor de retorno do período de desbloqueio é alocado para esta classificação
- Para os 4 níveis de compra 2 a compra 5, 1⁄40 do valor de retorno do período de desbloqueio será alocado para cada nível de acordo com a proporção do valor do pedido do usuário em cada nível.
- Para os pedidos nos 4 níveis de venda 2 a venda 5, 1⁄40 do valor de retorno do período de desbloqueio do ranking será alocado de acordo com a proporção do valor do pedido do usuário em cada nível.
- Para os cinco pedidos de Compra 6 a Compra 10, 1⁄50 do valor de retorno do período de desbloqueio será alocado a cada pedido de acordo com a proporção do valor do pedido em cada pedido.
- Para os cinco níveis de ordens de venda de 6 a 10, 1⁄50 do valor de retorno do período de desbloqueio será alocado para cada nível de acordo com a proporção do valor do pedido do usuário em cada nível.
- Para os cinco pedidos da Compra 11 à Compra 15, 1⁄100 do valor de retorno do período de desbloqueio será alocado a cada pedido de acordo com a proporção do valor do pedido em cada pedido.
- Para os cinco pedidos da Venda 11 à Venda 15, 1⁄100 do valor de retorno do período de desbloqueio será alocado a cada pedido de acordo com a proporção do valor do pedido em cada pedido.
O retorno total do desbloqueio da classificação de um usuário em um determinado par de negociação no mesmo dia é a soma do valor devolvido ao usuário pelo desbloqueio da classificação em cada ciclo do par de negociação.
Classificando para desbloquear benefícios
Primeiro, a receita total de triagem e desbloqueio é:
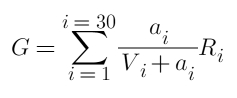
Aqui, i representa uma das posições, há 30 posições no total para ambas as partes, a é a quantidade do pedido pendente, R é o valor do retorno de desbloqueio e V é o número total de pedidos existentes.
Ao contrário do desbloqueio de transações, fazer um pedido não tem custo. Aqui, o R só precisa considerar o tamanho relativo, e não há necessidade de considerar o valor absoluto denominado em USDT. Se determinarmos o número total de ordens pendentes, a questão se torna como alocar as ordens em diferentes posições para maximizar o lucro G. Simplesmente procurar o local com a menor quantidade de pedidos e fazer todos os pedidos lá obviamente não é a solução ideal. Por exemplo, há três posições com 10 ordens existentes, e seu R é o mesmo. Definimos o volume total da ordem para 30. Se escolhermos apenas uma posição para fazer uma ordem, o lucro total final é 0,75R. 10, o o lucro final é de 1,5R, o que mostra que às vezes o lucro de ordens dispersas é melhor. Então, como você aloca fundos?
Otimização de desbloqueio de classificação
Por fim, nossos objetivos e restrições de otimização são:
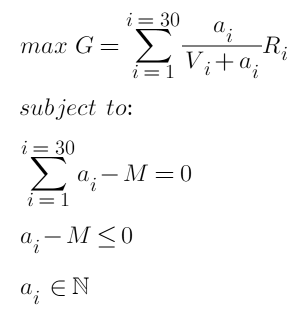
Onde M é a quantidade total do pedido. Este é um problema de otimização convexa quadrática envolvendo desigualdades, que satisfaz a condição KTT e tem uma solução inteira. Usando o pacote correspondente e o solucionador de otimização convexa, deve ser possível obter os resultados diretamente e retornar a quantidade ideal do pedido para cada posição. Mas essa obviamente não é a resposta que queremos. Precisamos simplificar o problema e obter etapas de solução específicas.
Vamos começar com um exemplo simples
Considere apenas dois níveis. Os valores atuais dos pedidos são 10 e 20 (chamados de primeiro nível e segundo nível, respectivamente). Suas cotas de desbloqueio são ambas R. O número total de pedidos de estratégia é 30. Como eles devem ser alocados? Tem a quantidade de fundos desbloqueados foi maximizada? Esta questão parece simples, mas é difícil tirar a conclusão correta sem cálculo. Os leitores podem querer pensar na resposta eles mesmos primeiro.
Cenário 1:
Encontre a posição de ordem mínima e coloque todas as ordens lá, o lucro total G=30/(30+10)=0,75R. Essa também é a solução mais fácil de se pensar.
Cenário 2:
1 yuan é alocado a cada vez e alocado no local que pode gerar o maior lucro, ou seja, o local com o menor número de pedidos pendentes. Então o primeiro yuan será alocado para o primeiro nível, e o volume de pedidos do primeiro nível se tornará 10+1. O segundo yuan também será alocado para o primeiro nível… e assim por diante, até um total de 10 yuan é alocado para o primeiro nível. Neste momento, um será selecionado aleatoriamente e, quando o número total de ordens pendentes no primeiro nível exceder 20, ele será alocado para o segundo nível. O resultado final é que 20 yuans são alocados para o primeiro nível e 10 yuans são alocados para o segundo nível, e seus pedidos finais são ambos 30. Lucro total G=20⁄30+10⁄30=R. Esta solução é muito melhor que a Solução 1 e também é mais fácil de calcular.
Cenário 3:
Podemos assumir que o primeiro nível é alocado a, e o segundo nível é 30-a. Então podemos listar diretamente a equação e encontrar sua derivada como 0 (o processo não está listado aqui, é semelhante ao artigo sobre desbloqueio de transações ), e calcule o resultado final. A fórmula é:
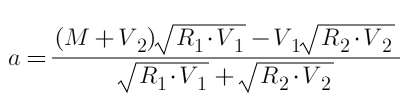
Substitua no inteiro e obtenha a=15. O lucro total G=15⁄25+15⁄35=1,0286R, que é melhor que a Opção 2. Como é diretamente derivado da fórmula, esta é a solução ótima. Os leitores podem conferir.
O resultado pode ser diferente do que você esperava. É óbvio que a alocação de cada dólar no Plano 2 é a solução ótima sob as circunstâncias atuais. Por que não é a solução ótima geral? Essa situação é muito comum. O ótimo local não é necessariamente o ótimo geral, porque antes da alocação, os pedidos já têm fundos investidos, e a eficiência geral precisa considerar os custos irrecuperáveis. Nosso objetivo para cada etapa da otimização é maximizar a eficiência geral em vez de maximizar um único benefício.
Plano de otimização específico
Finalmente, começamos a operação real viável. Vamos simplificar o problema alocando 1 yuan a cada vez. Primeiro, vamos medir a eficiência. A derivada pode refletir a contribuição de cada a para G. Essa contribuição leva em conta o custo cumulativo em vez do benefício de uma única distribuição. Quanto maior o valor, maior a contribuição geral para o benefício final . Obviamente, de acordo com o gráfico da função, quando a=1, a eficiência é maior da existência à não existência, e então diminui gradualmente.
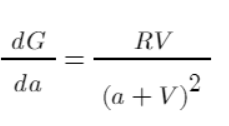
Tomando como exemplo o exemplo simples acima, podemos calcular a eficiência da alocação de fundos e listá-los em uma tabela:
| fundos | 1 | 2 |
|---|---|---|
| 1 | 0.0826 | 0.0454 |
| 2 | 0.069 | 0.0413 |
| 3 | 0.0592 | 0.0378 |
| 4 | 0.051 | 0.0347 |
| 5 | 0.0444 | 0.032 |
| … | … | … |
|12 | 0.0207 |0.0195| |13 | 0.0189 |0.0184| |14 | 0.0174 |0.0173| |15 | 0.016 |0.0163| |16 | 0.0148 |0.0154| |17 | 0.0137 |0.0146| |18 | 0.0128 |0.0139|
De acordo com a tabela, o primeiro yuan é alocado ao primeiro nível, o segundo yuan é alocado ao primeiro nível… o quinto yuan é alocado ao segundo nível… e assim por diante, e finalmente 15 yuan são alocados a o primeiro nível e 15 yuans para o segundo nível. Yuan, que por acaso é a solução ótima que calculamos com base na equação. Especificamente para a 30ª marcha, o algoritmo é o mesmo, e as etapas específicas são:
- 1. Verifique todas as engrenagens primeiro. Se V=0, então a=1, e nenhum outro fundo será alocado.
- 2. Distribua o total de fundos em N partes e selecione uma engrenagem para alocação a cada vez.
- 3. Calcule a eficiência de cada engrenagem = RV/pow(a+V,2), onde a representa os fundos acumulados alocados para a posição + os fundos alocados desta vez.
- 4. Aloque fundos para o equipamento mais eficiente e selecione aleatoriamente um se a eficiência for a mesma.
- 5. Repita 3-4 até que os fundos sejam alocados
Se o volume total do nosso pedido for grande, é muito ineficiente alocar cada dólar de cada vez. Podemos dividir os fundos em 100 partes e alocar uma parte de cada vez. Como é apenas um cálculo e classificação simples, o algoritmo é muito eficiente. Especificamente no nível de execução, ainda há espaço para otimização, como dividir nossos pedidos em 100, para que cada vez que fizermos ajustes, precisemos apenas realocar os pedidos em vez de cancelá-los todos. Você também pode definir o valor R você mesmo e dar mais peso para aqueles que estão longe do mercado. Se houver sobreposições entre o desbloqueio de classificação e o desbloqueio de ordem pendente, você pode considerá-los juntos, e assim por diante.
Este artigo é um artigo original da FMZ Quantitative Platform. Por favor, indique a fonte ao transferir: https://www.fmz.com/bbs-topic-new/5843