Байесовская статистика — мощная дисциплина в математике, имеющая широкое применение во многих областях, включая финансы, медицинские исследования и информационные технологии. Это позволяет нам объединять предыдущие убеждения с доказательствами для получения новых последующих убеждений, что позволяет нам принимать более обоснованные решения.

В этой статье мы кратко представим некоторых выдающихся математиков, основавших эту область.

До Байеса Чтобы лучше понять байесовскую статистику, нам нужно вернуться в XVIII век и обратиться к математику Де Муавуру и его работе «Принцип случая».[1]。

В своем трактате де Муавр затронул многие проблемы своего времени, связанные с вероятностью и азартными играми. Как вы, вероятно, знаете, его решение одной из этих проблем привело к возникновению нормального распределения, но это уже другая история.

В его статье есть простой вопрос:

«Вероятность выпадения трех орлов при подбрасывании честной монеты три раза подряд».

Читая задачи, описанные в «Принципе случайности», вы можете заметить, что большинство из них начинаются с гипотезы, на основе которой рассчитывается вероятность данного события. Например, в приведенной выше задаче предполагается, что монета симметричная, поэтому вероятность выпадения орла при подбрасывании равна 0,5.

Сегодня это выражается математическим языком как:

𝑃(𝑋|𝜃)

Но что, если мы не знаем, честная ли монета? Если мы не знаем𝜃Шерстяная ткань?

Томас Байес и Ричард Прайс

Почти пятьдесят лет спустя, в 1763 году, была опубликована работа под названием «Опыт о решении задач, касающихся принципа случайности».[2] Опубликовано в «Философских трудах» Лондонского королевского общества.

На первых нескольких страницах документа находится текст, написанный математиком Ричардом Прайсом, в котором кратко излагается содержание статьи, написанной его другом Томасом Байесом за несколько лет до его смерти. Во введении Прайс объясняет важность некоторых открытий, сделанных Томасом Байесом, которые не были отражены в «Принципах случайности» Де Муавра.

На самом деле он имел в виду конкретную проблему:

«Зная число появлений и неявок неизвестного события, найдите вероятность его появления между любыми двумя названными степенями вероятности».

Другими словами, после наблюдения за событием мы находим неизвестный параметрθКакова вероятность между двумя степенями вероятности? На самом деле это одна из первых проблем в истории, связанных со статистическим выводом, и именно она дала начало названию «обратная вероятность». В математических терминах:

𝑃( 𝜃 | 𝑋）

Конечно, это то, что сегодня мы называем апостериорным распределением теоремы Байеса.

Необоснованные причины

Познакомьтесь с этими двумя старейшинами-пасторами.Томас БайесиРичард Прайс, то, что побудило меня провести исследование, на самом деле очень интересно. Но чтобы сделать это, нам нужно на время отвлечься от некоторых знаний о статистике.

На дворе XVIII век, и теория вероятностей становится все более интересной для математиков. Такие математики, как Муавр и Бернулли, показали, что некоторые события происходят с определенной степенью случайности, но все же подчиняются фиксированным правилам. Например, если бросить игральную кость много раз, то один раз из шести выпадет шестерка. Как будто существует некое скрытое правило, определяющее судьбу случая.

А теперь представьте, что вы математик и глубоко верующий человек, живущий в наше время. Вам может быть интересно узнать, как это скрытое правило связано с Богом.

Именно этот вопрос задавали себе Байес и Прайс. Решение, с помощью которого они надеялись разрешить эту проблему, было напрямую применимо к доказательству того, что «мир должен быть результатом мудрости и интеллекта; тем самым предоставляя доказательства существования Бога как конечной причины».[2] - То есть, нет причины и следствия.

Лаплас

Удивительно, но примерно два года спустя, в 1774 году, французский математик Лаплас, по-видимому, не прочитав статью Томаса Байеса, написал работу под названием «О причинах событий через вероятности событий».[3], которая представляет собой статью по обратной задаче вероятности. На первой странице вы можете прочитать

Основные принципы:

«Если событие может быть вызвано n различными причинами, то вероятности этих причин для данного события находятся в отношении, равном вероятности события при данной причине, а вероятность существования каждой из этих причин равна к вероятности события при данной причине. Вероятность причин, деленная на сумму вероятностей события при каждой из этих причин».

Это то, что мы сегодня знаем как теорему Байеса:

​

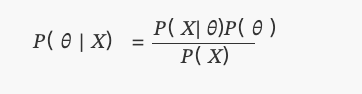
вP(θ)распределено равномерно.

Эксперимент с монетой

Мы применим байесовскую статистику к настоящему времени, используя Python и библиотеку PyMC и проведя простой эксперимент.

Предположим, друг дает вам монету и спрашивает, считаете ли вы ее честной. Поскольку он торопится, он говорит вам подбросить монетку только 10 раз. Как видите, в этой задаче есть неизвестный параметр.p, вероятность выпадения орла при подбрасывании монеты, и мы хотим оценить этоpНаиболее вероятное значение .

(Примечание: мы не говорим о параметрахpявляется случайной величиной, но этот параметр фиксирован, и мы хотим знать, между какими значениями он, скорее всего, будет находиться. ）

Чтобы по-другому взглянуть на эту проблему, рассмотрим ее с точки зрения двух различных априорных убеждений:

• 1. У вас нет предварительной информации о честности монеты и вы назначаете равные вероятностиp. В этом случае мы будем использовать так называемую неинформативную априорную информацию, поскольку вы не добавляете никакой информации к своим убеждениям.
• 1. Вы знаете по опыту, что даже если монета может быть нечестной, ее трудно сделать совсем нечестной, поэтому вы думаете, что параметрыpСкорее всего, он не опустится ниже 0,3 и не превысит 0,7. В этом случае мы будем использовать информативную априорную информацию.

В обоих случаях наши априорные убеждения будут следующими:

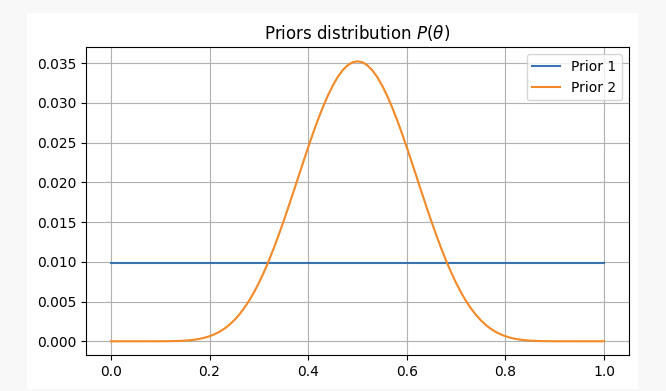
Подбросив монету 10 раз, выпадает 2 орла. Имея эти доказательства, мы, вероятно, сможем понять, где найти наши параметры.p？

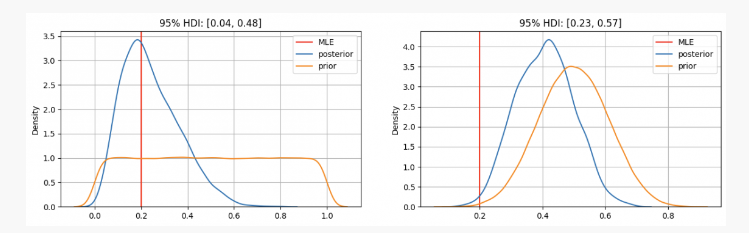
Как видите, в первом случае мы имеемpАприорное распределение центрировано на оценке максимального правдоподобия (MLE)p=0.2, который представляет собой аналогичный подход с использованием частотного метода. Истинный неизвестный параметр будет находиться в 95%-ном доверительном интервале между 0,04 и 0,48.

С другой стороны, когда есть высокая уверенность в том, что параметрp Хотя оно должно быть в пределах от 0,3 до 0,7, мы видим, что апостериорное распределение составляет около 0,4, что намного выше значения, полученного с помощью нашей MLE. В этом случае истинный неизвестный параметр будет лежать в 95% доверительном интервале между 0,23 и 0,57.

Итак, в первом случае вы скажете своему другу, что вы уверены в том, что монета нечестная. Но в другом случае вы бы сказали ему, что не уверены в честности монеты.

Как видите, даже при одинаковых доказательствах (2 орла из 10 подбрасываний) результаты могут быть разными, учитывая разные априорные убеждения. В этом заключается сила байесовской статистики, которая, подобно научному методу, позволяет нам обновлять наши убеждения, объединяя предыдущие убеждения с новыми наблюдениями и доказательствами.

END

В сегодняшней статье мы рассмотрели истоки байесовской статистики и ее основных участников. С тех пор в эту область статистики внесли свой вклад многие другие важные исследователи (Джеффрис, Кокс, Шеннон и т. д.), данные взяты с сайта quantdare.com.