براہ کرم نوٹ کریں: یہ کیس صرف مطالعہ اور تحقیق کے مقاصد کے لئے ہے اور سرمایہ کاری کی سفارش نہیں کرتا ہے۔

بٹ کوائن کی قیمت کا ڈیٹا ٹائم سیریز پر مبنی ہے ، لہذا بٹ کوائن کی قیمت کی پیش گوئی زیادہ تر ایل ایس ٹی ایم ماڈل کے ذریعہ کی جاتی ہے۔

طویل مدتی قلیل مدتی میموری (LSTM) ایک گہری سیکھنے کا ماڈل ہے جو خاص طور پر ٹائم سیریز کے اعداد و شمار (یا اعداد و شمار کے ساتھ وقت / خلائی / ساختہ ترتیب ، جیسے فلم ، جملہ وغیرہ) کے لئے موزوں ہے ، جو کریپٹوکرنسی کی قیمت کی سمت کی پیش گوئی کرنے کا ایک مثالی ماڈل ہے۔

یہ مضمون بنیادی طور پر ایل ایس ٹی ایم کے ذریعے ڈیٹا کی ملاپ کے بارے میں لکھا گیا ہے تاکہ بٹ کوائن کی مستقبل کی قیمت کی پیش گوئی کی جا سکے۔

import کے لئے درکار لائبریری

import pandas as pd
import numpy as np

from sklearn.preprocessing import MinMaxScaler, LabelEncoder
from keras.models import Sequential
from keras.layers import LSTM, Dense, Dropout

from matplotlib import pyplot as plt
%matplotlib inline

ڈیٹا تجزیہ

ڈیٹا لوڈ کریں

بی ٹی سی کی ڈیلی ٹرانزیکشنز پڑھیں۔

data = pd.read_csv(filepath_or_buffer="btc_data_day")

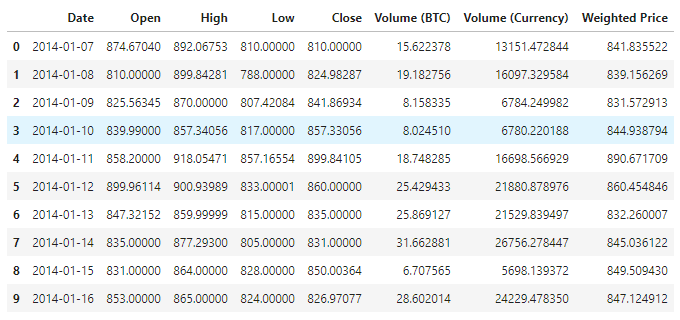
اعداد و شمار کو دیکھنے کے لئے دستیاب ہے ، اب اعداد و شمار کی کل تعداد 1380 ہے ، اعداد و شمار کی تاریخ ، اوپن ، ہائی ، لو ، کلوز ، حجم (بی ٹی سی) ، حجم (کرنسی) ، اور وزن کی قیمت کے کالموں پر مشتمل ہے۔ اس میں تاریخ کالم کو چھوڑ کر ، باقی ڈیٹا کالم فلوٹ 64 ڈیٹا ٹائپ ہیں۔

data.info()

ذیل میں 10 لائنوں کے اعداد و شمار ملاحظہ کریں

data.head(10)

اعداد و شمار کا تصور

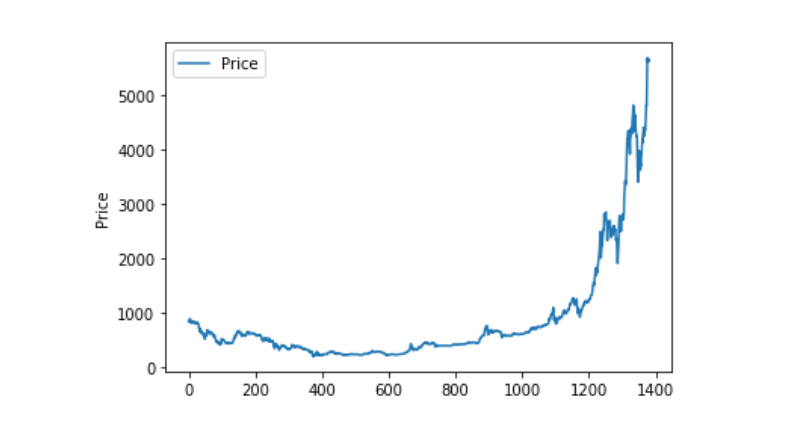
matplotlib کا استعمال کرتے ہوئے وزن کی قیمتوں کا نقشہ بنائیں اور دیکھیں کہ اعداد و شمار کی تقسیم اور اس کی رفتار کیا ہے۔ اعداد و شمار کے ایک حصے میں ہمیں اعداد و شمار کا ایک حصہ ملا ہے ، ہمیں اس بات کی تصدیق کرنے کی ضرورت ہے کہ آیا اعداد و شمار میں کوئی غیر معمولی بات ہے یا نہیں۔

plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()

غیر معمولی ڈیٹا پروسیسنگ

ہم نے پہلے دیکھا کہ آیا اعداد و شمار میں نان اعداد و شمار موجود ہیں، اور ہم نے دیکھا کہ ہمارے اعداد و شمار میں نان اعداد و شمار موجود نہیں ہیں۔

data.isnull().sum()

Date                 0
Open                 0
High                 0
Low                  0
Close                0
Volume (BTC)         0
Volume (Currency)    0
Weighted Price       0
dtype: int64

اور اب ہم اعداد و شمار 0 پر نظر ڈالتے ہیں، اور آپ دیکھ سکتے ہیں کہ ہمارے اعداد و شمار میں 0 کی قدر ہے، اور ہمیں 0 کی قدر کے ساتھ کام کرنے کی ضرورت ہے.

(data == 0).astype(int).any()

Date                 False
Open                  True
High                  True
Low                   True
Close                 True
Volume (BTC)          True
Volume (Currency)     True
Weighted Price        True
dtype: bool

data['Weighted Price'].replace(0, np.nan, inplace=True)
data['Weighted Price'].fillna(method='ffill', inplace=True)
data['Open'].replace(0, np.nan, inplace=True)
data['Open'].fillna(method='ffill', inplace=True)
data['High'].replace(0, np.nan, inplace=True)
data['High'].fillna(method='ffill', inplace=True)
data['Low'].replace(0, np.nan, inplace=True)
data['Low'].fillna(method='ffill', inplace=True)
data['Close'].replace(0, np.nan, inplace=True)
data['Close'].fillna(method='ffill', inplace=True)
data['Volume (BTC)'].replace(0, np.nan, inplace=True)
data['Volume (BTC)'].fillna(method='ffill', inplace=True)
data['Volume (Currency)'].replace(0, np.nan, inplace=True)
data['Volume (Currency)'].fillna(method='ffill', inplace=True)

(data == 0).astype(int).any()

Date                 False
Open                 False
High                 False
Low                  False
Close                False
Volume (BTC)         False
Volume (Currency)    False
Weighted Price       False
dtype: bool

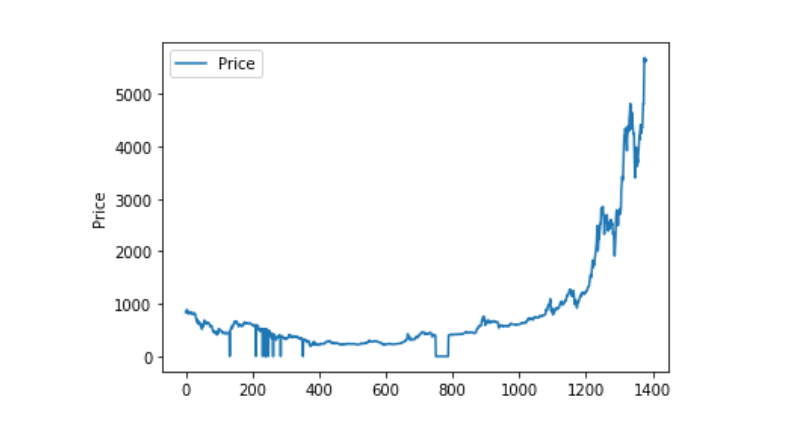
اور اب ہم اس کی تقسیم اور اس کی رفتار پر نظر ڈالتے ہیں، اور اس وقت یہ بہت مسلسل ہے.

plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()

ٹریننگ ڈیٹا سیٹ اور ٹیسٹنگ ڈیٹا سیٹ کی تقسیم

اعداد و شمار کو 0-1 میں یکساں کریں

data_set = data.drop('Date', axis=1).values
data_set = data_set.astype('float32')
mms = MinMaxScaler(feature_range=(0, 1))
data_set = mms.fit_transform(data_set)

ٹیسٹ ڈیٹا سیٹ اور ٹریننگ ڈیٹا سیٹ کو 2:8 سے تقسیم کریں

ratio = 0.8
train_size = int(len(data_set) * ratio)
test_size = len(data_set) - train_size
train, test = data_set[0:train_size,:], data_set[train_size:len(data_set),:]

ٹریننگ ڈیٹا سیٹ اور ٹیسٹنگ ڈیٹا سیٹ بنائیں۔ ہمارے ٹریننگ ڈیٹا سیٹ اور ٹیسٹنگ ڈیٹا سیٹ کو ونڈو مدت کے طور پر ایک دن میں بنائیں۔

def create_dataset(data):
    window = 1
    label_index = 6
    x, y = [], []
    for i in range(len(data) - window):
        x.append(data[i:(i + window), :])
        y.append(data[i + window, label_index])
    return np.array(x), np.array(y)

train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)

ماڈل کی وضاحت اور تربیت

اس بار ہم نے ایک سادہ ماڈل استعمال کیا ہے، جس کی ساخت یہ ہے:. LSTM2. Dense。

یہاں ایل ایس ٹی ایم کے ان پٹ شیپ کے بارے میں وضاحت کی ضرورت ہے ، ان پٹ شیپ کی ان پٹ طول و عرض ((batch_size, time steps, features)) ہے۔ اس میں ، ٹائم اسٹیپس کی قدر ڈیٹا ان پٹ کے وقت کی ٹائم ونڈو کا وقفہ ہے۔ یہاں ہم 1 دن کو ٹائم ونڈو کے طور پر استعمال کرتے ہیں ، اور ہمارے ڈیٹا دن کے اعداد و شمار ہیں ، لہذا یہاں ہمارے ٹائم اسٹیپس 1 ہیں۔

لمبی مختصر مدت کی یادداشت (LSTM) ایک خاص قسم کی RNN ہے جو بنیادی طور پر لمبی ترتیب کی تربیت کے دوران تدریجی غائب اور تدریجی دھماکے کے مسائل کو حل کرنے کے لئے ہے۔ یہاں LSTM کا مختصر تعارف ہے۔

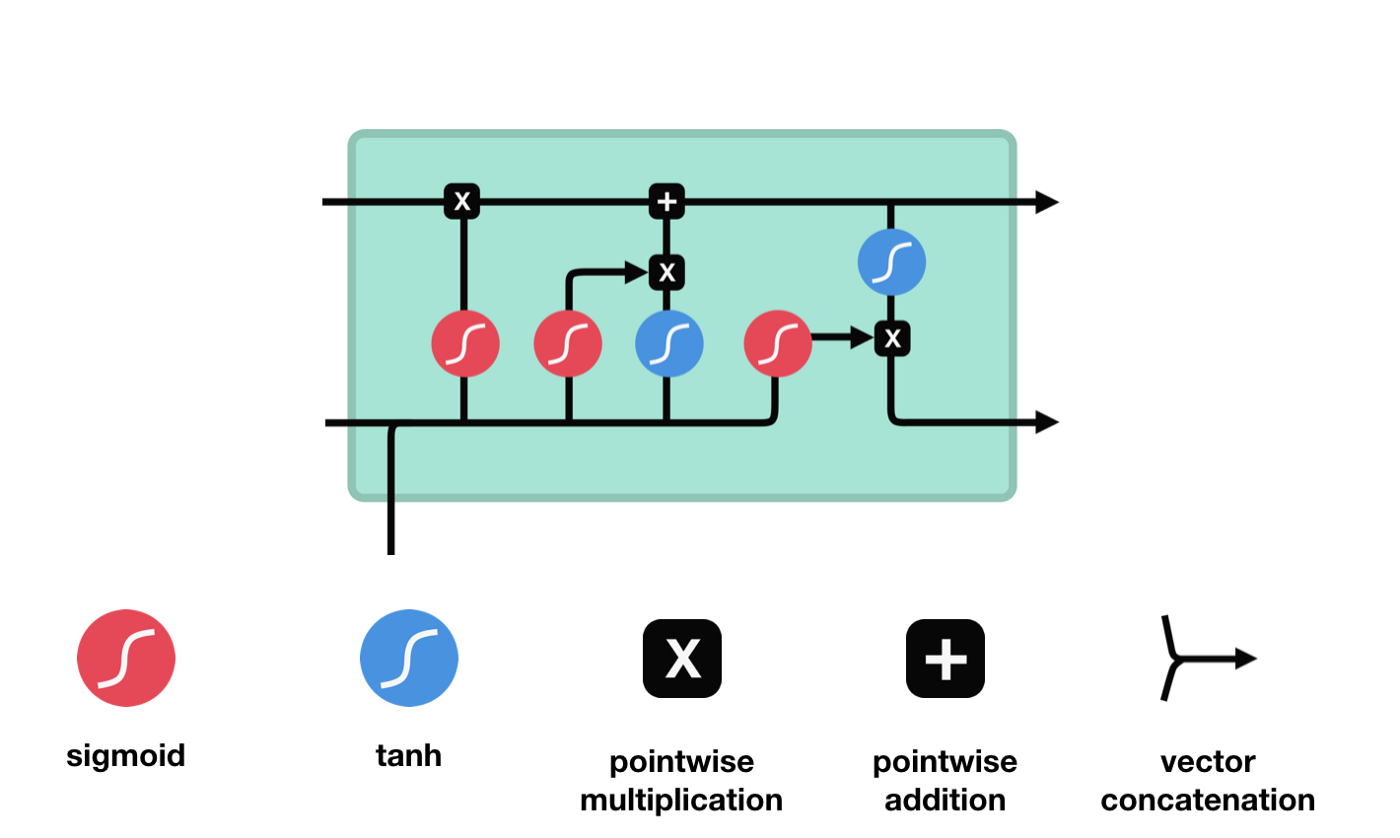
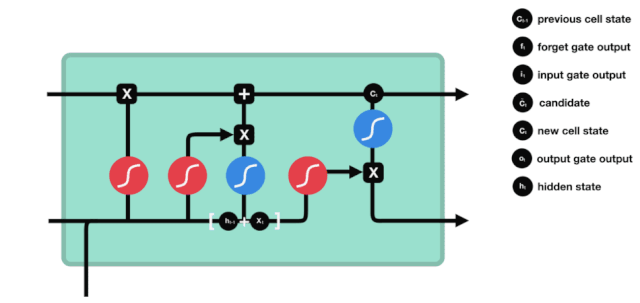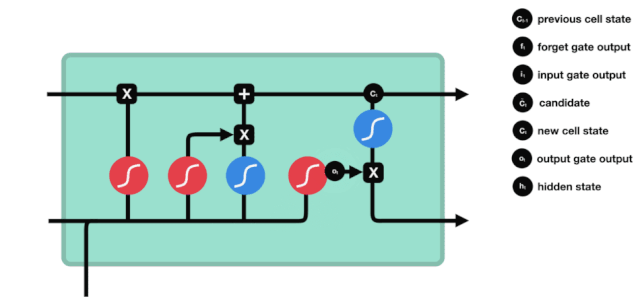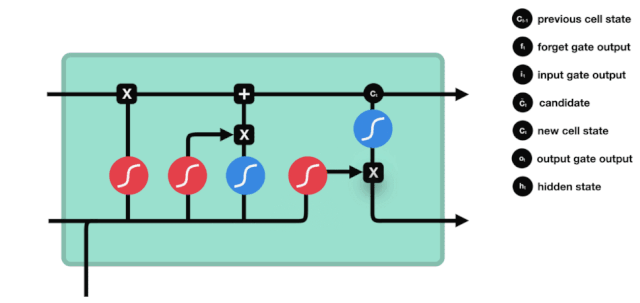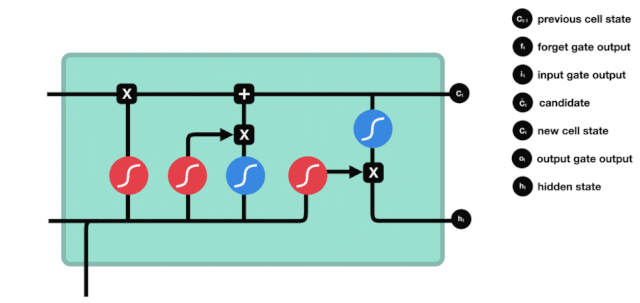
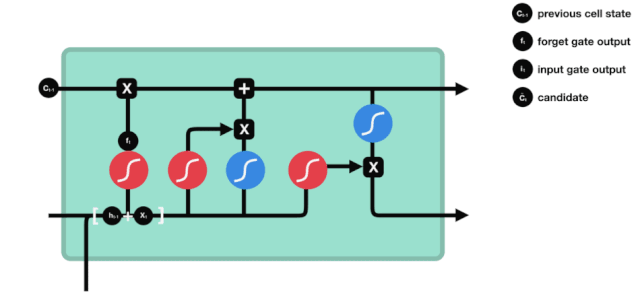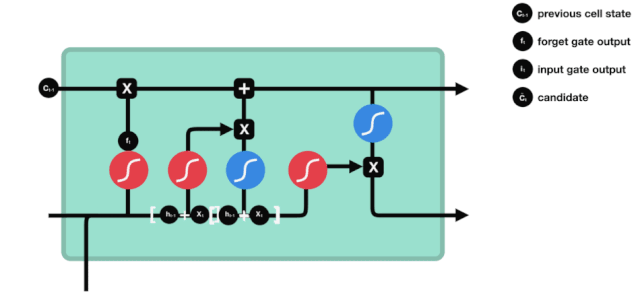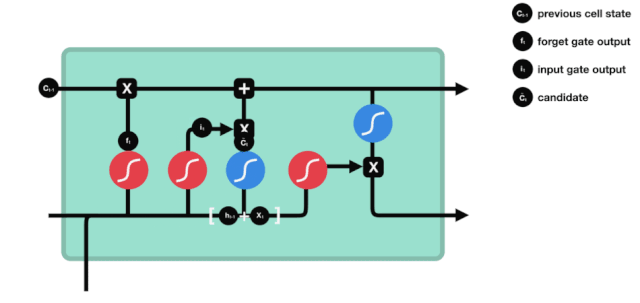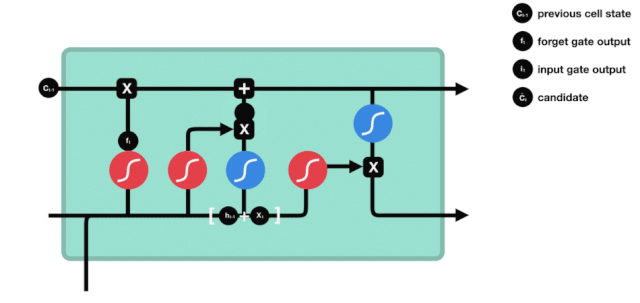
ایل ایس ٹی ایم کے نیٹ ورک ڈھانچے کے نقشے سے ، یہ دیکھا جاسکتا ہے کہ ایل ایس ٹی ایم دراصل ایک چھوٹا سا ماڈل ہے جس میں 3 سگمائڈ ایکٹیویشن فنکشن ، 2 تانہ ایکٹیویشن فنکشن ، 3 ضرب اور 1 جمع شامل ہیں۔

سیل کی حالت

سیل کی حالت ایل ایس ٹی ایم کا مرکز ہے ، وہ اوپر کی تصویر میں سب سے اوپر کی سیاہ لائن ہے ، اس سیاہ لائن کے نیچے کچھ دروازے ہیں ، جن کے بارے میں ہم بعد میں بات کریں گے۔ سیل کی حالت ہر دروازے کے نتائج کے مطابق اپ ڈیٹ کی جائے گی۔ ذیل میں ہم ان دروازوں کے بارے میں بات کرتے ہیں ، لہذا آپ سیل کی حالت کے عمل کو سمجھیں گے۔

ایل ایس ٹی ایم نیٹ ورک سیل کی حیثیت سے معلومات کو حذف یا شامل کرنے کے لئے ایک ڈھانچے کے ذریعہ استعمال کیا جاتا ہے جسے گیٹ کہا جاتا ہے۔ گیٹ منتخب فیصلے کرنے کے قابل ہے کہ کون سے معلومات کو گزرنے دیں۔ گیٹ کی ساخت ایک سگمائڈ پرت اور ایک نقطہ ضرب آپریشن کا ایک مجموعہ ہے۔ چونکہ سگمائڈ پرت کی پیداوار 0 سے 1 کی قدر ہے ، لہذا 0 کا مطلب یہ نہیں ہے کہ کوئی بھی گزر نہیں سکتا ، 1 کا مطلب یہ ہے کہ کوئی بھی گزر سکتا ہے۔ ایک ایل ایس ٹی ایم میں تین دروازے شامل ہیں جو سیل کی حیثیت کو کنٹرول کرتے ہیں۔ ذیل میں ہم ان دروازوں میں سے ایک کے بارے میں بات کریں گے۔

بھول جانے کا دروازہ

ایل ایس ٹی ایم کا پہلا قدم یہ طے کرنا ہے کہ کون سی معلومات کو سیلولر ریاست کو ضائع کرنے کی ضرورت ہے۔ اس حصے کا آپریشن ایک سگمائڈ یونٹ کے ذریعے کیا جاتا ہے جسے بھولنے کا دروازہ کہا جاتا ہے۔ آئیے متحرک اشارے پر ایک نظر ڈالیں ، جس میں یہ بتایا گیا ہے کہ اس طرح کی معلومات کو ضائع کرنے کے لئے سیلولر ریاست کو کیا کرنا چاہئے۔

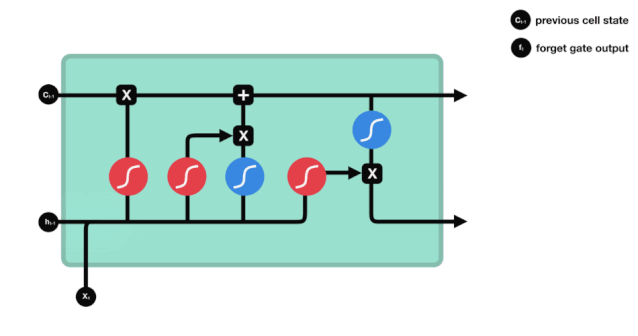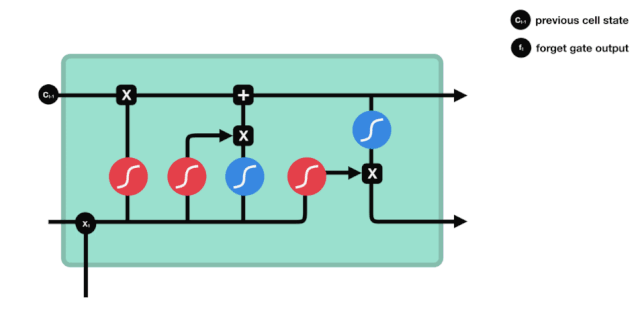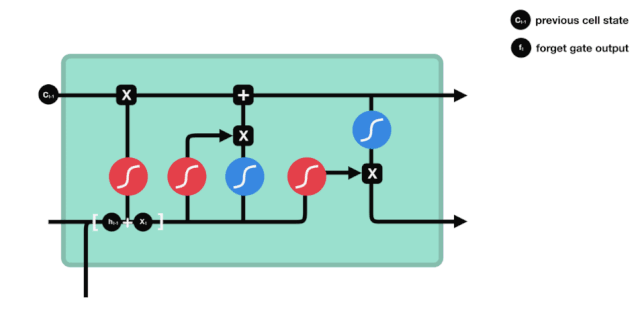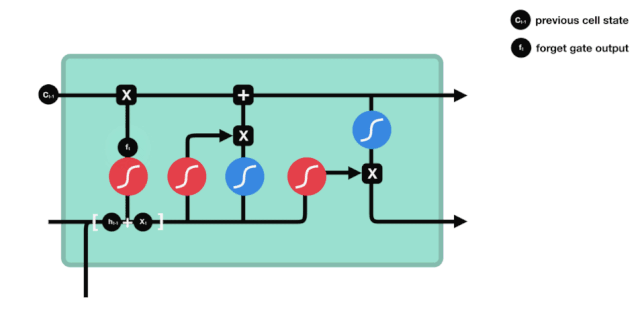
ہم دیکھ سکتے ہیں کہ بھول جانے والا دروازہ \( h_ {l-1} \) اور \( x_ {t} \) معلومات کو دیکھ کر 0-1 کے درمیان ایک ویکٹر کو آؤٹ پٹ کرتا ہے۔ اس ویکٹر کے اندر 0-1 کی قدر یہ بتاتی ہے کہ سیل کی حالت \( C_ {t-1} \) میں سے کون سی معلومات کو برقرار رکھا یا ضائع کیا گیا ہے۔ 0 کو برقرار نہیں رکھا گیا اور 1 کو برقرار رکھا گیا۔

ریاضیاتی اظہار: \(f_{t} =\sigma\left(W_{f} \cdot\left[h_{t-1}, x_{t}\right]+b_{f}\right)\)

ان پٹ

اگلا قدم یہ فیصلہ کرنا ہے کہ کون سی نئی معلومات سیل کی حالت میں شامل کی جائیں۔ یہ قدم ان پٹ کے ذریعے کیا جاتا ہے۔ آئیے پہلے متحرک اشارے پر نظر ڈالتے ہیں، جس سے پتہ چلتا ہے کہ سیل کی حالت میں کون سی نئی معلومات شامل کی جائیں گی۔

ہم دیکھتے ہیں کہ \(h_{l-1}\) اور \(x_{t}\) کا پیغام ایک بھول گیٹ (sigmoid) اور ان پٹ (tanh) میں ڈال دیا گیا ہے۔ چونکہ بھول گیٹ کی آؤٹ پٹ 0 سے 1 کی قدر ہے ، لہذا اگر بھول گیٹ کی آؤٹ پٹ 0 ہے تو ، ان پٹ کے بعد کا نتیجہ \( C_{i}\) موجودہ سیل ریاست میں شامل نہیں کیا جائے گا۔ اگر یہ 1 ہے تو ، یہ سب سیل ریاست میں شامل کیا جائے گا ، لہذا یہاں بھول گیٹ کا کام ان پٹ کے نتائج کو سیل ریاست میں منتخب طور پر شامل کرنا ہے۔

ریاضی کی فارمولہ ہے: \(C_{t}=f_{t} * C_{t-1}+i_{t} *\tilde{C}_{t}\)

باہر نکلنے کے دروازے

سیل کی حالت کو اپ ڈیٹ کرنے کے بعد یہ طے کرنے کی ضرورت ہے کہ آؤٹ پٹ سیل کی کون سی حالت کی خصوصیات \( h_ {l-1} \) اور \( x_ {t} \) ان پٹ کے مجموعے کے مطابق ہیں۔ یہاں ان پٹ کو آؤٹ پٹ گیٹ نامی سگمائڈ پرت سے طے کرنے کی ضرورت ہے ، اور پھر سیل کی حالت کو تانھ پرت سے طے کرنے کی ضرورت ہے جس کی قیمت -1 ~ 1 کے درمیان ہے۔ اس ویکٹر کو آؤٹ پٹ گیٹ سے طے شدہ شرائط کے ساتھ مل کر اس آخری RNN یونٹ کی پیداوار مل جاتی ہے۔

def create_model():
    model = Sequential()
    model.add(LSTM(50, input_shape=(train_x.shape[1], train_x.shape[2])))
    model.add(Dense(1))
    model.compile(loss='mae', optimizer='adam')
    model.summary()
    return model

model = create_model()

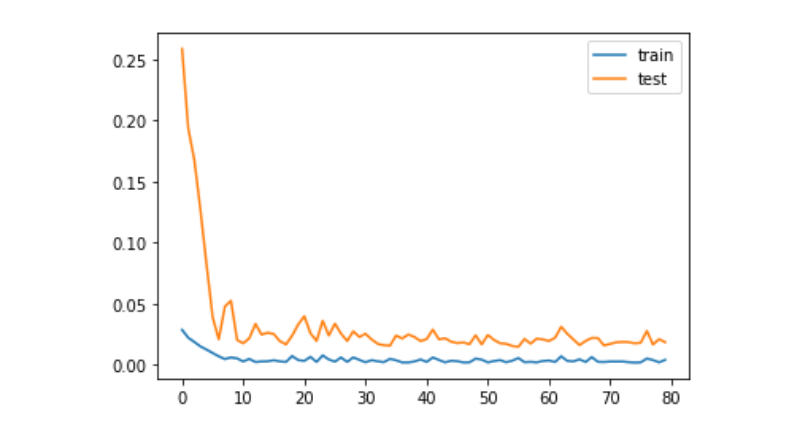
history = model.fit(train_x, train_y, epochs=80, batch_size=64, validation_data=(test_x, test_y), verbose=1, shuffle=False)

plt.plot(history.history['loss'], label='train')
plt.plot(history.history['val_loss'], label='test')
plt.legend()
plt.show()

train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)

پیش گوئی

predict = model.predict(test_x)
plt.plot(predict, label='predict')
plt.plot(test_y, label='ground true')
plt.legend()
plt.show()

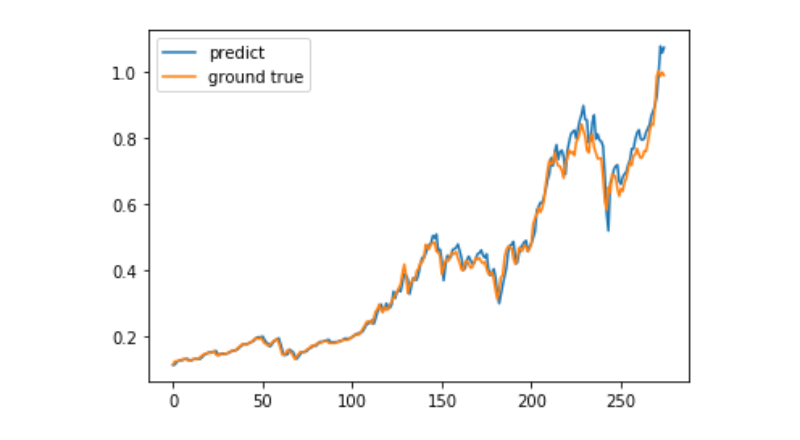
مشین لرننگ کا استعمال کرتے ہوئے بٹ کوائن کی طویل مدتی قیمتوں کی پیش گوئی کرنا ابھی بھی بہت مشکل ہے۔ یہ مضمون صرف ایک سیکھنے کے معاملے کے طور پر استعمال کیا جاسکتا ہے۔ اس معاملے کے بعد میٹرک پول کلاؤڈ کے ساتھ ڈیمو شبیہیں آن لائن ہوں گی ، اور دلچسپی رکھنے والے صارفین براہ راست تجربہ کرسکتے ہیں۔