1. مختصر تعارف

گہرے عصبی نیٹ ورک حالیہ برسوں میں تیزی سے مقبول ہوئے ہیں، بہت سے شعبوں میں پہلے ناقابل حل مسائل کو حل کرتے ہیں اور اپنی طاقتور صلاحیتوں کا مظاہرہ کرتے ہیں۔ ٹائم سیریز کی پیشن گوئی میں، عام طور پر استعمال ہونے والی نیورل نیٹ ورک کی قیمت RNN ہے، کیونکہ RNN میں نہ صرف موجودہ ڈیٹا ان پٹ ہوتا ہے، بلکہ تاریخی ڈیٹا ان پٹ بھی ہوتا ہے، جب ہم RNN کی پیشن گوئی کی قیمتوں کے بارے میں بات کرتے ہیں، تو ہم اکثر RNN کی ایک قسم کے بارے میں بات کرتے ہیں۔ : LSTM یہ مضمون pytorch کی بنیاد پر Bitcoin کی قیمتوں کی پیشن گوئی کرنے کے لیے ایک ماڈل بنائے گا۔ اگرچہ انٹرنیٹ پر بہت ساری متعلقہ معلومات موجود ہیں، اور ابھی بھی نسبتاً کم لوگ ہیں جو pytorch کا استعمال کرتے ہیں، حتمی نتیجہ یہ ہے کہ ابتدائی قیمت، اختتامی قیمت کا استعمال کیا جائے۔ اگلی اختتامی قیمت کا اندازہ لگانے کے لیے بٹ کوائن مارکیٹ کی سب سے زیادہ قیمت، سب سے کم قیمت اور لین دین کا حجم۔ نیورل نیٹ ورکس کے بارے میں میرا ذاتی علم اوسط ہے، اور میں آپ کی تنقید اور اصلاح کا خیر مقدم کرتا ہوں۔ یہ ٹیوٹوریل FMZ کی طرف سے تیار کیا گیا ہے، جو کہ ڈیجیٹل کرنسی کوانٹیٹیو ٹریڈنگ پلیٹ فارم (www.fmz.com) کے موجد ہے QQ گروپ: 863946592 میں کمیونیکیشن کے لیے خوش آمدید۔

2. ڈیٹا اور حوالہ جات

متعلقہ قیمت کی پیشین گوئی کی مثال: https://yq.aliyun.com/articles/538484 RNN ماڈل کا تفصیلی تعارف: https://zhuanlan.zhihu.com/p/27485750 RNN کے ان پٹ اور آؤٹ پٹ کو سمجھنا: https://www.zhihu.com/question/41949741/answer/318771336 pytorch کے بارے میں: سرکاری دستاویزات https://pytorch.org/docs دیگر معلومات خود تلاش کریں۔ اس کے علاوہ، اس مضمون کو سمجھنے کے لیے کچھ لازمی معلومات کی ضرورت ہے، جیسے پانڈاس/کرالرز/ڈیٹا پروسیسنگ وغیرہ، لیکن اگر آپ اسے نہیں جانتے ہیں تو اس سے کوئی فرق نہیں پڑتا۔

3. pytorch LSTM ماڈل کے پیرامیٹرز

LSTM کے پیرامیٹرز:

جب میں نے پہلی بار دستاویز پر ان گنجان بھرے پیرامیٹرز کو دیکھا تو میرا ردعمل یہ تھا: جیسا کہ میں نے آہستہ آہستہ پڑھا، میں نے آخر میں اسے سمجھا.

input_size: ان پٹ ویکٹر x کا فیچر سائز اگر بند ہونے والی قیمت کا اندازہ لگانے کے لیے استعمال کیا جاتا ہے، تو input_size=1؛ اگر اختتامی قیمت کی پیش گوئی زیادہ ہو اور کم ہو، تو input_size=4 hidden_size: پوشیدہ پرت کا سائز num_layers: RNN کی تہوں کی تعداد batch_first: اگر درست ہے تو، پہلا ان پٹ ڈائمینشن ہے batch_size یہ پیرامیٹر بھی بہت مبہم ہے اور ذیل میں تفصیل سے بیان کیا جائے گا۔

ان پٹ ڈیٹا پیرامیٹرز:

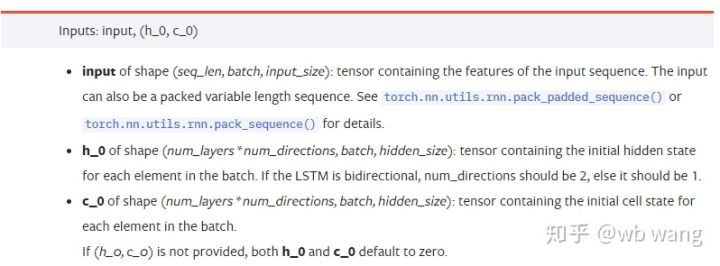
input: مخصوص ان پٹ ڈیٹا ایک تین جہتی ٹینسر ہے جس کی مخصوص شکل (seq_len، بیچ، input_size) ہے۔ ان میں سے، seq_len سے مراد ترتیب کی لمبائی ہے، یعنی تاریخی ڈیٹا LSTM کو کتنی دیر تک غور کرنے کی ضرورت ہے۔ مختلف seq_len کے ساتھ ان پٹ ڈیٹا اور بیچ کے سائز سے مراد ہے، جو کہ پچھلے input_size کے کتنے مختلف گروپس ہیں؛ h_0: ابتدائی پوشیدہ حالت، شکل ہے (num_layers * num_directions، بیچ، hidden_size)، اگر یہ ایک دو طرفہ نیٹ ورک ہے num_directions=2 c_0: سیل کی ابتدائی حالت، شکل اوپر کی طرح ہی ہے، غیر متعینہ چھوڑا جا سکتا ہے۔

آؤٹ پٹ پیرامیٹرز:

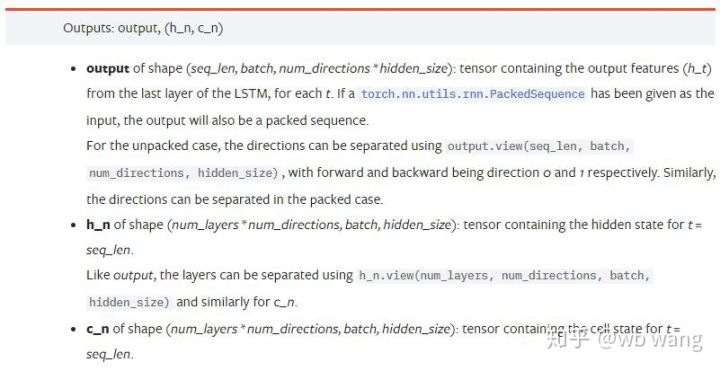
output: آؤٹ پٹ شکل (seq_len، بیچ، num_directions * hidden_size)، نوٹ کریں کہ اس کا تعلق ماڈل پیرامیٹر batch_first سے ہے h_n: h وقت پر حالت t = seq_len، وہی شکل جو h_0 ہے۔ c_n: c وقت پر حالت t = seq_len، c_0 جیسی شکل

4. LSTM ان پٹ اور آؤٹ پٹ کی سادہ مثال

پہلے مطلوبہ پیکجز درآمد کریں۔

import pandas as pd
import numpy as np
import torch
import torch.nn as nn
import matplotlib.pyplot as plt

LSTM ماڈل کی وضاحت

LSTM = nn.LSTM(input_size=5, hidden_size=10, num_layers=2, batch_first=True)

ان پٹ ڈیٹا کی تیاری

x = torch.randn(3,4,5)
# x的值为:
tensor([[[ 0.4657,  1.4398, -0.3479,  0.2685,  1.6903],
         [ 1.0738,  0.6283, -1.3682, -0.1002, -1.7200],
         [ 0.2836,  0.3013, -0.3373, -0.3271,  0.0375],
         [-0.8852,  1.8098, -1.7099, -0.5992, -0.1143]],

        [[ 0.6970,  0.6124, -0.1679,  0.8537, -0.1116],
         [ 0.1997, -0.1041, -0.4871,  0.8724,  1.2750],
         [ 1.9647, -0.3489,  0.7340,  1.3713,  0.3762],
         [ 0.4603, -1.6203, -0.6294, -0.1459, -0.0317]],

        [[-0.5309,  0.1540, -0.4613, -0.6425, -0.1957],
         [-1.9796, -0.1186, -0.2930, -0.2619, -0.4039],
         [-0.4453,  0.1987, -1.0775,  1.3212,  1.3577],
         [-0.5488,  0.6669, -0.2151,  0.9337, -1.1805]]])

x کی شکل (3,4,5) ہے، چونکہ ہم نے وضاحت کی ہے۔batch_first=Trueاس وقت، بیچ_سائز 3 ہے، sqe_len 4 ہے، اور input_size 5 ہے۔ x[0] پہلے بیچ کی نمائندگی کرتا ہے۔

اگر batch_first کی تعریف نہیں کی گئی ہے، تو یہ False پر ڈیفالٹ ہو جاتا ہے، اور ڈیٹا کو مکمل طور پر مختلف انداز میں پیش کیا جاتا ہے، جس کا بیچ سائز 4، sqe_len کا 3، اور input_size 5 ہوتا ہے۔ اس وقت ایکس[0] t=0 پر تمام بیچوں کے ڈیٹا کی نمائندگی کرتا ہے، وغیرہ۔ میں ذاتی طور پر محسوس کرتا ہوں کہ یہ ترتیب بدیہی نہیں ہے، اس لیے میں نے پیرامیٹر شامل کیا۔batch_first=True.

دونوں کے درمیان ڈیٹا کی تبدیلی بھی بہت آسان ہے:x.permute(1,0,2)

ان پٹ اور آؤٹ پٹ

ایل ایس ٹی ایم ان پٹ اور آؤٹ پٹ کی شکل کو الجھن میں ڈالنا آسان ہے، سمجھنے میں مدد کے لیے درج ذیل اعداد و شمار کی مدد سے:
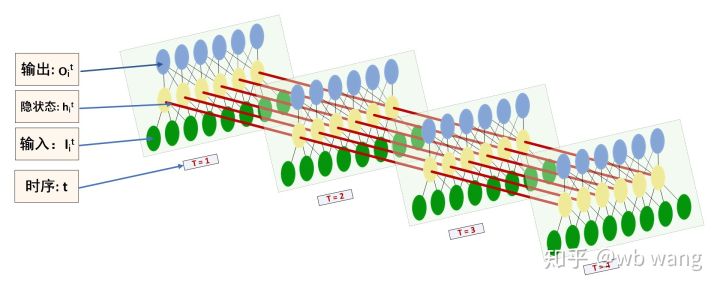
ماخذ: https://www.zhihu.com/question/41949741/answer/318771336

x = torch.randn(3,4,5)
h0 = torch.randn(2, 3, 10)
c0 = torch.randn(2, 3, 10)
output, (hn, cn) = LSTM(x, (h0, c0))
print(output.size()) #在这里思考一下,如果batch_first=False输出的大小会是多少?
print(hn.size())
print(cn.size())
#结果
torch.Size([3, 4, 10])
torch.Size([2, 3, 10])
torch.Size([2, 3, 10])

آؤٹ پٹ کے نتائج کا مشاہدہ کریں، جو پچھلے پیرامیٹر کی وضاحت سے مطابقت رکھتے ہیں۔ نوٹ کریں کہ hn.size() کی دوسری قدر 3 ہے، جو batch_size کے سائز سے مطابقت رکھتی ہے، جس سے ظاہر ہوتا ہے کہ hn میں کوئی درمیانی حالت محفوظ نہیں ہے، صرف آخری مرحلہ ہے۔ چونکہ ہمارے LSTM نیٹ ورک کی دو پرتیں ہیں، اس لیے hn کی آخری پرت کا آؤٹ پٹ دراصل آؤٹ پٹ کی قدر ہے، اور آؤٹ پٹ کی شکل[3، 4، 10]، تمام لمحات کے نتائج کو محفوظ کرتا ہے t=0,1,2,3، اس طرح:

hn[-1][0] == output[0][-1] #第一个batch在hn最后一层的输出等于第一个batch在t=3时output的结果
hn[-1][1] == output[1][-1]
hn[-1][2] == output[2][-1]

5. بٹ کوائن مارکیٹ ڈیٹا تیار کریں۔

میں نے پہلے جو کچھ کہا ہے وہ صرف ایک پیش کش ہے LSTM کے ان پٹ اور آؤٹ پٹ کو سمجھنا بہت ضروری ہے ورنہ اگر آپ انٹرنیٹ سے تصادفی طور پر کچھ کوڈز کاپی کرتے ہیں۔ وقت کی سیریز میں LSTM، چاہے ماڈل غلط ہو، آپ اسے آخر میں حاصل کر سکتے ہیں۔

ڈیٹا کا حصول

استعمال شدہ ڈیٹا BTC_USD Bitfinex ایکسچینج کے تجارتی جوڑے کا مارکیٹ ڈیٹا ہے۔

import requests
import json

resp = requests.get('https://q.fmz.com/chart/history?symbol=bitfinex.btc_usd&resolution=15&from=0&to=0&from=1525622626&to=1562658565')
data = resp.json()
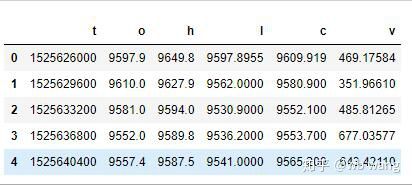
df = pd.DataFrame(data,columns = ['t','o','h','l','c','v'])
print(df.head(5))

ڈیٹا فارمیٹ مندرجہ ذیل ہے:

ڈیٹا پری پروسیسنگ

df.index = df['t'] # index设为时间戳
df = (df-df.mean())/df.std() # 数据的标准化,否则模型的Loss会非常大,不利于收敛
df['n'] = df['c'].shift(-1) # n为下一个周期的收盘价,是我们预测的目标
df = df.dropna()
df = df.astype(np.float32) # 改变下数据格式适应pytorch

ڈیٹا کی معیاری کاری کا طریقہ بہت مشکل ہے اور یہ صرف نمائش کے لیے ہے جیسے کہ پیداوار۔

تربیتی ڈیٹا کی تیاری

seq_len = 10 # 输入10个周期的数据
train_size = 800 # 训练集batch_size
def create_dataset(data, seq_len):
    dataX, dataY=[], []
    for i in range(0,len(data)-seq_len, seq_len):
        dataX.append(data[['o','h','l','c','v']][i:i+seq_len].values)
        dataY.append(data['n'][i:i+seq_len].values)
    return np.array(dataX), np.array(dataY)
data_X, data_Y = create_dataset(df, seq_len)
train_x = torch.from_numpy(data_X[:train_size].reshape(-1,seq_len,5)) #变化形状,-1代表的值会自动计算
train_y = torch.from_numpy(data_Y[:train_size].reshape(-1,seq_len,1))

train_x اور train_y کی آخری شکلیں ہیں: torch.Size([800, 10, 5]), torch.Size([800، 10، 1])۔ چونکہ ہمارا ماڈل 10 ادوار کے اعداد و شمار کی بنیاد پر اگلی مدت کی اختتامی قیمت کی پیشین گوئی کرتا ہے، اس لیے نظریاتی طور پر، 800 بیچوں کے لیے صرف 800 پیش گوئی شدہ اختتامی قیمتوں کی ضرورت ہوتی ہے۔ لیکن ٹرین_y کے پاس ہر بیچ میں 10 ڈیٹا ہوتا ہے، درحقیقت ہر بیچ کی پیشن گوئی کے درمیانی نتائج کو برقرار رکھا جاتا ہے، نہ صرف آخری۔ حتمی نقصان کا حساب لگاتے وقت، تمام 10 پیشین گوئی کے نتائج کو مدنظر رکھا جا سکتا ہے اور ٹرین_y میں اصل قدروں سے موازنہ کیا جا سکتا ہے۔ نظریاتی طور پر، صرف آخری پیشین گوئی کے نتیجے کے نقصان کا حساب لگانا بھی ممکن ہے۔ میں نے اس مسئلے کو واضح کرنے کے لیے ایک کھردرا خاکہ کھینچا۔ چونکہ LSTM ماڈل میں اصل میں seq_len پیرامیٹر نہیں ہوتا ہے، اس لیے ماڈل کو مختلف لمبائیوں پر لاگو کیا جا سکتا ہے، اور درمیانی پیشین گوئی کے نتائج بھی معنی خیز ہیں، اس لیے میں نقصان کے حساب کو ضم کرنے کا رجحان رکھتا ہوں۔

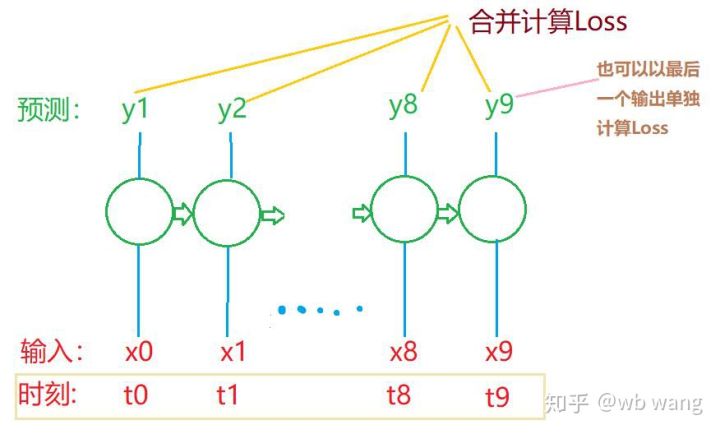
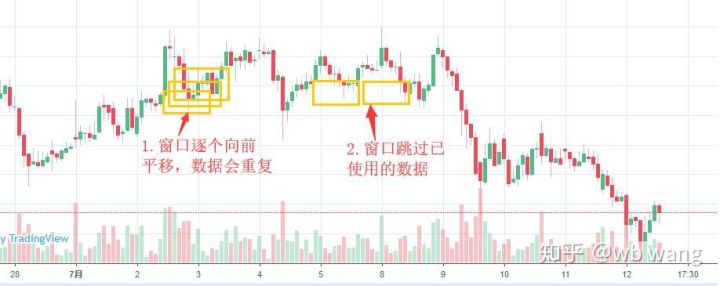
یاد رکھیں کہ تربیتی ڈیٹا تیار کرتے وقت، ونڈو کی نقل و حرکت تیز ہوتی ہے، اور جو ڈیٹا استعمال کیا جا چکا ہے، یقیناً، ونڈوز کو بھی ایک ایک کر کے منتقل کیا جا سکتا ہے، تاکہ حاصل کردہ تربیت کا سیٹ بہت بڑا ہو۔ . لیکن میں نے محسوس کیا کہ ملحقہ بیچ کا ڈیٹا بہت دہرایا گیا تھا، اس لیے میں نے موجودہ طریقہ اپنایا۔

6. LSTM ماڈل کی تعمیر

حتمی ماڈل مندرجہ ذیل ہے، جس میں دو پرت LSTM اور ایک لکیری تہہ شامل ہے۔

class LSTM(nn.Module):
    def __init__(self, input_size, hidden_size, output_size=1, num_layers=2):
        super(LSTM, self).__init__()
        self.rnn = nn.LSTM(input_size,hidden_size,num_layers,batch_first=True)
        self.reg = nn.Linear(hidden_size,output_size) # 线性层,把LSTM的结果输出成一个值

    def forward(self, x):
        x, _ = self.rnn(x) # 如果不理解前向传播中数据维度的变化,可单独调试
        x = self.reg(x)
        return x
        
net = LSTM(5, 10) # input_size为5,代表了高开低收和交易量. 隐含层为10.

7. ماڈل کی تربیت شروع کریں۔

آخر کار تربیت شروع ہوئی، کوڈ درج ذیل ہے:

criterion = nn.MSELoss() # 使用了简单的均方差损失函数
optimizer = torch.optim.Adam(net.parameters(),lr=0.01) # 优化函数,lr可调
for epoch in range(600): # 由于速度很快,这里的epoch多一些
    out = net(train_x) # 由于数据量很小, 直接拿全量数据计算
    loss = criterion(out, train_y)
    optimizer.zero_grad()
    loss.backward() # 反向传播损失
    optimizer.step() # 更新参数
    print('Epoch: {:<3}, Loss:{:.6f}'.format(epoch+1, loss.item()))

تربیت کے نتائج درج ذیل ہیں:

8. ماڈل کی تشخیص

ماڈل کی پیشن گوئی کی قدریں ہیں:

p = net(torch.from_numpy(data_X))[:,-1,0] # 这里只取最后一个预测值作为比较
plt.figure(figsize=(12,8))
plt.plot(p.data.numpy(), label= 'predict')
plt.plot(data_Y[:,-1], label = 'real')
plt.legend()
plt.show()

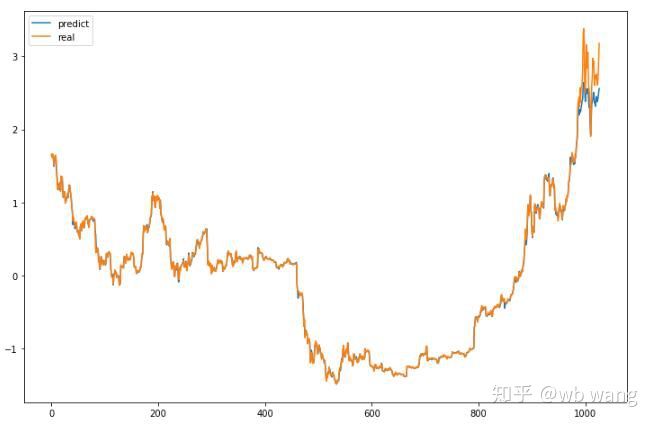
جیسا کہ اعداد و شمار سے دیکھا جا سکتا ہے، تربیتی ڈیٹا کے فٹ ہونے کی ڈگری (800 سے پہلے) بہت زیادہ ہے، لیکن بٹ کوائن کی قیمت بعد میں ایک نئی بلندی پر پہنچ گئی ہے، اور ماڈل نے ان اعداد و شمار کو نہیں دیکھا ہے، لہذا پیشن گوئی یہ ہے اچھی کارکردگی کا مظاہرہ کرنے کے قابل نہیں. اس سے یہ بھی پتہ چلتا ہے کہ پچھلے ڈیٹا کی معیاری کاری میں کوئی مسئلہ تھا۔ اگرچہ پیش گوئی کی گئی قیمت درست نہیں ہو سکتی ہے، لیکن پیشین گوئی کے اعداد و شمار کے ایک حصے پر نظر ڈالیں:

r = data_Y[:,-1][800:1000]
y = p.data.numpy()[800:1000]
r_change = np.array([1 if i > 0 else 0 for i in r[1:200] - r[:199]])
y_change = np.array([1 if i > 0 else 0 for i in y[1:200] - r[:199]])
print((r_change == y_change).sum()/float(len(r_change)))

عروج و زوال کی پیشین گوئی کی درستگی 81.4% تھی، جو میری توقعات سے زیادہ تھی۔ مجھے نہیں معلوم کہ مجھ سے کہیں غلطی ہوئی ہے۔

بلاشبہ، اس ماڈل کی کوئی حقیقی قدر نہیں ہے، لیکن یہ آسان اور سمجھنا آسان ہے، بس اسے ایک نقطہ آغاز کے طور پر استعمال کریں، ڈیجیٹل کرنسی کی مقدار میں عصبی نیٹ ورک کے اطلاق پر مزید تعارفی کورسز ہوں گے۔