Thống kê Bayes là một ngành toán học mạnh mẽ có ứng dụng rộng rãi trong nhiều lĩnh vực, bao gồm tài chính, nghiên cứu y tế và công nghệ thông tin. Nó cho phép chúng ta kết hợp niềm tin trước đó với bằng chứng để đưa ra những niềm tin mới sau này, giúp chúng ta đưa ra quyết định sáng suốt hơn.

Trong bài viết này, chúng tôi sẽ giới thiệu tóm tắt một số nhà toán học chính đã sáng lập ra lĩnh vực này.

Trước Bayes Để hiểu rõ hơn về thống kê Bayes, chúng ta cần quay trở lại thế kỷ 18 và tham khảo nhà toán học De ​​Moivre cùng bài báo “Nguyên lý cơ hội” của ông[1]。

Trong chuyên luận của mình, De Moivre đã đề cập đến nhiều vấn đề của thời đại ông liên quan đến xác suất và cờ bạc. Như bạn có thể biết, giải pháp của ông cho một trong những bài toán này đã dẫn đến nguồn gốc của phân phối chuẩn, nhưng đó lại là một câu chuyện khác.

Trong bài báo của ông có một câu hỏi đơn giản:

“Xác suất nhận được ba mặt ngửa khi tung một đồng xu công bằng ba lần liên tiếp.”

Khi đọc các bài toán được mô tả trong “Nguyên lý ngẫu nhiên”, bạn có thể nhận thấy rằng hầu hết chúng đều bắt đầu bằng một giả thuyết để tính toán xác suất của một sự kiện nhất định. Ví dụ, trong bài toán trên, giả sử đồng xu là đồng xu cân xứng, do đó xác suất ra mặt ngửa khi tung đồng xu là 0,5.

Ngày nay, điều này được diễn đạt bằng thuật ngữ toán học như sau:

𝑃(𝑋|𝜃)

Nhưng nếu chúng ta không biết đồng xu đó có công bằng hay không thì sao? Nếu chúng ta không biết𝜃Vải len?

Thomas Bayes và Richard Price

Gần năm mươi năm sau, vào năm 1763, một bài báo có tựa đề “Một bài luận về nguyên lý ngẫu nhiên”[2] Được công bố trên Tạp chí Triết học của Hội Hoàng gia London.

Trong vài trang đầu của tài liệu, có một đoạn văn do nhà toán học Richard Price viết, tóm tắt nội dung một bài báo do người bạn của ông là Thomas Bayes viết vài năm trước khi ông qua đời. Trong phần giới thiệu, Price giải thích tầm quan trọng của một số khám phá của Thomas Bayes mà không được đề cập trong Nguyên lý ngẫu nhiên của De Moivre.

Trên thực tế, ông đang đề cập đến một vấn đề cụ thể:

“Cho số lần xảy ra và thất bại của một sự kiện chưa biết, hãy tìm cơ hội xảy ra của nó nằm giữa hai mức xác suất được nêu.”

Nói cách khác, sau khi quan sát một sự kiện, chúng ta tìm thấy tham số chưa biếtθXác suất giữa hai mức độ xác suất là bao nhiêu? Trên thực tế, đây là một trong những bài toán đầu tiên trong lịch sử liên quan đến suy luận thống kê và làm nảy sinh tên gọi xác suất nghịch đảo. Về mặt toán học:

𝑃( 𝜃 | 𝑋）

Tất nhiên đây chính là điều mà ngày nay chúng ta gọi là phân phối sau của định lý Bayes.

Nguyên nhân không có nguyên nhân

Hãy làm quen với hai vị mục sư lớn tuổi này.Thomas BayesVàGiá Richard, động lực thúc đẩy nghiên cứu này thực sự rất thú vị. Nhưng để làm được điều này, chúng ta cần dành một chút kiến ​​thức về thống kê sang một bên.

Chúng ta đang ở thế kỷ 18 và xác suất đang trở thành lĩnh vực ngày càng được các nhà toán học quan tâm. Các nhà toán học như De Moivre hay Bernoulli đã chỉ ra rằng một số sự kiện xảy ra với mức độ ngẫu nhiên nhất định nhưng vẫn tuân theo các quy tắc cố định. Ví dụ, nếu bạn tung một con xúc xắc nhiều lần, thì cứ sáu lần bạn sẽ có một lần nó rơi vào số sáu. Giống như có một quy luật ẩn nào đó quyết định số phận của sự ngẫu nhiên.

Bây giờ, hãy tưởng tượng rằng bạn là một nhà toán học và là một tín đồ sùng đạo sống trong thời kỳ này. Bạn có thể quan tâm đến việc quy tắc ẩn này liên quan thế nào đến Chúa.

Đây thực sự là câu hỏi mà chính Bayes và Price đã đặt ra. Giải pháp mà họ hy vọng có thể giải quyết vấn đề này có thể áp dụng trực tiếp để chứng minh rằng “thế giới phải là kết quả của trí tuệ và thông minh; do đó cung cấp bằng chứng cho sự tồn tại của Chúa như một nguyên nhân cuối cùng”[2] - Nghĩa là không có nhân và quả.

Laplace

Thật ngạc nhiên, khoảng hai năm sau, vào năm 1774, rõ ràng là không đọc bài báo của Thomas Bayes, nhà toán học người Pháp Laplace đã viết một bài báo có tựa đề “Về nguyên nhân của các sự kiện thông qua xác suất của các sự kiện”.[3], là một bài báo về vấn đề xác suất nghịch đảo. Ở trang đầu tiên bạn có thể đọc

Các nguyên tắc chính:

“Nếu một sự kiện có thể được gây ra bởi n nguyên nhân khác nhau, thì xác suất của những nguyên nhân này đối với một sự kiện nhất định có tỷ lệ bằng với xác suất của sự kiện khi biết nguyên nhân đó, và xác suất tồn tại của mỗi nguyên nhân này là bằng nhau với xác suất của sự kiện khi có nguyên nhân. Xác suất của các nguyên nhân, chia cho tổng xác suất của sự kiện khi có từng nguyên nhân đó.”

Đây là những gì chúng ta biết ngày nay là định lý Bayes:

​

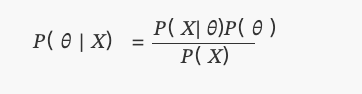
TRONGP(θ)được phân bố đồng đều.

Thí nghiệm đồng xu

Chúng tôi sẽ đưa thống kê Bayesian vào hiện tại bằng cách sử dụng Python và thư viện PyMC và thực hiện một thí nghiệm đơn giản.

Giả sử một người bạn đưa cho bạn một đồng xu và hỏi bạn rằng liệu đó có phải là đồng xu đẹp không. Vì đang vội nên anh ta bảo bạn chỉ tung đồng xu 10 lần thôi. Như bạn có thể thấy, có một tham số chưa biết trong bài toán nàyp, xác suất xuất hiện mặt sấp khi tung đồng xu và chúng ta muốn ước tính điều nàypGiá trị có khả năng xảy ra nhất của .

(Lưu ý: Chúng tôi không nói về các tham sốplà một biến ngẫu nhiên, nhưng tham số này là cố định và chúng ta muốn biết nó có khả năng nằm trong khoảng giá trị nào nhất. )

Để có góc nhìn khác về vấn đề này, chúng ta sẽ giải quyết nó theo hai niềm tin trước đó khác nhau:

• 1. Bạn không có thông tin trước về tính công bằng của đồng tiền và gán xác suất bằng nhau chop. Trong trường hợp này, chúng ta sẽ sử dụng cái gọi là tiên nghiệm không cung cấp thông tin, vì bạn không bổ sung bất kỳ thông tin nào vào niềm tin của mình.
• 1. Bạn biết từ kinh nghiệm rằng ngay cả khi một đồng xu có thể không công bằng, thì cũng khó có thể khiến nó trở nên rất không công bằng, vì vậy bạn nghĩ rằng các thông sốpNhiều khả năng nó sẽ không xuống dưới 0,3 hoặc trên 0,7. Trong trường hợp này, chúng ta sẽ sử dụng thông tin trước.

Đối với cả hai trường hợp, niềm tin trước đó của chúng ta sẽ như sau:

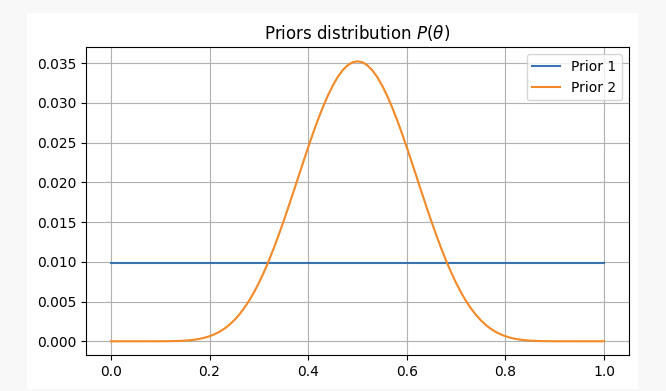
Sau khi tung đồng xu 10 lần, bạn sẽ được 2 mặt ngửa. Với bằng chứng này, chúng ta có thể tìm ra nơi để tìm các tham số của mìnhp？

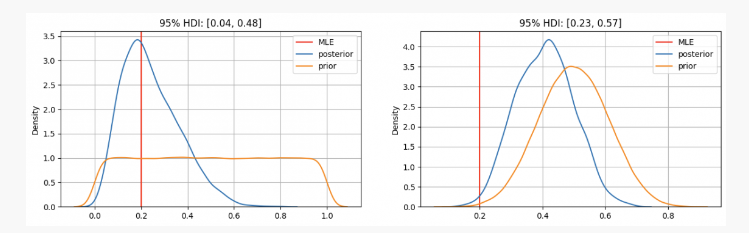
Như bạn có thể thấy, trong trường hợp đầu tiên chúng ta cópPhân phối trước của tập trung vào ước tính khả năng tối đa (MLE)p=0.2, đây là cách tiếp cận tương tự sử dụng phương pháp tần suất. Tham số thực sự chưa biết sẽ nằm trong khoảng tin cậy 95% giữa 0,04 và 0,48.

Mặt khác, khi có độ tin cậy cao rằng tham sốp Trong khi giá trị này phải nằm trong khoảng từ 0,3 đến 0,7, chúng ta có thể thấy rằng phân phối sau là khoảng 0,4, cao hơn nhiều so với giá trị mà MLE của chúng ta đưa ra. Trong trường hợp này, tham số thực sự chưa biết sẽ nằm trong khoảng tin cậy 95% giữa 0,23 và 0,57.

Vì vậy, trong trường hợp đầu tiên, bạn sẽ nói với bạn mình rằng bạn tin chắc đồng xu này không công bằng. Nhưng trong trường hợp khác, bạn sẽ nói với anh ta rằng bạn không chắc liệu đồng xu đó có công bằng hay không.

Như bạn thấy, ngay cả với cùng bằng chứng (2 mặt ngửa trong 10 lần tung), kết quả vẫn có thể khác nhau tùy theo niềm tin trước đó khác nhau. Đây là điểm mạnh của thống kê Bayes, tương tự như phương pháp khoa học, cho phép chúng ta cập nhật niềm tin của mình bằng cách kết hợp niềm tin trước đây với các quan sát và bằng chứng mới.

END

Trong bài viết hôm nay, chúng ta đã tìm hiểu về nguồn gốc của thống kê Bayes và những người đóng góp chính cho thống kê này. Kể từ đó, đã có nhiều người đóng góp quan trọng khác cho lĩnh vực thống kê này (Jeffreys, Cox, Shannon, v.v.), được trích dẫn từ quantdare.com.