রৈখিক রিগ্রেশন - সর্বনিম্ন বর্গ পদ্ধতি

• ### ১, প্রারম্ভিক

এই সময়ের মধ্যে, মেশিনটি শিখতে শিখতে শিখতে শিখতে, অধ্যায় 5 এর লজিস্টিক রিগ্রেশন শিখতে শিখতে এবং এটি বেশ কঠিন মনে হয়েছিল। এই উত্সটি, লজিস্টিক রিগ্রেশন থেকে শুরু করে, লজিস্টিক রিগ্রেশন থেকে শুরু করে, এবং সর্বনিম্ন দ্বিগুণ পদ্ধতিতে। অবশেষে, এটি উচ্চতর গণিতের কোষের (ছয়ম সংস্করণ) অধ্যায় 9 এর দশম অনুচ্ছেদে সর্বনিম্ন দ্বিগুণ পদ্ধতিতে গঠিত হয়েছিল, যা সর্বনিম্ন দ্বিগুণ পদ্ধতির পিছনে গাণিতিক নীতিটি কোথা থেকে এসেছে তা বোঝায়। ন্যূনতম দ্বিগুণ কোষ হল একটি বাস্তবায়ন পদ্ধতি যা অনুকূলিতকরণ সমস্যার মধ্যে অভিজ্ঞতা সূত্র স্থাপন করে। এর নীতিগুলি বোঝার জন্য, লজিস্টিক রিটার্ন কোষ এবং কোষ সমর্থনকারী ভেক্টর মেশিনের শেখার কোষ উভয়ই উপকারী।

• ### দ্বিতীয়, পটভূমি

ন্যূনতম দ্বিগুণ বিভাজক কণার আবির্ভাবের ঐতিহাসিক পটভূমিটি বেশ মজার। (উইকিপিডিয়া থেকে নেওয়া)

১৮০১ সালে, ইতালীয় জ্যোতির্বিজ্ঞানী জুসেপ পিয়াজি প্রথম গ্রহাণু গ্রহাণু আবিষ্কার করেছিলেন। ৪০ দিনের পর্যবেক্ষণের পরে, পিয়াজি তার অবস্থান হারিয়ে ফেলেছিলেন কারণ গ্রহাণু সূর্যের পিছনে চলে গিয়েছিল। পরবর্তীকালে বিশ্বব্যাপী বিজ্ঞানীরা পিয়াজির পর্যবেক্ষণের ডেটা ব্যবহার করে গ্রহাণু খুঁজতে শুরু করেছিলেন, তবে বেশিরভাগ লোকের হিসাবের ভিত্তিতে গ্রহাণু খুঁজতে কোনও ফলাফল পাওয়া যায়নি। সেই সময় ২৪ বছর বয়সী গসও গ্রহাণুর কক্ষপথ গণনা করেছিলেন। অস্ট্রিয়ান জ্যোতির্বিজ্ঞানী হেইরিশ ওলবার্স গস দ্বারা গণনা করা কক্ষপথের ভিত্তিতে গ্রহাণু গ্রহাণু পুনরায় আবিষ্কার করেছিলেন।

গাউসের সর্বনিম্ন দ্বিগুণের পদ্ধতিটি ১৮০৯ সালে তাঁর গ্রন্থে প্রকাশিত হয়েছিল, এবং ফরাসি বিজ্ঞানী লেজেন্ড ১৮০৬ সালে স্বতন্ত্রভাবে সর্বনিম্ন দ্বিগুণের সূত্রটি আবিষ্কার করেছিলেন, তবে অল্প সময়ের জন্য অজ্ঞাত ছিল। দুজনেই সর্বনিম্ন দ্বিগুণের সূত্রটি প্রথম কে প্রতিষ্ঠা করেছিলেন তা নিয়ে বিতর্ক হয়েছিল।

১৮২৯ সালে, গাউস প্রমাণ করেন যে সর্বনিম্ন দ্বিগুণের অপ্টিমাইজেশান অন্যান্য পদ্ধতির চেয়ে বেশি কার্যকর, দেখুন গাউস-মার্কভের উপপাদ্য।

• ### তৃতীয়, জ্ঞান ব্যবহার

সর্বনিম্ন দ্বিগুণ ফ্যাক্টরের মূলটি হল সমস্ত ডেটা বিচ্যুতির বর্গক্ষেত্র এবং সর্বনিম্ন নিশ্চিত করা। ( বর্গক্ষেত্রের প্রাচীনকালে দ্বিগুণ বলা হত)

ধরুন আমরা কিছু যুদ্ধজাহাজের দৈর্ঘ্য এবং প্রস্থের তথ্য সংগ্রহ করেছি।

এই তথ্যের উপর ভিত্তি করে আমরা পাইথন দিয়ে একটি বিক্ষিপ্ত মানচিত্র তৈরি করেছিঃ

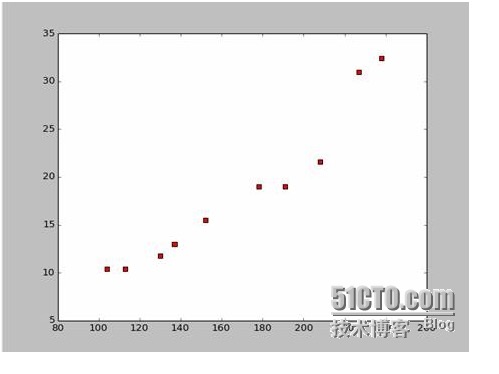
এই কোডটি হলঃ

  import numpy as np                # -*- coding: utf-8 -*
  import os
  import matplotlib.pyplot as plt
  def drawScatterDiagram(fileName): # 改变工作路径到数据文件存放的地方
      os.chdir("d:/workspace_ml")
      xcord=[];ycord=[]
      fr=open(fileName)
      for line in fr.readlines():
          lineArr=line.strip().split()
          xcord.append(float(lineArr[1]));ycord.append(float(lineArr[2]))
      plt.scatter(xcord,ycord,s=30,c='red',marker='s')
      plt.show()

আমরা যদি প্রথম দুইটি পয়েন্ট (২৩৮,৩২.৪) (১৫২,১৫.৫) নিই, তাহলে আমরা দুইটি সমীকরণ পাই। 152*a+b=15.5 328*a+b=32.4 আমরা এই দুটি সমীকরণ সমাধান করি, a=0.197, b=-14.48 এই ক্ষেত্রে, আমরা এই ধরনের একটি সমন্বয় গ্রাফ পেতে পারিঃ

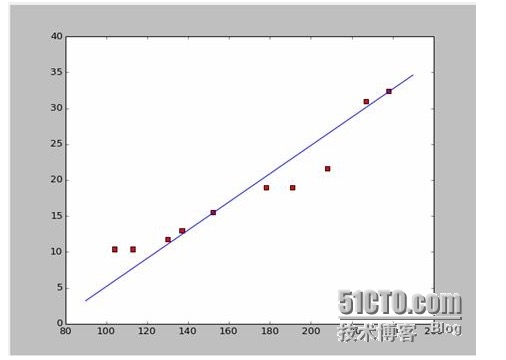
ঠিক আছে, এখন নতুন প্রশ্ন আসে, a এবং b কি সর্বোত্তম সমাধান? পেশাদার ভাষায় বলতে গেলে, a এবং b কি মডেলের সর্বোত্তম প্যারামিটার? এই প্রশ্নের উত্তর দেওয়ার আগে, আমরা আরেকটি প্রশ্ন করিঃ a এবং b কোন শর্ত পূরণ করে?

উত্তর হলঃ গ্যারান্টিযুক্ত সকল তথ্যের স্কয়ার এবং সর্বনিম্ন বিচ্যুতি। নীতিগতভাবে, আমরা পরে আলোচনা করব, কিভাবে এই টুলটি ব্যবহার করে সবচেয়ে ভাল a এবং b গণনা করা যায়।

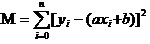
এখন আমরা যা করতে যাচ্ছি তা হল M এর সর্বনিম্ন a এবং b খুঁজে বের করা। লক্ষ্য করুন যে এই সমীকরণে আমরা জানি যে y এবং xi

তাহলে এই সমীকরণটি হচ্ছে একটি দ্বিপদী ফাংশন যেখানে a, b, এবং M, উভয়ই স্ব-পরিবর্তক এবং কারণ-পরিবর্তক।

মনে করে দেখুন কিভাবে উচ্চ সংখ্যার এক-উপায় ফাংশনগুলিকে চূড়ান্ত করা হয়। আমরা এই সরঞ্জামটি ব্যবহার করি। আমরা ডাইরেক্টরি ব্যবহার করি। তবে দ্বিগুণ ফাংশনগুলিতে, আমরা এখনও ডাইরেক্টরি ব্যবহার করি। কেবলমাত্র এখানে ডাইরেক্টরিটির একটি নতুন নাম রয়েছে। ডাইরেক্টরিটি হ’ল দুটি ভেরিয়েবলের মধ্যে একটিকে ধ্রুবক হিসাবে বিবেচনা করা। M এর জন্য প্যারামিটার খুঁজলে আমরা সমীকরণের একটি সেট পাই

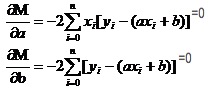
এই দুটি সমীকরণে x এবং y উভয়ই জানা আছে।

এখানে, আমি সরাসরি উত্তরগুলো ব্যবহার করে একটি উপযুক্ত চিত্র আঁকছি, যেহেতু আমরা উইকিপিডিয়া থেকে তথ্য নিয়েছিঃ

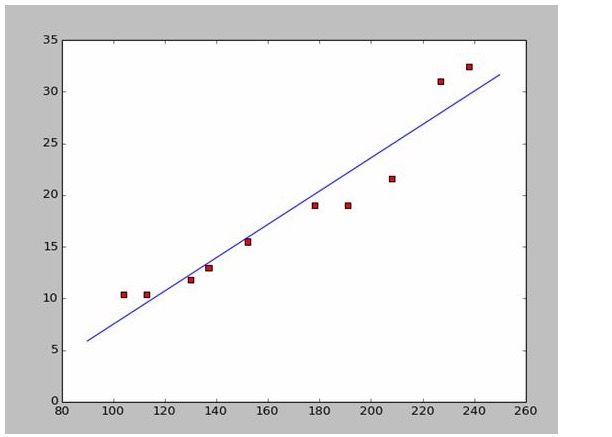
  # -*- coding: utf-8 -*importnumpy as npimportosimportmatplotlib.pyplot as pltdefdrawScatterDiagram(fileName):
  # 改变工作路径到数据文件存放的地方os.chdir("d:/workspace_ml")xcord=[];
  # ycord=[]fr=open(fileName)forline infr.readlines():lineArr=line.strip().split()xcord.append(float(lineArr[1]));
  # ycord.append(float(lineArr[2]))plt.scatter(xcord,ycord,s=30,c='red',marker='s')
  # a=0.1965;b=-14.486a=0.1612;b=-8.6394x=np.arange(90.0,250.0,0.1)y=a*x+bplt.plot(x,y)plt.show()
  # -*- coding: utf-8 -*
  import numpy as np
  import os
  import matplotlib.pyplot as plt
  def drawScatterDiagram(fileName):
      #改变工作路径到数据文件存放的地方
      os.chdir("d:/workspace_ml")
      xcord=[];ycord=[]
      fr=open(fileName)
      for line in fr.readlines():
          lineArr=line.strip().split()
          xcord.append(float(lineArr[1]));ycord.append(float(lineArr[2]))
      plt.scatter(xcord,ycord,s=30,c='red',marker='s')
      #a=0.1965;b=-14.486
      a=0.1612;b=-8.6394
      x=np.arange(90.0,250.0,0.1)
      y=a*x+b
      plt.plot(x,y)
      plt.show()

• ### চারটি নীতি, অনুসন্ধান

ডেটা ফিটনেসে, কেন মডেলের প্যারামিটারগুলিকে অপ্টিমাইজ করার জন্য মডেলের পূর্বাভাসযুক্ত ডেটা এবং প্রকৃত ডেটার মধ্যে পার্থক্যের বর্গক্ষেত্রকে নিখুঁত মান এবং সর্বনিম্নের পরিবর্তে ব্যবহার করা হয়?

এই প্রশ্নের উত্তর ইতিমধ্যে দেওয়া হয়েছে, লিঙ্ক দেখুন (http://blog.sciencenet.cn/blog-430956-621997.html)

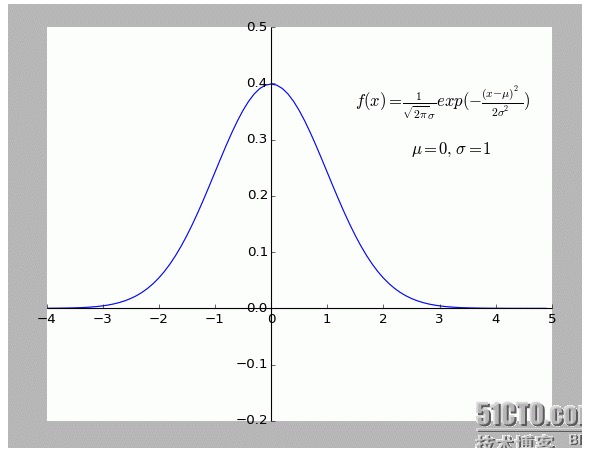
ব্যক্তিগতভাবে এই ব্যাখ্যাটি বেশ আকর্ষণীয় মনে হয়েছে। বিশেষ করে এর ভিতরের অনুমানটিঃ f (x) থেকে বিচ্ছিন্ন সমস্ত বিন্দুতে শব্দ রয়েছে।

একটি বিন্দু যত বেশি দূরে থাকে, তত বেশি গোলমাল হয়, এবং এই বিন্দুটি হওয়ার সম্ভাবনা তত কম। তাহলে বিন্দুটির ঘাটতি x এর সাথে f (x) এর সম্ভাব্যতা সম্পর্কিত কি?

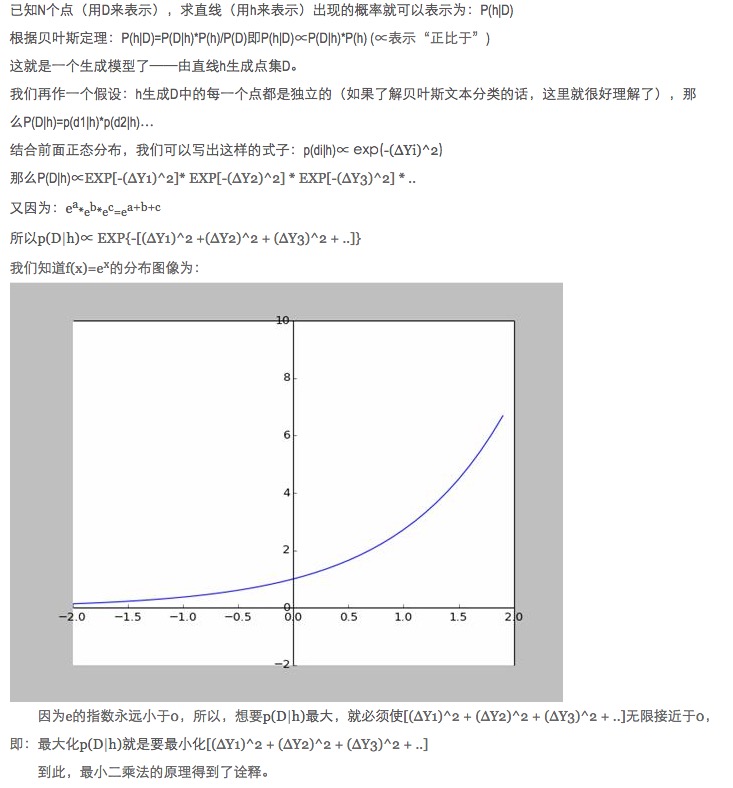
• ### ৫। সম্প্রসারণ

উপরের সবগুলোই দ্বিমাত্রিক পরিস্থিতি, অর্থাৎ শুধুমাত্র একটি স্বতন্ত্র পরিবর্তনশীল রয়েছে। কিন্তু বাস্তব জগতে, চূড়ান্ত ফলাফলের উপর প্রভাব ফেলে এমন অনেকগুলি কারণ রয়েছে, অর্থাৎ স্বতন্ত্র পরিবর্তনশীলগুলির একাধিক পরিস্থিতি থাকতে পারে।

সাধারণ N মেটালাইনরি ফাংশনগুলির জন্য, ক্যালকুলেটরযুক্ত বীজগণিতের প্যাকেটের বিপরীত ম্যাট্রিক্স ব্যবহার করে সমাধান করা ঠিক আছে; যেহেতু সাময়িকভাবে উপযুক্ত উদাহরণ পাওয়া যায় নি, তাই এখানে একটি প্রয়োগ হিসাবে রেখে দেওয়া হয়েছে।

অবশ্যই, প্রকৃতির ক্ষেত্রে, এটি একটি সহজ রৈখিকতা নয়, বরং একটি বহুমুখী সামঞ্জস্য, যা আরও উন্নত।

• তথ্যসূত্র

  • উর্ধ্বতন গণিত বিভাগ (৬ষ্ঠ সংস্করণ)
  • লিনিয়ার অ্যালগরিদম (বিকিং ইউনিভার্সিটি পাবলিসেশন)
  • ইন্টারেক্টিভ এনসাইক্লোপিডিয়াঃসর্বনিম্ন দ্বিগুণ
  • উইকিপিডিয়াঃসর্বনিম্ন দ্বিগুণ পদ্ধতি
  • সাইন্স নেটওয়ার্ক:ন্যূনতম দ্বিগুণ?

মূল রচনা, পুনঃপ্রকাশের অনুমতি, পুনঃপ্রকাশের সময় দয়া করে নিবন্ধের মূল উৎস, লেখকের তথ্য এবং এই বিবৃতিকে হাইপারলিঙ্ক আকারে চিহ্নিত করুন। অন্যথায় আইনী দায়বদ্ধতা থাকবে।http://sbp810050504.blog.51cto.com/2799422/1269572