আমাদের পূর্ববর্তী নিবন্ধে (https://www.fmz.com/digest-topic/4187), আমরা পেয়ার ট্রেডিং কৌশলগুলি প্রবর্তন করেছি এবং প্রদর্শন করেছি কিভাবে ট্রেডিং কৌশলগুলি তৈরি এবং স্বয়ংক্রিয় করতে ডেটা এবং গাণিতিক বিশ্লেষণের সুবিধা নেওয়া যায়।

দীর্ঘ-সংক্ষিপ্ত ভারসাম্যপূর্ণ ইক্যুইটি কৌশল হল পেয়ার ট্রেডিং কৌশলের একটি স্বাভাবিক এক্সটেনশন যা ট্রেডিং বস্তুর একটি ঝুড়িতে প্রযোজ্য। এটি ডিজিটাল মুদ্রা বাজার এবং পণ্য ফিউচার বাজারের মতো অসংখ্য বৈচিত্র্য এবং আন্তঃসম্পর্কযুক্ত ট্রেডিং মার্কেটের জন্য বিশেষভাবে উপযুক্ত।

মৌলিক নীতি

দীর্ঘ-সংক্ষিপ্ত ভারসাম্য ইক্যুইটি কৌশল হল একই সাথে ট্রেডিং লক্ষ্যমাত্রার একটি ঝুড়িতে দীর্ঘ এবং সংক্ষিপ্ত হওয়া। পেয়ার ট্রেডিংয়ের মতোই, কোন বিনিয়োগ লক্ষ্যগুলি সস্তা এবং কোন বিনিয়োগ লক্ষ্যগুলি ব্যয়বহুল তা নির্ধারণ করে যে পার্থক্যটি হল যে কোন বিনিয়োগ লক্ষ্যগুলি তুলনামূলকভাবে সস্তা বা ব্যয়বহুল তা নির্ধারণ করার জন্য দীর্ঘ-সংক্ষিপ্ত ভারসাম্যপূর্ণ ইক্যুইটি স্ট্র্যাটেজি স্টক নির্বাচন পুলে সব বিনিয়োগের লক্ষ্য নির্ধারণ করে৷ . তারপর, এটি র‍্যাঙ্কিংয়ের উপর ভিত্তি করে শীর্ষ n বিনিয়োগ লক্ষ্যগুলিকে দীর্ঘ করবে এবং নীচের n বিনিয়োগ লক্ষ্যগুলিকে সমান পরিমাণে সংক্ষিপ্ত করবে (লং পজিশনের মোট মান = ছোট অবস্থানের মোট মান)।

মনে আছে যখন আমরা বলেছিলাম পেয়ার ট্রেডিং একটি বাজার-নিরপেক্ষ কৌশল? লং-শর্ট ভারসাম্যপূর্ণ ইক্যুইটি কৌশলগুলির ক্ষেত্রেও একই কথা, কারণ সমান পরিমাণে দীর্ঘ এবং ছোট অবস্থান নিশ্চিত করে যে কৌশলটি বাজার নিরপেক্ষ থাকবে (বাজারের ওঠানামা দ্বারা প্রভাবিত হবে না)। কৌশলটি পরিসংখ্যানগতভাবেও শক্তিশালী; বিনিয়োগের র‌্যাঙ্কিং এবং একাধিক অবস্থান ধরে রেখে, আপনি শুধুমাত্র একবারের ঝুঁকির পরিবর্তে আপনার র‌্যাঙ্কিং মডেলের বিপরীতে একাধিক অবস্থান খুলতে পারেন। আপনি যা বাজি ধরছেন তা হল আপনার র্যাঙ্কিং স্কিমের গুণমান।

একটি র্যাঙ্কিং স্কিম কি?

র‌্যাঙ্কিং স্কিম হল এমন মডেল যা প্রত্যাশিত কর্মক্ষমতার উপর ভিত্তি করে প্রতিটি বিনিয়োগকে অগ্রাধিকার প্রদান করে। ফ্যাক্টর হতে পারে মান ফ্যাক্টর, প্রযুক্তিগত সূচক, মূল্যের মডেল বা উপরোক্ত সবগুলির সংমিশ্রণ। উদাহরণ স্বরূপ, আপনি প্রবণতা-অনুসরণকারী বিনিয়োগের একটি সিরিজকে র‌্যাঙ্ক করতে মোমেন্টাম ইন্ডিকেটর ব্যবহার করতে পারেন: সর্বোচ্চ গতিসম্পন্ন বিনিয়োগগুলি ভাল পারফর্ম করতে থাকবে এবং সর্বনিম্ন গতিসম্পন্ন বিনিয়োগগুলি সবচেয়ে খারাপ পারফরমার এবং সর্বনিম্ন হবে বলে আশা করা হয়; রিটার্ন

এই কৌশলটির সাফল্য প্রায় সম্পূর্ণরূপে ব্যবহৃত র‌্যাঙ্কিং স্কিমের মধ্যে নিহিত, অর্থাৎ, আপনার র‌্যাঙ্কিং স্কিম উচ্চ-সম্পাদক বিনিয়োগ লক্ষ্যগুলিকে নিম্ন-সম্পাদক বিনিয়োগ লক্ষ্যগুলি থেকে আলাদা করতে পারে এবং দীর্ঘ-স্বল্প বিনিয়োগ লক্ষ্য কৌশলের আয় আরও ভালভাবে উপলব্ধি করতে পারে। অতএব, একটি র্যাঙ্কিং স্কিম বিকাশ করা খুবই গুরুত্বপূর্ণ।

কিভাবে একটি র্যাঙ্কিং পরিকল্পনা বিকাশ?

একবার আমাদের একটি র‍্যাঙ্কিং স্কিম বের হয়ে গেলে, আমরা অবশ্যই এটি নগদীকরণ করতে সক্ষম হতে চাই। আমরা উপরের বিনিয়োগগুলিকে দীর্ঘ করতে এবং নীচের বিনিয়োগগুলিকে সংক্ষিপ্ত করতে একই পরিমাণ অর্থ বিনিয়োগ করে এটি করি। এটি নিশ্চিত করে যে কৌশলটি শুধুমাত্র র্যাঙ্কিংয়ের গুণমানের অনুপাতে অর্থ উপার্জন করবে এবং “বাজার নিরপেক্ষ” হবে।

ধরুন আপনি সমস্ত বিনিয়োগকে m তে র‍্যাঙ্ক করছেন, বিনিয়োগ করার জন্য n ডলার আছে, এবং মোট 2p (যেখানে m> 2p) পজিশন ধরে রাখতে চান। যদি র‍্যাঙ্ক ১ এর বিনিয়োগ সবচেয়ে খারাপ পারফর্ম করবে বলে আশা করা হয়, তাহলে র‍্যাঙ্ক m এর বিনিয়োগ সবচেয়ে ভালো পারফর্ম করবে বলে আশা করা হচ্ছে:

• আপনি বিনিয়োগের লক্ষ্যগুলি এইভাবে সাজান: 1,…,p, এবং 2/2p মার্কিন ডলারের বিনিয়োগ লক্ষ্যমাত্রা সংক্ষিপ্ত করুন৷

• আপনি বিনিয়োগের লক্ষ্যগুলি এইভাবে সাজান: m-p,…,m, এবং দীর্ঘ n/2p মার্কিন ডলার বিনিয়োগ লক্ষ্যমাত্রা করুন৷

বিজ্ঞপ্তি:যেহেতু মূল্য বৃদ্ধির কারণে বিনিয়োগের লক্ষ্যমাত্রার মূল্য সবসময় n/2p সমানভাবে ভাগ করবে না, এবং কিছু বিনিয়োগ লক্ষ্যমাত্রা অবশ্যই পূর্ণসংখ্যা দিয়ে কিনতে হবে, তাই কিছু অনির্দিষ্ট অ্যালগরিদম থাকবে এবং অ্যালগরিদম যতটা সম্ভব এই সংখ্যার কাছাকাছি হওয়া উচিত। n = 100000 এবং p = 500 চলমান কৌশলটির জন্য, আমরা দেখতে পাই:

n/2p = ¹⁰⁰⁰⁰⁰⁄₁₀₀₀ = 100

এটি 100-এর বেশি দামের ভগ্নাংশের জন্য একটি বড় সমস্যা সৃষ্টি করবে (যেমন কমোডিটি ফিউচার মার্কেট), কারণ আপনি একটি ভগ্নাংশ মূল্যের সাথে একটি অবস্থান খুলতে পারবেন না (ডিজিটাল মুদ্রা বাজারে এই সমস্যাটি বিদ্যমান নেই)। আমরা ভগ্নাংশ মূল্য লেনদেন কমিয়ে বা মূলধন বৃদ্ধি করে এটি প্রশমিত করি।

আসুন একটি অনুমানমূলক উদাহরণ দেখি

• উদ্ভাবক পরিমাণগত প্ল্যাটফর্মে আমাদের গবেষণা পরিবেশ তৈরি করুন

প্রথমত, সুষ্ঠুভাবে কাজ করার জন্য, আমাদের গবেষণার পরিবেশ তৈরি করতে হবে। এই প্রবন্ধে, আমরা গবেষণার পরিবেশ তৈরি করতে Inventor Quantitative Platform (FMZ.COM) ব্যবহার করব, মূলত যাতে আমরা সুবিধাজনক এবং দ্রুত API ব্যবহার করতে পারি। এই প্ল্যাটফর্মের ইন্টারফেস এবং এনক্যাপসুলেশন পরে। সম্পূর্ণ ডকার সিস্টেম।

উদ্ভাবক কোয়ান্টিফিকেশন প্ল্যাটফর্মের অফিসিয়াল নামে, এই ডকার সিস্টেমটিকে হোস্ট সিস্টেম বলা হয়।

কিভাবে হোস্ট এবং রোবট স্থাপন করতে হয়, অনুগ্রহ করে আমার আগের নিবন্ধটি পড়ুন: https://www.fmz.com/bbs-topic/4140

যে পাঠকরা তাদের নিজস্ব ক্লাউড কম্পিউটিং সার্ভার স্থাপনার হোস্টার কিনতে চান তারা এই নিবন্ধটি উল্লেখ করতে পারেন: https://www.fmz.com/bbs-topic/2848

ক্লাউড কম্পিউটিং পরিষেবা এবং হোস্ট সিস্টেম সফলভাবে স্থাপন করার পরে, পরবর্তী, আমাদের পাইথনের বৃহত্তম শিল্পকর্মটি ইনস্টল করতে হবে: অ্যানাকোন্ডা

এই নিবন্ধটির জন্য প্রয়োজনীয় সমস্ত প্রাসঙ্গিক প্রোগ্রামিং পরিবেশ বাস্তবায়নের জন্য (নির্ভরতা লাইব্রেরি, সংস্করণ ব্যবস্থাপনা, ইত্যাদি), সবচেয়ে সহজ উপায় হল Anaconda ব্যবহার করা। এটি একটি প্যাকেজড পাইথন ডেটা সায়েন্স ইকোসিস্টেম এবং নির্ভরতা লাইব্রেরি ম্যানেজার।

অ্যানাকোন্ডার ইনস্টলেশন পদ্ধতির জন্য, অনুগ্রহ করে অ্যানাকোন্ডার অফিসিয়াল গাইডটি দেখুন: https://www.anaconda.com/distribution/

এই প্রবন্ধে পাইথন বৈজ্ঞানিক কম্পিউটিংয়ে দুটি অত্যন্ত জনপ্রিয় এবং গুরুত্বপূর্ণ লাইব্রেরি, নম্পি এবং পান্ডাসও ব্যবহার করা হবে।

উপরের মৌলিক কাজের জন্য, আপনি আমার পূর্ববর্তী নিবন্ধটিও উল্লেখ করতে পারেন, যেটিতে অ্যানাকোন্ডা পরিবেশ এবং নম্পি এবং পান্ডাগুলির দুটি লাইব্রেরি কীভাবে সেট আপ করতে হয় তার একটি ভূমিকা রয়েছে, দয়া করে দেখুন: https://www.fmz। com/digest-topic/4169

আমরা এলোমেলো বিনিয়োগ লক্ষ্যমাত্রা এবং এলোমেলো কারণগুলি তৈরি করি এবং সেগুলিকে র‌্যাঙ্ক করি। আসুন ধরে নিই যে আমাদের ভবিষ্যত আয় আসলে এই ফ্যাক্টর মানগুলির উপর নির্ভর করে।

import numpy as np
import statsmodels.api as sm
import scipy.stats as stats
import scipy
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
## PROBLEM SETUP ##
# Generate stocks and a random factor value for them
stock_names = ['stock ' + str(x) for x in range(10000)]
current_factor_values = np.random.normal(0, 1, 10000)
# Generate future returns for these are dependent on our factor values
future_returns = current_factor_values + np.random.normal(0, 1, 10000)
# Put both the factor values and returns into one dataframe
data = pd.DataFrame(index = stock_names, columns=['Factor Value','Returns'])
data['Factor Value'] = current_factor_values
data['Returns'] = future_returns
# Take a look
data.head(10)

এখন যেহেতু আমাদের ফ্যাক্টর ভ্যালু এবং রিটার্ন আছে, আমরা দেখতে পারি যদি আমরা ফ্যাক্টর মানের উপর ভিত্তি করে বিনিয়োগকে র‍্যাঙ্ক করি এবং তারপর লং এবং ছোট পজিশন খুলি তাহলে কী হবে।

# Rank stocks
ranked_data = data.sort_values('Factor Value')
# Compute the returns of each basket with a basket size 500, so total (10000/500) baskets
number_of_baskets = int(10000/500)
basket_returns = np.zeros(number_of_baskets)
for i in range(number_of_baskets):
    start = i * 500
    end = i * 500 + 500 
    basket_returns[i] = ranked_data[start:end]['Returns'].mean()
# Plot the returns of each basket
plt.figure(figsize=(15,7))
plt.bar(range(number_of_baskets), basket_returns)
plt.ylabel('Returns')
plt.xlabel('Basket')
plt.legend(['Returns of Each Basket'])
plt.show()

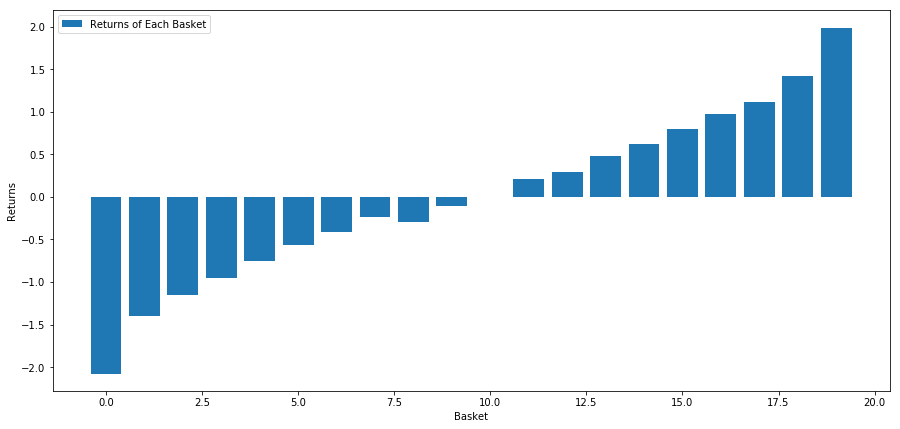
আমাদের কৌশল হল একটি ঝুড়িতে এক নম্বর বিনিয়োগ লক্ষ্যে দীর্ঘ এবং 10তম লক্ষ্যে সংক্ষিপ্ত হওয়া। এই কৌশলটির জন্য অর্থ প্রদান হল:

basket_returns[number_of_baskets-1] - basket_returns[0]

ফলাফল হল: 4.172

উচ্চ-কর্মক্ষমতাসম্পন্ন বিনিয়োগ এবং নিম্ন-কর্মক্ষমতাসম্পন্ন বিনিয়োগকে আলাদা করতে আমাদের র‍্যাঙ্কিং মডেলে আপনার অর্থ বিনিয়োগ করুন।

এই প্রবন্ধের বাকি অংশে, আমরা আলোচনা করব কিভাবে র‍্যাঙ্কিং স্কিম মূল্যায়ন করতে হয়। র‍্যাঙ্কিং-ভিত্তিক আরবিট্রেজ থেকে অর্থ উপার্জনের সুবিধা হল এটি বাজারের ব্যাধি দ্বারা প্রভাবিত হয় না, বরং এর সুবিধা নিতে পারে।

আসুন একটি বাস্তব বিশ্বের উদাহরণ বিবেচনা করা যাক।

আমরা S&P 500-এ বিভিন্ন শিল্পে 32টি স্টকের জন্য ডেটা লোড করেছি এবং তাদের র‌্যাঙ্ক করার চেষ্টা করেছি।

from backtester.dataSource.yahoo_data_source import YahooStockDataSource
from datetime import datetime
startDateStr = '2010/01/01'
endDateStr = '2017/12/31'
cachedFolderName = '/Users/chandinijain/Auquan/yahooData/'
dataSetId = 'testLongShortTrading'
instrumentIds = ['ABT','AKS','AMGN','AMD','AXP','BK','BSX',
                'CMCSA','CVS','DIS','EA','EOG','GLW','HAL',
                'HD','LOW','KO','LLY','MCD','MET','NEM',
                'PEP','PG','M','SWN','T','TGT',
                'TWX','TXN','USB','VZ','WFC']
ds = YahooStockDataSource(cachedFolderName=cachedFolderName,
                            dataSetId=dataSetId,
                            instrumentIds=instrumentIds,
                            startDateStr=startDateStr,
                            endDateStr=endDateStr,
                            event='history')
price = 'adjClose'

চলুন এক মাসের সময়সীমার স্বাভাবিক গতির সূচকের উপর ভিত্তি করে র‌্যাঙ্ক করি

## Define normalized momentum
def momentum(dataDf, period):
    return dataDf.sub(dataDf.shift(period), fill_value=0) / dataDf.iloc[-1]
## Load relevant prices in a dataframe
data = ds.getBookDataByFeature()[‘Adj Close’]
#Let's load momentum score and returns into separate dataframes
index = data.index
mscores = pd.DataFrame(index=index,columns=assetList)
mscores = momentum(data, 30)
returns = pd.DataFrame(index=index,columns=assetList)
day = 30

এখন আমরা আমাদের স্টকের আচরণ বিশ্লেষণ করব এবং আমাদের নির্বাচিত র‌্যাঙ্কিং ফ্যাক্টরগুলির মধ্যে আমাদের স্টক বাজারে কীভাবে পারফর্ম করে তা দেখব।

তথ্য বিশ্লেষণ করুন

স্টক আচরণ

আমরা আমাদের র্যাঙ্কিং মডেলে আমাদের নির্বাচিত বাস্কেট স্টকগুলি কীভাবে সঞ্চালন করে তা দেখি। এটি করার জন্য, আসুন সমস্ত স্টকের জন্য এক সপ্তাহের ফরোয়ার্ড রিটার্ন গণনা করি। তারপরে আমরা 30 দিনের আগের গতির সাথে প্রতিটি স্টকের 1-সপ্তাহের ফরোয়ার্ড রিটার্নের পারস্পরিক সম্পর্ক দেখতে পারি। যে স্টকগুলি ইতিবাচক পারস্পরিক সম্পর্ক প্রদর্শন করে সেগুলি হল প্রবণতা অনুসরণ করা, এবং যে স্টকগুলি নেতিবাচক পারস্পরিক সম্পর্ক প্রদর্শন করে সেগুলি হল প্রত্যাবর্তন৷

# Calculate Forward returns
forward_return_day = 5
returns = data.shift(-forward_return_day)/data -1
returns.dropna(inplace = True)
# Calculate correlations between momentum and returns
correlations = pd.DataFrame(index = returns.columns, columns = [‘Scores’, ‘pvalues’])
mscores = mscores[mscores.index.isin(returns.index)]
for i in correlations.index:
    score, pvalue = stats.spearmanr(mscores[i], returns[i])
    correlations[‘pvalues’].loc[i] = pvalue
    correlations[‘Scores’].loc[i] = score
correlations.dropna(inplace = True)
correlations.sort_values(‘Scores’, inplace=True)
l = correlations.index.size
plt.figure(figsize=(15,7))
plt.bar(range(1,1+l),correlations[‘Scores’])
plt.xlabel(‘Stocks’)
plt.xlim((1, l+1))
plt.xticks(range(1,1+l), correlations.index)
plt.legend([‘Correlation over All Data’])
plt.ylabel(‘Correlation between %s day Momentum Scores and %s-day forward returns by Stock’%(day,forward_return_day));
plt.show()

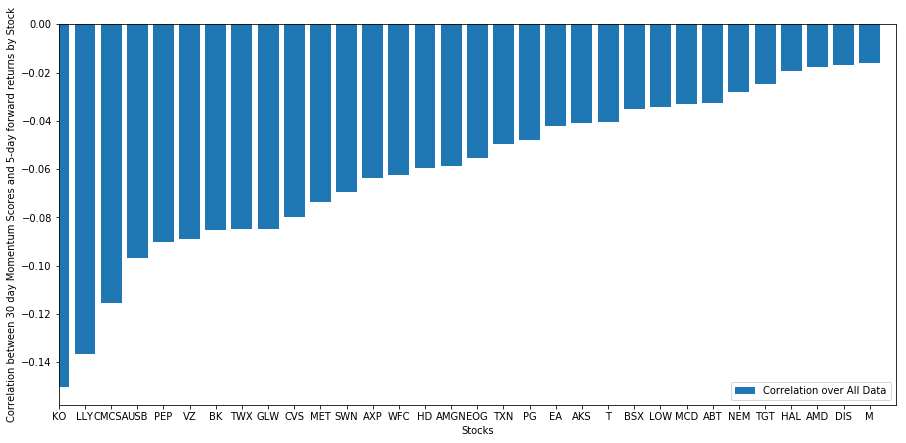
আমাদের স্টক সব কিছু ডিগ্রী ফিরে মানে! (আপাতদৃষ্টিতে এইভাবে আমাদের নির্বাচিত মহাবিশ্ব কাজ করে) এটি আমাদের বলে যে যদি একটি স্টক মোমেন্টাম বিশ্লেষণে উচ্চ স্কোর করে, তাহলে আমাদের আশা করা উচিত যে এটি পরের সপ্তাহে কম পারফর্ম করবে।

মোমেন্টাম স্কোর র‍্যাঙ্কিং এবং রিটার্নের মধ্যে সম্পর্ক

এর পরে, আমাদের আমাদের র‌্যাঙ্কিং স্কোর এবং বাজারের সামগ্রিক ফরওয়ার্ড রিটার্নের মধ্যে পারস্পরিক সম্পর্ক দেখতে হবে, অর্থাৎ আমাদের র‌্যাঙ্কিং ফ্যাক্টরের সাপেক্ষে প্রত্যাশিত রিটার্নের ভবিষ্যদ্বাণী, এবং উচ্চতর পারস্পরিক সম্পর্ক রেটিং দরিদ্র আপেক্ষিক রিটার্নের পূর্বাভাস দেয়, নাকি এর বিপরীতে?

এটি করার জন্য, আমরা সমস্ত স্টকের জন্য 30-দিনের গতি এবং 1-সপ্তাহের ফরোয়ার্ড রিটার্নের মধ্যে দৈনিক পারস্পরিক সম্পর্ক গণনা করি।

correl_scores = pd.DataFrame(index = returns.index.intersection(mscores.index), columns = [‘Scores’, ‘pvalues’])
for i in correl_scores.index:
    score, pvalue = stats.spearmanr(mscores.loc[i], returns.loc[i])
    correl_scores[‘pvalues’].loc[i] = pvalue
    correl_scores[‘Scores’].loc[i] = score
correl_scores.dropna(inplace = True)
l = correl_scores.index.size
plt.figure(figsize=(15,7))
plt.bar(range(1,1+l),correl_scores[‘Scores’])
plt.hlines(np.mean(correl_scores[‘Scores’]), 1,l+1, colors=’r’, linestyles=’dashed’)
plt.xlabel(‘Day’)
plt.xlim((1, l+1))
plt.legend([‘Mean Correlation over All Data’, ‘Daily Rank Correlation’])
plt.ylabel(‘Rank correlation between %s day Momentum Scores and %s-day forward returns’%(day,forward_return_day));
plt.show()

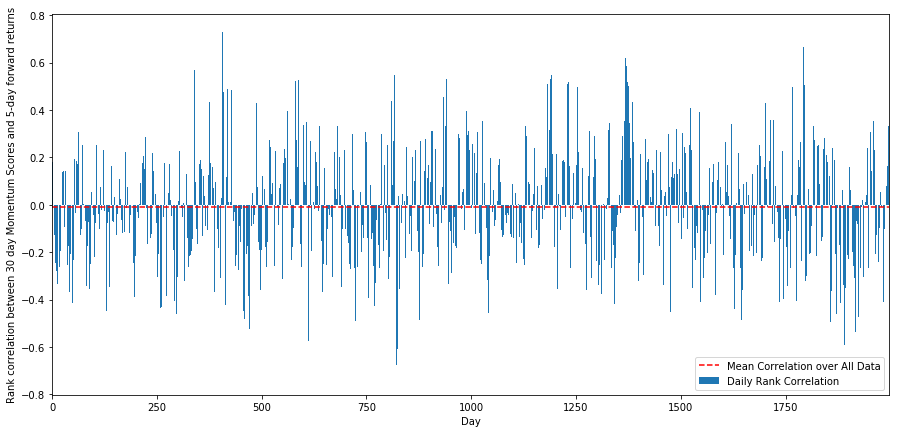
দৈনিক পারস্পরিক সম্পর্ক খুব গোলমেলে, কিন্তু খুব সামান্য (এটি প্রত্যাশিত যেহেতু আমরা বলেছি যে সমস্ত স্টক মানে প্রত্যাবর্তন)। আমরা 1 মাসের ফরোয়ার্ড রিটার্নের গড় মাসিক পারস্পরিক সম্পর্কও দেখি।

monthly_mean_correl =correl_scores['Scores'].astype(float).resample('M').mean()
plt.figure(figsize=(15,7))
plt.bar(range(1,len(monthly_mean_correl)+1), monthly_mean_correl)
plt.hlines(np.mean(monthly_mean_correl), 1,len(monthly_mean_correl)+1, colors='r', linestyles='dashed')
plt.xlabel('Month')
plt.xlim((1, len(monthly_mean_correl)+1))
plt.legend(['Mean Correlation over All Data', 'Monthly Rank Correlation'])
plt.ylabel('Rank correlation between %s day Momentum Scores and %s-day forward returns'%(day,forward_return_day));
plt.show()

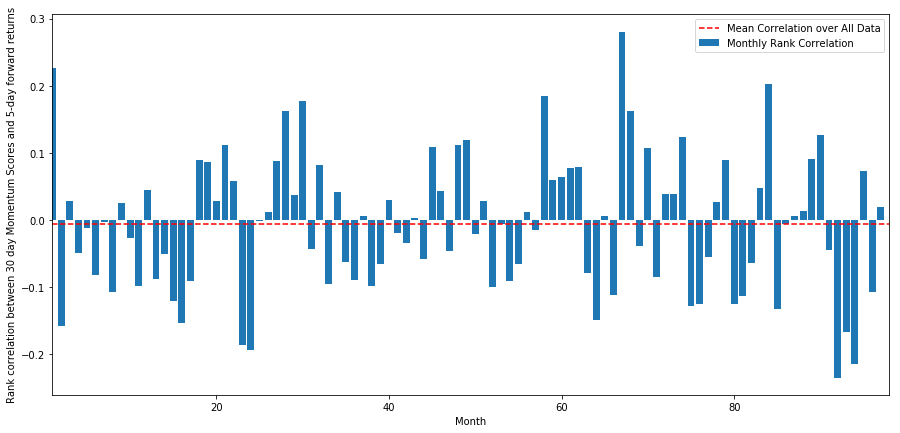
আমরা দেখতে পাচ্ছি যে গড় পারস্পরিক সম্পর্ক আবার সামান্য নেতিবাচক, তবে মাস থেকে মাসেও অনেক পরিবর্তিত হয়।

গড় স্টক রিটার্নের ঝুড়ি

আমরা আমাদের র‌্যাঙ্কিং থেকে নেওয়া স্টকের ঝুড়ির জন্য রিটার্ন গণনা করেছি। আমরা যদি সমস্ত স্টককে র‍্যাঙ্ক করি এবং তারপর এন গ্রুপে ভাগ করি, তাহলে প্রতিটি গ্রুপের গড় রিটার্ন কত?

প্রথম ধাপ হল একটি ফাংশন তৈরি করা যা প্রতি মাসে দেওয়া প্রতিটি ঝুড়ির জন্য গড় রিটার্ন এবং র‌্যাঙ্কিং ফ্যাক্টর দেবে।

def compute_basket_returns(factor, forward_returns, number_of_baskets, index):
data = pd.concat([factor.loc[index],forward_returns.loc[index]], axis=1)
    # Rank the equities on the factor values
    data.columns = ['Factor Value', 'Forward Returns']
    data.sort_values('Factor Value', inplace=True)
    # How many equities per basket
    equities_per_basket = np.floor(len(data.index) / number_of_baskets)
basket_returns = np.zeros(number_of_baskets)
# Compute the returns of each basket
    for i in range(number_of_baskets):
        start = i * equities_per_basket
        if i == number_of_baskets - 1:
            # Handle having a few extra in the last basket when our number of equities doesn't divide well
            end = len(data.index) - 1
        else:
            end = i * equities_per_basket + equities_per_basket
        # Actually compute the mean returns for each basket
        #s = data.index.iloc[start]
        #e = data.index.iloc[end]
        basket_returns[i] = data.iloc[int(start):int(end)]['Forward Returns'].mean()
        
    return basket_returns

এই স্কোরের উপর ভিত্তি করে স্টক র‍্যাঙ্কিং করার সময় আমরা প্রতিটি ঝুড়ির জন্য গড় রিটার্ন গণনা করি। এটি আমাদের দীর্ঘ সময় ধরে তাদের সম্পর্কের একটি আভাস দেওয়া উচিত।

number_of_baskets = 8
mean_basket_returns = np.zeros(number_of_baskets)
resampled_scores = mscores.astype(float).resample('2D').last()
resampled_prices = data.astype(float).resample('2D').last()
resampled_scores.dropna(inplace=True)
resampled_prices.dropna(inplace=True)
forward_returns = resampled_prices.shift(-1)/resampled_prices -1
forward_returns.dropna(inplace = True)
for m in forward_returns.index.intersection(resampled_scores.index):
    basket_returns = compute_basket_returns(resampled_scores, forward_returns, number_of_baskets, m)
    mean_basket_returns += basket_returns
mean_basket_returns /= l    
print(mean_basket_returns)
# Plot the returns of each basket
plt.figure(figsize=(15,7))
plt.bar(range(number_of_baskets), mean_basket_returns)
plt.ylabel('Returns')
plt.xlabel('Basket')
plt.legend(['Returns of Each Basket'])
plt.show()

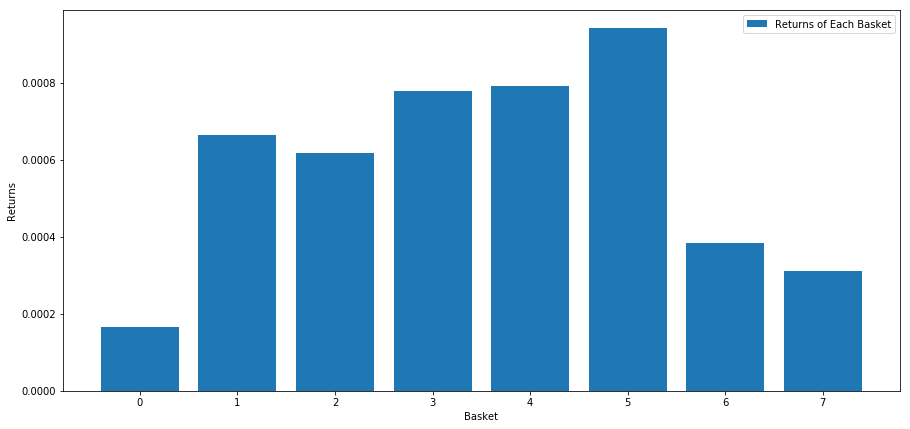
মনে হচ্ছে আমরা উচ্চ পারফরমারদের থেকে কম পারফর্মারদের আলাদা করতে পারি।

স্প্রেড (ভিত্তি) ধারাবাহিকতা

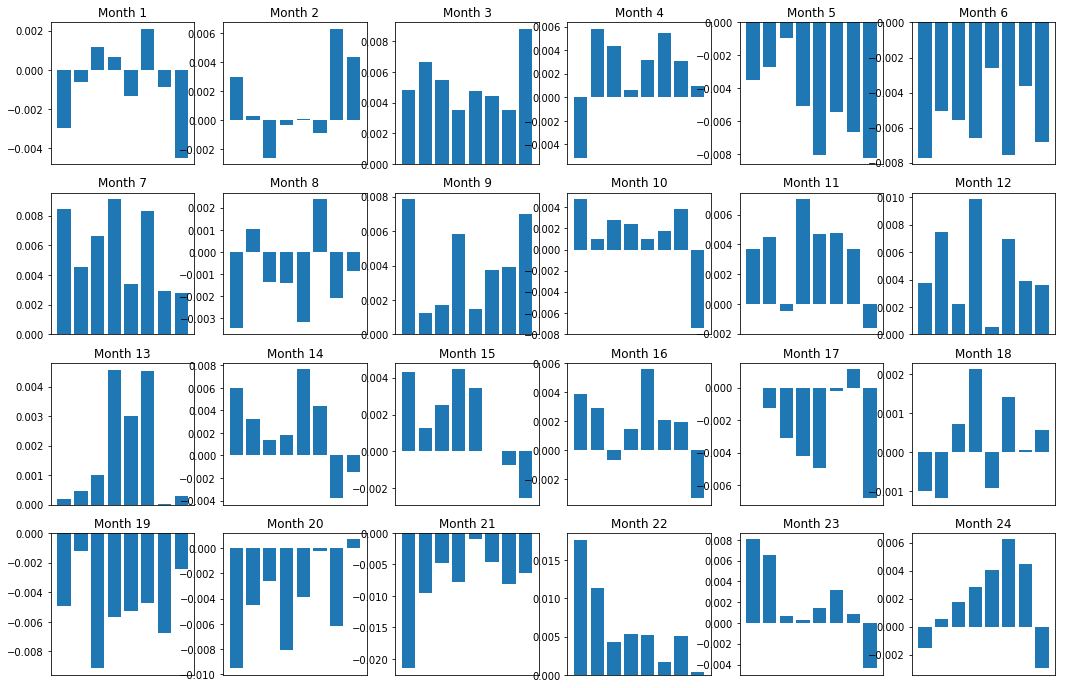
অবশ্যই, এগুলি কেবল গড় সম্পর্ক। সম্পর্কটি কতটা সামঞ্জস্যপূর্ণ এবং আমরা এটি বাণিজ্য করতে ইচ্ছুক কিনা তা বোঝার জন্য, সময়ের সাথে সাথে আমাদের এটির প্রতি আমাদের দৃষ্টিভঙ্গি এবং মনোভাব পরিবর্তন করা উচিত। এর পরে, আমরা আগের দুই বছরের জন্য তাদের মাসিক স্প্রেড (ভিত্তি) দেখব। এই মোমেন্টাম স্কোরটি ট্রেডযোগ্য কিনা তা নির্ধারণ করতে আমরা আরও পরিবর্তন দেখতে পারি এবং আরও বিশ্লেষণ পরিচালনা করতে পারি।

total_months = mscores.resample('M').last().index
months_to_plot = 24
monthly_index = total_months[:months_to_plot+1]
mean_basket_returns = np.zeros(number_of_baskets)
strategy_returns = pd.Series(index = monthly_index)
f, axarr = plt.subplots(1+int(monthly_index.size/6), 6,figsize=(18, 15))
for month in range(1, monthly_index.size):
    temp_returns = forward_returns.loc[monthly_index[month-1]:monthly_index[month]]
    temp_scores = resampled_scores.loc[monthly_index[month-1]:monthly_index[month]]
    for m in temp_returns.index.intersection(temp_scores.index):
        basket_returns = compute_basket_returns(temp_scores, temp_returns, number_of_baskets, m)
        mean_basket_returns += basket_returns
    
    strategy_returns[monthly_index[month-1]] = mean_basket_returns[ number_of_baskets-1] - mean_basket_returns[0]
    
    mean_basket_returns /= temp_returns.index.intersection(temp_scores.index).size
    
    r = int(np.floor((month-1) / 6))
    c = (month-1) % 6
    axarr[r, c].bar(range(number_of_baskets), mean_basket_returns)
    axarr[r, c].xaxis.set_visible(False)
    axarr[r, c].set_title('Month ' + str(month))
plt.show()

plt.figure(figsize=(15,7))
plt.plot(strategy_returns)
plt.ylabel(‘Returns’)
plt.xlabel(‘Month’)
plt.plot(strategy_returns.cumsum())
plt.legend([‘Monthly Strategy Returns’,’Cumulative Strategy Returns’])
plt.show()

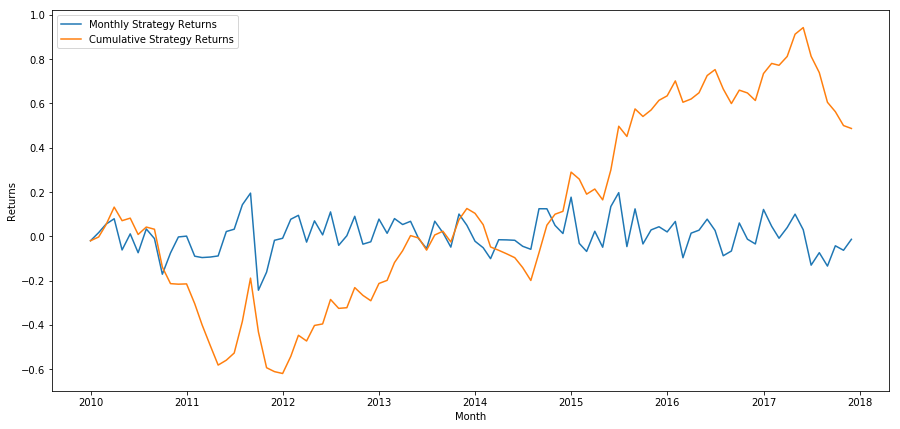
পরিশেষে, আসুন আমরা যদি শেষ ঝুড়িটি দীর্ঘ করি এবং প্রতি মাসে প্রথম ঝুড়িটি সংক্ষিপ্ত করি (প্রতিটি সিকিউরিটির জন্য সমান মূলধন বরাদ্দ ধরে নিই) তাহলে আয়ের দিকে তাকাই।

total_return = strategy_returns.sum()
ann_return = 100*((1 + total_return)**(12.0 /float(strategy_returns.index.size))-1)
print('Annual Returns: %.2f%%'%ann_return)

বার্ষিক রিটার্ন: 5.03%

আমরা দেখতে পাচ্ছি যে আমাদের একটি খুব দুর্বল র‌্যাঙ্কিং স্কিম রয়েছে যা শুধুমাত্র নিম্ন-কার্যকারি স্টক থেকে উচ্চ-কার্যকারি স্টকগুলিকে পরিমিতভাবে আলাদা করে। উপরন্তু, এই র‌্যাঙ্কিং স্কিমটিতে কোন ধারাবাহিকতা নেই এবং এটি মাসে মাসে উল্লেখযোগ্যভাবে পরিবর্তিত হয়।

সঠিক র‍্যাঙ্কিং স্কিম খোঁজা

একটি দীর্ঘ-সংক্ষিপ্ত ভারসাম্যপূর্ণ ইক্যুইটি কৌশল বাস্তবায়ন করতে, আপনাকে সত্যিই শুধুমাত্র একটি র‌্যাঙ্কিং স্কিম নির্ধারণ করতে হবে। তার পরের সবকিছুই যান্ত্রিক। একবার আপনার একটি দীর্ঘ-সংক্ষিপ্ত ভারসাম্যপূর্ণ ইক্যুইটি কৌশল থাকলে, আপনি অন্য কিছু পরিবর্তন না করেই বিভিন্ন র‌্যাঙ্কিং ফ্যাক্টর অদলবদল করতে পারেন। প্রতিবার পুরো কোড সামঞ্জস্য করার বিষয়ে চিন্তা না করেই আপনার ধারণাগুলিকে দ্রুত পুনরাবৃত্তি করার এটি একটি খুব সুবিধাজনক উপায়।

র‍্যাঙ্কিং স্কিমগুলি প্রায় যে কোনও মডেল থেকেও আসতে পারে। এটি একটি মান-ভিত্তিক ফ্যাক্টর মডেল হতে হবে না, এটি একটি মেশিন লার্নিং কৌশল হতে পারে যা এক মাস আগে রিটার্নের ভবিষ্যদ্বাণী করে এবং সেই রেটিং এর উপর ভিত্তি করে তাদের র‍্যাঙ্ক করে।

র‌্যাঙ্কিং স্কিম নির্বাচন এবং মূল্যায়ন

র‌্যাঙ্কিং স্কিম হল সুবিধা এবং দীর্ঘ-সংক্ষিপ্ত ভারসাম্যপূর্ণ ইক্যুইটি কৌশলের সবচেয়ে গুরুত্বপূর্ণ উপাদান। একটি ভাল র‍্যাঙ্কিং স্কিম বেছে নেওয়া একটি নিয়মতান্ত্রিক প্রকল্প এবং এর কোন সহজ উত্তর নেই।

একটি ভাল সূচনা বিন্দু হল বিদ্যমান, পরিচিত কৌশলগুলি গ্রহণ করা এবং উচ্চ রিটার্ন পাওয়ার জন্য আপনি সেগুলিকে সামান্য পরিবর্তন করতে পারেন কিনা তা দেখুন। আমরা এখানে কয়েকটি শুরুর পয়েন্ট নিয়ে আলোচনা করব:

• ক্লোন করুন এবং সামঞ্জস্য করুন: এমন কিছু বেছে নিন যা প্রায়শই আলোচিত হয় এবং দেখুন আপনি আপনার সুবিধার জন্য এটিকে কিছুটা পরিবর্তন করতে পারেন কিনা। সাধারণত, পাবলিক ফ্যাক্টরগুলিতে আর ট্রেডিং সিগন্যাল থাকবে না কারণ সেগুলি সম্পূর্ণরূপে বাজার থেকে বেরিয়ে গেছে। তবে, কখনও কখনও তারা আপনাকে সঠিক পথে পরিচালিত করতে পারে।

• দামের মডেল: ভবিষ্যতের রিটার্নের ভবিষ্যদ্বাণী করে এমন যেকোন মডেল একটি ফ্যাক্টর হতে পারে, সম্ভাব্যভাবে আপনার ব্যবসার ঝুড়ি র‌্যাঙ্ক করতে ব্যবহৃত হয়। আপনি যেকোনো জটিল মূল্যের মডেল নিতে পারেন এবং এটিকে একটি র‌্যাঙ্কিং স্কিমে রূপান্তর করতে পারেন।

• মূল্য-ভিত্তিক কারণ (প্রযুক্তিগত সূচক): মূল্য-ভিত্তিক ফ্যাক্টরগুলি, যেমন আমরা আজ আলোচনা করেছি, প্রতিটি ইকুইটির ঐতিহাসিক মূল্য সম্পর্কে তথ্য গ্রহণ করে এবং একটি ফ্যাক্টর মান তৈরি করতে এটি ব্যবহার করে। উদাহরণ হিসেবে বলা যেতে পারে চলমান গড় সূচক, ভরবেগ সূচক অথবা অস্থিরতা সূচক।

• রিগ্রেশন এবং মোমেন্টাম: এটা লক্ষণীয় যে কিছু কারণ বিশ্বাস করে যে একবার দাম এক দিকে চলে গেলে, তারা তা করতে থাকবে। কিছু কারণ ঠিক বিপরীত কাজ. উভয়ই বিভিন্ন সময় ফ্রেম এবং সম্পদের বৈধ মডেল, এবং অন্তর্নিহিত আচরণটি ভরবেগ-ভিত্তিক বা রিগ্রেশন-ভিত্তিক কিনা তা তদন্ত করা গুরুত্বপূর্ণ।

• মৌলিক কারণ (মূল্য ভিত্তিক): এটি PE, লভ্যাংশ ইত্যাদির মতো মৌলিক মানগুলির সংমিশ্রণ ব্যবহার করছে। মৌলিক মূল্যের মধ্যে একটি কোম্পানি সম্পর্কে বাস্তব তথ্য সম্পর্কিত তথ্য থাকে এবং তাই এটি অনেক দিক থেকে মূল্যের চেয়ে বেশি শক্তিশালী হতে পারে।

শেষ পর্যন্ত, ভবিষ্যদ্বাণী করা একটি অস্ত্রের প্রতিযোগিতা এবং আপনি এক ধাপ এগিয়ে থাকার চেষ্টা করছেন। ফ্যাক্টরগুলি বাজার থেকে সালিশ করা হয় এবং একটি দরকারী জীবন থাকে, তাই আপনার ফ্যাক্টরগুলি কতটা ক্ষয়প্রাপ্ত হয়েছে এবং সেগুলি প্রতিস্থাপন করতে কোন নতুন কারণগুলি ব্যবহার করা যেতে পারে তা নির্ধারণ করার জন্য আপনাকে ক্রমাগত কাজ করতে হবে।

অন্যান্য বিবেচনা

• ভারসাম্য ফ্রিকোয়েন্সি

প্রতিটি র‍্যাঙ্কিং সিস্টেম সামান্য ভিন্ন সময়ের ফ্রেমে রিটার্নের পূর্বাভাস দেয়। মূল্য-ভিত্তিক গড় প্রত্যাবর্তন দিনের মধ্যে অনুমানযোগ্য হতে পারে, যখন মান-ভিত্তিক ফ্যাক্টর মডেলগুলি কয়েক মাসের মধ্যে ভবিষ্যদ্বাণীমূলক হতে পারে। কৌশলটি কার্যকর করার আগে মডেলটির ভবিষ্যদ্বাণী করা এবং পরিসংখ্যানগত বৈধতা সম্পাদন করা উচিত তা নির্ধারণ করা গুরুত্বপূর্ণ। আপনি অবশ্যই রিব্যালেন্সিং ফ্রিকোয়েন্সি অপ্টিমাইজ করার চেষ্টা করে ওভারফিট করতে চান না, আপনি অনিবার্যভাবে একটি ফ্রিকোয়েন্সি খুঁজে পাবেন যা অন্যদের থেকে এলোমেলোভাবে ভালো। আপনার মডেলের মধ্যে সবচেয়ে বেশি।

• মূলধন ক্ষমতা এবং লেনদেনের খরচ

প্রতিটি কৌশলের একটি ন্যূনতম এবং সর্বোচ্চ মূলধনের পরিমাণ থাকে, সর্বনিম্ন থ্রেশহোল্ড সাধারণত লেনদেনের খরচ দ্বারা নির্ধারিত হয়।

অত্যধিক স্টক ট্রেড করার ফলে উচ্চ লেনদেন খরচ হবে। ধরে নিচ্ছি আপনি 1,000 শেয়ার কিনতে চান, প্রতিটি পুনঃব্যালেন্সিং এর জন্য কয়েক হাজার ডলার খরচ হবে। আপনার মূলধনের ভিত্তি অবশ্যই যথেষ্ট উচ্চ হতে হবে যাতে লেনদেনের খরচ আপনার কৌশল দ্বারা উত্পন্ন আয়ের একটি ছোট অংশের প্রতিনিধিত্ব করে। উদাহরণস্বরূপ, যদি আপনার মূলধন হয় \(100,000 এবং আপনার কৌশল প্রতি মাসে 1% (\)1000) উপার্জন করে, তবে এই সমস্ত রিটার্ন লেনদেনের খরচ দ্বারা খাওয়া হবে। 1,000 শেয়ারের বেশি লাভের জন্য এই কৌশলটি চালানোর জন্য আপনার মিলিয়ন মিলিয়ন ডলার মূলধন প্রয়োজন।

ন্যূনতম সম্পদ থ্রেশহোল্ড প্রধানত ট্রেড করা শেয়ারের সংখ্যার উপর নির্ভর করে। যাইহোক, সর্বোচ্চ ক্ষমতাও খুব বেশি, এবং দীর্ঘ-সংক্ষিপ্ত ভারসাম্যপূর্ণ ইক্যুইটি কৌশলটি তার প্রান্ত না হারিয়ে কয়েক মিলিয়ন ডলার বাণিজ্য করতে সক্ষম। এটি সত্য কারণ কৌশলটি তুলনামূলকভাবে কদাচিৎ সম্পদের মোট সংখ্যাকে ভাগ করলে শেয়ার প্রতি ডলারের মূল্য খুব কম হবে এবং আপনার ট্রেডিং ভলিউম বাজারকে প্রভাবিত করার বিষয়ে আপনাকে চিন্তা করতে হবে না। ধরা যাক আপনি 1,000 শেয়ার ট্রেড করেন, যা \(100,000,000। আপনি যদি প্রতি মাসে সমগ্র পোর্টফোলিওর ভারসাম্য বজায় রাখেন, তাহলে প্রতিটি স্টক প্রতি মাসে মাত্র \)100,000 লেনদেন করবে, যা বেশিরভাগ সিকিউরিটিজের জন্য একটি উল্লেখযোগ্য মার্কেট শেয়ার হওয়ার জন্য যথেষ্ট নয়।