配对交易是基于数学分析制定交易策略的一个很好的例子.在本文中,我们将演示如何利用数据来创建和自动化配对交易策略。

基本原则

假设你有一对投资标的X和Y具有一些潜在的关联，例如两家公司生产相同的产品，如百事可乐和可口可乐。你希望这两者的价格比率或基差（也称为差价）随时间的变化而保持不变。然而，由于临时供需变化，如一个投资标的的大买/卖订单，对其中一家公司的重要新闻的反应等，这两对之间的价差可能会不时出现分歧。在这种情况下，一只投资标的向上移动而另一只投资标的相对于彼此向下移动。如果你希望这种分歧随着时间的推移恢复正常，你就可以发现交易机会(或套利机会)。此种套利机会在数字货币市场或者国内商品期货市场比比皆是,比如BTC与避险资产的关系;期货中豆粕,豆油与大豆品种之间的关系.

当存在暂时性价格差异时，对交易将卖出表现优异的投资标的（上涨的投资标的）并买入表现不佳的投资标的（下跌的投资标的）.你敢肯定，两只投资标的之间的利差最终会通过表现优异的投资标的回落或表现不佳的投资标的回升或两者兼而有之.你的交易将在所有类似的这些情景中赚钱。如果投资标的一起向上移动或向下移动而不改变它们之间的差价，你就不会赚钱或亏钱。

因此，配对交易是一种市场中性交易策略，使交易者能够从几乎任何市场条件中获利：上升趋势，下降趋势或横向盘整。

解释概念：两个假设的投资标的

• 在发明者量化平台搭建我们的研究环境

首先,为了工作的顺利进行,我们需要搭建我们的研究环境,本文我们使用发明者量化平台(FMZ.COM)进行研究环境的搭建,主要是为了后期可以使用此平台的方便快捷的API接口和封装完善的Docker系统.

在发明者量化平台的官方称呼中，这个Docker系统被称为托管者系统。

关于如何部署托管者和机器人，请参考我之前的文章：https://www.fmz.com/bbs-topic/4140

想购买自己云计算服务器部署托管者的读者，可以参考这篇文章：https://www.fmz.com/bbs-topic/2848

在成功部署好云计算服务与托管者系统后，接下来，我们要安装Python目前最大的神器：Anaconda

为了实现本文所需的所有相关程序环境（依赖库，版本管理等），最简单的办法就是用Anaconda。它是一个打包的Python数据科学生态系统和依赖库管理器。

关于Anaconda的安装方法，请查看Anaconda官方指南：https://www.anaconda.com/distribution/

本文还将用到numpy和pandas这两个目前在Python科学计算方面十分流行且重要的库.

以上这些基础工作也可参考我之前的文章,里面有关于如何设置Anaconda环境和numpy和pandas这两个库的介绍,详情请见: https://www.fmz.com/digest-topic/4169

接下来,让我们用代码实现一个"两个假设的投资标的"

import numpy as np
import pandas as pd

import statsmodels
from statsmodels.tsa.stattools import coint
# just set the seed for the random number generator
np.random.seed(107)

import matplotlib.pyplot as plt

没错,我们还将用到matplotlib这个非常著名的Python中的图表库

让我们生成一个假设的投资标的X，并通过正态分布来模拟绘制它的每日回报。然后我们执行累积和以获得每日的X值。

# Generate daily returns
Xreturns = np.random.normal(0, 1, 100) 
# sum them and shift all the prices up
X = pd.Series(np.cumsum(
    Xreturns), name='X') 
    + 50
X.plot(figsize=(15,7))
plt.show()

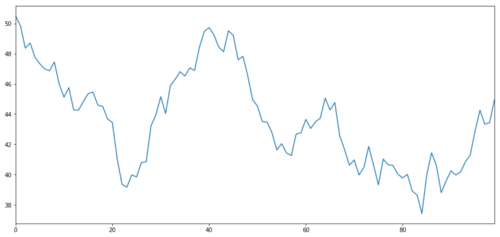
投资标的X，通过正态分布来模拟绘制它的每日回报

现在我们生成的Y与X有很强的相互关联，因此Y的价格应该与X的变化非常相似。我们通过取X，将其向上移动并添加从正态分布中抽取的一些随机噪声对此进行建模。

noise = np.random.normal(0, 1, 100)
Y = X + 5 + noise
Y.name = 'Y'
pd.concat([X, Y], axis=1).plot(figsize=(15,7))
plt.show()

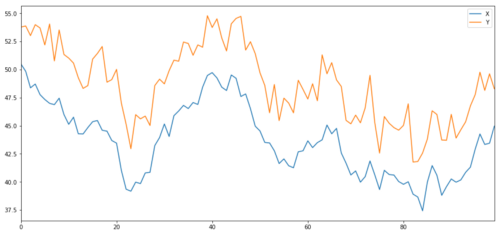
协整投资标的X和Y

协整

协整非常类似于相关性，意味着两个数据系列之间的比率将在平均值附近变化.Y和X这两个系列遵循以下内容：

Y = ⍺ X + e

其中⍺是恒定比率，e是噪声。

对于在两个时间序列之间的交易对，该比率随时间的预期值必定会收敛于均值，即它们应该是协整的。我们上面构建的时间序列是协整的。我们现在将绘制两者之间的比例，以便我们可以看到它的外观。

(Y/X).plot(figsize=(15,7)) 
plt.axhline((Y/X).mean(), color='red', linestyle='--') 
plt.xlabel('Time')
plt.legend(['Price Ratio', 'Mean'])
plt.show()

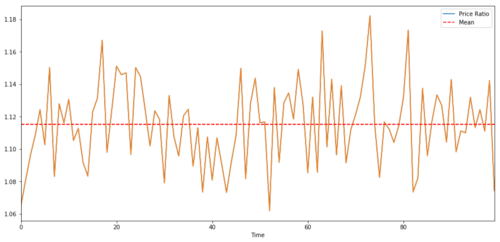
两个协整的投资标的价格之间的比率和平均值

协整测试

有一个方便的测试方法，就是使用statsmodels.tsa.stattools。我们应该会看到一个非常低的p值，因为我们人为地创建了两个尽可能协整的数据系列。

# compute the p-value of the cointegration test
# will inform us as to whether the ratio between the 2 timeseries is stationary
# around its mean
score, pvalue, _ = coint(X,Y)
print pvalue

其结果为: 1.81864477307e-17

注意：相关性与协整性

相关和协整虽然在理论上相似，但并不相同。让我们看看相关但不是协整的数据系列的例子，和反之亦然的例子。首先让我们检查一下我们刚刚生成的系列的相关性。

X.corr(Y)

结果为: 0.951

正如我们所料，这是非常高的。但两个相关但不协整的系列怎么样呢？一个简单的例子就是两个偏离的数据系列。

ret1 = np.random.normal(1, 1, 100)
ret2 = np.random.normal(2, 1, 100)

s1 = pd.Series( np.cumsum(ret1), name='X')
s2 = pd.Series( np.cumsum(ret2), name='Y')

pd.concat([s1, s2], axis=1 ).plot(figsize=(15,7))
plt.show()
print 'Correlation: ' + str(X_diverging.corr(Y_diverging))
score, pvalue, _ = coint(X_diverging,Y_diverging)
print 'Cointegration test p-value: ' + str(pvalue)

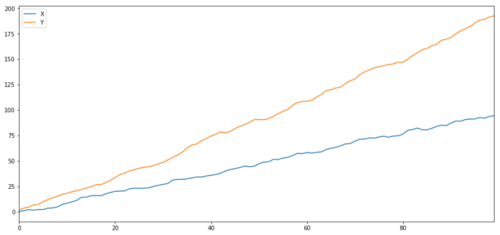
两个相关系列（未共同整合）

相关系数：0.998 协整检验p值：0.258

没有相关性的协整的简单例子是正态分布序列和方波。

Y2 = pd.Series(np.random.normal(0, 1, 800), name='Y2') + 20
Y3 = Y2.copy()

Y3[0:100] = 30
Y3[100:200] = 10
Y3[200:300] = 30
Y3[300:400] = 10
Y3[400:500] = 30
Y3[500:600] = 10
Y3[600:700] = 30
Y3[700:800] = 10
Y2.plot(figsize=(15,7))
Y3.plot()
plt.ylim([0, 40])
plt.show()
# correlation is nearly zero
print 'Correlation: ' + str(Y2.corr(Y3))
score, pvalue, _ = coint(Y2,Y3)
print 'Cointegration test p-value: ' + str(pvalue)

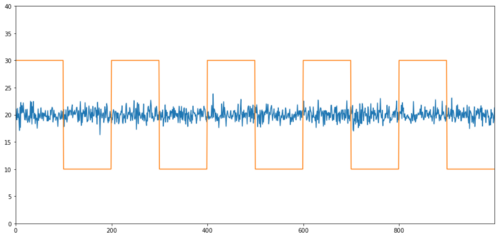
相关性：0.007546 协整检验p值：0.0

相关性非常低，但p值显示出完美的协整性！

如何进行配对交易？

因为两个协整的时间序列（例如上面的X和Y）彼此相向和相互偏离，所以有时会出现基差高和基差低的情况。我们通过购买一个投资标的并卖出另一个投资标的进行配对交易。这样，如果两种投资标的一起下跌或一起上涨，我们既不赚钱也不赔钱,即我们是市场的中立者。

回到上边的Y = ⍺ X + e中的X和Y，使得比率（Y / X）围绕它的平均值⍺移动，我们通过均值回归的比率赚钱.为了做到这一点，我们会注意当X和Y相隔很远的情况，即⍺值太高或太低：

• 做多比率:这是当比率⍺很小并且我们预计它变大时。在上面的例子中，我们通过做多Y并做空X来开仓。

• 做空比率:这是当比率⍺很大并且我们期望它变小时。在上面的例子中，我们通过做空Y和做多X来开仓。

请注意，我们总是有一个“对冲头寸”：如果交易标的买入损失价值，空头头寸会赚钱，反之亦然，因此我们对整体市场走势免疫。

交易标的X和Y相对于彼此移动，我们就会赚钱或亏损。

使用数据查找行为类似的交易标的

这样做的最佳方式是从你怀疑可能是协整的交易标的开始并执行统计测试。如果你对所有交易配对进行统计测试，你将成为多重比较偏差的牺牲品。

多重比较偏差是指在运行众多测试时错误地生成重要p值的机会增加的情况，因为我们需要运行大量测试。如果对随机数据进行100次测试，我们应该会看到5个p值低于0.05。如果你要比较n个交易标的以进行协整，那么你将执行n（n-1）/ 2个比较，你就会看到许多不正确的p值，这会随着你的测试样本的增加而增加。为了避免这种情况，选择少数几个交易配对你有理由确定可能是协整,然后去单独测试他们。这将会大大降低多重比较偏差。

因此，让我们试着找一些表现出协整的交易标的.让我们以标准普尔500指数中一篮子美国大型科技股为例,这些交易标的在相似的细分市场中运作，并且具有协整的价格。我们扫描交易标的清单并测试所有配对之间的协整。

返回的协整检验分数矩阵，p值矩阵以及p值小于0.05的所有配对。这种方法容易出现多重比较偏差，所以实际上他们需要进行二次验证。 在本文中,为了我们的讲解方便,例子中我们选择忽略这一点。

def find_cointegrated_pairs(data):
    n = data.shape[1]
    score_matrix = np.zeros((n, n))
    pvalue_matrix = np.ones((n, n))
    keys = data.keys()
    pairs = []
    for i in range(n):
        for j in range(i+1, n):
            S1 = data[keys[i]]
            S2 = data[keys[j]]
            result = coint(S1, S2)
            score = result[0]
            pvalue = result[1]
            score_matrix[i, j] = score
            pvalue_matrix[i, j] = pvalue
            if pvalue < 0.02:
                pairs.append((keys[i], keys[j]))
    return score_matrix, pvalue_matrix, pairs

注意：我们在数据中包含了市场基准（SPX）- 市场推动了许多交易标的的流动，通常你可能会发现两个看似协整的交易标的; 但实际上它们并没有相互协整，而是与市场协整。这被称为混杂变量.检查你发现的任何关系中的市场参与度是很重要的。

from backtester.dataSource.yahoo_data_source import YahooStockDataSource
from datetime import datetime
startDateStr = '2007/12/01'
endDateStr = '2017/12/01'
cachedFolderName = 'yahooData/'
dataSetId = 'testPairsTrading'
instrumentIds = ['SPY','AAPL','ADBE','SYMC','EBAY','MSFT','QCOM',
                 'HPQ','JNPR','AMD','IBM']
ds = YahooStockDataSource(cachedFolderName=cachedFolderName,
                            dataSetId=dataSetId,
                            instrumentIds=instrumentIds,
                            startDateStr=startDateStr,
                            endDateStr=endDateStr,
                            event='history')
data = ds.getBookDataByFeature()['Adj Close']
data.head(3)

现在让我们尝试使用我们的方法找到协整的交易配对。

# Heatmap to show the p-values of the cointegration test
# between each pair of stocks
scores, pvalues, pairs = find_cointegrated_pairs(data)
import seaborn
m = [0,0.2,0.4,0.6,0.8,1]
seaborn.heatmap(pvalues, xticklabels=instrumentIds, 
                yticklabels=instrumentIds, cmap=’RdYlGn_r’, 
                mask = (pvalues >= 0.98))
plt.show()
print pairs

[('ADBE', 'MSFT')]

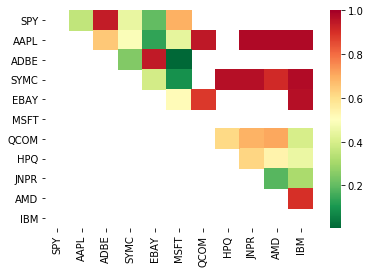
看起来’ADBE’和’MSFT’是协整的。 让我们来看看价格，以确保它真正有意义。

S1 = data['ADBE']
S2 = data['MSFT']
score, pvalue, _ = coint(S1, S2)
print(pvalue)
ratios = S1 / S2
ratios.plot()
plt.axhline(ratios.mean())
plt.legend([' Ratio'])
plt.show()

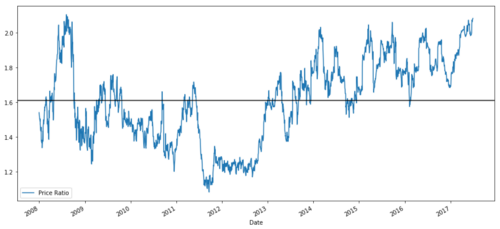
2008 - 2017年MSFT与ADBE之间的价格比率图

这个比率确实看起来像一个稳定的平均值。绝对比率在统计学上并不是很有用。通过将其视为z分数来标准化我们的信号更有帮助。Z分数定义为：

Z Score (Value) = (Value — Mean) / Standard Deviation

警告

实际上，我们通常会尝试对数据进行一些扩展，但前提是这些数据是正态分布的。但是，许多财务数据并非正态分布，所以我们必须非常小心，不要在生成统计数据时简单地假设正态性或任何特定分布。比率的真实分布可能会有肥尾效应，并且那些倾向于极端的数据会使我们的模型变得混乱并导致巨大的损失。

def zscore(series):
    return (series - series.mean()) / np.std(series)

zscore(ratios).plot()
plt.axhline(zscore(ratios).mean())
plt.axhline(1.0, color=’red’)
plt.axhline(-1.0, color=’green’)
plt.show()

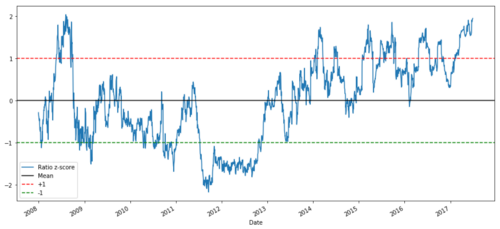
2008 - 2017年间MSFT与ADBE之间的Z价格比率

现在可以更容易的观察比率在均值附近的移动，但有时容易出现与均值的大的差异，我们可以利用这一点。

现在我们已经讨论了配对交易策略的基础知识，并根据历史价格确定了共同整合的交易标的，让我们尝试开发一个交易信号。首先，让我们回顾一下使用数据技术开发交易信号的步骤：

• 收集可靠的数据和清理数据

• 从数据创建功能以识别交易信号/逻辑

• 功能可以是移动平均值或价格数据，相关性或更复杂信号的比率 - 将这些组合起来创建新功能

• 使用这些功能生成交易信号，即哪些信号是买入，卖出或空仓观望

幸运的是,我们有发明者量化平台(fmz.com)为我们完成了上边四个方面的工作,者对于策略开发者来说,是巨大的福音,我们可以把精力和时间都用在策略逻辑的设计上和功能的扩展上.

在发明者量化平台,有封装好的各种主流交易所的接口,我们需要做的只是调用这些API接口,剩下的底层实现逻辑,已经有专业的团队把它打磨好了.

本文为了逻辑的完整和对于原理的解释,这里我们会把这些底层的逻辑进行庖丁解牛般的呈现,但在实际操作中,各位读者可以直接调用发明者量化的API接口来完成以上四方面.

让我们开始:

第一步：设置你的问题

在这里，我们试图创建一个信号，告诉我们在下一个时刻该比率是买入还是卖出，即我们的预测变量Y：

Y = Ratio is buy (1) or sell (-1)

Y(t)= Sign(Ratio(t+1) — Ratio(t))

请注意，我们不需要预测实际交易标的价格，甚至不需要预测比率的实际价值（尽管我们可以），只需要预测下一步的比率方向

第二步：收集可靠和准确的数据

发明者量化是你的朋友！你只需指定要交易的交易标的和要使用的数据源，它就会提取所需的数据并清除它以进行股息和交易标的拆分。所以我们这里的数据已经很干净了。

我们在过去10年（大约2500个数据点）的交易日,通过使用雅虎财经获得的以下数据：开盘价，收盘价，最高价，最低价和交易量

第三步：拆分数据

不要忘记测试模型准确性的这个非常重要的步骤。我们正在使用以下数据的训练/验证/测试拆分

• Training 7 years ~ 70%

• Test ~ 3 years 30%

ratios = data['ADBE'] / data['MSFT']
print(len(ratios))
train = ratios[:1762]
test = ratios[1762:]

理想情况下，我们也应该制作验证集，但我们暂时不会这样做。

第四步：特征工程

相关功能可以是什么？我们想预测比率变动的方向。我们已经看到我们的两个交易标的是协整的，所以这个比率往往会转移并回归到均值。看来我们的特征应该是比率均值的某些度量，当前值与均值的差异能够产生我们的交易信号。

我们使用以下功能：

• 60天移动平均比率：滚动平均值的测量

• 5天移动平均比率：平均值的当前值的测量

• 60天标准差

• z分数：（5d MA - 60d MA）/ 60d SD

ratios_mavg5 = train.rolling(window=5,
                               center=False).mean()
ratios_mavg60 = train.rolling(window=60,
                               center=False).mean()
std_60 = train.rolling(window=60,
                        center=False).std()
zscore_60_5 = (ratios_mavg5 - ratios_mavg60)/std_60
plt.figure(figsize=(15,7))
plt.plot(train.index, train.values)
plt.plot(ratios_mavg5.index, ratios_mavg5.values)
plt.plot(ratios_mavg60.index, ratios_mavg60.values)
plt.legend(['Ratio','5d Ratio MA', '60d Ratio MA'])
plt.ylabel('Ratio')
plt.show()

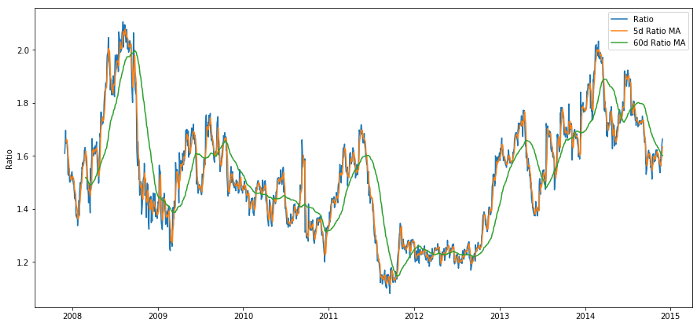
60d和5d MA的价格比率

plt.figure(figsize=(15,7))
zscore_60_5.plot()
plt.axhline(0, color='black')
plt.axhline(1.0, color='red', linestyle='--')
plt.axhline(-1.0, color='green', linestyle='--')
plt.legend(['Rolling Ratio z-Score', 'Mean', '+1', '-1'])
plt.show()

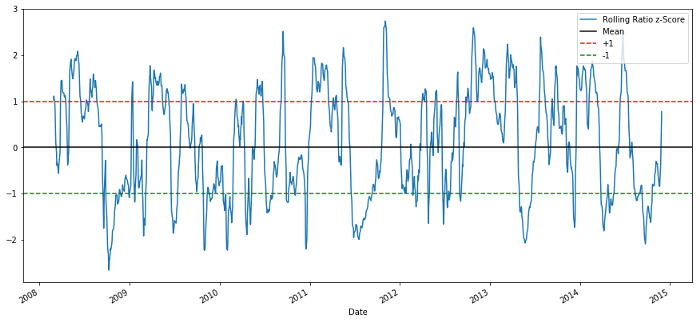
60-5 Z分数价格比例

滚动均值的Z分数确实带出了比率的均值回归性质！

第五步：模型选择

让我们从一个非常简单的模型开始。查看z分数图表，我们可以看到，只要z分数太高或太低，它就会回归。让我们使用+ 1 / -1作为我们的阈值来定义太高和太低，然后我们可以使用以下模型来生成交易信号：

• 当z低于-1.0，比率就是买（1），因为我们预计z会回归到0，因此比率增加

• 当z高于1.0时，比率是卖出（-1），因为我们预计z会回归到0，因此比率降低

第六步：训练，验证和优化

最后，让我们看看我们的模型对实际数据的实际影响？让我们看看这个信号在实际比率上的表现

# Plot the ratios and buy and sell signals from z score
plt.figure(figsize=(15,7))
train[60:].plot()
buy = train.copy()
sell = train.copy()
buy[zscore_60_5>-1] = 0
sell[zscore_60_5<1] = 0
buy[60:].plot(color=’g’, linestyle=’None’, marker=’^’)
sell[60:].plot(color=’r’, linestyle=’None’, marker=’^’)
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,ratios.min(),ratios.max()))
plt.legend([‘Ratio’, ‘Buy Signal’, ‘Sell Signal’])
plt.show()

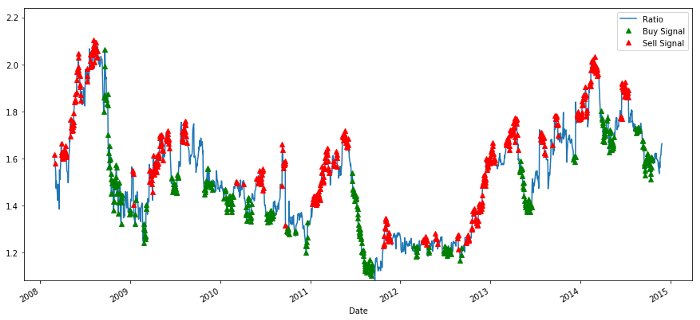
买入和卖出价格比率信号

这个信号似乎是合理的，我们似乎在它高或增加时卖出比率（红点）并在它低（绿点）和减少时买回。这对我们交易的实际交易标的意味着什么？让我们来看看

# Plot the prices and buy and sell signals from z score
plt.figure(figsize=(18,9))
S1 = data['ADBE'].iloc[:1762]
S2 = data['MSFT'].iloc[:1762]
S1[60:].plot(color='b')
S2[60:].plot(color='c')
buyR = 0*S1.copy()
sellR = 0*S1.copy()
# When buying the ratio, buy S1 and sell S2
buyR[buy!=0] = S1[buy!=0]
sellR[buy!=0] = S2[buy!=0]
# When selling the ratio, sell S1 and buy S2 
buyR[sell!=0] = S2[sell!=0]
sellR[sell!=0] = S1[sell!=0]
buyR[60:].plot(color='g', linestyle='None', marker='^')
sellR[60:].plot(color='r', linestyle='None', marker='^')
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,min(S1.min(),S2.min()),max(S1.max(),S2.max())))
plt.legend(['ADBE','MSFT', 'Buy Signal', 'Sell Signal'])
plt.show()

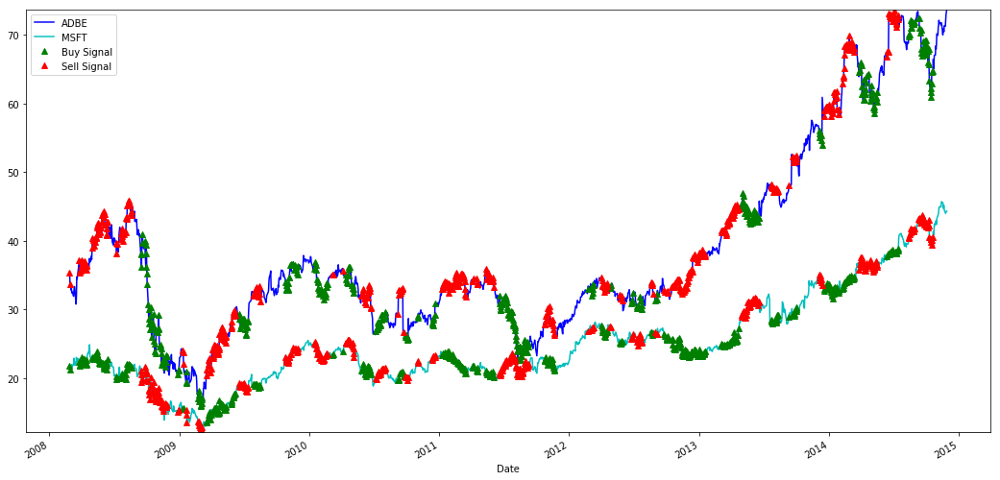
购买和出售MSFT和ADBE股票的信号

请注意我们有时如何在"短腿"上赚钱，有时在"长腿"上赚钱，有时两者兼而有之。

我们对训练数据的信号感到满意。让我们看看这个信号可以产生什么样的利润。当比率较低时，我们可以制作一个简单的回测器，买入1个比率（买入1 ADBE股票和卖出比率x MSFT股票），当它高时卖出1个比率（卖出1个ADBE股票和买入比率x MSFT股票）并计算这些比率的PnL交易。

# Trade using a simple strategy
def trade(S1, S2, window1, window2):
    
    # If window length is 0, algorithm doesn't make sense, so exit
    if (window1 == 0) or (window2 == 0):
        return 0
    
    # Compute rolling mean and rolling standard deviation
    ratios = S1/S2
    ma1 = ratios.rolling(window=window1,
                               center=False).mean()
    ma2 = ratios.rolling(window=window2,
                               center=False).mean()
    std = ratios.rolling(window=window2,
                        center=False).std()
    zscore = (ma1 - ma2)/std
    
    # Simulate trading
    # Start with no money and no positions
    money = 0
    countS1 = 0
    countS2 = 0
    for i in range(len(ratios)):
        # Sell short if the z-score is > 1
        if zscore[i] > 1:
            money += S1[i] - S2[i] * ratios[i]
            countS1 -= 1
            countS2 += ratios[i]
            print('Selling Ratio %s %s %s %s'%(money, ratios[i], countS1,countS2))
        # Buy long if the z-score is < 1
        elif zscore[i] < -1:
            money -= S1[i] - S2[i] * ratios[i]
            countS1 += 1
            countS2 -= ratios[i]
            print('Buying Ratio %s %s %s %s'%(money,ratios[i], countS1,countS2))
        # Clear positions if the z-score between -.5 and .5
        elif abs(zscore[i]) < 0.75:
            money += S1[i] * countS1 + S2[i] * countS2
            countS1 = 0
            countS2 = 0
            print('Exit pos %s %s %s %s'%(money,ratios[i], countS1,countS2))
            
            
    return money
trade(data['ADBE'].iloc[:1763], data['MSFT'].iloc[:1763], 60, 5)

结果为: 1783.375

所以这个策略似乎有利可图的！现在，我们可以通过更改移动平均时间窗口，通过更改买入/卖出和平仓的阈值等进一步优化，并检查验证数据的性能改进。

我们还可以尝试更复杂的模型，如Logistic回归，SVM等，以进行1 / -1预测。

现在，让我们推进这个模型，这将我们带到

第七步：对测试数据进行回测

这里再提一下发明者量化平台,它使用高性能的QPS/TPS回测引擎，真实的重现历史环境，消除常见的量化回测陷阱，及时发现策略的不足，从而更好的为实盘投资提供帮助。

本文为了解释原理,还是选择把底层逻辑展示出来,在实际运用中,还是推荐各位读者使用发明者量化平台,除了时间上的节省,重要的是提高容错率.

回测很简单，我们可以使用上面的函数来查看测试数据的PnL

trade(data[‘ADBE’].iloc[1762:], data[‘MSFT’].iloc[1762:], 60, 5)

其结果为: 5262.868

该模型做得很好！它成为了我们第一个简单的配对对交易模型。

避免过度拟合

在结束讨论之前，我想特别讨论一下过度拟合。过度拟合是交易策略中最危险的陷阱。过度拟合算法可能在回测中表现非常出色但在新的看不见的数据上失败 - 这意味着它没有真正揭示数据的任何趋势并且没有真正的预测能力。我们举一个简单的例子。

在我们的模型中，我们使用滚动参数预估并且希望由其优化时间窗口长度。我们可能决定简单地迭代所有可能性，合理的时间窗口长度，并根据我们的模型表现最佳来选择时间长度。下面我们编写一个简单的循环来根据训练数据的pnl对时间窗口长度进行评分并找到最佳的循环。

# Find the window length 0-254 
# that gives the highest returns using this strategy
length_scores = [trade(data['ADBE'].iloc[:1762], 
                data['MSFT'].iloc[:1762], l, 5) 
                for l in range(255)]
best_length = np.argmax(length_scores)
print ('Best window length:', best_length)

('Best window length:', 40)

现在我们检查模型在测试数据上的性能，我们发现这个时间窗口长度远非最佳！这是因为我们原来的选择明显过度拟合了样本数据。

# Find the returns for test data
# using what we think is the best window length
length_scores2 = [trade(data['ADBE'].iloc[1762:], 
                  data['MSFT'].iloc[1762:],l,5) 
                  for l in range(255)]
print (best_length, 'day window:', length_scores2[best_length])
# Find the best window length based on this dataset, 
# and the returns using this window length
best_length2 = np.argmax(length_scores2)
print (best_length2, 'day window:', length_scores2[best_length2])

(40, 'day window:', 1252233.1395)
(15, 'day window:', 1449116.4522)

显然适合我们的样本数据并不总能在将来产生良好的结果。只是为了测试，让我们绘制从两个数据集计算的长度分数

plt.figure(figsize=(15,7))
plt.plot(length_scores)
plt.plot(length_scores2)
plt.xlabel('Window length')
plt.ylabel('Score')
plt.legend(['Training', 'Test'])
plt.show()

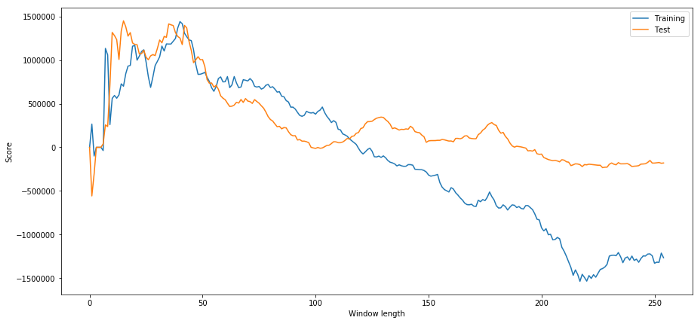
我们可以看到20-50之间的任何东西都是时间窗户的好的选择项。

为了避免过度拟合，我们可以使用经济推理或算法的性质来选择时间窗口长度。我们也可以使用卡尔曼滤波器，它不需要我们指定长度; 稍后将在另一个文章中介绍此方法。

下一步

在这篇文章中，我们提出了一些简单的介绍方法来演示开发交易策略的过程。在实践中，应该使用更复杂的统计数据，大家可以考虑下边的这些选项:

• 赫斯特指数

• 从Ornstein-Uhlenbeck过程推断的均值回归的半衰期

• 卡尔曼滤波器

Related

More