Sieben Regressionstechniken, die Sie beherrschen sollten

**Dieser Artikel erklärt die Regressionsanalyse und ihre Vorteile, wobei die sieben am häufigsten verwendeten Regressionstechniken und ihre Schlüsselfaktoren, wie z. B. lineare Regression, logische Regression, polymorphe Regression, schrittweise Regression, Kettenregression, Schraubenregression, ElasticNet Regression, und schließlich die Schlüsselfaktoren für die Wahl des richtigen Regressionsmodells, zusammengefasst werden. ** ** Die Regressionsanalyse ist ein wichtiges Werkzeug für die Modellierung und Analyse von Daten. In diesem Artikel werden die Bedeutung und die Vorteile der Regressionsanalyse erläutert, wobei die sieben am häufigsten verwendeten Regressionstechniken und ihre Schlüsselfaktoren, wie z. B. lineare Regression, logische Regression, polymorphe Regression, Schritt-zu-Schritt-Regression, Stachel-Regression, Schnüren-Regression, ElasticNet-Regression, und die Schlüsselfaktoren für die Auswahl des richtigen Regressionsmodells, zusammengefasst werden.**

• ### Was ist Regressionsanalyse?

Regressionsanalyse ist eine Methode zur Vorhersage-Modellierung, die die Beziehung zwischen der Einflussvariable (Ziel) und der Selbstvariable (Vorhersager) untersucht. Diese Methode wird häufig in der Vorhersage-Analyse, im Zeitreihenmodell und in der Kausalbeziehung zwischen den entdeckten Variablen eingesetzt. Zum Beispiel ist die Beziehung zwischen fahrlässigem Fahren und der Anzahl der Straßenverkehrsunfälle am besten durch Regression untersucht.

Regressionsanalyse ist ein wichtiges Werkzeug für die Modellierung und Analyse von Daten. Hier benutzen wir Kurven/Linien, um diese Datenpunkte zusammenzufügen, so dass die Abstandsunterschiede zwischen Kurven oder Linien und Datenpunkten minimal sind.

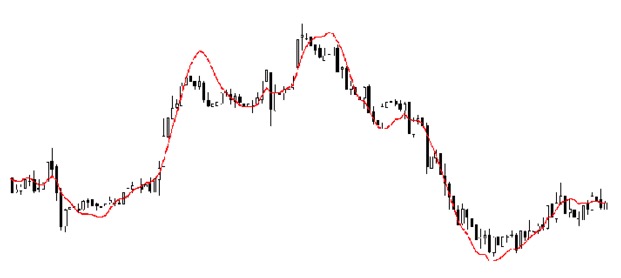
• ### Warum verwenden wir Regressionsanalyse?

Regressionsanalyse schätzt die Beziehung zwischen zwei oder mehreren Variablen, wie bereits erwähnt. Lassen Sie uns ein einfaches Beispiel anführen, um dies zu verstehen:

Zum Beispiel, wenn man unter den aktuellen wirtschaftlichen Bedingungen die Umsatzsteigerung eines Unternehmens schätzen möchte. Jetzt, wo man die neuesten Daten des Unternehmens hat, die zeigen, dass die Umsatzsteigerung etwa 2,5 mal so hoch ist wie die Wirtschaftswachstum. Mit Hilfe der Regressionsanalyse können wir die zukünftigen Umsätze des Unternehmens anhand von aktuellen und vergangenen Informationen prognostizieren.

Regressionsanalysen haben viele Vorteile:

Es zeigt eine signifikante Beziehung zwischen eigen- und resultierenden Variablen.

Es zeigt die Stärke des Einflusses mehrerer Eigenvariablen auf eine Faktorvariable.

Regressionsanalysen ermöglichen es uns auch, die Wechselwirkungen zwischen Variablen zu vergleichen, die auf verschiedenen Maßstäben gemessen werden, wie z. B. die Verbindung zwischen Preisänderungen und der Anzahl der Werbeaktionen. Diese helfen Marktforschern, Datenanalytikern und Datenwissenschaftlern, die beste Gruppe von Variablen auszuschließen und zu schätzen, um ein Prognose-Modell zu erstellen.

• ### Wie viele Regressionstechnologien haben wir?

Es gibt eine Vielzahl von Regressionstechniken, die zur Vorhersage eingesetzt werden können. Diese Techniken haben drei Hauptmerkmale: die Anzahl der Eigenvariablen, die Art der Eigenvariablen und die Form der Regressionslinie. Wir werden sie im folgenden Abschnitt detailliert diskutieren.

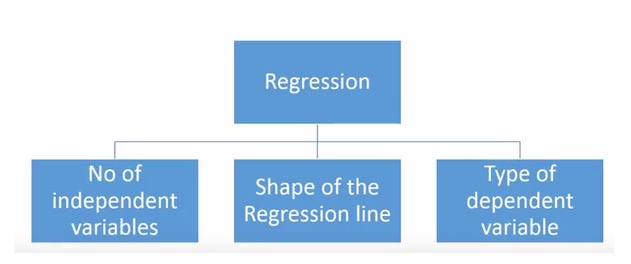
Für diejenigen, die kreativ sind, können Sie sogar ein Regressionsmodell erstellen, das noch nicht verwendet wurde, wenn Sie eine Kombination der obigen Parameter für notwendig halten. Aber bevor Sie anfangen, sollten Sie sich mit den am häufigsten verwendeten Regressionsmethoden vertraut machen:

• 1. Lineare Regression

  Es ist eine der bekanntesten Modellierungstechniken. Die Lineare Regression ist in der Regel eine der Techniken, die man am besten auswählt, um ein Vorhersage-Modell zu erlernen. In dieser Technik ist die Regressionslinie linear, da die Variablen kontinuierlich sind, die Eigenvariablen kontinuierlich oder getrennt sind.

  Die lineare Regression verwendet die optimale Anpassung der Geraden ((d. h. der Regressionslinie), um eine Beziehung zwischen der Faktorvariablen ((Y) und einer oder mehreren Eigenvariablen ((X)) herzustellen.

  Das ist die Gleichung Y = a + b.*X + e, wobei a die Schnittstelle, b die Steigung der Geraden und e der Fehlerpunkt ist. Diese Gleichung kann die Werte der Zielvariablen anhand einer gegebenen Prognosevariablen (s) prognostizieren.

  

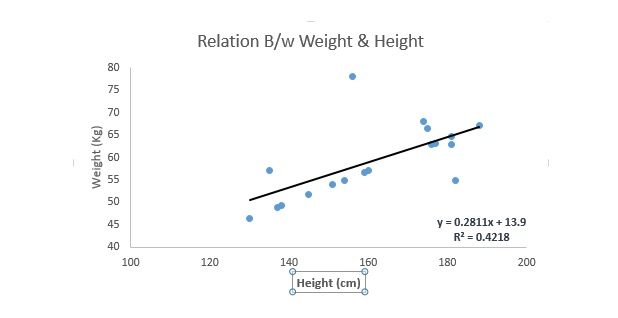
  Der Unterschied zwischen monolinealem Regression und multilinealem Regression besteht darin, dass eine multilineale Regression ((>1) eigenvariablen hat, während eine monolineale Regression normalerweise nur 1 eigenvariablen hat. Die Frage ist nun, wie wir eine optimale Anpassung erhalten.

  Wie erhalte ich die Werte der BEST-FIT-LINE (a und b)?

  Die Problematik lässt sich leicht mit der Minimum-Doppel-Methode lösen. Die Minimum-Doppel-Methode ist auch die am häufigsten verwendete Methode, um eine regressive Linie zu ermitteln. Für die Beobachtungsdaten berechnet sie die optimale Anpassung durch Minimierung der Summe der vertikalen Abweichungen von jedem Datenpunkt zur Linie. Da bei der Addition die Abweichungen vor dem Quadrat liegen, werden positive und negative Werte nicht kompensiert.

  

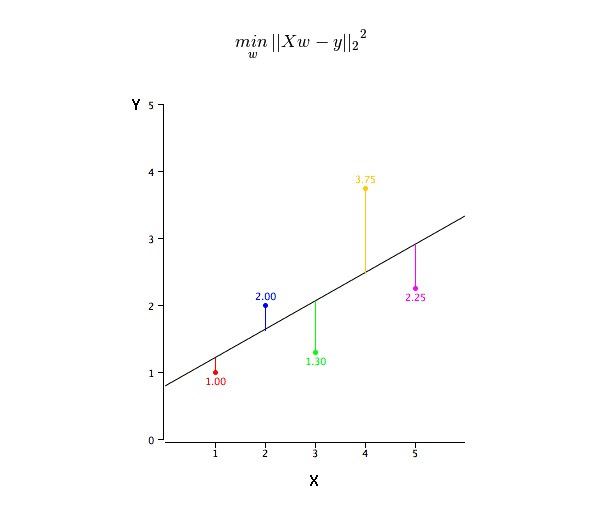
  Wir können die R-square-Indikatoren verwenden, um die Modellleistung zu bewerten. Für weitere Informationen zu diesen Indikatoren lesen Sie Modellleistungskennzahlen Part 1, Part 2.

  Das ist wichtig.

  • Es muss eine lineare Beziehung zwischen Eigenvariablen und Faktorvariablen geben.
  • Die Multivariate-Rückführung hat mehrere Komorne, Korrelation und Divergenz.
  • Die lineare Regression ist sehr empfindlich gegenüber Ausnahmewerten. Sie beeinflusst die Regressionslinie stark und beeinflusst schließlich die Prognosewerte.
  • Die Mehrfach-Kompositivität erhöht die Differenz zwischen den Koeffizienten-Schätzwerten, so dass die Schätzungen bei geringfügigen Änderungen des Modells sehr sensibel sind. Die Folge ist, dass die Koeffizienten-Schätzwerte instabil sind.
  • Bei mehreren eigenvariablen können wir die wichtigsten eigenvariablen mit der vorwärtswahl, der rückwärtswahl und der schrittweisen filterung auswählen.

• 2. Logistic Regression Logische Regression

  Die logische Regression wird verwendet, um die Wahrscheinlichkeit zu berechnen, dass ein Ereignis = Erfolg und ein Ereignis = Misserfolg ist. Wir sollten die logische Regression verwenden, wenn der Typ der berechtigten Variablen eine binäre Variable ist (z. B. 1 / 0, wahr/falsch, ja/nein).

  odds= p/ (1-p) = probability of event occurrence / probability of not event occurrence
  ln(odds) = ln(p/(1-p))
  logit(p) = ln(p/(1-p)) = b0+b1X1+b2X2+b3X3....+bkXk
  

  In den Formeln, die ich oben erwähnt habe, ist p die Wahrscheinlichkeit, dass es ein bestimmtes Merkmal hat. Sie sollten sich fragen: Warum benutzen wir logarithmische Zahlen in der Formel?

  Da wir hier mit einer binären Verteilung ((due Variablen)) arbeiten, müssen wir eine Verbindungsfunktion auswählen, die für diese Verteilung optimal ist. Sie ist die Logit-Funktion. In der obigen Gleichung werden die Parameter durch die Beobachtung der höchsten Wahrscheinlichkeitsschätzung der Stichprobe ausgewählt, anstatt die Quadratur und den Fehler zu minimieren (wie in der Normalregression).

  

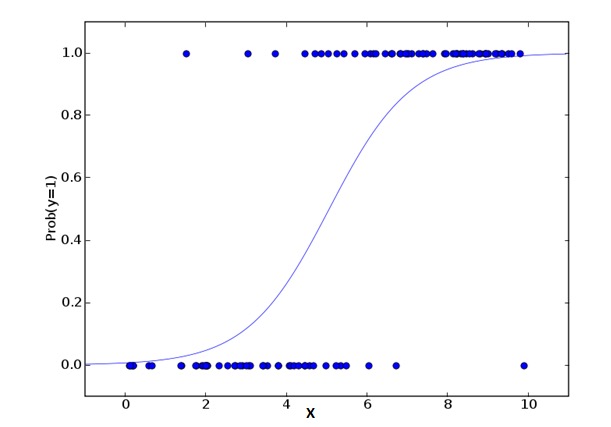
  Das ist wichtig.

  • Es wird häufig für Klassifizierungsfragen verwendet.
  • Die logische Regression verlangt nicht, dass die Eigenvariablen und die Faktorvariablen in einer linearen Beziehung stehen. Sie kann verschiedene Arten von Beziehungen behandeln, da sie eine nichtlineare Log-Konvertierung für den prognostizierten Relativ-Risiko-Index OR verwendet.
  • Um Überpassung und Nichtpassung zu vermeiden, sollten wir alle wichtigen Variablen einbeziehen. Es gibt eine gute Methode, um dies sicherzustellen, und zwar die Schritt-für-Schritt-Filtermethode zur Schätzung der logischen Regression.
  • Es erfordert eine große Anzahl von Stichproben, da bei einer geringen Anzahl von Stichproben die höchsten Wahrscheinlichkeitsschätzungen schlechter sind als bei einer gewöhnlichen Minimum-Doppelzahl.
  • Selbstvariablen sollten nicht miteinander in Beziehung stehen, d.h. nicht mehrfach kohärent sein. In der Analyse und Modellierung können wir jedoch die Auswirkungen der Wechselwirkungen der klassifizierten Variablen einbeziehen.
  • Wenn der Wert der Einflussvariable eine Ordnungsvariable ist, wird sie als Ordnungslogik-Rückkehr bezeichnet.
  • Wenn die Abhängigkeitsvariablen mehrere Klassen haben, wird dies als mehrere logische Regression bezeichnet.

• 3. Polynomialregression

  Für eine Regressionsgleichung ist sie eine polynomiale Regressionsgleichung, wenn der Index der Eigenvariablen größer als 1 ist. Die Gleichung ist wie folgt:

  y=a+b*x^2
  

  In dieser Regressionstechnik ist die optimale Anpassung nicht eine gerade Linie, sondern eine Kurve, die zur Anpassung von Datenpunkten verwendet wird.

  

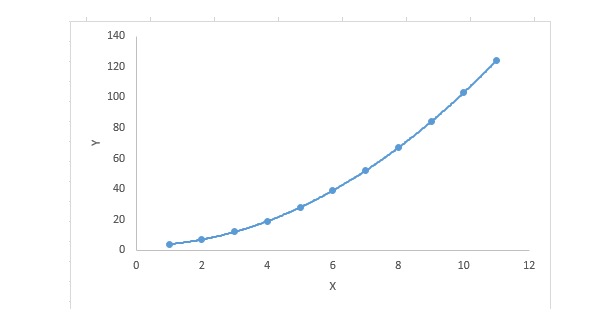
  Schwerpunkte:

  • Obwohl es eine Induktion gibt, die eine hohe Polynomialformel zusammenfügt und einen niedrigeren Fehler erzielt, kann dies zu einer Überübung führen. Sie müssen regelmäßig Beziehungsdiagramme erstellen, um die Übereinstimmung zu überprüfen, und sich darauf konzentrieren, dass die Übereinstimmung vernünftig ist, ohne Überübung oder Fehlübung. Hier ist ein Diagramm, das hilft zu verstehen:

  

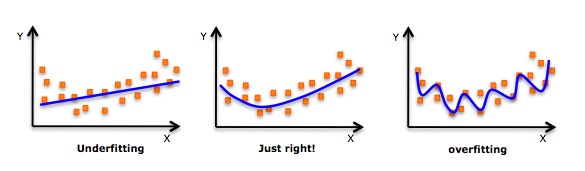
  • Es ist offensichtlich, dass man an beiden Enden der Kurve nach Punkten sucht, um zu sehen, ob diese Formen und Trends sinnvoll sind. Höhere Polynomialzahlen können schließlich zu seltsamen Schlussfolgerungen führen.

• 4. Schrittweise Regression

  Bei der Behandlung von mehreren eigenvarianten können wir diese Form der Regression verwenden. In dieser Technik wird die Auswahl der eigenvarianten in einem automatischen Prozess durchgeführt, der auch nicht-menschliche Handlungen umfasst.

  Diese Leistung besteht darin, wichtige Variablen zu identifizieren, indem man statistische Werte wie R-Quadrat, t-Statistik und AIC-Werte beobachtet. Die Schrittweise Regression wird durch gleichzeitige Hinzufügung/Entfernung von ko-variablen auf Basis von spezifizierten Kriterien angepasst.

  • Die Standard-Schritt-Rückgang-Theorie macht zwei Dinge: Sie erhöht und verringert die Prognosen, die für jeden Schritt benötigt werden.
  • Die Forward-Selection-Methode beginnt mit der wichtigsten Vorhersage im Modell und fügt dann für jeden Schritt eine Variable hinzu.
  • Die rückwärtsgeführte Entfernung beginnt gleichzeitig mit allen Vorhersagen des Modells und beseitigt dann bei jedem Schritt die am wenigsten signifikanten Variablen.
  • Diese Modellierungstechnik zielt darauf ab, die Vorhersagekapazität mit der geringsten Anzahl an Vorhersagevariablen zu maximieren. Es ist eine Methode, um hochdimensionalen Datensätzen zu begegnen.

• 5. Ridge Regression

  Bei der analytischen Regression ist die Standard-Ergebnis-Verringerung möglich, indem die Standard-Ergebnis-Schätzung mit einer zusätzlichen Abweichung erweitert wird.

  Wir haben oben die lineare Regressionsgleichung gesehen.

  y=a+ b*x
  

  Diese Gleichung hat auch einen Fehlerpunkt. Die vollständige Gleichung ist:

  y=a+b*x+e (error term),  [error term is the value needed to correct for a prediction error between the observed and predicted value]
  => y=a+y= a+ b1x1+ b2x2+....+e, for multiple independent variables.
  

  In einer linearen Gleichung kann der Prognosefehler in zwei Subpartien aufgeteilt werden. Der eine ist die Abweichung, der andere die Differenz. Der Prognosefehler kann durch diese beiden Partien oder durch eine der beiden verursacht werden. Hier werden die Fehler, die durch die Differenz verursacht werden, diskutiert.

  Die Lithium-Rückkehr löst die Problematik der Mehrfachkomorbidität durch die Schrumpfparameter λ ((lambda)). Siehe folgende Formel

  

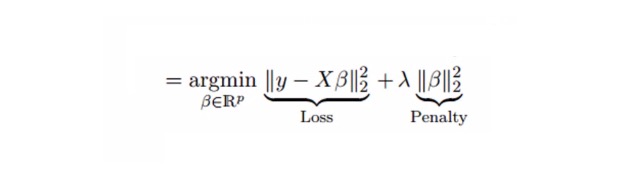
  In dieser Formel gibt es zwei Komponenten. Die erste ist das Minimum-Doppel, die andere ist die λ-Mehrzahl von β2 ((β-quadrat), wobei β der entsprechende Koeffizient ist. Um die Parameter zu verkleinern, wird sie in die Minimum-Doppel hinzugefügt, um eine sehr geringe Differenz zu erhalten.

  Das ist wichtig.

  • Abgesehen von den Konstanten ist diese Regression ähnlich wie bei der Regression zum Minimalpolynomen.
  • Es hat die Werte der relevanten Koeffizienten geschrumpft, aber nicht auf Null, was darauf hindeutet, dass es keine Feature-Selection-Funktion hat
  • Dies ist eine Regulierungsmethode und verwendet die L2-Regulierung.

• 6. Lasso-Regression

  Es ist ähnlich wie die Luminor-Rückführung, wobei der Lasso (Least Absolute Shrinkage and Selection Operator) auch die absolute Größe des Rückgangskoeffizienten verurteilt. Darüber hinaus kann es den Grad der Veränderung reduzieren und die Genauigkeit des linearen Regressionsmodells verbessern. Siehe folgende Formel:

  

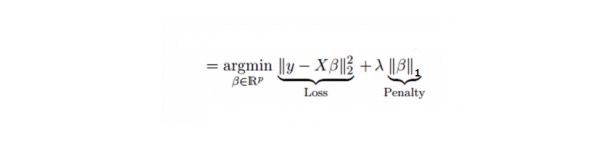
  Die Lasso-Regression unterscheidet sich etwas von der Ridge-Regression darin, dass sie die Strafen als absolute Werte anstelle von Quadraten verwendet. Dies führt dazu, dass die Strafen (oder die Summe der absoluten Werte der Einschätzung der Einschränkung) einige Parameterschätzungen gleich Null ergeben. Je größer die Strafen sind, desto näher kommt die Schätzung an Null.

  Das ist wichtig.

  • Abgesehen von den Konstanten ist diese Regression ähnlich wie bei der Regression zum Minimalpolynomen.
  • Es hat einen Schrumpfkoeffizienten, der nahe bei Null liegt (<= 0), was der Merkmalewahl wirklich hilft.
  • Das ist eine Regulierungsmethode, die die L1-Regulierung verwendet.
  • Wenn eine Gruppe von Variablen in der Vorhersage hochrelevant ist, wählt Lasso eine davon aus und reduziert die anderen auf Null.

• 7. Die Rückkehr des ElasticNet

  ElasticNet ist eine Mischung aus Lasso- und Ridge-Regressionstechniken. Es verwendet L1 zum Trainieren und L2 als Prioritätsregularisierungsmatrix. ElasticNet ist nützlich, wenn mehrere zugehörige Merkmale vorhanden sind. Lasso wählt zufällig eines von ihnen aus, während ElasticNet zwei wählt.

  

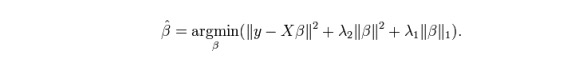
  Der praktische Vorteil zwischen Lasso und Ridge ist, dass es ElasticNet erlaubt, etwas von der Stabilität von Ridge im Kreislaufzustand zu übernehmen.

  Das ist wichtig.

  • In Fällen von stark korrelierten Variablen entsteht ein Cluster-Effekt.
  • Es gibt keine Begrenzung für die Anzahl der zu wählenden Variablen.
  • Es kann doppelte Schrumpfung ertragen.
  • Zusätzlich zu den sieben am häufigsten verwendeten Regressionstechniken können Sie sich auch andere Modelle ansehen, wie Bayesian, Ecological und Robust Regression.

• Wie wählt man das richtige Regressionsmodell?

  Das Leben ist oft einfacher, wenn man nur ein oder zwei Techniken kennt. Eine Ausbildungseinrichtung, die ich kenne, hat ihren Studenten gesagt, dass sie lineare Regression verwenden sollten, wenn die Ergebnisse sequentiell sind. Wenn sie binär sind, verwenden sie logische Regression.

  Bei einem Multivariate-Regressionsmodell ist es wichtig, die am besten geeignete Technik zu wählen, basierend auf den Typen der Eigen- und Faktorvariablen, den Dimensionen der Daten und anderen grundlegenden Eigenschaften der Daten. Die folgenden Faktoren sind entscheidend für die Wahl des richtigen Regressionsmodells:

  Die Erforschung von Daten ist ein notwendiger Bestandteil des Aufbaus von Prognose-Modellen. Sie sollte der erste Schritt sein, um ein geeignetes Modell zu wählen, z. B. um die Beziehungen und Auswirkungen von Variablen zu identifizieren.

  Vergleiche sind besser geeignet für die Vorteile verschiedener Modelle, wir können verschiedene Indikatorparameter analysieren, wie Parameter für die statistische Bedeutung, R-square, Adjusted R-square, AIC, BIC und Fehlerpunkte. Eine andere ist Mallows’ Cp-Richtlinie. Dies geschieht hauptsächlich durch den Vergleich des Modells mit allen möglichen Untermodellen (oder die sorgfältige Auswahl von ihnen), um die möglichen Abweichungen in Ihrem Modell zu überprüfen.

  Die beste Methode, um ein Vorhersage-Modell zu bewerten, ist die Kreuzprüfung. Hier teilen Sie Ihren Datensatz in zwei Teile (eine für das Training und eine für die Verifizierung). Messen Sie die Genauigkeit Ihrer Vorhersage anhand einer einfachen Gleichung zwischen den Beobachtungswerten und den Vorhersagewerten.

  Wenn Ihr Datensatz aus mehreren gemischten Variablen besteht, sollten Sie nicht die Methode der automatischen Modellwahl wählen, da Sie nicht alle Variablen gleichzeitig in das gleiche Modell bringen möchten.

  Es hängt auch von Ihrem Ziel ab. Es kann vorkommen, dass ein weniger robustes Modell einfacher zu realisieren ist als ein Modell mit hoher statistischer Bedeutung.

  Die Regression-Regularisierungsmethoden ((Lasso, Ridge und ElasticNet) funktionieren gut unter mehrfacher Kollinarität zwischen hochdimensionalen und Datensatzvariablen.

Übertragen von CSDN